基于流固热耦合的压气机离心叶轮结构变形优化

杨雨晨 金海良 陈璇

(中国航发湖南动力机械研究所，湖南中小型航空发动机叶轮机械重点实验室，湖南株洲 412002)

对于航空发动机压气机结构，往往需要尽可能地减小其静子流道与转子叶尖的间隙，这不仅仅是为了减少气动泄露提高效率的需要，也成为设计与实际匹配的关键影响参数[1]。但随着离心叶轮的设计向着切线速度更高压比更大的方向发展，离心叶轮所受流道内气动载荷与离心力载荷也越来越大，在叶轮材料给定的基础上，离心叶轮的变形也更大，一旦工作中有转静子碰磨，很容易造成安全事故。因此，发展一种压气机离心叶轮结构变形优化方法具有重要的工程应用价值。

针对离心叶轮结构优化，目前国内的研究重点在对应力分布的优化。蔡显新等[2]运用改进的耦合分析数学模型对叶轮应力分布进行了优化。李可可[3]用自行开发的多学科设计优化软件对离心叶轮轮盘进行了形状优化设计，降低了轮盘的最高应力，减轻了重量。陈鼎新等[4]以结构质量与结构应力指标为优化目标，提出一种基于代理模型―遗传算法的离心叶轮结构设计参数全面优化方法。在实际工作中，叶轮的变形对于压气机性能、工作安全的影响也较大。

本文基于ANSYS-Workbench平台，针对压气机离心叶轮的结构特征，提出一种基于流固热耦合的压气机离心结构叶轮变形优化方法。将参数化的离心叶轮在耦合信息传递的基础上依次开展气动、强度、变形分析；基于拉丁超立方试验设计获得影响结构变形的主要因素，选取关键结构尺寸作为主要优化设计变量，以变形为目标，采用Kriging代理模型和NSGA-Ⅱ多目标优化算法开展离心叶轮的多学科优化设计；通过对比优化前后离心叶轮结构变形量，验证结构优化设计的有效性。

1.参数化建模与流固热耦合数值分析

如图1所示利用UG建立离心叶轮参数化模型，对离心叶轮进行流固热耦合分析。首先采用CFX进行离心叶轮三维流动特性分析。计算网格采用ANSYS17.2的TurboGrid模块生成，采用六面体结构化网格，网格数为177432；选用K-ε湍流模型；边界条件取设计点工作情况下的进口总温、总压，出口取平均静压。计算得到流场，根据外掠平板对流换热模型得到温度场。

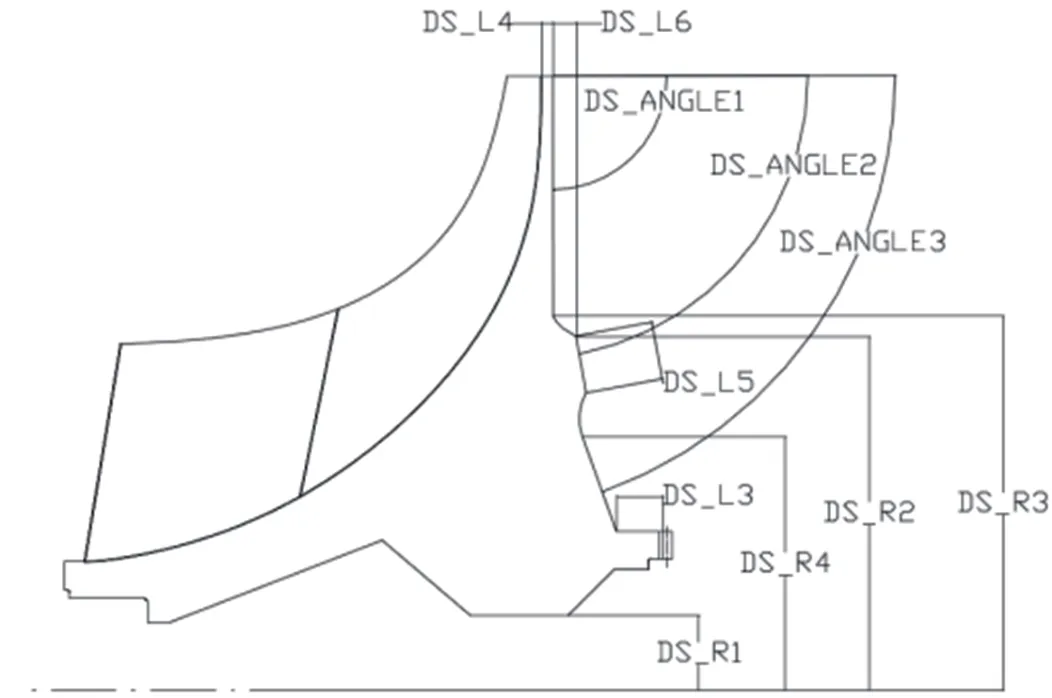
图1 离心叶轮参数化示意图

使用Workbench对TC11钛合金离心叶轮特征块的结构强度分析。利用插值方法将流场分析得到的温度、气压传递至结构分析模型；采用10节点四面体单元进行网格划分，施加循环周期性边界条件、转速等，进行变形、强度分析，并输出质量和关键区域的应力、应变等信息，计算得到原始模型的质量为0.31kg、轮芯应力为685.0193MPa、最大总变形为0.54657mm。

2.优化方法

2.1 优化方案及流程

本文通过控制离心叶轮出口轮背的总变形量，将轮芯应力、总质量设为约束条件，从而将多目标优化问题表示为如下数学模型[5]：

设计变量：X={x1，x2…xn}T

目标函数：Min[f(X)]=H

约束条件：Xs≤X≤Xt，vi(X)≤0(i=1，2…k)，式中：X为设计变量，离心叶轮变形H为目标函数，Xs、Xt分别为设计变量的上、下限，vi(X)为约束函数。

将该方法应用于压气机离心叶轮的优化设计中，能够使设计者在短时间内分析比较大量设计方案，预先淘汰绝大多数非优方案，一步步逼近多学科整体最优解，从而有效的提高设计质量，缩短优化设计周期，其具体流程如图2所示，具体过程如下：

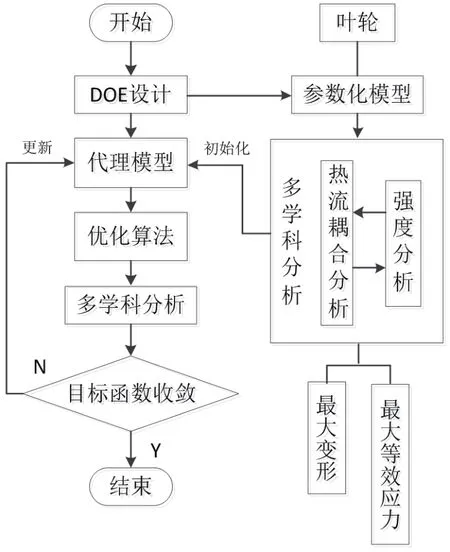
图2 结构变形优化流程图

（1）确定优化设计变量；根据其设计要求、设计准则，确定优化设计的目标和约束。

（2）在离心叶轮多学科分析基础上，在设计空间中进行试验设计，确定关键设计变量、以及设计变量变化范围等。

（3）利用DOE分析获得的有效样本点，建立优化设计变量与离心叶轮多学科分析结果间的代理模型，通过误差分析保证代理模型的精度。

（4）在Kriging代理模型的基础上，利用多目标遗传优化算法对离心叶轮性能和变形参数进行多学科优化并确定最优方案，优化过程中更新代理模型保证优化设计的精度。

2.2 试验设计

试验设计方法是有关如何合理安排试验的数学方法，决定了构造代理模型所需样本点的个数及样本点的空间分布情况，优良的试验设计方法应保证试验次数尽可能少且所选样本尽可能充满整个试验空间。本文在试验设计方面采用目前最为常用的拉丁超立方设计方法（Latin Hypercube Design，LHD），目前已经获得了广泛的应用[6]。

拉丁超立方试验方法的基本原理及详细数学公式见文献[6]。图3～图4中给出了将该方法运用于二维及三维空间取样的效果示意图[7]，可以看出它具有高效的对样本空间进行填充，极大地避免了重复样本的选取，理论上能够显著减小采样次数[8]。本文使用Workbench优化模块的DOE，共得到300个样本点，其中有效样本点191个。

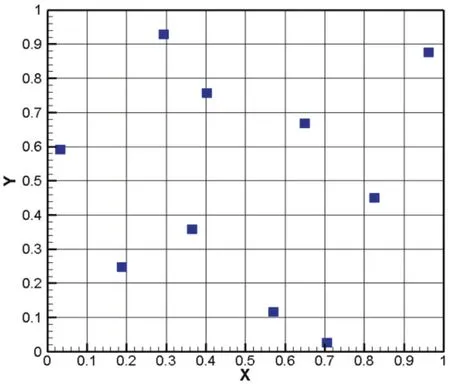
图3 二维采样分布

图4 三维采样分布

2.3 代理模型及精度验证

代理模型是指在不降低精度的情况下构造的计算量小、计算效率高但计算结果与高阶模型或试验结果相似的数学模型。本文使用Isight中的Kriging代理模型。Kriging模型是一种基于随机过程的估计方差最小的无偏估计模型，它通过相关函数作用，具有局部估计的特点。该方法最早由南非地质学者Danie Krige于1951年提出[9-10]，之前主要广泛用于地质界，用来确定矿产储量分布，目前已被广泛应用于各个领域，成为优化设计中比较有代表性的一种代理模型方法。

本文选取DOE结果中的10个点通过百分比平均相对误差来评价代理模型的精度，误差值小于0.1则视为合格。其误差分析结果见表1，如图5～图6所示。

表1 误差分析结果

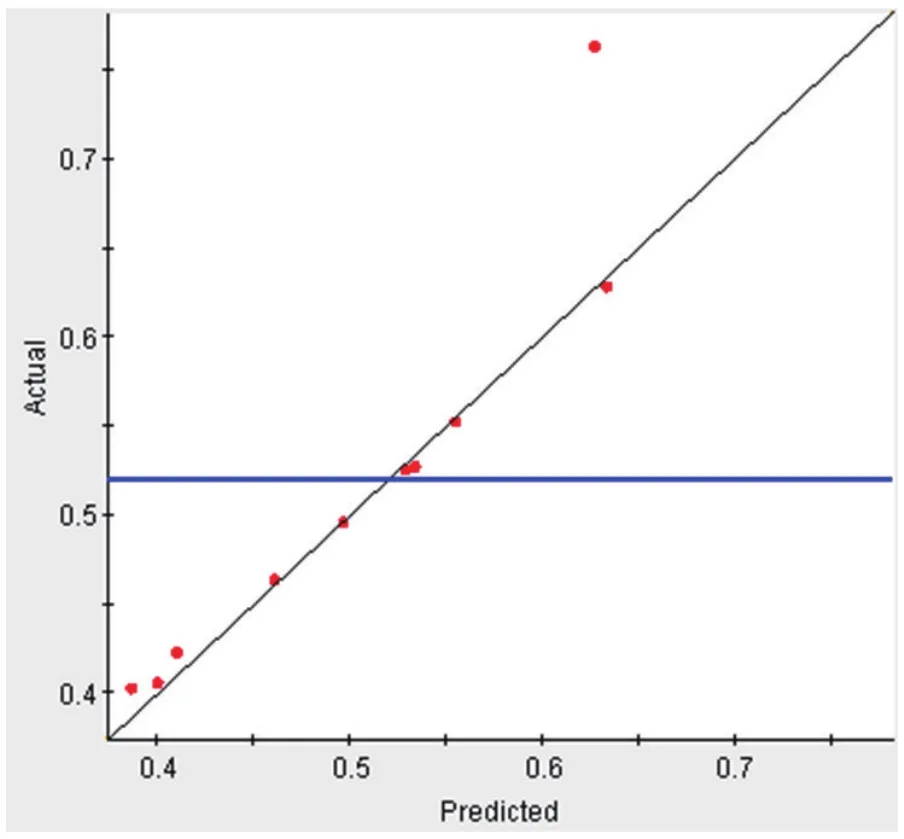
图5 轮芯应力误差分析

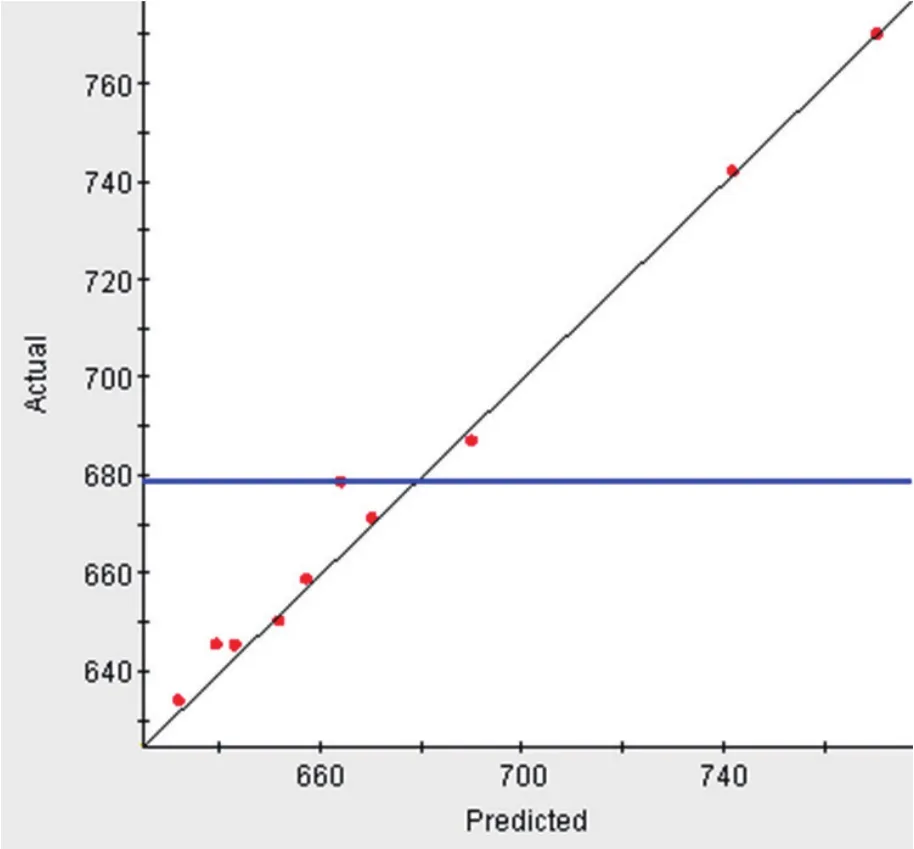
图6 总变形误差分析

2.4 优化算法

本次优化过程中共有10个设计变量，能够保证足够大的样本变化空间及良好的局部特性，并采用NSGA-Ⅱ（带精英策略的快速非支配排序遗传算法）多目标优化算法进行优化，种群大小设置为20，最大遗传代数设置为100代，交叉分布系数设置为10，变异分布系数设置为20。其中质量和应力为约束，总变形为优化目标。为进一步提高优化结果的精度，将求得的最优点进行结构强度计算，通过对比计算结果与预测结果，当计算结果与预测结果之前相差到某一设定值时，则认为该优化点为最优优化点；如果大于设定值，将该优化点继续添加到样本库中，然后重新建立新的Kriging代理模型，如此循环寻优，最终得到优化点。图7为寻优点结果对比图。

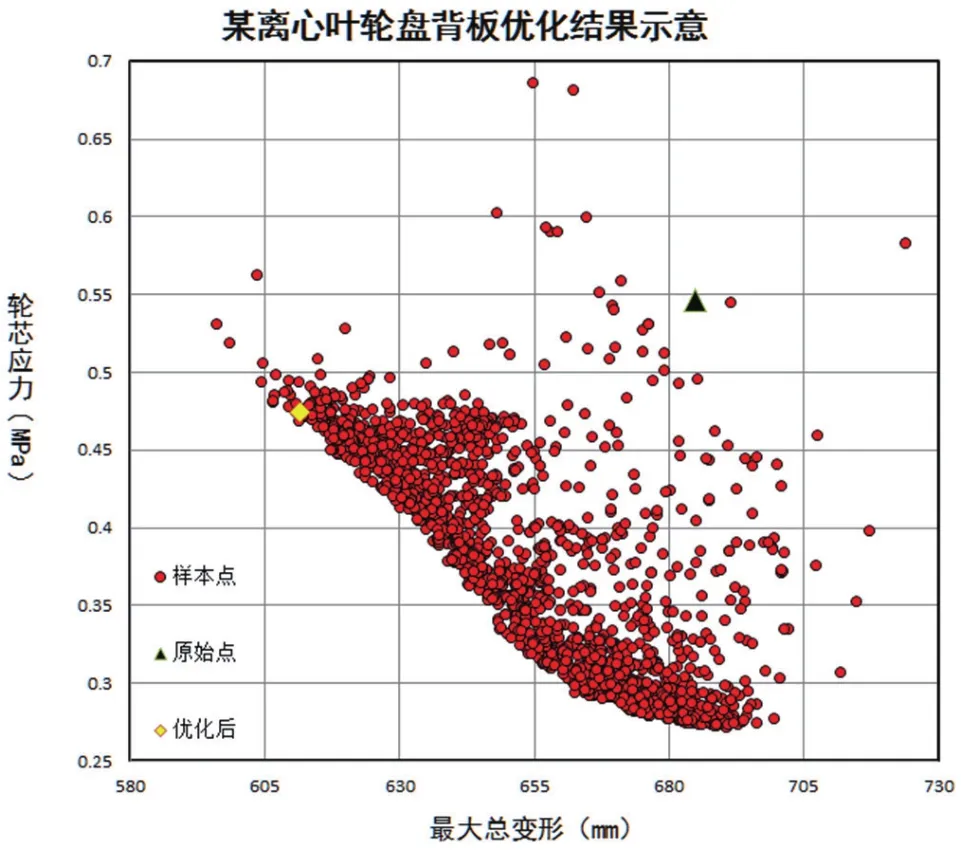
图7 优化结果对比散点图

2.5 优化结果与分析

图8～图10为优化前后方案、轮芯应力和最大总变形的对比，表2为优化前的原始点、通过NSGA-Ⅱ多目标优化算法推荐的优化后的点和优化后的实际计算点。通过对比可得，优化后的最大等效应力减小了6.3%，最大总变形减小了11.0%，质量没有增大。

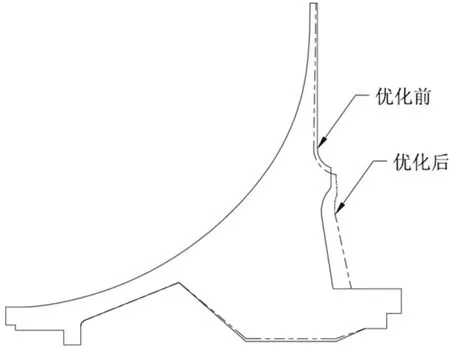
图8 优化前后方案对比

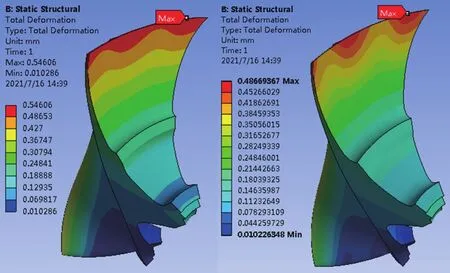
图9 优化前后轮芯应力

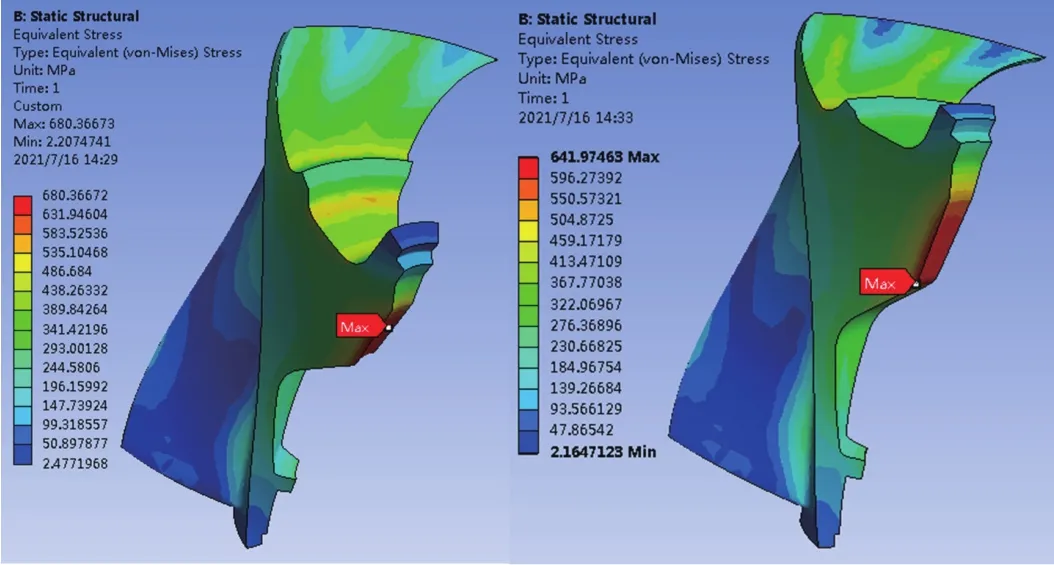
图10 优化前后最大总变形

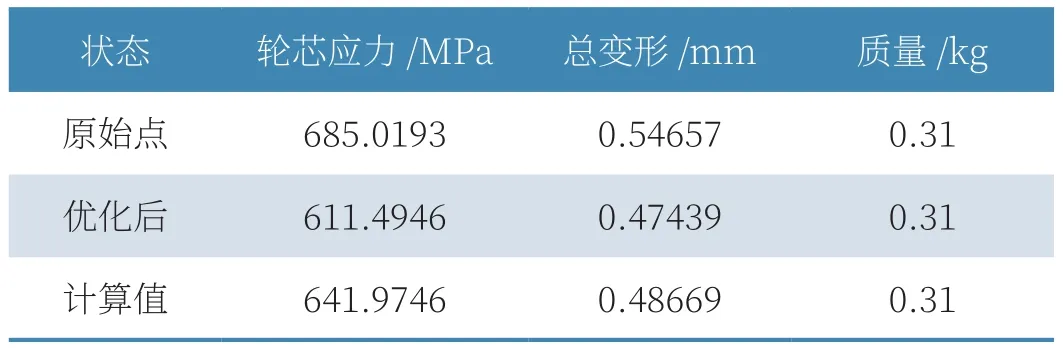
表2 优化前后的最大等效应力与最大总变形

3.结论

本文基于流固热耦合，采用实验设计方法结合遗传算法，以某离心叶轮背板为研究对象，对其结构进行优化，主要结论如下：

（1）优化后，在质量不变的情况下离心叶轮的最大等效应力减小了6.3%，最大总变形减小了11.0%，离心叶轮叶尖的区域变形量得到有效控制，有助于离心叶轮整体可靠性的提高。

（2）本文基于试验设计+Kriging代理模型+NSGA-Ⅱ的优化设计框架，极大提高了优化效率，可为离心叶轮的优化设计提供参考。