基于某叶型的任意中弧线叶型造型方法研究

刘才丽

（中国航发湖南动力机械研究所，中小型航空发动机叶轮机械湖南省重点实验室，湖南株洲 412002）

为适应发动机高推重比的发展目标，压气机的级压比和负荷不断提高，高负荷风扇是一个重要的发展方向。高负荷风扇压气机的主要特点之一就是叶型负荷大，包括进口马赫数高、叶型弯角大，常规叶型如双圆弧、多圆弧叶型已很难适应新的要求。

任意中弧线叶型是高负荷风扇压气机采用的造型方法之一，国内外开展了一系列的设计研究工作。Frost G R等人开发出了任意中弧线叶型叶片造型程序[1]，该方法建立在通流计算的基础上，根据流线曲率法气动设计计算得到的气流角，结合经验的攻角、落后角来确定叶型的中弧线。再将厚度分布叠加到中弧线上，得到叶型的坐标。北航的桂幸民老师[2]对Frost G R等人的方法进行了适当的改进，使其能同时适用于轴流、斜流和离心压气机叶片的设计。

已有的任意中弧线造型方法均是基于通流计算的结果，利用通流计算的结果得到中弧线的表达式，通流计算程序非常复杂。由于任意中弧线叶型造型方法的唯一特点体现在中弧线面的形成上，它的中弧线由多段多项式构成，因此作者考虑利用已有的性能较好的叶型，对其中弧线进行数学变换，得到类似此叶型的任意中弧线叶型的中弧线公式。此方法不再需要进行通流计算，因而造型方法相对简便。利用此方法可以进行已有叶型的改进设计研究。文中将以外文文献给出的某两级轴流风扇和某离心叶轮为例，进行任意中弧线叶型造型方法研究。

1.确定方法

1.1 设计思路

本文设计方法的总体思路是通过对已有某叶型的中弧线曲线进行数学变换，得到任意中弧线叶型中弧线的表达式；对原有的厚度曲线进行变换，得到任意中弧线叶型厚度分布表达式；再将厚度分布叠加到中弧线上，得到基元叶型的表达式。

对中弧线的变换主要是对中弧线直接求导，得到沿弦线各站位的几何构造角分布。将几何构造角代入到任意中弧线叶型中弧线表达式中，同时利用边界条件，求出表达式中的未知系数，得到中弧线表达式。

对厚度曲线的变换主要是通过分析厚度曲线，得到最大厚度点的X坐标以及最大厚度值。再利用前后缘的半径值，同时利用边界条件，最终求得任意中弧线叶型厚度分布的表达式。

在早期的叶型设计中，叶型头部几乎全部采用圆形头部的设计，经过长期的研究发现，椭圆形头部比圆形头部有更好的性能。因此，作者给出一种椭圆形头部设计方法，并将此方法加入到任意中弧线叶型设计方法中，使得此任意中弧线叶型设计方法拥有更好的性能。

1.2 确定方法

由确定方案的思路可知，任意中弧线叶型设计方法主要包括3部分，分别是中弧线、厚度分布以及椭圆形头部，下面将分别进行介绍。

1.2.1 中弧线

本文中所用的任意中弧线叶型采用多段四次多项式中弧线，四次多项式解析表达式如下：

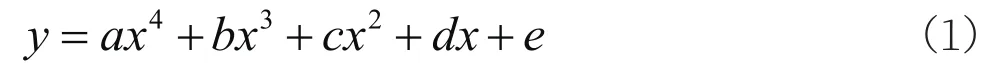
每一段的方程有5个未知系数，因此需要5个边界条件来确定这5个未知系数的值。首先，规定各中弧线段两端的二阶导数为零。

第一个中弧线段两端的边界条件如下：

第二个中弧线段两端的边界条件如下：

第三段，第四段……，都和第二段的边界条件一致。

由公式（2）和公式（3）可知，公式（2）是公式（3）的特例，区别在于：第一段中y1=0是一个给定的值，而后面各段中的y1是由前面一段四次多项式计算出来的值。

公式中的x1、x2由设计者确定，北航的桂幸民[2]认为，生成任意中弧线叶型的时候，叶片的前缘和后缘必须有一个计算站，除此之外，叶片排的内部应该再另外加上4个计算站，所以，一般应有6个计算站。这里，采用桂幸民的方法，中弧线由6个计算站组成，即将叶片的中弧线等分成5段。

同时，设计者需在每段的首尾处给定正切值tanβk1和tanβk2，各个β值由对原有叶型的中弧线求导得来。

由于公式（2）是公式（3）特例，因此，这里只需对公式（3）求解即可。将边界条件（3）带入到方程（1）中求解，求解的结果如下：

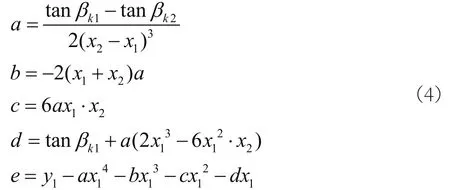
从第一段开始，当求出本段多项式的系数a，b，c，d，e后，将系数带回公式（1），求得本段末尾处的y值，并将这个值作为下一段的边界条件。

1.2.2 厚度分布

本文中所用的任意中弧线叶型厚度分布采用两段三次多项式样条函数。第一段样条函数用于定义前缘至最大厚度点，第二个样条函数用于定义最大厚度点至尾缘。在相交点，两方程的厚度、一阶导数和二阶导数值均相等。现在的压气机叶片一般都在高马赫数工况下工作，最大厚度点一般都在50%弦长以后，为防止前缘处的厚度分布发生负曲率，令前缘处二阶导数为零。前缘厚度等于前小圆半径，尾缘厚度等于尾缘半径。

两段三次多项式厚度分布曲线，每段需要4个边界条件来求解4个未知系数。每段给定的边界条件如下：

第一段：

第二段：

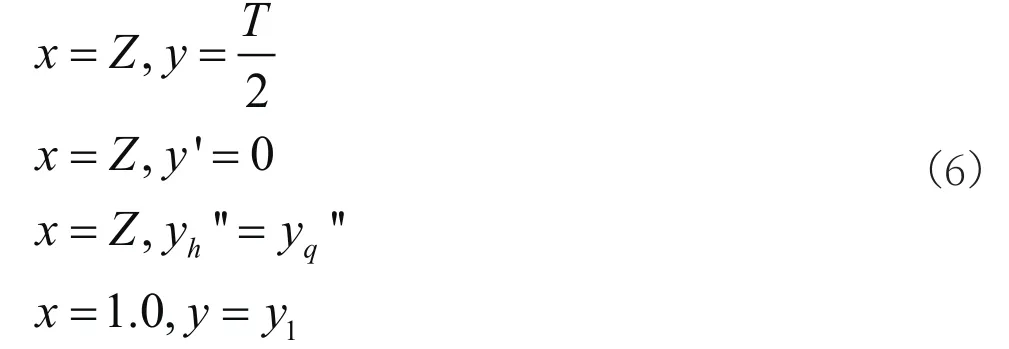
注意，这里y代表基元叶型的半厚度，T代表最大厚度，参数z代表最大厚度点在中弧线上的位置。

第一段厚度分布曲线，用简单的三次多项式来表示：

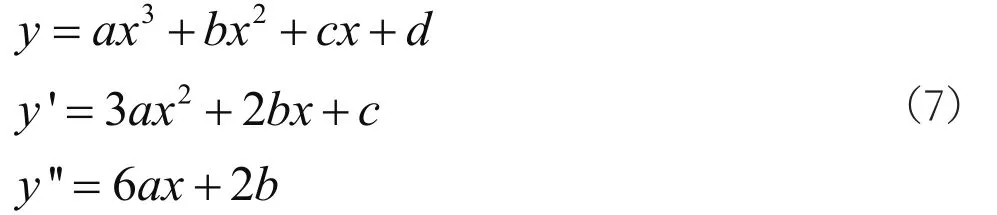
将边界条件公式（5）代入到方程（7），4个未知系数解出如下：

并且可以求得当x=Z时：

对第二段厚度分布曲线，用另一个三次多项式表示如下：

将边界条件公式（6）、（9）代入到方程（10），求得4个未知系数为：

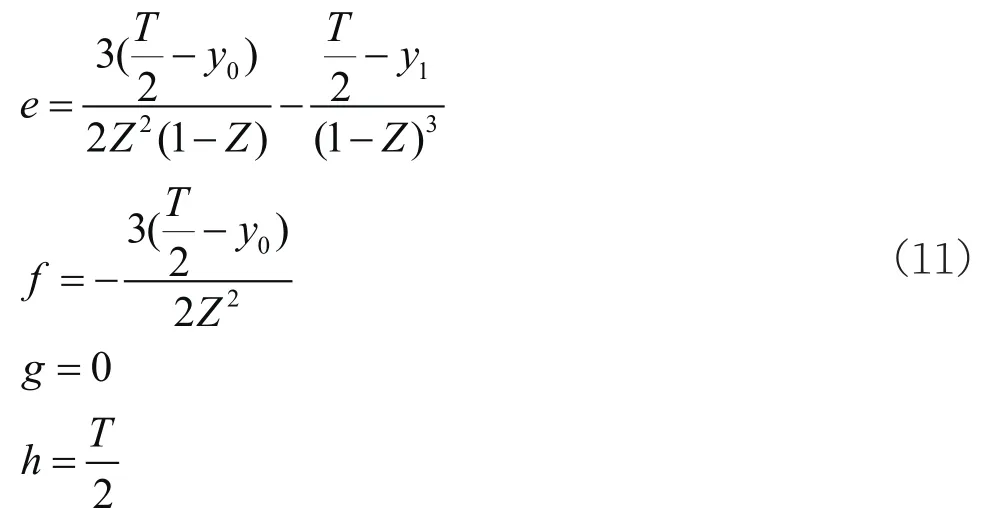
因为两段厚度分布曲线的方程均是三次多项式，所以，方程中有可能存在拐点。第一段厚度分布曲线，其中一个边界条件是令前缘处的二阶导数为零，所以，从前缘点到最大厚度点这一部分不存在拐点。对于第二段厚度分布曲线，存在一个最小值Z（最大厚度点位置），使得方程的拐点不出现在叶片表面上。给出Z最小为：

当前、后缘厚度相等时Zmin=0.5。随着后缘同前缘厚度比的增加，Zmin也逐渐加大。

1.2.3 椭圆头部

本文所用的任意中弧线叶型厚度分布采用椭圆形头部设计。

如图1所示，其中，O点是中弧线前缘点，直线F1F2是中弧线在前缘点的切线，线段de与直线F1F2垂直，将de方向作为椭圆的纵半轴，直线F1F2方向作为椭圆的长半轴。F1、F2是椭圆的两个焦点。O点的坐标是（x0，y0）；叶片长半轴、短半轴a/b=const.

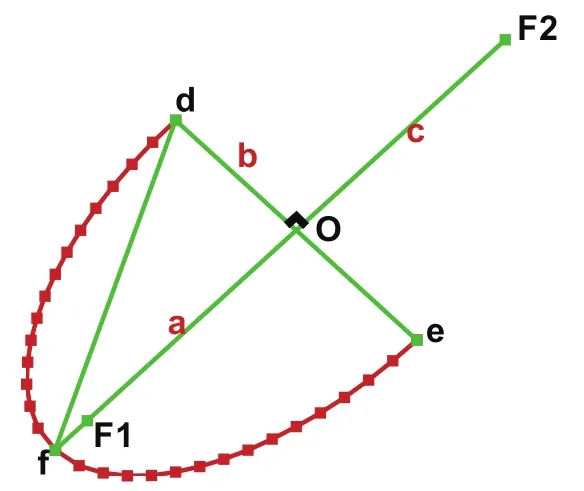
图1 椭圆形头部

直线F1F2与横坐标的夹角为α。那么：

F1、F2的坐标为：

位于椭圆上任意一点M（x，y），由椭圆的定义可知，M点距两个焦点的距离之和等于常数2a,所以有

约简之后则有：

对一个单独的变量x，这是一个一元二次方程mx2+nx+p=0，求解一元二次方程得到：

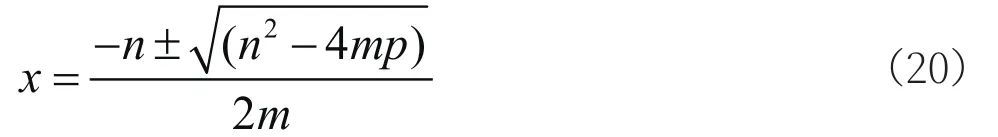
式（20）为最终求解得到的椭圆的表达式。

2.算例分析

利用以上介绍的任意中弧线叶型造型方法，对某两级轴流风扇和某离心叶轮进行造型分析。

2.1 两级轴流风扇

首先分析某两级轴流风扇，造型对象为国外发表的某两级风扇[3]。风扇的设计点流量为83.55kg/s，设计压比2.8，设计点绝热效率83.9%。风扇转子叶片和静子叶片均采用多圆弧叶型设计。

采用以上介绍的任意中弧线叶型造型方法，对此风扇再造型，最终得到的任意中弧线叶型再造型风扇如图2所示。

图2 任意中弧线叶型再造型风扇

用NUMECA软件对其进行数值模拟。数值计算结果如表1所示，将数值计算结果与原风扇性能进行对比，结果如下。

表1 原风扇和任意中弧线再造型风扇性能对比

从表1可看出，任意中弧线叶型再造型风扇相比原风扇效率和裕度均有提高。

2.2 离心叶轮

为验证此任意中弧线叶型造型方法同样适用于离心叶轮，现对NASA报告[4]上给出的某低速离心叶轮进行造型分析。

最终得到的任意中弧线叶型再造型离心叶轮如图3所示。

图3 任意中弧线叶型再造型离心叶轮

用NUMECA软件对其进行数值模拟。数值计算结果如表2所示，将数值计算结果与原始的离心叶轮性能进行对比，结果如下。

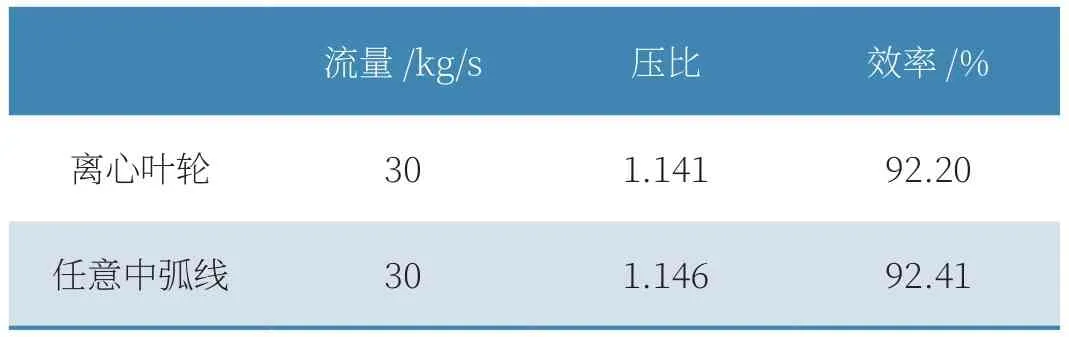
表2 离心叶轮和任意中弧线再造型叶轮性能对比

从表2可看出，任意中弧线叶型再造型离心叶轮相比原叶轮压比和效率均有提高。

3.结论

本文提到的任意中弧线叶型造型方法适用于已知叶型数据的情况，工程上可以用于已有叶型数据的改进设计研究。由文中可知，这种造型方法对于轴流和离心压气机均适用，再造型叶片性能相比原叶片性能均有提高。给出的任意中弧线叶型造型方法，为更好地研究任意中弧线叶型的性能提供基础。