孔隙塌缩对工业炸药爆轰的多重作用
李晓杰,王小红,王宇新,闫鸿浩
(1.大连理工大学运载工程与力学学部工程力学系,辽宁 大连 116024; 2.工业装备结构分析国家重点实验室,辽宁 大连 116024)
20世纪50年代中叶, 世界工业炸药进入了以廉价硝酸铵为主体的硝铵类炸药新时期。 随着工业炸药制造技术的高速发展,以及对爆轰机理认识的深入,猛炸药敏化剂已经逐步被取代。几乎所有工业炸药都是以各种形态的硝酸铵为氧化剂,油相为还原剂,辅助以表面活性剂、敏化剂的混合炸药[1-6],例如: 多孔粒状铵油炸药、粉状乳化硝铵炸药、膨化硝铵炸药、含水浆状炸药、水胶炸药、乳化炸药、重铵油炸药等。目前所使用的工业炸药的主要敏化手段均采用各种气泡、微孔隙,其敏化机理是基于气泡绝热压缩的“热点”机理[5-6]。人们对各种粉状、粒状硝酸铵的微观结构进行了深入的研究,阐述了硝铵炸药的自敏化机理[5,7-9]。对于各种含水炸药则采用各种化学型和物理型气泡作为主要敏化剂,如:在乳化炸药中采用亚硝酸钠、H发泡剂等化学发泡,或采用膨胀珍珠岩、空心玻璃微珠、空心树脂微球等物理敏化[5-6,10-12];浆状炸药[13-14]和水胶炸药[15-16]尽管使用硝酸甲胺、铝粉、硫等进行敏化,但也必须以化学或物理手段引入气泡,作为爆轰反应中心; 重铵油炸药是水胶炸药或乳化炸药与铵油炸药的掺合物[5-6],气泡依旧对爆轰反应起着重要作用。随着研究的深入,人们对炸药内部的微观结构与宏观性能之间的关系也进行了大量研究,提出了孔隙(气泡)均匀性影响热点形成时间的均一性[17],以及孔隙形态分布影响炸药敏感度等问题[18]。另外,随着人们对炸药压力减敏的研究,静压力和动压力压缩孔隙使其体积减小,也被认为是压力减敏主要原因[19],静压下的爆速测试也显示了与炸药密度增高一致的“压死”现象[20-22]。与此同时,由于军工对高能炸药安全性的要求更高,以及对起爆机理深入研究,人们对冲击波作用下微孔隙“热点”问题进行了大量的研究[23-25],包括使用大型离散元或无网格法等流体动力学计算程序对“热点”的形成与发展进行模拟[26-30], 甚至进行了模拟实验[30]。大量研究结果都体现了孔隙的非对称塌缩,使人们认识到孔隙对炸药的点火作用不仅只是依靠气体压缩高温,还有孔隙闭合产生的射流,以及由射流冲击引起的高压与剪切高温。这极大地丰富了人们对“热点”机制的认识,但对于孔隙塌缩的研究仍限于炸药“点火”,尚缺乏对后续爆轰过程的研究。
从工业炸药的爆轰过程来看,是典型的非理想爆轰。对于非理想爆轰,人们已经认识到是由于爆轰反应能量无法全部供给爆轰波而引起的[31-32]。加之近期对含铝炸药的深入研究,人们对铝粉之类的“后燃反应”(或称“二次反应”)理解更加深刻[33-37]。将含铝炸药的非理想爆轰反应能量释放分成“快过程”和“慢过程”, 爆轰CJ面前方的“快过程”反应能量供给爆轰波并维持其传播,CJ面后方的慢反应过程只能引起爆轰产物膨胀,对爆轰波强度没有贡献。针对这一问题,人们建立了JWL-Miller等爆轰产物状态方程对“后燃反应”加以描述[38-39]。
事实上,很早人们就提出了爆轰中有湍流存在[40-41],但仅限于对现象观测研究。加之,通常对炸药爆轰反应区的观测手段都是基于测量化学反应的,只能测得化学反应区厚度δc[42],所以一直认为爆轰波的传播只与化学反应相关,并未有深入考虑湍流释能及其作用的问题,甚至认为湍流对爆轰的贡献可以忽略。
本文通过对爆轰反应中孔隙的压溃过程进行研究,提出了工业炸药中孔隙压溃不仅产生“热点”点火因素,孔隙闭合所产生的旋涡运动还具有强烈的搅拌混合作用,可促进爆轰的化学反应;而在CJ面之后残存的涡动能与压力波动,又会起类似“慢反应” 的作用,对爆轰反应能量产生耗散。在此基础上,提出了由化学反应区与湍流热耗散区共同构成支持炸药爆轰波的“释能区”设想,通过理论推导与分析,对工业炸药的极限直径、临界直径、最佳装药密度、高密度“压死”、炸药能量利用率、乳化炸药敏化孔隙直径等问题之间建立了内在联系。
1 工业炸药非理想爆轰现象与问题
1)爆轰的极限直径大。早期研究认为,多孔粒状铵油的极限直径甚至能达到9 m以上[43]。在杜邦公司编制的手册中[44],多孔粒状铵油在直径356 mm炮孔中的爆速不到4.75 km/s,远小于5.4~5.5 km/s的理论值。随着国内工业炸药研究进展,对二级岩石炸药的爆速要求达到3.2 km/s以上,一级的达到4.5 km/s以上[45],实际粉状(粒状)铵油炸药在炮孔中的爆速可达4.0~4.7 km/s,乳化炸药和重铵油炸药在储存初期的爆速均达4.0~6.0 km/s,这说明不同品种的工业炸药能量利用率有差别,但均未达到理想爆轰状态。
2)爆轰的临界直径大。这与极限直径大是一致的,即使是优质的工业炸药,临界直径通常也在10~30 mm[46-47]左右,有的多孔粒状铵油炸药临界直径甚至达到40~50 mm[43]。
3)存在高密度“压死”问题。工业装药存在最佳装药密度,超过该密度后爆速会随着密度增加而急剧下降,直至失去雷管感度,即所谓的“压死”。粉状或粒状铵油炸药装药密度增加到1.2~1.3 g/cm3时, 炸药爆轰就会出现“压死”现象[43,48],而该装密度仅是硝酸铵晶体密度(1.72 g/cm3)的70%~76%。研究表明[49],根据敏化方式的不同, 乳化炸药的最佳密度在1.07~1.15 g/cm3之间,超出1.15~1.24 g/cm3则失去雷管感度,该密度约为乳化炸药基质密度1.426 g/cm3的80%~87%。如空心玻璃微珠敏化乳化炸药[50]密度1.19 g/cm3时能量输出最大,密度至1.21 g/cm3以上时水中冲击波能量急剧下降,失去雷管感度显现出爆燃性质;另外,无论是静压或动压作用下,乳化炸药都存在减敏问题[19-20,51]。
4)爆轰与孔隙尺度相关。炸药爆轰性能与硝酸盐和油相的预混合程度有关是毋庸置疑的,也与炸药的孔隙尺度和数量相关。粉状炸药的爆轰与粒度密切相关,多孔粒状铵油炸药与膨化硝铵炸药、粉状乳化炸药相比,无论在感度、爆速、猛度上都有很大区别。甚至单质炸药,粒度也影响其爆轰性能,作者曾做过粉状与鳞片状TNT的爆速对比试验,在66 mm塑料管中测得粉状TNT的爆速为4.0 km/s(密度0.77 g/cm3),而鳞片状TNT只有2.9 km/s(密度0.89 g/cm3)。发射药研究表明[52],粒度越小爆速越高。乳化炸药的研究也表明[49,53],采用粒径33~566 μm的空心玻璃微珠敏化时,其极限直径和各种感度均随微珠粒径增大而增大;在炸药密度为1.10 g/cm3、空心玻璃微珠粒径为125 μm时释放热量最高。
5)爆轰能量利用率低。这点与实际工业炸药没有达到极限直径有关。根据CJ理论,可以推导出爆速D与爆热Q关系如下
D=[2(γ2-1)Q]1/2
(1)
式中:γ为多方指数,实际上代表了爆轰波后体积的压缩比。对于高能炸药γ在3左右,对于工业炸药γ在2.0~3.0之间。
式(1)是人们非常熟悉的公式,之所以在实践中并不使用,这是因为人们发现爆轰有很大的能量损失,公式只能计算理想爆轰速度;对于非理想爆轰而言,计算误差太大。为此,本文设想用实验爆速Ds反向计算爆热,将计算的爆热看成是供给爆轰波的实际爆热Qs,然后再与理论爆热值Q进行比较,从而估算出能量利用率ζ,可得到计算公式如下
(2)
由于实践证明,高压高速时的γ要大于低压低速的γs,故而爆轰波的能量利用率ζ不会大于(Ds/D)2。以铵油炸药为例,理论爆速D约为5.4 km/s,常用炸药爆速为3.2 km/s,按式(2)计算出的爆轰波的能量利用率ζ只有35.1%;即使在炮孔中爆速达到4.7 km/s,计算出的ζ仍只有75.8%,由此可见工业炸药爆轰的能量利用率之低。
从上述对工业炸药的非理想爆轰情况的总结来看,单纯认为炸药中孔隙只起“热点”作用就有所偏颇了。首先是,如果认为炸药中的孔隙仅是起爆的“热点”,只是化学反应中心,那么只要炸药中热点数目足够多就可以正常激发炸药爆轰。这可以解释在一定的粒度范围内为什么炸药粒度越小爆轰速度越高;也可以解释为什么乳化炸药中敏化气泡有最优尺寸。但“只要炸药中热点数目足够多就可以正常激发炸药爆轰”的观点,却不能推衍出炸药爆轰性能与密度相关的事实;更不能解释工业炸药中存在的最佳密度和爆轰“压死”问题。由最佳密度和爆轰“压死”现象显然可见,在工业炸药爆轰中孔隙压溃必然不只是起单一的“热点”作用;还一定存在着孔隙非对称压溃形成的“搅拌混合”,促进爆轰反应的化学物质传输(传质),加快燃烧反应的作用。可是既然有了化学反应起因的“热点”,也有了促进化学反应的“搅拌混合”,可为什么爆轰波能量利用率只有35.1%~75.8%?大量的爆轰能量损失的原因又是为什么?这个问题显然需要细致研究爆轰波中能量的输运过程才能得到解答。
2 炸药中孔隙的高速塌缩
如前所述,要研究爆轰反应区中的能量输运过程,就必须研究孔隙塌缩在爆轰反应中的行为。在一维炸药爆轰理论中,最常用的是CJ条件和ZND模型。CJ条件指出为了维持爆轰波稳定传播,爆轰波后应该是超声速区,这样紧邻爆轰波面后方的就是声速面,也就是CJ面。Zeldovich(Зельдович), Von Neumann和Doering[54]将CJ模型加以发展,考虑有限反应速率,得到了含有爆轰反应区的ZND模型(见图1)。如图1a所示,图中以稳定速度D向左方未反应的炸药中传播一道前驱冲击波;前驱波后炸药开始逐渐反应,即为爆轰反应区;反应区之后连接着CJ面,CJ面的传播速度同样是D,以保证反应区宽度稳定不变;前驱波、反应区和CJ面构成整个爆轰波。将坐标系设定为随爆轰波D一起运动,可得到如图1b的定常流动模式,即前驱冲击波和CJ面都驻定不动,未反应炸药以D流入爆轰波区域,以D-ucj流出CJ面。为保证CJ面不受其后方流动的扰动而保持稳定,CJ面应是超声速的,至少为声速面,即得到熟知的CJ条件:
acj=D-ucj
(3)
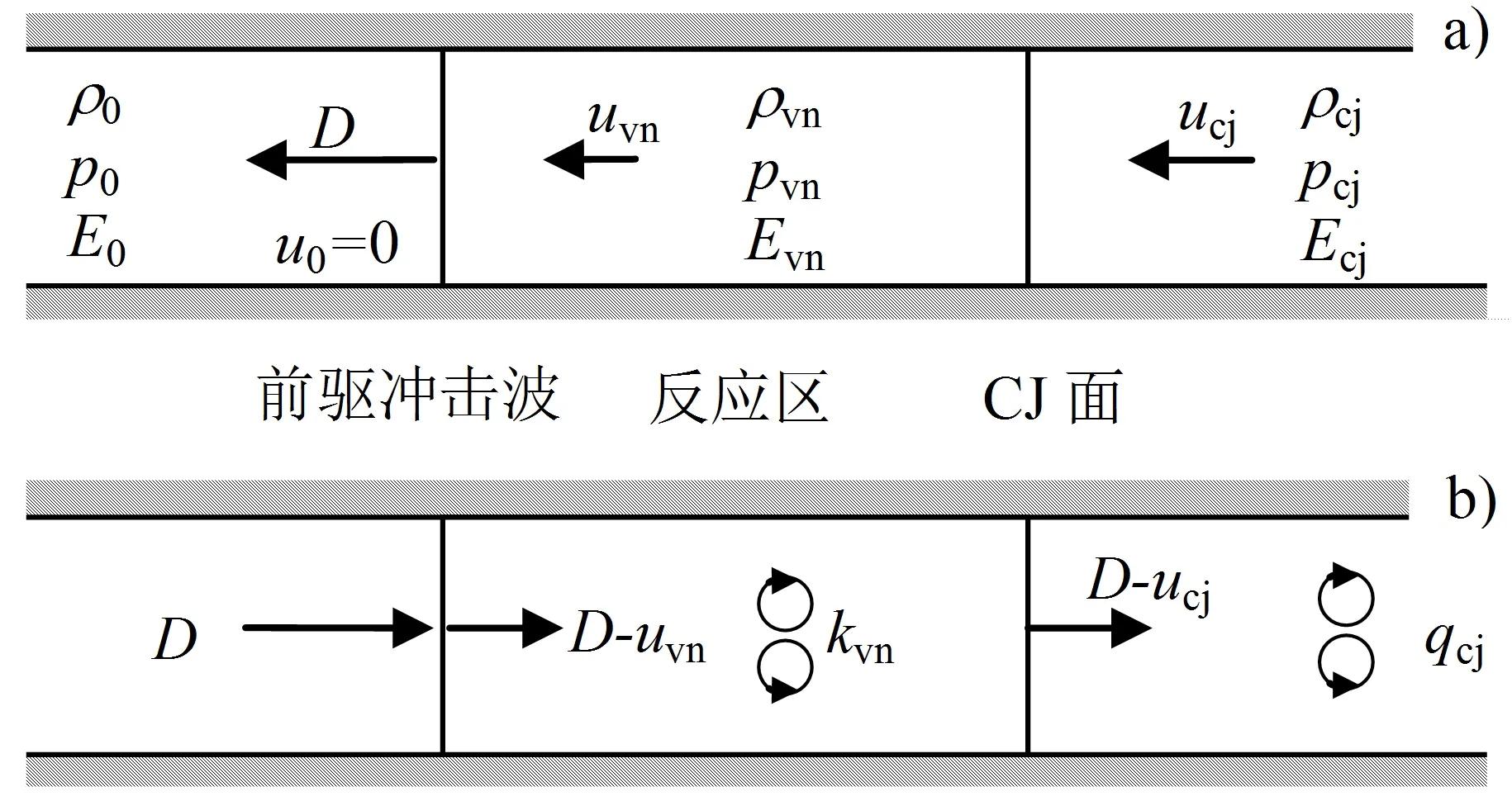
图1 ZND爆轰模型Fig.1 ZND detonation model
炸药爆轰的压力波形如图2所示。压力波形的前方即是前驱冲击波,显示出在未反应炸药中传播的又高又陡的Von Neumann峰。Von Neumann峰后炸药迅速反应,压力陡然下降至平缓坡段。压力曲线发生突然转折的点,即是CJ点。Von Neumann峰和CJ点之间即是反应区厚度δ,对于高能炸药约为0.1~2.0 mm,工业炸药在1~10 mm量级[42]。

图2 爆轰压力波形Fig.2 Detonation pressure waveform
显然,当未反应炸药中存在孔隙时,前驱冲击波会将孔隙高速压溃,在孔隙周边产生局部的能量沉积,因此,人们对孔隙压溃的“热点”点火效应进行了大量的研究[23-30]。实际上未考虑炸药反应时的孔隙压溃过程,与一般多孔材料在冲击波下的行为无异。大量多孔材料冲击的细观力学研究表明,材料孔隙度越大,冲击波作用下能量沉积越多,其能量的沉积是微射流、微冲击、微摩擦、微孔隙塌缩作用的结果[55-58]。
光滑粒子动力学方法计算的颗粒碰撞情况如图3所示,冲击波仅以200 m/s质点冲击速度由上向下挤压铜颗粒,在a、b两种类型的孔隙中都有微射流产生,并冲击其相对应的颗粒表面[56]。可见高速冲击在粉末中引起的孔隙塌缩会产生微射流、微冲击、微摩擦,以及到最终压合时的极微小孔隙的对称闭合,在产生射流和射流冲击之处必然会产生“热点”。实际上,这些微运动不仅产生了高速的能量沉积,还产生了物质输送与传递的作用;而传统的气体绝热压缩“热点”的模型,仅仅是多孔材料中能量沉积机制之一。微射流、微冲击、微摩擦都代表着孔隙中强烈的剪切与碰撞,都会发生热量沉积,不仅形成新的“热点”点火机制,而且还会发生强烈的湍流传质,对“热点”附近的炸药燃烧与燃烧扩散起积极的混合助燃作用。通俗地说,孔隙塌缩起到了“热点”点火和“搅拌”促进燃烧的双重作用,使炸药在“热点”附近“边搅拌边燃烧”,加快了爆轰反应速度。

图3 粉末颗粒间高速碰撞的数值模拟结果Fig.3 Numerical results of high speed impact between powder particles
对于乳化炸药敏化气泡的高速冲击问题,人们也已经进行了大量的研究[25-30],认识到与粉末相类似的非对称运动现象。文献[59-60]发现了冲击后气泡的细化破碎,文献[30]观测和计算了气泡非对称塌缩,文献[26-29]对气泡塌缩采用多种计算方法进行了模拟计算。但是限于对炸药“热点”作用的研究,均没有探讨气泡塌缩后的运动状态。为此,本文采用无网格物质点法(MPM)对气泡塌缩过程进行计算,计算结果如图4和图5所示。中心部位为半径r=0.5 mm的球形空气泡,周围为以滑移刚壁围绕的直径2 mm水柱,并用红色标识球孔内壁的水层,以方便观察研究其流动。考虑到水和气泡的可压缩性,令水与气泡以恒速u撞向底部刚壁,撞击速度分别为800 m/s和2 000 m/s。以800 m/s速度撞击的物质质点运动如图4所示,以2 000 m/s撞击的压力云图如图5所示。

图5 气泡冲击溃灭的压力云图(2 000 m/s)Fig.5 Pressure nephograms of bubble shock collapse(2 000 m/s)
由质点运动图4可见,撞击后气泡即开始发生非对称溃灭,气泡底部液体开始形成向上射流,与向下运动的气泡顶部液体发生撞击,理论上撞击速度可达2u,与实际观测结果相吻合,0.62 μm时气泡上下即将开始碰撞。当下方射流与气泡顶碰撞后,会形成向两侧翻转的“蘑菇云”状涡环,涡环包裹气体不断旋转并向上运动。涡环的旋转使气泡破碎并与液体混合,这会对炸药燃烧反应起到混合促进作用。再者,应该注意的是涡环会处于较长时间的旋转运动;可以想见,根据涡量守恒定律,在不考虑流体黏性与可压缩性的情况下,即使发生化学反应,涡环也会一直旋转不停,所携带的能量也不会耗散。由图5的压力云图可见,气泡的冲击压溃会伴生着来回传播的压力波。显然,如果没有黏性耗散,压力波携带的能量也不会减少。涡旋和压力波所携带的这种紊乱的机械能量显然不能对外作功,需要转化为热能,依靠加热爆轰气体提高内能才能对外作功。这就带来了一个问题,即是涡旋和压力波所携带的紊乱机械能究竟有多少?这些紊乱的能量是否会在CJ面之前完全提供给爆轰波?这就涉及到孔隙塌缩的第三个作用——“湍流能量耗散” (turbulent dissipation)向热能的转化。
3 孔隙塌缩对炸药爆轰性能的影响
为了探究旋涡和压力波动所携带的能量,就必须从爆轰模型上研究炸药整体孔隙压溃的总能量。如图1中带爆轰反应区的ZND模型所示,如果考虑在前驱冲击波后携带了涡动和波动的湍流能量kvn,通过CJ面后的能量损失为qcj,其余参数如图1所示,ρ、p、u、E、H分别代表密度、压力、质点速度、单位质量比内能、单位质量比热焓。参照图1b中的定常流动坐标系,并注意到湍流对压力、速度、密度量的平均贡献为0,按质量(流量)守恒、冲量定理和伯努利形式的能量守恒方程,可得下式

(4)
CJ面上的冲击波关系式如下:
(5)
由式(5)结合CJ条件式(3)即构成含湍流的爆轰波方程,在引入CJ面对湍流能量kcj与爆轰产物状态方程后,即可求解爆轰波。式(5)与常规的爆轰波方程形式上区别很小,仅是在维持爆轰波的能量项上扣除了能量损失qcj。所以只要以(Q-qcj)替代常规爆轰波方程中爆热Q,现有的爆轰波公式就都可以正常使用。这也从另一方面说明了以式(2)估算爆轰波能量利用率ζ的合理性。但以式(2)估算多孔粒状铵油爆轰波能量利用率ζ只有35.1%~75.8%,能量损失qcj/Q竟然高达64.9%~24.2%。要进一步探究爆轰能量利用率高低的原因,可由炸药的孔隙压溃过程加以研究。
多孔与密实炸药的未反应Hugoniot关系曲线如图6所示,图中虚线S为密实炸药,实线为多孔炸药,两条斜直线分别为多孔与密实炸药的Rayleigh线。比容V=1/ρ,δV为未反应多孔炸药与密实炸药在冲击压力pvn下的比容差,是两者压缩后的内能差造成的热膨胀结果[61]。设密实炸药的冲击Hugoniot能量方程如下
考虑到其初始比内能与多孔炸药的相同。将上式与式(4)的能量方程相减,并注意δV=Vvn-Vs=1/ρvn-1/ρs,可得
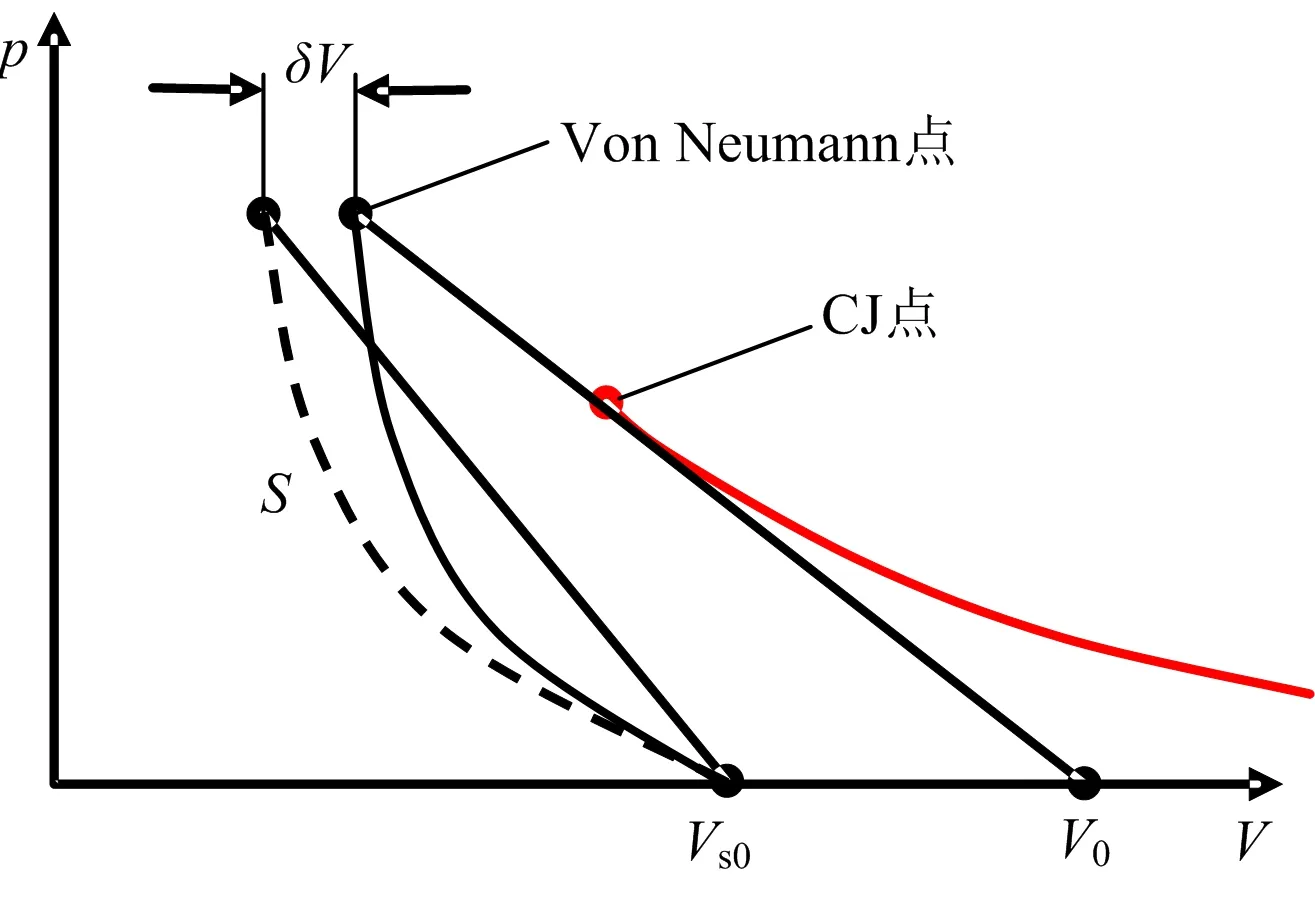
图6 多孔与密实炸药的Hugoniot关系Fig.6 Hugoniot relationship of porous and dense explosive

kvn=(pvn+p0)(1/ρs0-1/ρ0)/2
(6)
式(6)实际上是Von Neumann点的最大湍流能量。另外,如图6所示,Von Neumann点和CJ点在一条Rayleigh线上,即保证前驱波与CJ面的波速都为D是保持爆轰波稳定的必要条件。由式(4)和式(5)的质量守恒与动量守恒关系(未使用能量关系),并设ρcj=ρ0(γ+1)/γ,以γ代表爆轰波CJ面上的压缩率,可得
(7)
在δV=0时,如果已知未反应密实炸药的冲击Hugoniot关系,并确定爆轰波CJ面的γ值,即可求得爆轰波Von Neumann点和CJ点关系。使用文献[62]的乳化炸药基质的冲击试验点进行数据拟合,获得Hugoniot曲线:
(8)
将式(8)与式(7)结合,可以求出各种Von Neumann点状态所对应的爆速D(即Rayleigh线),进而可以求出不同γ值对应的CJ点,如图7所示。以式(6)和式(2)计算出Von Neumann点和CJ点的湍流能量与爆热Q的比率,如图8所示。计算中取炸药密度为1.10 g/cm3, 乳化基质密度为1.40 g/cm3,Q取3.0 MJ/kg3。
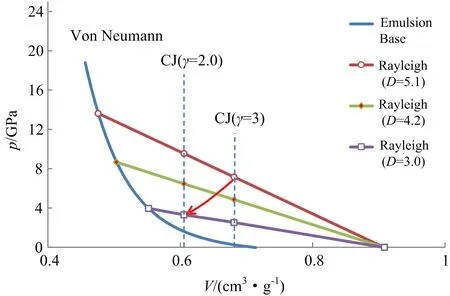
图7 乳化炸药的ZND爆轰关系Fig.7 ZND detonation relationship of emulsion explosive

图8 乳化炸药爆轰的能量分布Fig.8 Detonation energy distribution of emulsion explosive
如图7中箭头所指,当爆速减低使CJ点下移时,爆压下降使γ减小,爆轰对气体产物的压缩率反而是增加的。这就使CJ点与Von Neumann点的压力差变小,也是低速爆轰时很难测得乳化炸药Von Neumann点的原因[63]。由图8可见,CJ面上的能量损失qcj随爆速提高而下降;由于爆速高时γ值增大,所以实际的qcj曲线应如图中虚线所示。在达到理想爆速时,爆热全部提供给爆轰波,CJ面湍流能量qcj=0。图8显示Von Neumann点的湍流能量kvn随爆速提高而增加,说明湍流搅拌混合的能量增加,利于化学反应充分进行。在低爆速端湍流能量kvn很低,显示搅拌作用降低,燃烧不充分,致使CJ面上化学反应未能充分完成,qcj比例很高。在高爆速端,湍流能量kvn高于qcj,说明该段由于强烈的孔隙压溃涡流搅拌作用使燃烧反应很充分,CJ面的能量损失qcj应是湍流能量kvn尚未耗散为热能的残留部分。
如前所述,涡旋和压力波所携带的这种紊乱机械量kvn不能供给爆轰波,反而需要转化为热能,依靠提高爆轰气体的热内能供给爆轰波。这与通常的湍流问题研究是相反的,在一般湍流问题中湍流能转化为热量是能量损失,被称为“耗散”。而爆轰中恰恰需要加快湍流能量kvn向热能的“耗散”,使kvn通过热能供给爆轰波,所以在爆轰波中kvn向热的耗散是对爆轰过程有利的。而ZND爆轰模型中的“反应区(Reaction Zone)”则应是化学反应与湍流耗散热释能的共同作用结果,故应称为爆轰“释能区(Energy Release Zone)”则更为准确。
为了研究kvn的耗散过程,需要建立简单的旋涡和压力波的粘性耗散模型。由于爆轰“反应区”非常薄,只有1~10 mm,加之冲击波产生的是完整的涡环,且只向前方单向运动,不容易碰撞破碎。因此,不考虑旋涡向小尺度旋涡的能量传递,即假设旋涡不发生破碎。由于旋涡不破碎,压力波的频率特征也就不发生变化。当旋涡不变时,由前面的研究可见,涡环运动的特征长度即是气泡半径r,其特征速度为u,由此可见涡环的应变率与u/r成正比。考虑压力波的来回波动,压力波波长的特征长度也应是气泡半径r,波动频率显然也正比于r/D。而剪切运动应变率和波动的频率在黏性流体中都代表了耗散特征量,可得到黏性应力为
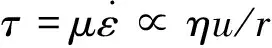
单位质量粘性功耗为
上式中的u2项正比于旋涡或振动能量k,并进一步注意到u2∝k=knv-q,设比例常数为A,并代入上式,可得
dq=Aμ(kvn-q)ρ-1r-2dt
将上式经移项积分求解,并注意到q的初始值为0,可得
ln(1-q/kvn)=-Aμρ-1r-2t
由于波后流速为D-uvn,则有耗散区厚度δd=(D-uvn)t,将之连同式(4)的质量守恒式一起代入上式,可得
当用一种已知参数的炸药(下标0)作为参考时,可以得到如下关系
(9)
上式很难具体求解,但仍然可以分析炸药孔隙尺度影响问题。假设某种炸药的参数完全已知,另一种炸药除孔隙尺度r外都与其相同,要达到同样的能量耗散比率,可得
δd/δd0=(r/r0)2
(10)
可见耗散区厚度δd按孔隙尺度r平方率增长。如果r0=0.05 mm,r=0.25 mm,孔隙尺度增加5倍,则耗散区厚度增加25倍。如果耗散区厚度δd与炸药极限直径成正比,假设孔隙半径r0=0.05 mm的炸药极限直径为15 mm,则孔隙半径r0=0.25 mm的炸药极限直径就为375 mm。低于该直径使用时,即便化学反应已经完全结束,但由于湍流能量尚未全部转化为热能,无法供给爆轰波,因此只能以“慢反应”形式在爆轰产物膨胀区释放。由此可见,炸药孔隙对爆轰的影响不仅仅是炸药“热点”数目的问题,孔隙尺度和密度同样非常重要。
另外,还应注意的是尽管式(10)显示孔隙尺度越小越好,但并没有考虑炸药各相的均匀程度。当考虑各相粒度时,就可得到孔隙尺度不能过小的结论了。乳化炸药基质的显微结构如图9所示,炸药的剂粒径集中分布在0.5~10 μm之间[6,12,22,64],中粒径为5~6 μm。可见,孔隙尺寸需要与炸药粒径相匹配,直径小于1 μm的孔隙对氧化剂和油相的混合作用较小,0.1 μm以下的孔隙基本上只能作用在氧化剂或油相的单相中,混合作用和热点作用都非常小。综合考虑热点、混合和旋涡耗散作用,乳化炸药敏化孔隙直径应与粒径相同或高一个数量级,过大的孔径湍流损失较大,所以在5~100 μm为最佳, 这与文献[22,50]等的试验结果一致。

图9 乳化炸药基质的扫描电镜照片Fig.9 SEM of an emulsion explosive matrix
4 装药密度对炸药爆轰性能的影响
除孔隙尺度外,影响爆轰性能的因素还有炸药的孔隙度,即装药密度。按照上节的计算方法,由0.9 g/cm3至1.40 g/cm3改变乳化炸药的密度计算出Von Neumann点的湍流能量kvn如图10所示。由图10可见,随着装药密度的增加,湍流能量kvn下降;当密度增加至无孔隙的基质密度时,kvn降为0。实际上,在研究装药密度对爆轰性能的影响时,已经发现不同直径的炸药其最佳密度和临界直径是不同的。
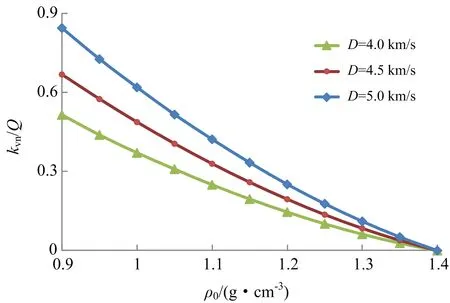
图10 湍流能量kvn与装药密度关系Fig.10 Turbulent energy kvnvs. charged density
乳化炸药装药密度对爆轰速度的影响曲线如图11所示[63,65],由图可见,对于一定直径的装药而言,随着密度的增加,首先出现最佳装药密度,其爆速最高,代表着爆轰能量利用率最高; 最佳装药密度之后,随着密度的增加爆速下降,下降速率很快,直至熄爆。熄爆对应的密度被称为该装药直径的“临界密度”,反过来说,这个装药直径也是该装药密度下的临界直径。另外,如图11中实线箭头及虚线箭头所示,“最佳密度”和“临界密度”都随装药直径的增大而增加,这表明,炸药极限直径必然随着装药密度的提高而变大。注意到炸药极限直径与释能区厚度成正比,极限直径变大也就意味着炸药爆轰释能区厚度随密度增加而变大了。爆轰释能区厚度随密度提高而增加,显然与湍流混合能量降低有关(见图12),搅拌混合效应的降低使化学反应也变缓,直到装药密度达到基质密度,孔隙搅拌混合作用彻底失去,炸药爆轰进入另外的点火机制。
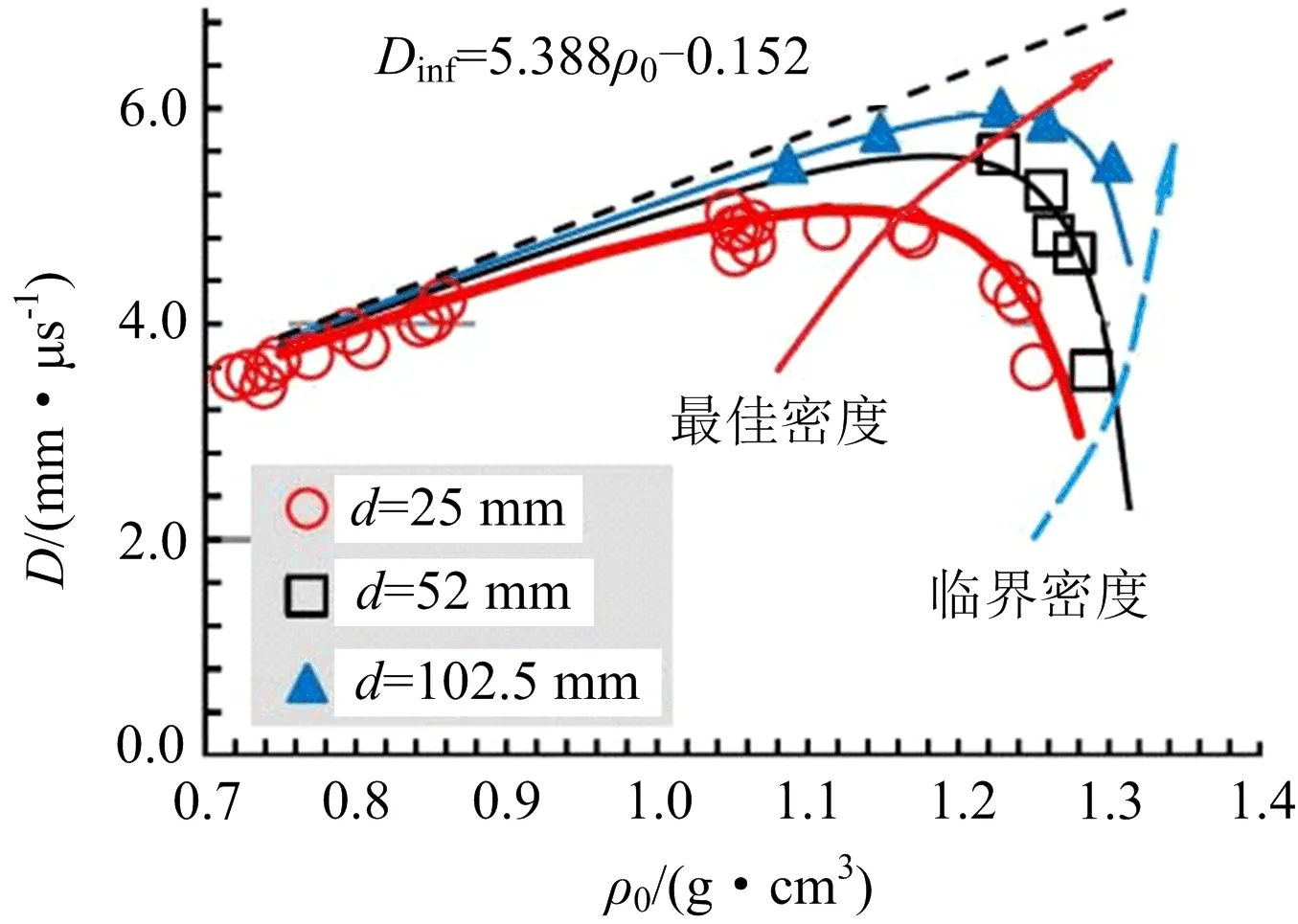
图11 乳化炸药爆速与装药密度关系Fig.11 Detonation velocity vs. charged density of emulsion explosive

图12 各种能量释放区厚度与装药密度关系Fig.12 Various energy-releasing thicknesses vs.charged density
由此可见,炸药释能过程是化学反应与湍流耗散竞争的结果,各种能量释放区厚度构成如图12的关系。装药密度ρ0较低时kvn值较大,搅拌混合促进燃烧作用强,化学反应快,但湍流耗散较慢;所以化学释能区δc小而湍流释能区δd较大。高装药密度端kvn较小,搅拌混合促进燃烧作用弱,化学反应变慢,但湍流耗散变快;所以化学释能区厚度超过湍流释能区厚度。因此,要使所有能量都提供给爆轰波,释能区厚度δ就必然取化学和湍流释能区的最大值,综合结果如图12中的实线所示,该实线显示释能区存在一个最小厚度。如果炸药直径固定,该最小厚度对应的装药密度就是能量利用率最高的,即最佳装药密度。对各种能量释放区厚度与装药密度关系的分析,还可以获得一个新结论,即工业炸药的高密度“压死”并不是其特有的现象。因为,炸药在某一直径d下实验,提高装药密度而使炸药熄爆(“压死”),则可以看成是炸药达到了该密度下的临界直径d而发生了熄爆。同样也是由于孔隙搅拌混合作用减弱,使化学反应区增厚的结果。早期对TNT炸药的临界直径的研究也发现,高密度的TNT临界直径也较大[66]。可见高密度“压死”现象是对于依靠孔隙敏化点火的炸药是一个共性,高密度“压死”直接对应着炸药的临界直径,也与炸药极限直径成正比。
5 结语
1)在工业炸药爆轰过程中,大量微孔隙高速塌缩起到 “热点”点火、混合搅拌和湍流耗散热释能三重作用。其“热点”是孔内气体的绝热压缩、射流冲击、摩擦剪切作用的结果。冲击射流继续发展成为起搅拌作用的旋涡、涡环,促进氧化剂与还原剂之间的物质传递与扩散,进而增强了化学反应。微漩涡和微冲击波的湍流能量再通过粘性耗散转变为热能支持爆轰波。
2)工业炸药的孔隙塌缩湍流对爆轰化学反应起促进作用,但其本身的耗散减慢则消耗爆轰波能量。所以维持爆轰波传递的能量包含了化学能和湍流耗散热两个部分,爆轰波厚度不仅只是化学“反应区”的贡献,而是包含由“反应区”和“湍流耗散”共同组成的爆轰波“释能区”。
3)爆轰波总释能区宽度由化学反应区和湍流区的最大值构成。随着装药密度的变化,释能区存在一个最小厚度,此即能量利用率最高的最佳装药密度。
4)高密度“压死”现象是依靠孔隙敏化点火的混合炸药的共性,是该类炸药维持爆轰的总“释能区”增厚的结果,高密度“压死”直接对应着炸药的临界直径,也与炸药极限直径成正比。
5)起敏化作用的孔隙尺寸需与炸药粒径相匹配,其量级应取炸药粒径1~10倍为宜。对于粒径约5~6 μm乳化炸药,直径小于1 μm的孔隙对氧化剂和还原剂的混合作用较小,0.1 μm量级的孔隙基本上只能作用于氧化剂或还原剂的单相,混合作用和热点作用都不大。综合考虑热点、混合和旋涡耗散作用,敏化孔径在10~100 μm量级为最佳。

