卡方检验在IBDP生物教学中的应用与启示
曾 弦
(深圳市高级中学 广东深圳 518040)
χ2检验在 IBDP(International Baccalaureate Diplo⁃ma Programme)生物教学中主要有两种用途:独立性检验和适合性检验,这两者都适用于离散型数据的假设检验,其基本原理是通过χ2值的大小来检验实际观测值与理论值之间的偏离程度。独立性检验是判断两个或两个以上因素之间是否具有关联关系的假设检验;适合性检验是比较观测值与理论值是否符合的假设检验。下面结合IBDP生物教材中的具体案例来详细说明。
1 独立性检验
独立性检验是研究两个或两个以上因子彼此之间是相互独立还是相互影响的一类统计方法。具体做法是,先提出无效假设(H0),假设所观测的各属性之间没有关联,根据无效假设计算理论数,在一定自由度下以给定的显著性水平做出判断,最后证明无效假设是否成立。若拒绝无效假设(H0),则说明两种因子之间的关联是显著的;若接受无效假设(H0),则说明两种因子之间无关联,是相互独立的。独立性检验的形式有多种,常利用列联表进行检验,在生物学研究中常用2×2列联表。在IBDP生物中独立性检验主要应用于“生态学”这一章,用来检验两个物种的分布是否具有关联性。
以2014年牛津大学出版社出版的IB Diploma Programme:Biology中第四章“生态学”中课后习题为例详细说明。
英国什罗普郡某山顶上的草地,这个地区在夏天有绵羊在此放牧,此外还有登山者在草地上穿过。草地上有凸起的小丘,上面长着石楠(Calluna vulgaris)。对该处的肉眼观察发现,有一种苔藓(Rhytidiadelphus squarrosus)与这种石楠有关。随机调查统计了100个样方的数据,两个物种的分布情况见表1。这两个物种的分布是否具有关联性?
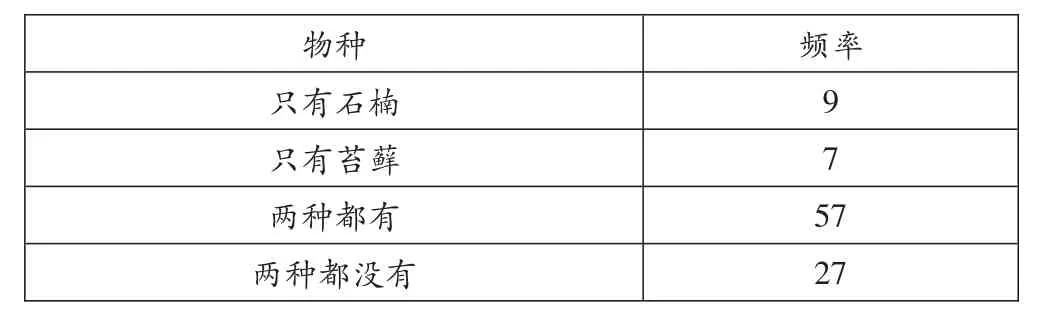
表1 两个物种的分布
解题步骤如下:
(1)构建一个观察值的列联表:基于已知数据构建一个2×2列联表,即横行分为两组数据,纵列也分为两组数据(表2)。

表2 根据表1所构建的列联表
(2)假设两个物种的分布没有关联,计算理论值(理论值=行总和×列总和/总数)。理论值的结果见表3。

表3 理论值的计算结果
(3)确定自由度:自由度有公式,df=(m-1)(n-1),m是行数,n是列数。在生物学研究中常用2×2列联表,故自由度常等于1。本题中自由度=(2-1)(2-1)=1。
(4)确定临界值:要确定一个否定无效假设(H0)的概率标准,这个概率标准叫做显著性水平或者概率水平,记做α。α是人为规定的小概率界限,生物学研究中常取α=0.05和α=0.01两个显著水平,IBDP生物中常取α=0.05。
查χ2值表(常见用表)可以看出,α=0.05,df=1时,临界值为3.84。
(5)计算本题中的χ2值。
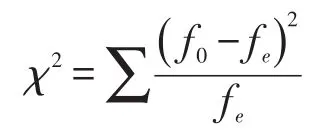
其中,f0表示观察频率;fe表示理论频率。χ2=(57-42.2)2/42.2+(7-21.8)2/21.8+(9-23.8)2/23.8+(27-12.2)2/12.2=5.190 5+10.047 7+9.203 4+17.954 1=42.395 7。
(6)陈述无效假设H0和备择假设H1,并使用卡方检验的计算值对其进行评估:无效假设H0:石楠和苔藓的分布是相互独立的;备择假设H1:石楠和苔藓的分布是有显著关联的。
计算出的卡方值42.395 7大于临界值3.84,有证据表明这两个物种之间存在5%的关联,即可以拒绝无效假设H0,接受假设H1,即石楠和苔藓的分布是有显著关联的。
如计算出的卡方值小于或者等于临界值3.84,则不能拒绝无效假设H0。没有证据表明这两个物种之间有5%的关联,即石楠和苔藓的分布是相互独立的。
2 适合性检验
比较观测值与理论值是否符合的假设检验叫适合性检验。这种方法是先对样本的理论值通过一定的理论分布推算出来,再用实际观察值与理论值比较,从而得出实际观测值与理论值之间是否吻合的结论。在IBDP生物中适合性检验主要应用于遗传学这一章,用来检测所得的结果是否符合孟德尔分离定律、自由组合定律等。
做适合性检验时,可以先提出无效假设H0:O-E=0,即观察值与理论值之间没有差异,再计算样本的卡方值χ2,根据规定的显著性水平α和自由度df从χ2值表(常见用表)中查出相应的卡方值,如果计算出的卡方值大于查表所得卡方值,则拒绝无效假设H0,如果计算出的卡方值小于查表所得卡方值,则接受无效假设H0。
以2014年剑桥大学出版社出版的Biology for the IB Diploma中第十章“遗传学”中课后习题为例详细说明。
例:孟德尔单因子杂交实验。有人种植了7 324株豌豆,在这一代中,他观察到5 474株黄色种子植物和1 850株绿色种子植物。这一实际观察值是否符合孟德尔一对等位基因的遗传规律,即黄色种子∶绿色种子=3∶1?
本例为判断实际观察值与理论比率是否相符的问题,属于典型的适合性检验问题。解题步骤如下:
(1)设置无效假设H0:黄色种子与绿色种子符合3∶1的比率。对于一个单因子杂交实验来说,理论的表型比率F1代是3∶1。如果计算7 324株植物,理论上,预期比率(E)将是5 493∶1 831(即3∶1)见表4。
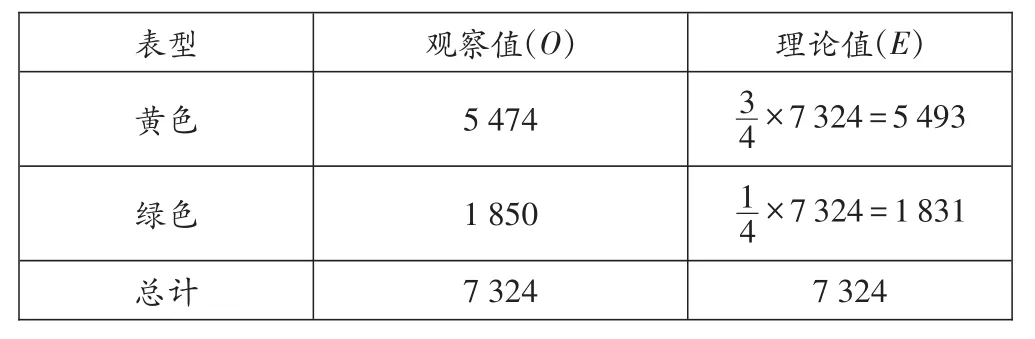
表4 理论值的计算过程
其中,O表示观察值;E表示理论。χ2=(5 474-5 493)2/5 493+(1 850-1 831)2/1 831=0.065+0.197=0.262。
(3)确定自由度:自由度df,即结果中的类别数减去1。此题中只有两种类型(黄色种子和绿色种子),因此自由度df=2-1=1。
(4)找到自由度是1,显著性水平为5%(0.05时)的临界卡方值,将计算出的卡方值与查表值比较。如果计算出的卡方值大于这个值意味着拒绝无效假设H0,即不符合3∶1的分离比;如果计算出的卡方值小于这个值意味着接受无效假设H0,即符合3∶1的分离比。在本题中计算出的卡方值是0.262,查表所得卡方值是3.841,0.262小于3.841,因此接受接受无效假设H0,假设观察到的结果和预期结果之间没有显著差异,即结果符合3∶1的预期分离比。
3 启示
生物学是一门实验学科,实验数据的分析和处理是非常重要的研究手段。我国高中生物学课程标准中没有对生物数据的统计以及掌握程度做明确规定,教材中也没有单独设置的章节加以介绍,各类考试评价中也未有相关要求。学生在高中生物实验中获得数据,仅进行记录和简单的处理即可,没有利用统计学的手段来对实验数据进行系统分析。生物统计学相关的内容在我国往往被放在大学生物学专业讲述。
IBDP生物学对实验数据的处理有较高的要求,2011年IBDP生物学大纲第一部分就是统计分析,明确学生必须掌握平均数、标准差、正态分布以及如何表示数据测量的误差,并且能用统计学的方法进行数据处理,如用t检验来判断数据间平均值之间是否存在显著性差异,又或者偶然因素导致。2016年新修订的IBDP生物学大纲另外增加了卡方检验的内容。这些足见IBDP生物对数据处理的重视程度,也显示了实验科学在自然科学学科中的重要地位,这种能力的培养对于学生阅读生物学文献以及处理生物学实验数据是非常重要的。IBDP生物学作为一门实验学科,注重实验数据的规范表达和生物统计方法的应用,这些应是我国高中生物课程的借鉴之处。

