基于DNN 网络结构的学院转专业生源研究

高 实

(吉林省教育学院 国培项目执行办公室,长春 130022)

0 引 言

转专业是大学生在上大学后面临的关键问题[1]。在统计参与转专业的学生总人数后,往往会由于难以预测热门学院的报名人数而导致后续的工作难以开展,从而使转专业的相关制度难以完善[2]。

针对现有的预测方法只能定性分析转专业的学生去向,难以定量分析为后续转专业的相关工作提供数据支撑,为此笔者提出了DNN(Deep Neural Network)网络架构并结合吉林大学近十五年热门学院的转专业报名情况,在Tensorflow 框架下训练DNN 模型,为随机现象的建模和转专业的后续工作分析提供了有效的工具。

DNN 网络[3]是深度学习的重要网络架构,作为大量的数据分析及推理的有效工具,DNN 网络能在保持模型精确性的条件下,有效减少及避免由普通感知机网络所带来的梯度爆炸,过拟合等问题的影响,其实用性强,结构明了,在实际数据分析模型中得到广泛应用。

针对热门学院转专业报名人数的定量预测分析,其中的不确定性因素影响较大,通过已有数据,训练计算DNN 网络,可以较为容易地建立预测模型,省去考虑不确定性因素的步骤,因此,笔者以吉林大学热门学院转专业报名历史数据为基础,首先从DNN 网路入手,在谷歌的Tensorflow 框架上搭建网络并选择合适的优化器训练网络,进一步通过2008-2017 学年的转专业历史数据训练优化网络权值与偏置,预测在未来已知参与转专业总人数的条件下,报名热门学院的学生人数,为转专业的后续相关工作提供数据支持,且随着时间推移,已知数据越来越来丰富,可以进一步训练网络,以提升DNN 架构的预测精度,进一步推进转专业的相关工作开展。

1 基于DNN 网络热门学院报名预测模型的建立

首先建立DNN 网络模型[4-5],为热门学院报名预测提供理论基础。

1.1 DNN 网络原理

1.1.1 网络基本单元

DNN 网络由多个神经元构成,如图1 所示,以单个神经元模型(也称为感知机模型[6])为例,假设它有若干个输入和一个输出。

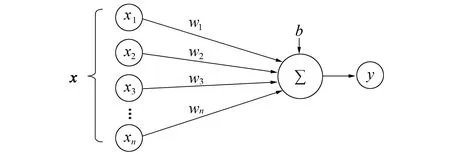
图1 单个神经元线性模型Fig.1 Single neuron linear model

中间输出结果为

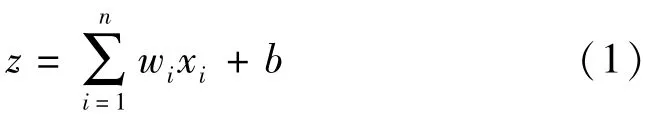
激活函数得到神经元输出为

因此对一个基本神经单元的计算分为两个步骤。首先是权重、偏置与输入的线性计算得到中间结果,再通过激活函数求得神经元最终的输出。

1.1.2 网络模型的搭建

从DNN 按不同层的位置划分,DNN 内部的神经网络层可分为3 类:输入层,隐藏层和输出层[6](见图2)。第1 层是输入层(Input Layer),最后一层是输出层(Output Layer),而中间的层数都是隐藏层(Hidden Layer)。因此对DNN 网络,其隐藏层可以有多层,层与层之间是全连接的,即第i层的任意一个神经元一定与第i+1 层的任意一个神经元相连。虽然DNN 看起来很复杂,但对小的局部模型,还是和上述的感知机模型相同,即一个中间结果加上一个激活函数factive(z)。

图2 DNN 网络模型Fig.2 DNN network model

1.2 DNN 网络常用激活函数[7]

1.2.1 Sigmod 函数

Sigmod 是常用的非线性的激活函数,其数学形式如下

Sigmod 几何图像如图3 所示。其一个优良特性就是能将z∊R的输入压缩到z∊(0,1)区间,这个区间的数值在神经网络中常用于将网络的中间结果转换为概率分布(0,1)区间的输出,即用于解决2 分类问题。

图3 Sigmod 函数曲线Fig.3 Sigmod function curve

1.2.2 ReLu 函数

为避免使用Sigmod 而出现的梯度弥散现象(即网络参数长时间得不到更新,导致训练不收敛或停滞不动的现象发生),引入ReLu 激活函数(见图4)能很好地避免这一情况发生,ReLu 函数定义为

图4 ReLu 函数曲线Fig.4 ReLu function curve

对输出结果为某段或整个实数空间,例如房价预测、函数趋势预测等问题,常用ReLu 函数作为激活函数。

1.3 基于Adam 梯度下降的参数优化方法

假设网络预测输出为Vi,而实际数据值为Mi,则不可避免地预测输出与实际数据会有损失loss,在回归预测问题中,损失函数常用均方差定义如下

其中规定β1=0.9,β2=0.999,ε=10-8,w为迭代更新的数值,v,s为在梯度更新过程中的中间变量。Adam 算法相当于先把原始梯度做一个指数加权平均,再做一次归一化处理,然后再更新梯度值。应用此方法可以同时更新网络的权值与偏置。

1.4 数据预测

在谷歌开发的Tensorflow 框架下进行DNN 网络的训练,针对问题类型选择激活函数,回归问题对应ReLu 激活函数；分类问题对应Sigmod 激活函数或Softmax 激活函数。将收集到的数据输入到网络中,应用Adam 梯度下降算法更新网络权值,直到损失函数值达足够小后,网络训练完成,可以预测未来的热门学院报名人数。

2 基于DNN 神经网络的热门学院转专业报名人数预测

2.1 训练数据

如图5、图6 所示,以2008-2017 年的数据作为DNN 网络训练数据,可以看出,对热门学院,随着年份推移,热门学院会更加热门,热门学院的转专业报名人数也随报名转专业的总人数变化而改变。因此,将网络的输入特征定义为年份与每年的报名转专业总人数,针对吉林大学转专业现状,DNN 网络对应的特征输出就是报名临床学院、法学院以及汽车工程这3 个热门学院转专业的人数。

图5 吉林大学2008-2019 年热门 学院转专业报名人数Fig.5 The number of applicants for changing majors in popular colleges of Jilin University from 2008 to 2019

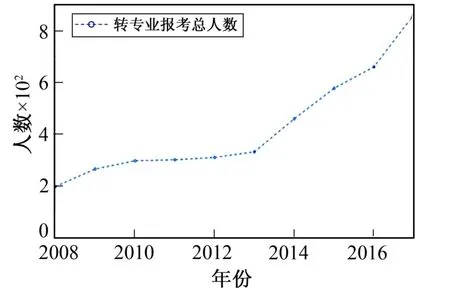
图6 吉林大学2008-2017 年参与 转专业学生总数Fig.6 Total number of students who changed majors in Jilin University from 2008 to 2017

2.2 DNN 网络建立

由数据可知,其特征为年份和报名转专业的总人数,特征输出为报名3 个热门学院转专业的人数。因此,得到DNN 网络的输入层为2 个神经元,输出层为3 个神经元。设置中间隐藏层为2 层。如图7 所示。其中隐藏层的第1 层设置为6 个神经元,第2 层设置为4 个神经元。

图7 转专业人数预测DNN 网络Fig.7 DNN Network for torecast of the number of professionals transfemed

2.3 网络激活函数选择与梯度优化

对热门学院转专业报考人数进行预测问题,可以归结于回归类问题,因此选择激活函数为ReLu,应用Adam 梯度下降算法对网络权值、偏置进行更新。

2.4 多损失函数定义

利用Tensorflow的多线程模式,开启3 个会话,利用Adam 梯度下降方法,使以上3 个损失函数同步达到极小值,完成网络训练。

3 仿真结果

3.1 DNN 网络验证与预测

3.1.1 DNN 网络验证

将2017 年的数据作为验证集,2008-2016 年的数据作为训练集,将训练数据的特征作为验证输入到训练好的网络中,得到验证输出,与实际结果对比如表1所示,可以看出网络的输出精度很高,训练已经达到目标损失值。

表1 验证结果Tab.1 Verification result

3.1.2 DNN 网络预测

通过网络预测2008-2017 年热门学院转专业报名人数如图8 所示。

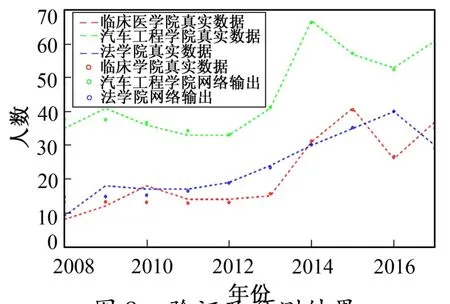
图8 验证及预测结果Fig.8 Verification and prediction results

可以看出网络输出数据与训练集数据基本相符,网络训练效果较好。因此,可以用于对2020 年的热门学院转专业报考人数进行预测。

首先通过对2008-2017 年的转专业报名总人数进行回归预测,可以得到2020 年的预测转专业报名总人数为920 人。然后得到2020 年热门学院转专业报考预测结果(如表2 所示)。

表2 2020 年热门学院转专业报考预测结果Tab.2 Forecast results of popular colleges changing majors to apply for the examination in 2020

4 结 语

通过DNN 网络的验证输出与实际数据值,结果表明网络精度较高,可以满足预测吉林大学2020 年热门学院转专业报考人数的需要,而且随着时间推移,已有数据增多,可以将训练样本增多,重新训练网络权值,以实现精度更高的预测。