基于BAS 优化PNN 网络的电机轴承故障诊断方法

刘 霞 王鑫宇 路敬祎 李其浩

(东北石油大学 电气信息工程学院,黑龙江 大庆 163318)

0 引 言

电机作为工业生产的动力来源,其安全可靠运行是生产的前提。在电机的故障种类中,轴承故障占所有电机故障的40%以上[1]。电机轴承在内圈、外圈、滚动体上易产生裂纹、疲劳剥离等故障[2],其运行状态直接影响电机的工作精度和效率,严重时会发生灾难性的事故。因此对轴承故障诊断的研究具有重要意义。

轴承故障诊断主要分为故障信号获取、特征提取和模式识别3 部分。主成分分析(Principal Component Analysis)和线性判别分析(Linear Discriminant Analysis)是最为经典的特征提取算法[3-4],但这2 种方法由于轴承振动信号的非线性、非平稳性会导致部分非线性特征参数丢失。局部线性嵌入(LLE:Locally Linear Embedding)是一种非线性的特征提取方法,实现了局部邻域的优化选取,提取出最优的敏感故障特征[5]。近年来,许多科研人员将神经网络、智能算法等广泛应用于轴承故障诊断研究。李嫄源等[6]利用粒子群算法(PSO:Particle Swarm Optimization)优化支持向量机(SVM:Support Vector Machine)的惩罚参数和径向基核函数参数,提高故障识别率。多层前馈神经网络(BPNN:Back Propagation Neural Network)在轴承诊断中已取得成熟应用,但存在学习收敛速度慢、易陷入局部最小点等问题[7]。唐立力等[8]利用思维进化算法优化BP 网络中的权值和阈值,解决了该问题并提高了故障诊断准确度。

概率神经网络(PNN:Probabilistic Neural Network)是一种完全前向的计算过程,不需要进行反向误差计算,弥补了BP 神经网络的不足,且具有学习速度快,噪声容忍度高等特点,适合解决模式分类等问题[9-11]。但PNN 网络分类的准确性取决于参数平滑系数δ的设定。笔者提出了一种天牛须搜索算法优化概率神经网络参数的轴承故障诊断模型,利用天牛须搜索算法优化PNN 模型中的平滑系数δ,避免了人为因素的影响,并提高了模型的自适应能力和容错能力。实验结果表明该方法能有效地对电机轴承故障进行诊断,且准确率较高。

1 概率神经网络

概率神经网络是基于贝叶斯策略前馈神经网络,PNN 网络由输入层、模式层、求和层和输出层组成[12-13],如图1 所示。

图1 PNN 网络结构Fig.1 PNN block diagram

输入层将输入样本传递给模式层,神经元的个数等于特征向量的维数。模式层主要计算各样本类别的概率,各模式单元有相同的输入,模式单元个数等于训练样本数,该层每个模式单元的输出为

其中X为输入的特征向量；Wi为两层之间的权值；δ为平滑系数,是决定分类效果的关键参数。

求和层与模式层的各单元相连,对其各类别的输出进行加权平均。输出层根据上层对各模式的概率估计,采用Bayes 分类规则,选取最大后验概率的神经元作为系统输出,具有概率密度函数最大的神经元输出为1,其他神经元的输出全为0[14]。

PNN 网络根据学习样本和期望值可以直接获得网络隐层单元的连接权值,不易收敛于局部最小,故不需要反复重新训练网络[15]。但PNN 模型中根据人为经验设置的平滑系数δ,不能完整的表达出输入样本的概率特性。因此,PNN 模型的关键在于确定合适的平滑系数δ[16]。

2 天牛须搜索算法

天牛须搜索算法(BAS:Beetle Antennae Search)于2017 年由天牛觅食原理衍生得到的全局寻优智能优化算法,在不具备具体形式和梯度信息的条件下,能快速收敛、高效寻优[17]。

根据BAS 算法的仿生学思想,对未知区域采用随机搜索的方式。首先利用

产生一个随机方向α模拟这种行为。其中rands()为随机向量且产生的数在[-1,1],l为空间维度。天牛两个触角的空间坐标为

其中xl为天牛左须的位置坐标,xr为天牛右须的位置坐标；xm为天牛的位置坐标；dm为左右两触角的距离。计算左右两个触角感受到的食物气味强度,分别用fleft=f(xl),fright=f(xr)表示,其中f(x)为适应度函数。然后天牛利用

对位置进行更新。其中δm为搜索步长；sign()为符号函数。

当到达迭代次数时,天牛位置停止更新。笔者利用

对搜索步长δm和距离dm进行更新,其中c1、c2为预先设定的常数。

BAS 算法利用食物气味信号强度作为评判标准,即适应度函数值。将天牛头部作为质心,其位置坐标为优化的参数值,通过比较天牛两个触角感受到的食物气味强度,使天牛向气味强烈的触角方向移动一个步长,从而更新天牛的位置坐标。将步长设置为随迭代次数增加而减小的变步长,可使适应度函数快速收敛,使天牛快速到达最终位置并获得食物。

3 基于BAS 优化PNN的诊断方法

笔者将模型分类后测试样本的错误率作为适应度函数,将BAS 优化算法与PNN 模型相结合,根据输入样本的特性确定最后天牛的位置坐标,即平滑系数δ；该方法可以避免人为取值的经验性并且提高PNN 识别特性。为进一步提高BAS-PNN 模型分类的准确性和快速性,并保证充分描述电机轴承的运行状态,不致信息丢失,提取轴承振动信号的时域和频域统计特征参数各15 个,构建高维特征参数矩阵,将经LLE 算法得到的敏感特征参数矩阵作为BAS-PNN 模型的输入样本。利用BAS 算法针对训练样本信号特性确定合适的平滑参数,再对轴承故障信号进行分类,可使模型更加有针对性,提高故障分类准确性。BAS-PNN 轴承故障诊断流程如图2 所示。

图2 BAS-PNN 故障诊断流程图Fig.2 Flow chart of fault diagnosis for BAS-PNN model

4 实验分析

实验数据取自实验室中QPZZ-Ⅱ型故障诊断试验平台,轴承为N205 型,转速为1 150 r/min,采样频率为10 kHz。截取无负载情况下正常状态、滚动体故障、内圈故障和外圈故障4 种状态各100 组,每组样本长度为1 024。分别计算每组数据的15 个时域统计特征参数和15 个频域统计特征参数组成高维特征参数矩阵。利用LLE 算法构造低维敏感特征参数矩阵,设置算法近邻点个数为13,维数为4,即选择4 个敏感特征。将敏感参数矩阵中每种状态(1～80)×4 组作为训练样本,(81～100)×4 组作为测试样本用于验证模型的准确度。轴承样本数据分布如表1 所示。

表1 轴承样本数据分布Tab.1 Bearing sample data distribution

图3 为BAS 算法优化过程曲线图,当优化到第5 代时达到局部最优,最小值为0.062 5,此时平滑系数δ为0.271,测试样本正确率为93.75%。图4 为BAS-PNN 网络的测试结果。

图3 参数寻优过程图Fig.3 BAS optimization process

图4 BAS-PNN 测试结果图Fig.4 Test results of BAS-PNN

为验证所提模型的故障诊断效果,利用其他传统故障分类方法进行比较,均采用相同的数据集,经SVM 得到的测试结果如图5 所示,经BP 网络得到的测试结果如图6 所示,经平滑系数δ=1的PNN 网络得到的测试结果如图7 所示,各方法的对比结果如表2 所示。

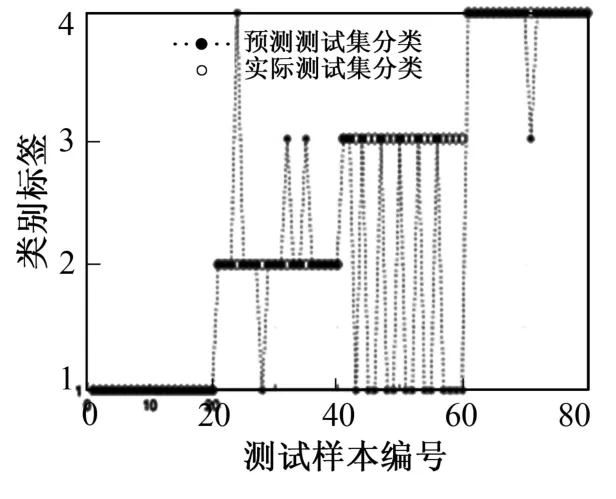
图5 SVM 测试结果图Fig.5 Test results of SVM

图6 BP 网络测试结果图Fig.6 Test results of BP

图7 PNN 网络测试结果图Fig.7 Test results of PNN

表2 轴承故障诊断结果分析Tab.2 Analysis of bearing fault diagnosis results

由表2 可知,测试样本经SVM 分类的准确率为77.5%,经BP 网络分类的准确率为78.75%,经平滑系数δ为1的PNN 网络分类准确率为78.75%。通过对比实验可以得出,笔者提出的BAS 优化PNN网络的方法在分类准确率上优于传统分类方法。耗时方面,该方法是通过BAS 算法根据样本特性确定平滑系数,计算量偏大,会在速度上不如其他传统方法。

5 结 语

由于平滑系数δ是PNN 网络分类的关键参数,笔者提出了一种天牛须搜索算法与概率神经网络相结合的方法,利用BAS 算法对平滑系数进行优化,结合样本特性得到更加合适的数值,避免了人为设置参数对分类结果的影响。利用实验室轴承数据进行验证,得到该方法的分类准确率为93.75%。为进一步说明笔者方法的优势,利用SVM、BP 网络和传统PNN 网络方法进行对比试验,得到的分类准确率分别为77.5%、78.75%和78.75%,证明了笔者方法具有更高的诊断精度。