A STABILITY PROBLEM FOR THE 3D MAGNETOHYDRODYNAMIC EQUATIONS NEAR EQUILIBRIUM∗

(可雪丽) (原保全) (肖亚敏)

School of Mathematics and Information Science,Henan Polytechnic University,Henan 454000,China E-mail:kexueli123@126.com;bqyuan@hpu.edu.cn;ymxiao106@163.com

Abstract This paper is concerned with a stability problem on perturbations near a physically important steady state solution of the 3D MHD system.We obtain three major results.The first assesses the existence of global solutions with small initial data.Second,we derive the temporal decay estimate of the solution in the L2-norm,where to prove the result,we need to overcome the difficulty caused by the presence of linear terms from perturbation.Finally,the decay rate in L2space for higher order derivatives of the solution is established.

Key words Background magnetic field;MHD equations with perturbation;stability;decay rate

1 Introduction

The 3D incompressible magnetohydrodynamic equations can be written as

where

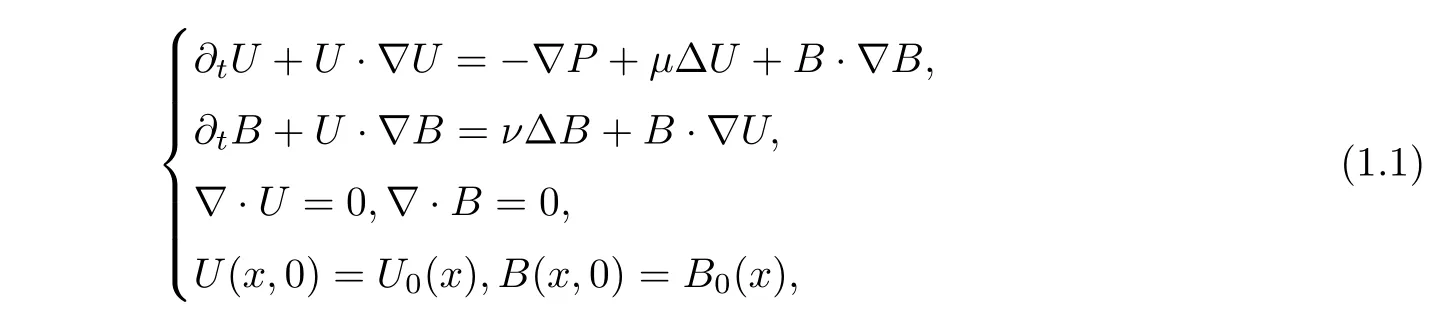
x

∈Rand

t>

0.

U

=

U

(

x,t

)represents the fluid velocity,

B

=

B

(

x,t

)the magnetic field,and

P

=

P

(

x,t

)the pressure.For simplicity,we set the viscosity coefficient

µ

and the magnetic field coefficient

ν

to 1.The MHD equations(1.1)involve the coupling of the incompressible Navier-Stokes equation and Maxwell’s equation.They play an important role in many fields,such as geophysics,astrophysics,cosmology and engineering(see[3,5,19]).Because of the physical and engineering applications of MHD equations,the mathematical study of them is very important;as a result,the MHD equations have been extensively studied.For instance,G.Duvaut and J.L.Lions[8]obtained the local existence and uniqueness of a solution in the Sobolev space

H

(R)

,s>d,

and proved the global existence of the solution for small initial data.M.Sermange and R.Teman[25]further studied the properties of the solutions.Miao,Yuan and Zhang[18]studied the well-posedness of solutions of MHD equations in BMO(R)and

bmo

(R),and proved that the solution of the Cauchy problem of MHD with small initial value is globally unique in BMO(R)and locally unique in

bmo

(R).Cao,Wu and Yuan[4]studied the 2D incompressible MHD with partial dissipation for data in

H

(R)

,s>

2.Recently,the global regularity issue concerning equations(1.1)has attracted much interest,and considerable results have been obtained(see[9,11,29]).For the 3D equations around the equilibrium state(

U

,B

),it is clear that

U

(

x,t

)=(0

,

0

,

0)and

B

=(1

,

0

,

0)are the special solutions of(1.1).The perturbation(

u,b

)around this equilibrium with

u

≜

U

−

U

,b

≜

B

−

B

obeys

where

x

∈R,

t>

0.

In this paper,inspired by references[23,30],we study the global solutions and decay estimates to equations(1.2)in

H

(R).For the global solution of equations(1.2),we refer to[16,27].For the decay estimation of equations(1.2),we refer to[7,15,21,24].However,the classical method does not apply here,due to the appearance of linear terms

∂

u

and

∂

b

from the perturbation in equations(1.2).We introduce a diagonalization method to eliminate the linear terms,then we prove the temporal decay estimates by the classical Fourier splitting method.Our main results are stated as follows:

First,to prove the global well-posedness of small initial data in Theorem 1.2,we need the local well-posedness result of the strong solution in Proposition 1.1,which can be obtained by a standard procedure with Friedrichs’method.The key estimate is that

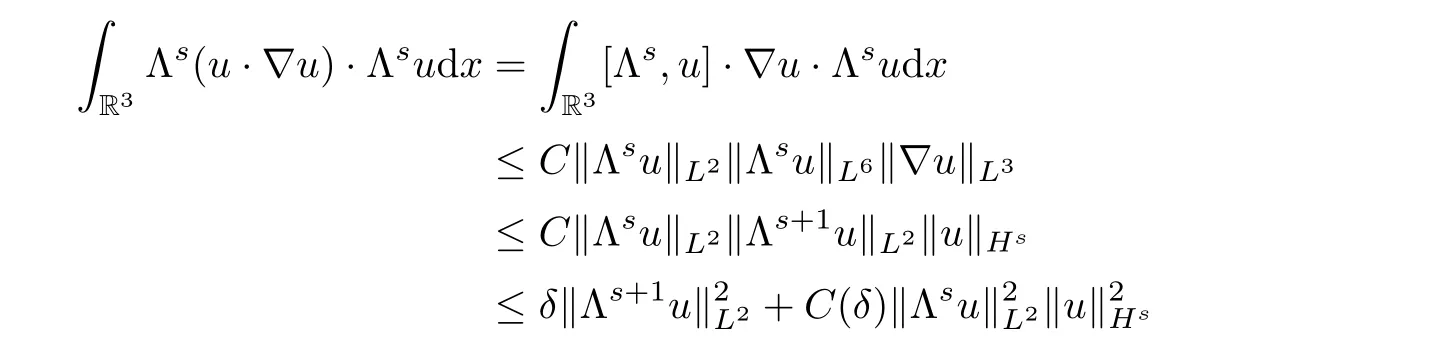
The decay rate of the higher order derivative of the solution is also obtained.

Theorem 1.4

Under the assumption of Theorem 1.3,for any integer

m

≥0,the small global solution(

u,b

)satis fies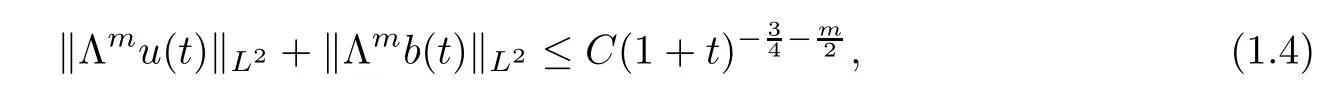

where

C

is a constant which depends on

m

and the initial data.Λ=√−∆is de fined in the end of this section.

Remark 1.5

The decay rates(1.3)and(1.4)are optimal in the sense that they coincide with the ones of the heat equation.

Remark 1.6

For the real number

s>

0,we can also obtain the time decay rate of the

L

−norm for the

s

-order derivative of the solution by the interpolation relation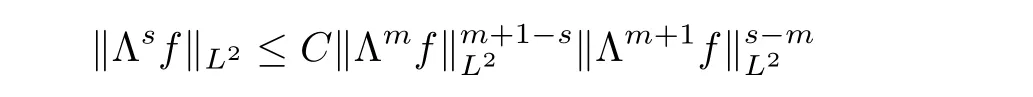

with

m<s<m

+1,which is

2 Preliminaries

The primary purpose of this section is to give three Lemmas;the first one is the product type estimate,the second and the third are mainly used for the decay estimate of a solution.The detailed processes are as follows:

Lemma 2.1

(Product estimate[13,14,17])Let 1

<p<

∞,and

s>

0.Then there exists a constant

C

such that

We will use the following

L

estimate of the Fourier transform of the initial datum in a ball(the proof of Lemma 2.2 is based on the Hausdorff-Young theorem;for more details please refer to[12,22,30]):

Lemma 2.2

Let

u

∈

L

(R),1≤

p<

2.Then

where

S

(

t

)={

ξ

∈R:|

ξ

|≤

g

(

t

)}is a ball with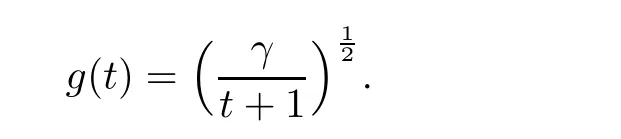

Here,

γ>

0 is a constant which will be determined later,and C is a constant which depends upon

γ

and the

L

norm of

u

.In order to prove Theorem 1.2,we need to calculate the estimates of|

u

︿(

ξ

)|and|︿

b

(

ξ

)|,which will play a key role in this paper.For more details,readers can refer to[7,26].

Lemma 2.3

Letting(

u,b

)∈

C

([0

,T

];

H

(R))be a global solution to the Cauchy problem(1.2)with initial data(

u

,b

)∈

L

(R)∩

H

(R),there exists a constant

C>

0 depending only on‖

u

‖and‖

b

‖such that

Proof

We rewrite(1.2)in the following form:

Here

G

:=−

u

·∇

u

+

b

·∇

b

−∇

p

,

F

:=−

u

·∇

b

+

b

·∇

u.

We take the Fourier transform for(2.3)as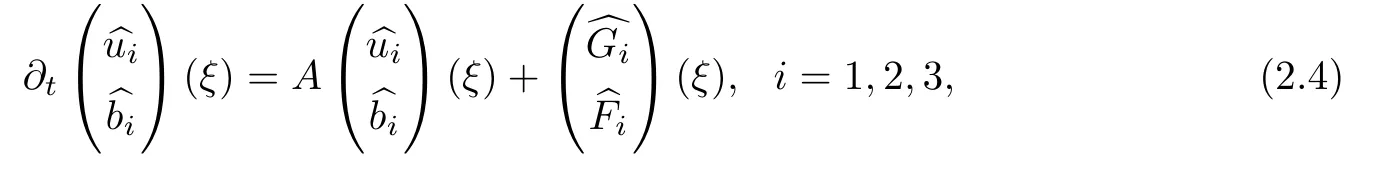

Then the eigenvalues of matrix A can be calculated as follows:

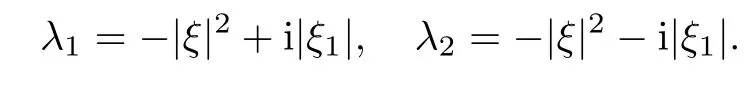
The associated eigenvectors are

The matrix

C

of the eigenvectors and its inverse are given by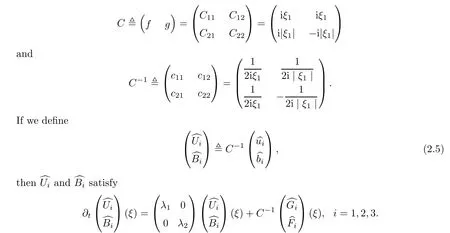

Integrating in time,by Duhamel’s formula,we have

for

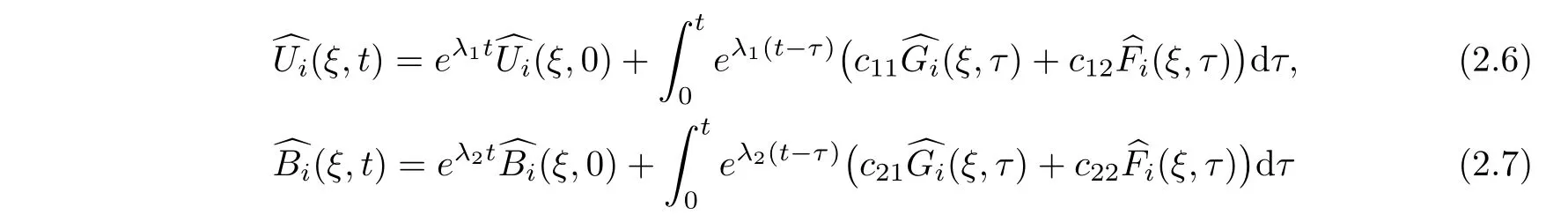
i

=1

,

2

,

3,and,according to(2.5),we have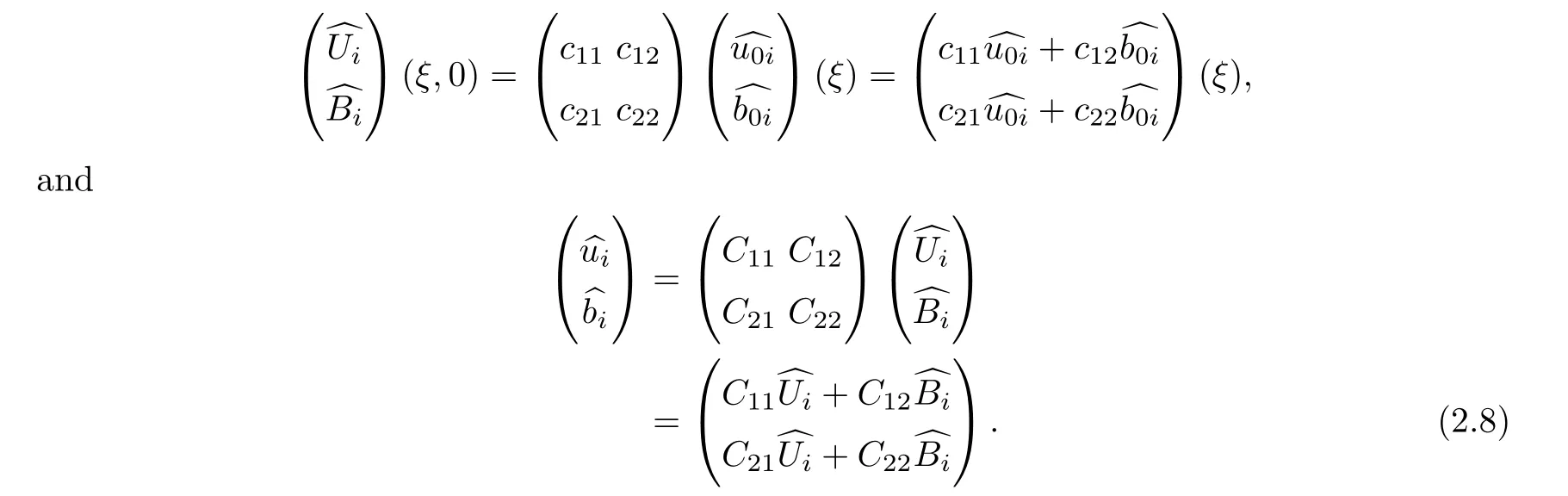

We can get from(2.6)–(2.8)that

Taking the divergence of(1.2),and using the divergence free condition of

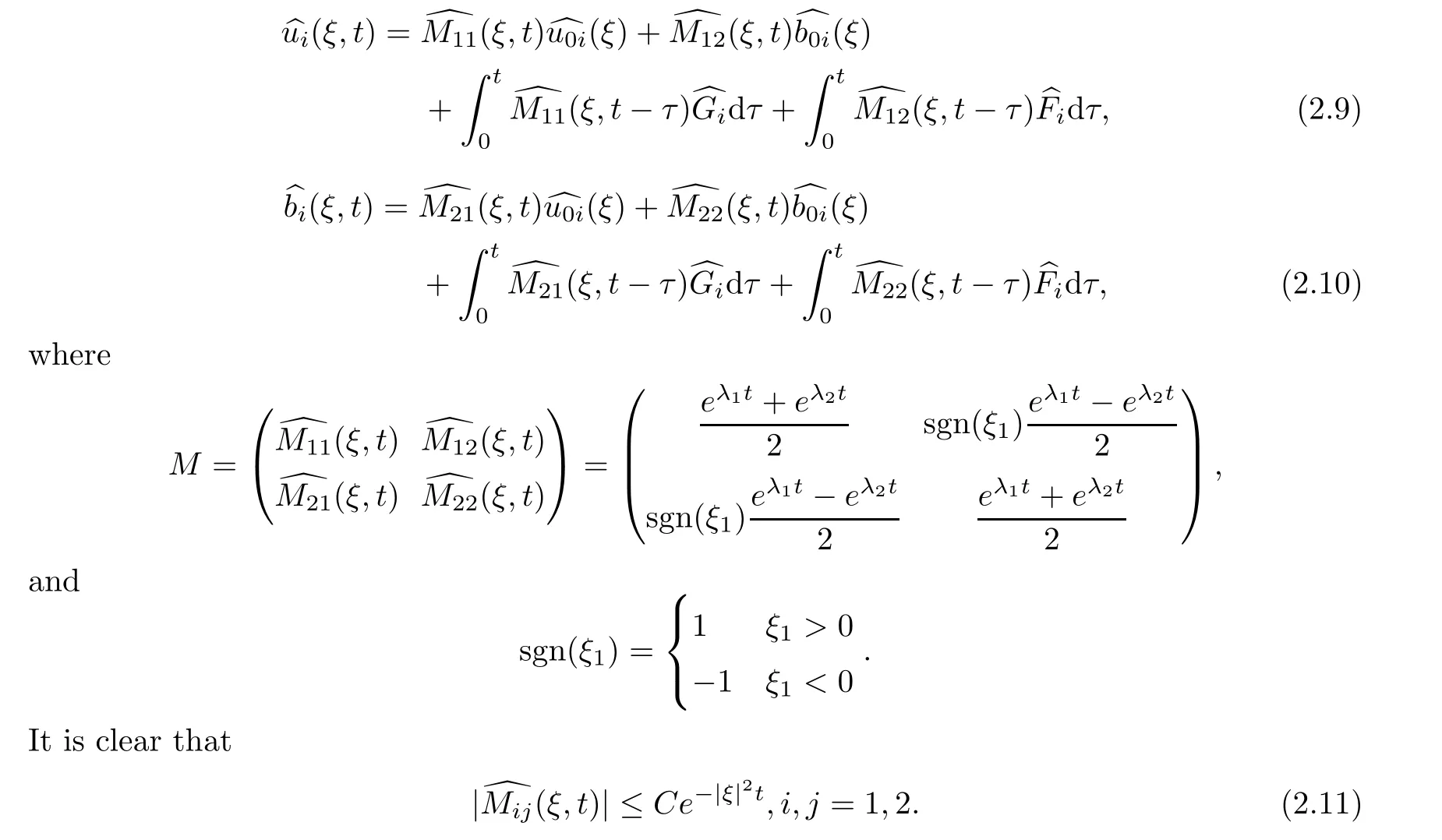
u

and

b

,we have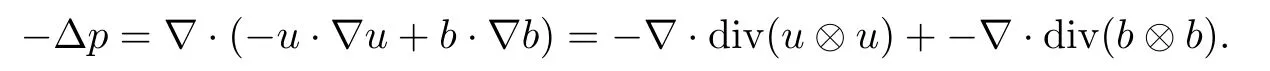

Since the Fourier transform is a bounded map from

L

to

L

,this leads to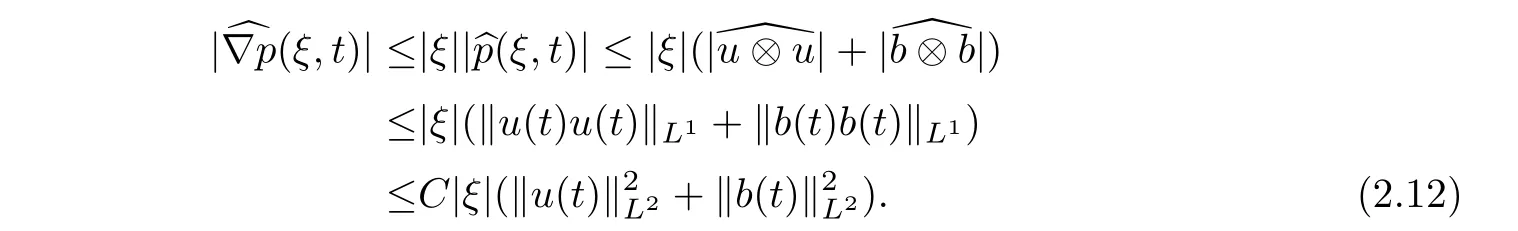

Similarly,by the divergence free condition of

u

and

b

,we can obtain that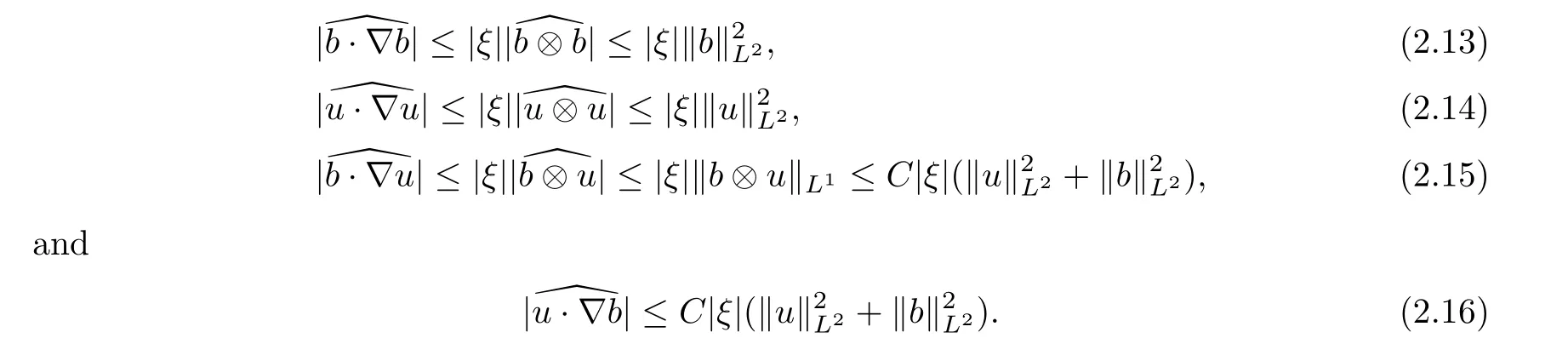

Combining the estimates(2.12)–(2.16),by the expression formula of

G

and

F

,we get

Inserting(2.17),(2.18)and(2.11)into(2.9),we deduce that

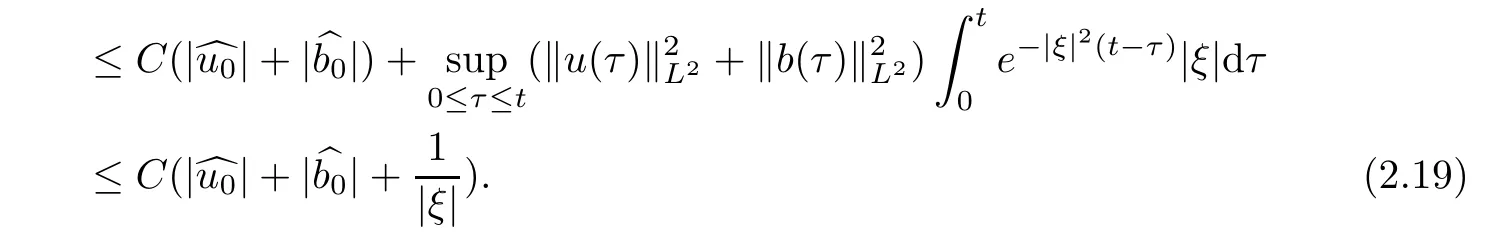
Using an argument similar to(2.10),we have

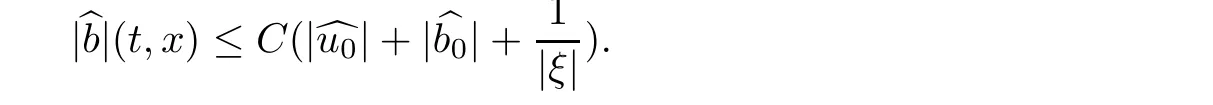
The proof of Lemma 2.3 is thus completed.

3 Proof of Theorem 1.2

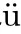
3.1 L2estimate

Taking the

L

inner products of the equations(1

.

2)with

u

and

b

,and adding the results and integrating by parts,we obtain

where we have used the fact that

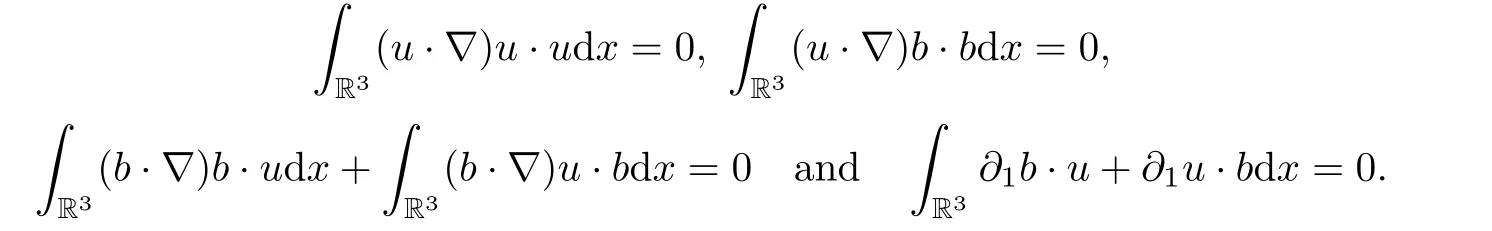
3.2 Hsestimate

Applying Λto the equations of(1.2),dotting the resulting equations with Λ

u

and Λ

b

,and integrating over R,we have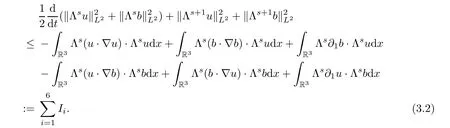

Now,we estimate

I

–

I

.For the term

I

,by the divergence free condition of

u

,integration by parts,Lemma 2.1 and‖

f

‖≤

C

‖

f

‖,we obtain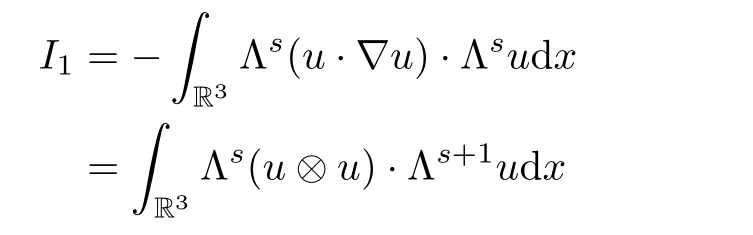

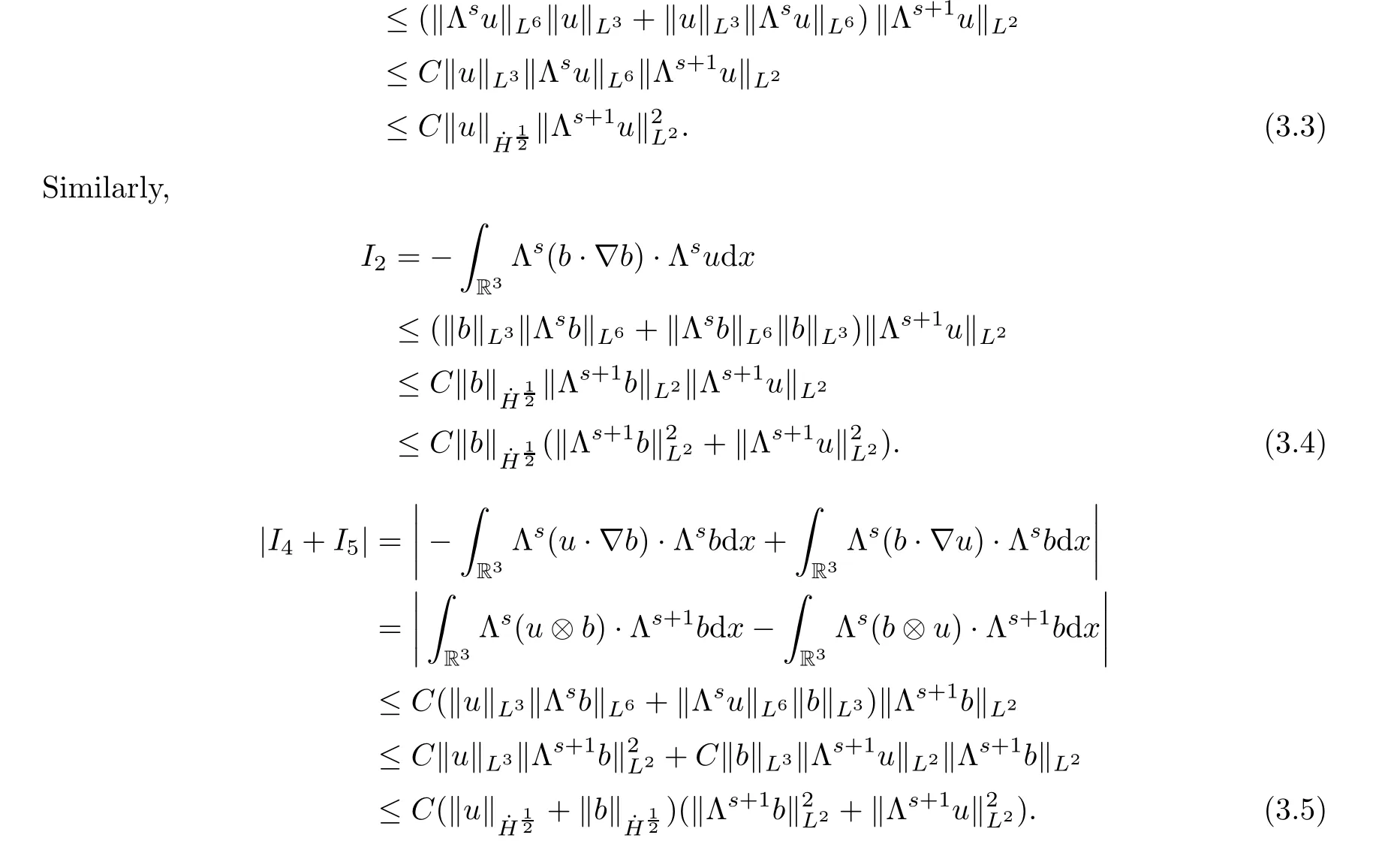
For the terms

I

and

I

,integrating by parts,we get

Combining this with estimate(3.1),we have

Thus,by a continuous extending argument,we get

for all 0

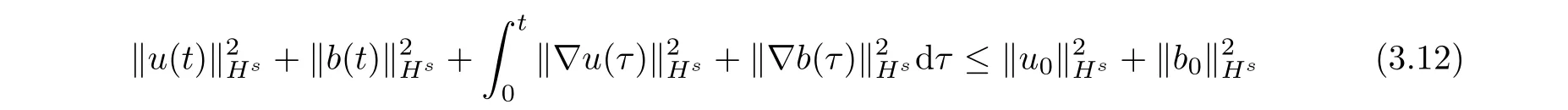
<t<

∞.This completes the proof of Theorem 1.1.

4 Proof of Theorem 1.3

In this section,we prove the decay rate of the global solution in

L

(R)by the classic Fourier splitting method.

Proof

Applying Plancherel’s theorem to(3.1),and by splitting the phase space Rinto two time-dependent parts,we get

where

S

(

t

)and

g

(

t

)are de fined in Lemma 2.2,and

γ>

0 is a constant which will be determined later.Thus,we obtain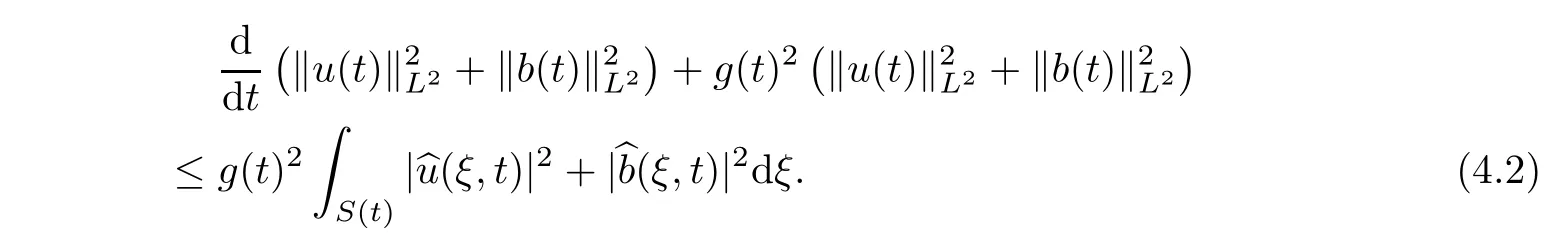

Multiplying(4.2)by the integrating factor(

t

+1),it follows that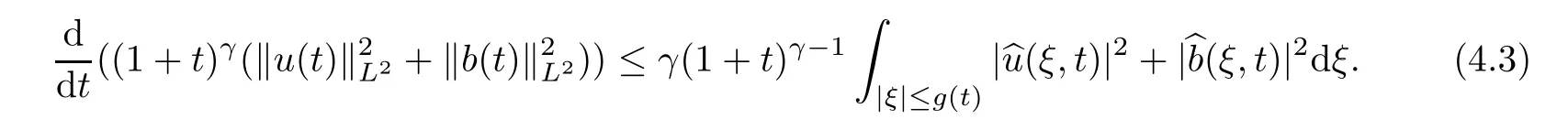

By Lemma 2.3,we have

Integrating(4.4)in time from 0 to

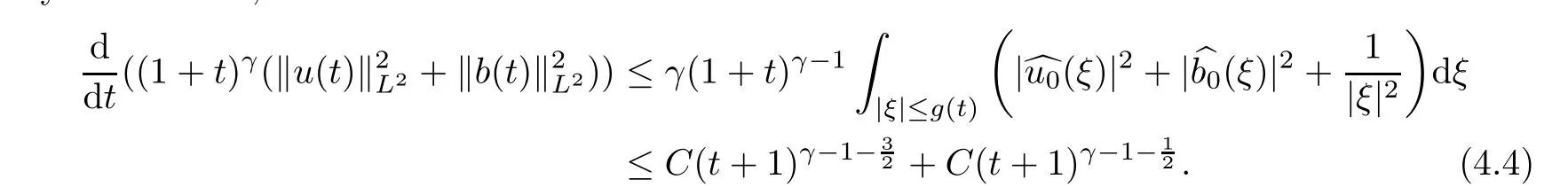
t

leads to the result

Inserting estimate(4.6)into(2.19),we can obtain that in the ball

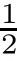
S

(

t

),

Similarly,we obtain

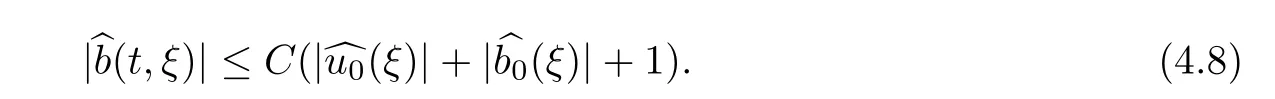
Inserting(4.7)and(4.8)into(4.3),and by Lemma 2.2,we have

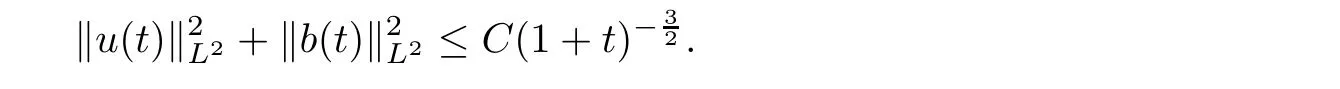
This completes the proof of Theorem 1.2.

5 Proof of Theorem 1.4

In this section,we will prove the higher order derivative’s decay estimate of the small global solution to the equations of(1.2)in

L

(R)space.

Proof

We use the Fourier splitting method again.Let

Then Plancherel’s theorem and(5.1)imply that

where

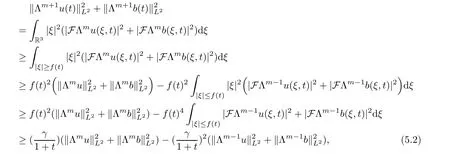
m

≥1 is an integer.Inserting estimate(5.2)into(3.8),it follows that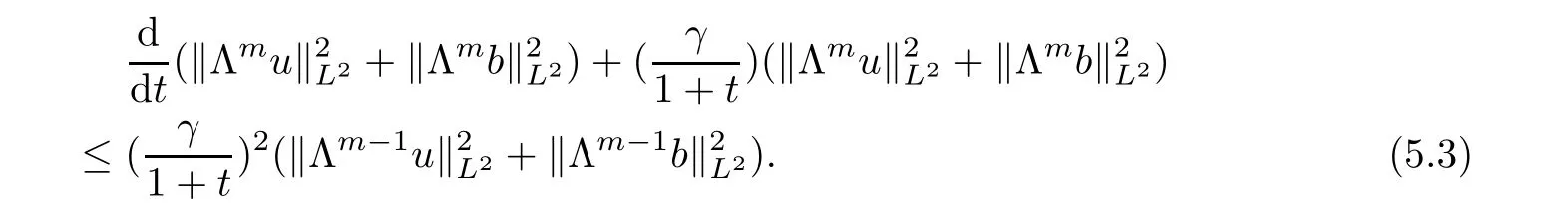

By induction,when

m

=1,multiplying both sides of inequality(5.3)by the integrating factor(

t

+1)yields

Integrating inequality(5.4)from 0 to

t

,we have

Assuming that for

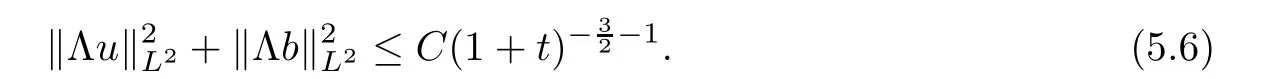
m>

1,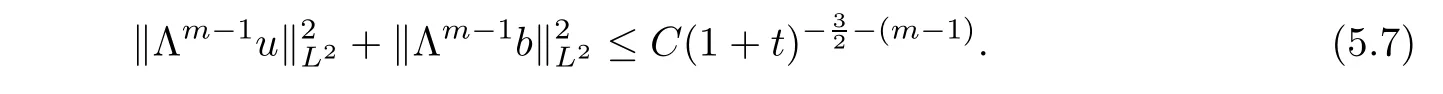

Therefore,inserting the above estimate into(5.3),we have

Multiplying both sides of(5.8)by(1+

t

),we obtain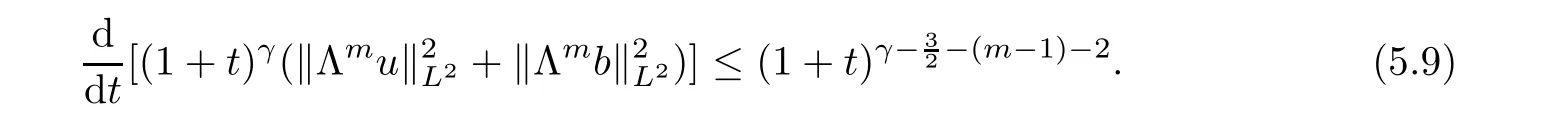

Integrating(5.9)on[0

,t

],we get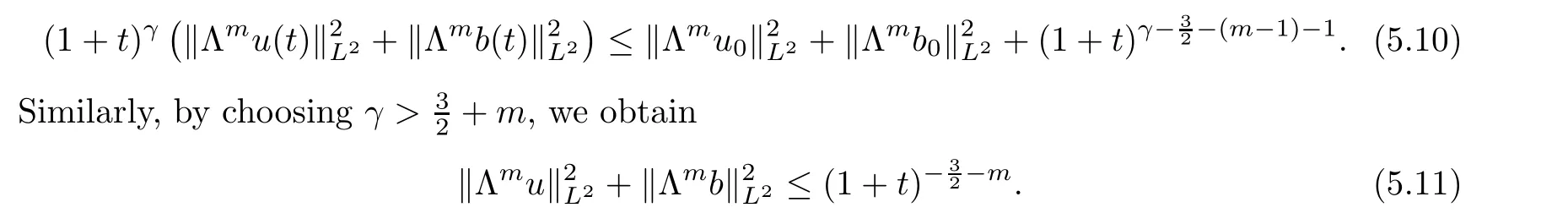

Therefore,the proof of Theorem 1.3 is completed.