联合仿真模型中代数环求解问题
王慧双 李琳琳

摘 要:FMI联合仿真标准,用来作为不同学科仿真工具的数据交互接口,将这些系统中由不同仿真工具建立的仿真过程以数据形式连接起来,形成统一的仿真耦合系统。反馈回路是许多复杂仿真系统在运用计算机技术进行系统仿真模拟时,由于计算机是按照一定的时序进行计算的,所以存在反馈回路的仿真系统就会产生代数环结构。该文通过引入解非线性方程组的方法解决FMI联合仿真系统中的代数环问题。
关键词:FMI联合仿真技术 代数环 tarjan算法 牛顿迭代法
中图分类号:O151 文献标识码:A文章编号:1672-3791(2021)05(a)-0038-03
Abstract: FMI joint simulation standard is used as the data interaction interface of simulation tools of different disciplines, which connects the simulation processes established by different simulation tools in these systems in the form of data to form a unified simulation coupling system. Feedback loop is a complex simulation system. When computer technology is used to simulate the system, because the computer calculates according to a certain time sequence, the simulation system with feedback loop will produce algebraic loop structure. In this paper, the algebraic loop problem in FMI joint simulation system is solved by introducing the method of solving nonlinear equations.
Key Words: FMI joint simulation technology; Algebraic rings; Tarjan algorithm; Newton's method
利用仿真模擬实际系统中的运行情况,进而实现系统的优化。考虑到各学科的耦合作用和影响,为了实现对研究对象在实际情况中更为精确、高效,多学科联合仿真的概念应运而生[1]。FMI联合仿真标准为多学科联合仿真模型提供了数据交互接口和通信协议。联合仿真系统中的代数环问题,影响着联合仿真的仿真精度与速度,该文应用DFS理论对各联合仿真模型之间的控制信息进行检索,并提出了一种基于解非线性方程的方法对联合仿真模型中的代数环结构进行求解。
1 基于tarjan算法的代数环检测
1.1 图论基础知识
1.1.1 强连通图
由有向边构成的图成为有向图,并且在有向图中的任意一顶点都有到达其他顶点的路径,则称为强连通图[2]。
1.1.2 强连通分量
在非强连通图中的连通部分。其中,独立的顶点也称为一个强连通分量。
1.2 Tarjan算法
Tarjan算法是基于对图深度优先搜索的算法,用于求解图的连通性问题,每个强连通分量为搜索树中的一颗子树,搜索时,把当前搜索树中未处理的顶点加入一个堆栈,回溯时可以判断栈顶到栈中的节点是否为一个强连通分量[3]。
该文利用Tarjan算法分析耦合系统形成的有向图,不仅可以检测出有向图中的强连通分量也就是耦合系统中的代数环,还可以计算出有向图中各个节点的赋值顺序,利用这个赋值顺序可以进行仿真初始化过程。
1.2.1 定义
DFN(u)为节点u搜索的次序编号(时间戳);LOW(u)为u或u的子树能够追溯到最早的栈中节点的次序号。
由定义可以得出,当DFN(u)= LOW(u)时,以u为根的搜索子树上所有节点为一个强连通分量[4]。
1.2.2 算法实现过程
(1)当检索到未被记录的点u时,DFN[u]=LOW[u]=time。
(2)每当搜索到一个点,把该点压入栈顶,当u和v有边相连时:
如果v不在栈中,DFS(v),并且LOW[u] = min{LOW(u),LOW(v)};
如果v在栈中,此时LOW[u] = min{LOW[u],DFN[v]}。
(3)当DFN[u]=LOW[u]时,将它以及在它之上的元素弹出栈,此时,弹出栈的结点构成一个强连通分量。
(4)继续搜索,直到图被遍历完毕。
2 基于牛顿法解代数环
牛顿法是将非线性方程线性化的过程[5]。其核心思想是利用泰勒级数展开(忽略二阶以上的项),通过不断迭代寻找导数为0的解,求得近似解。
首先针对一元函数利用牛顿法进行求解进行简单介绍。
2.1 一元函数推导过程
对于一元函数f(x)=0,将(x)在点x0处用泰勒公式进行展开(忽略二阶以上的项):
不断进行迭代,当梯度的模等于零或者函数值下降小于指定阈值,得到函数解X*。
牛頓法利用逐次逼近的方法,计算机运算速度快、适合做重复性操作,让计算机对一组指令进行重复执行,在每次执行这组指令时,都从变量的原值推出一个新值[6]。
牛顿法属于二阶收敛连,迭代速度相比简单迭代要快很多。但是,牛顿法对初值比较敏感,若初值不合适,系统很有可能会出现不收敛的情况,使得求解效率降低;另外,函数必须具有二阶偏导,计算量比较复杂。
3 实验结果对比
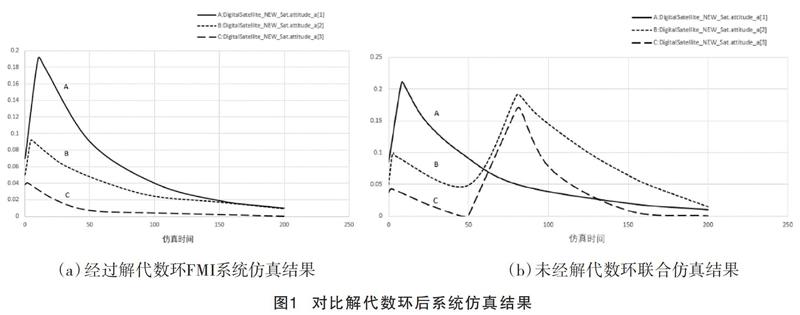
该次实验案例中采用的实验FMU模型有6个,分别为:卫星动力学模型、姿态轨道控制器模型、动量轮安装矩阵模型以及3个干扰模型。该实验中选择了动力学模型的3个输出端口参数attitude_a[1]、attitude_a[2]、attitude_a[3]作为参考数据,这3个参数分别代表了卫星在X轴、Y轴、Z轴3个方向的姿态角。
通过比较图1实验结果可以看出,解代数环的联合仿真模型仿真结果和未进行解代数环的联合模型仿真结果明显不同,经过求解代数环的系统仿真过程更稳定,仿真模型曲线更平滑,其所得结果也更精确。图1仿真结果对比验证了该文所述的代数环检测和求解算法的有效性。在未来面对多学科模型耦合的之间存在的代数环问题提出了效果较好的解决方案。
4 结语
随着联合仿真技术的快速发展,多学科之间的联合仿真验证过程,已经是开发系统性工程的必经之路。FMI联合仿真标准定义了多学科联合仿真的数据接口,打破了各学科仿真数据交互的壁垒。产品设计前的仿真可以有效降低产品开发成本和风险,同时可以促进各个学科领域的融合,提升科研成果转化为生产力的速度。
该文阐述代数环解析算法在该分布式FMI联合仿真系统中的应用实现过程,包括使用Tarjan算法进行代数环的检测、基于牛顿迭代法求解代数环的应用。通过卫星控制系统中相关仿真模型在系统中的仿真应用,验证了该文所论述的代数环检测和求解算法在分布式FMI仿真系统中的有效性和正确性。
参考文献
[1] 姚逸程.基于FMI标准的动力总成模型在环虚拟车辆仿真研究[D].浙江大学,2017.
[2] 徐泰华.社交网络中的子图结构挖掘研究[D].西南交通大学,2019.
[3] 胡全义.基于键合图的多领域统一建模与仿真技术研究[D].大连理工大学,2017.
[4] 杨维维.非线性方程组的算法及其在张量特征值的应用研究[D].南京航空航天大学,2017.
[5] 任露,黄颖为.基于牛顿迭代法的分形图像研究[J].西安理工大学学报,2016(2):247.
[6] 武海妮.改进的粒子群算法在求解非线性方程组中的应用[D].延安大学,2019.

