学生作锦，教师添花

梁笑韵 张代琴

【摘要】建构主义教学观认为，学习不是由教师把知识简单地传递给学生，而是学生在原有知识结构的基础上，经历动手操作、感官认知、建构新知识的过程。学习首先是学生自己的事情，学生通过积极地探索问题，由“被动接受”转为“主动建构”。新课程理念提倡让学生积极参与课堂，学生讲题是学生参与课堂的一种有效方式，可以较好地促进学生数学交流素养。

【关键词】建构主义教学观;圆周角定理;学生讲题

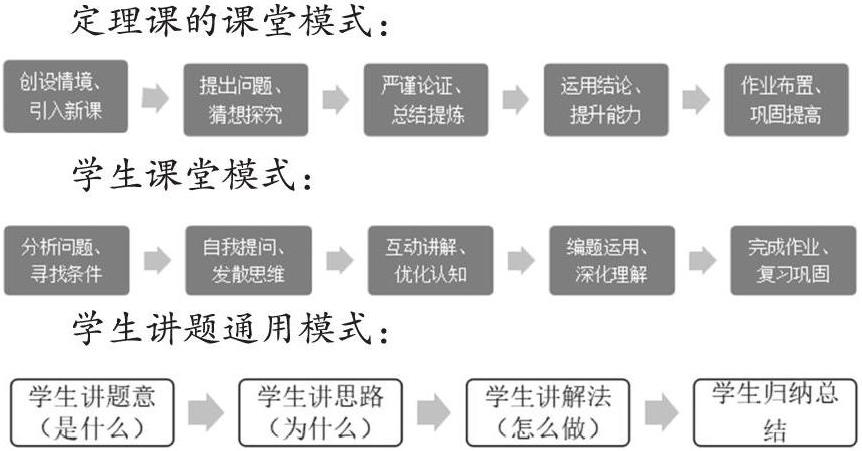
一、课堂师生换位，促进学生思维发展

数学教学是学生思维活动的教学，学生的思路应该由学生自己在头脑中产生，教师的作用是给学生创造条件，让他们尽可能发现更多的知识。很多老师觉得自己讲过的题目学生还会错，心理学研究表明：学生仅靠阅读来学习，只能记住10%;仅靠听教师讲解，只能记住26%;如果能把看到的、听到的和自己想到的用语言表达出来，90%能被记住。所以引导学生讲题，让学生展现自己的思维过程，是非常高效的学习方法。定理课的教学，是培养学生数学思维能力和提升学生数学认知水平发展的重要学习载体。以下通过一节定理学习课的片段，来介绍这种讲题教学模式。

二、学生讲题案例探索（圆周角定理证明）

1.教学内容分析：本节课是在学生学习了圆、弦、弧、圆心角、圆周角等相关概念的基础上出现的，圆周角和圆心角的关系通过弧为桥梁连接，这需要学生一定的几何观察能力。通过对圆周角定理的探讨，体验知识的形成过程，培养学生严谨的思维品质，为学生提供自主探索与交流展示的空间。

2.教学目标：理解圆周角定理，通过观察比较、发展学生的推理能力，在探索的过程中通过学生主动参与学会运用分类讨论、转化的数学思想解决问题。

3.教学手段：分组学习、合作探究。

4.教学过程简述。

【片段一】创设情境、引入新课

师：在上海的一次展览中，有一颗百万钻石被盗，而且钻石所在展位是监控盲区。在一个圆形展廳中安装监控器，每台监控角度是65°，为了监控整个展厅，最少需要在圆形边缘上安装多少台这样的监视器？

设计意图：数学来源于生活，又服务于生活，在教学设计中，利用数学问题的现实背景，选取一些有趣的例子引入课题，可以激发学生的兴趣。

师：解决这个问题，涉及到什么知识点？关键是求什么？

生：这个问题涉及到圆心角和圆周角的问题、关键是求角度。

【片段二】提出问题、猜想探究

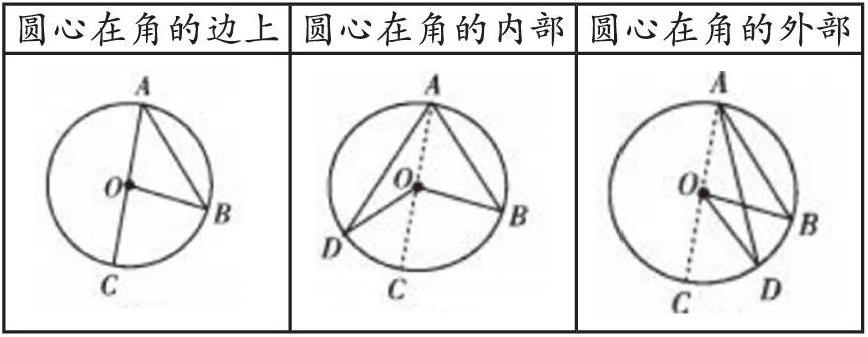
师：请学生在纸上画一个圆，并画出弧BC所对的圆心角和圆周角，进行分类。

生：投影小组画的图，发现弧BC所对的圆周角和圆心角的位置关系有三种：

圆心在角的边上 圆心在角的内部 圆心在角的外部

师：老师用几何画板动态演示，进一步让学生直观感受圆心与圆周角只有这三种位置关系。

设计意图：数学经常会用到分类讨论的方法，它是一种基本的数学思想，对于提高学生解题能力，发展思维的缜密性，具有重要作用。

师：请同学们猜想一下，弧BC所对的圆周角和圆心角的大小关系。

生：我们小组通过测量，发现弧BC所对的圆周角是圆心角的一半。我们组每个同学所画的圆以及所画的角的大小都不一样，但是我们都能得出相同的结论。

师：测量是个很便捷的方法，而且这位同学还考虑到圆的大小和角的大小等不同变量的情况，观察很仔细。

设计意图：学生动手操作画图，研究圆心角和圆周角的位置关系，教师把学生分组，引导学生通过观察小组成员画图，总结归纳以上三种情况。教师鼓励学生猜测圆周角和圆心角的大小关系，学生运用测量的手段得出这一结论，教师及时给予肯定，激发学生进一步探究知识的内驱力。

【片段三】严谨论证、总结提炼

师：数学定理的生成只靠猜想和度量是不够的，我们必须通过严谨的证明。现在请同学们尝试去证明你们的发现，即弧BC所对的圆周角是圆心角的一半。证明首先要转换已知和求证，你们会从那种情况开始证明呢？

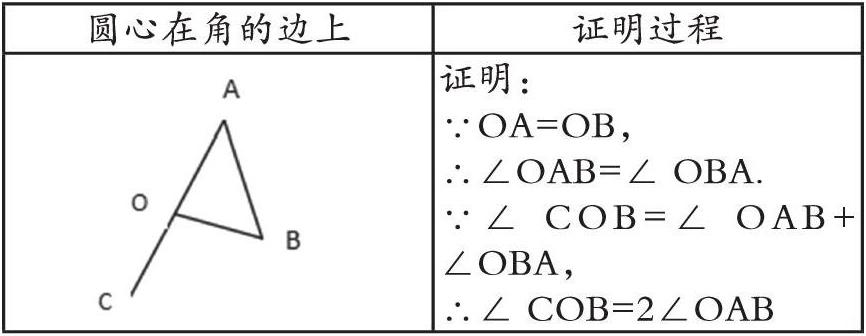
生：我先证明圆心在角的边上这种情况，我把要证明的图形简化如下：

圆心在角的边上 证明过程

证明：

∵OA=OB，

∴∠OAB=∠ OBA.

∵∠ COB=∠ OAB+ ∠OBA，

∴∠ COB=2∠OAB

师：非常好，你是怎么想到这个证明方法的呢？

生：我观察到圆心角∠COB是三角形的外角，圆周角∠OAB是三角形的内角，所以我就想到了用三角形的外角和定理来证明。

点评：我觉得比起证明过程，思考的过程更加重要，所以我会引导学生去讲述如何想到这个解题方法。这个解题方法受到题目哪些信息的影响，慢慢的学生就会从已知条件或者求证的结论入手，去寻找解决问题的方法。

师：那么圆心在圆周角的内部和圆心在圆周角外部时，我们怎样证明？

生：老师，我观察了第一种证明方法，我认为后面两个证明方法也是类似的，第一个模型就像一面小旗子，旗杆是圆的直径.而旗杆顶部的角等于旗杆中部角的一半，第二种情况就可以转化为求两个小旗子的两个旗杆顶部的角之和的形式，第三种情况是两面小红旗的顶部角之差的形式，我把我的证明过程展示一下。

师：非常棒，你特别地擅长观察、联想、类比，第二三种模型的证明，你巧妙地转化为已证的第一种模型，这就是运用了数学的化归思想和类比思想！太棒，

点评：学生通过学习圆周角定理的生成过程，进一步明白了几何定理证明的一般步骤，同时再次体会不同情况的分类证明，其证明方法可以借鉴已证的结论。通过自主探究 ，让学生学会运用分类讨论、化归的数学思想来研究问题 ，从而培养学生思维的严谨性。定理的学习需要学生更多的时间去探索，学生只有掌握了定理的来龙去脉，才能记得牢固，用的灵活。让学生经历证明方法的思考过程，熟悉其中的一些常见的转化关系，是对学生研究能力的培养，学生不断地积累经验，这样的数学学习才会让学生碰撞出更多的思维火花。