基于Canopy-K-means算法的半挂汽车列车行驶数据分析
李 兵, 屈亚洲, 熊 乐, 王晓亮, 赵晨光
(中汽研汽车检验中心(宁波)有限公司, 浙江 宁波 315336)
近年来,随着物流运输业的快速发展,半挂汽车列车在商用车市场的占比逐年增加。据统计[1],2013—2017年国内半挂牵引车年销量整体呈递增趋势,且2016和2017两年的年销量较上一年同比增长了55%和50%。而半挂汽车列车作为诱发重大交通安全事故的主要源头之一,其数量的增加势必会给其他交通参与者带来更多的潜在危险,因此,如何提高汽车列车行驶安全性一直是行业的研究热点。
Singh[2]利用相平面法提出了一定初始条件下半挂汽车列车系统相轨迹趋近和背离平衡点的变化规律,由此判定车辆的稳定和不稳定区域。关志伟等[3]采用线性系统稳态转向特性、非线性系统稳态转向特性和能量相平面3种方法对车辆转向稳定性进行了分析。李西涛[4]建立了半挂汽车列车非线性动力学模型,分析了其在极限工况下各状态变量平衡点的分岔现象,探讨了极限操纵工况下车辆的横向失稳机制。Ding等[5]利用分岔理论分析了恒定运行工况下半挂汽车列车非线性模型的稳定性,采用数值求解得到系统的稳定平衡点和不稳定平衡点,解释了常见的不稳定现象,并对状态空间中的稳定域进行了划分。陈林[6]基于卡尔曼滤波算法建立了以半挂牵引车的侧向加速度和横摆角速度为观测变量的状态估计器,并选择双移线和方向盘角阶跃工况试验对半挂汽车列车状态进行了估计分析。刘焕[7]建立了半挂汽车列车三自由度线性和非线性动力学模型,探究了车辆在不同行驶条件下的运动响应和失稳形式,并从能量变化角度对车辆的失稳机理进行解释,为判定车辆失稳提供了新的依据。彭涛等[8]基于Lyapunov法分析了车辆极限状态下的能量和能量变化阈值,求解得到半挂汽车列车高速变道稳定域,为车辆高速转向时的稳定性判定提供依据。综合以上文献可知,现有对半挂汽车列车稳定性分析大多是基于简化动力学模型进行的研究,存在所建模型不精确的问题。
为了解决这一问题,徐强[9]提出了一种基于K均值聚类分析的车辆横向稳定性判定方法,通过对车辆仿真数据进行聚类分析,划分了4种不同行驶状态,并设计仿真试验验证了该方法在双半挂汽车列车稳定性判定上的有效性,但是其聚类算法中的K值由经验确定,具有一定的主观性,影响对车辆行驶状态的准确划分,同时未进行实车试验验证该算法的有效性。翟德[10]利用K均值聚类算法对半挂汽车列车侧翻和折叠工况进行了研究,进一步验证了该方法在不同失稳形式下应用的有效性,但其缺点与文献[9]类似。基于以上考虑,本文首先采用Canopy算法对车辆行驶数据进行“粗”聚类分析,确定k值和初始状态聚类质心,然后在此基础上利用K-means算法对车辆行驶状态进行精确划分,并将仿真试验和实车试验结果相结合验证该方法的有效性。
1 系统建模
1.1 整车建模
由于本文主要从数据层面对半挂汽车列车行驶稳定性进行分析,需要大量的车辆行驶数据作为研究支撑,因此为了采集多工况下的行驶数据,选择TruckSim软件进行车辆动力学建模仿真,仿真所使用的车辆类型为3A Cab Over w/3A Euro Trailer。
1.2 仿真工况设计
依据《营运车辆抗侧翻稳定性试验方法 稳态圆周试验》(JT/T 884—2014)和《商用车辆电子稳定性控制系统性能要求及试验方法》(GB/T 8185—2019)试验工况要求进行仿真工况设计,见表1。

表1 仿真工况设计
表1中,定半径变车速选择速度为30~70 km/h,以5 km/h的间隔依次进行仿真工况设计,这里只以速度为变量,不考虑方向盘转角变化的影响;定车速变转角选择车速为40~60 km/h,方向盘转角为30°、60°、90°、120°,速度间隔为5 km/h依次进行仿真工况设计;J转向试验选择速度30~45 km/h,间隔为5 km/h,同样不考虑方向盘转角的影响。
2 车辆行驶数据分析
2.1 传统的K-means算法
K-means是一种简单的迭代型聚类算法,由于简单易修改、运行速度快,在数据挖掘领域应用非常广泛。其基本原理是:首先给定包含n个对象的样本集和聚簇个数k,然后从样本集中随机选择k个对象作为初始聚类质心,计算剩余样本集与初始聚类质心的欧氏距离,并将它们分配给与其欧氏距离最小的聚簇,再重新计算每个聚簇中各数据对象的均值作为新的聚类质心,不断重复这一过程直到各个聚簇的聚类质心不再变化或满足停止条件,从而实现同一聚簇中的对象相似度较高,而不同聚簇中的对象相似度较小,完成对样本集的划分。
由于K-means算法中的聚簇个数k必须预先给定,且初始聚类质心的选择是随机的,容易在迭代过程中形成大量冗余,使聚类结果陷入局部最优解[11]。因此,针对上述问题以及缩短聚类时间周期,采用Canopy-K-means聚类算法[12-13]对车辆行驶数据进行聚类划分。
2.2 基于Canopy优化的K-means算法
Canopy算法也是一种常见的聚类算法,是采用快速近似距离度量和两个距离阈值比较方式,实现快速粗聚类[14],由于其无须提前预设聚簇个数,因此可以在预处理阶段对车辆行驶数据进行“粗”聚类,确定聚簇个数k和初始聚类质心,然后再利用K-means算法进行“细”聚类,提高聚类结果的准确性。
Canopy-K-means算法流程如图1所示,可知在聚类工作开始之前,只需确定Canopy算法中的两个距离阈值T1、T2(T1>T2),K-means算法的迭代次数和目标函数的终止条件即可。
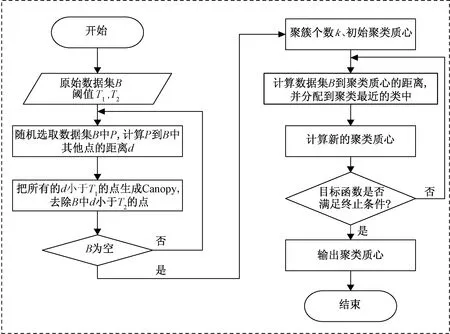
图1 Canopy-K-means算法流程
2.3 数据挖掘分析
根据1.2节设计的仿真工况进行仿真,得到各个工况下的车辆行驶数据。考虑到实车试验测试设备的可测变量,这里选取牵引车和挂车横摆角速度(w1、w2)、质心侧向加速度(ay1、ay2)和车身侧倾角(ψ1、ψ2)6个状态变量作为表征半挂汽车列车行驶稳定性的评价参数。结合各个工况的行驶特性,截取抗侧翻稳定性试验工况稳定时10 s的数据,截取J转向试验工况30 s的数据,采集共20 500组数据。为了便于对数据进行批量处理,将各个工况下采集的数据记为同一矩阵B=[w1i、w2i、ay1i、ay2i、ψ1i、ψ2i],其中,角标i代表矩阵B的行数,也即是某运行工况下某一时刻的车辆状态参数。
通过Canopy算法对矩阵B进行预处理,得到聚簇个数k=4,初始聚类质心

然后将Canopy的聚类结果代入K-means算法,得到的聚类结果如图2所示,每种聚类质心代表车辆的一种行驶状态。

图2 离线聚类结果
由图2可知,经过聚类之后,这些数据被自动化分为4个行驶状态,其中0~200 s为定车速变转角工况,0~40 s表示速度为40 km/h,方向盘转角为30°、60°、90°、120°时车辆的行驶状态变化,可以发现车辆在方向盘转角为30°和60°时为1状态,当转角增加到90°和120°时,车辆由1状态到2状态再变为3状态;40~200 s表示速度为45~60 km/h,在相同方向盘转角变化下,车辆行驶状态变化,其与 40 km/h 的状态变化类似,可知不同行驶状态的危险性高低依次为3、2、1。200~290 s是定半径变车速工况,随着车速的增加,车辆侧向加速度越来越大,稳定性降低,此时车辆的行驶状态也呈现1-2-3变化。290~410 s是J转向试验工况,表征30~45 km/h 下车辆的行驶状态,由于截取的是车辆刚进入弯道到驶出弯道的数据,车辆主要在3和4行驶状态变化,且当车辆在弯道行驶时,此时车辆处于4状态。综合以上分析可以得到:车辆不同行驶状态的危险性高低依次为4、3、2、1。
最后通过分析各聚类质心的特征值大小以及图2分析的行驶状态危险性高低,对聚类结果进行排序,结果见表2。

表2 基于Canopy-K-means算法得到的聚类质心
为了便于后续分析以及考虑到各特征值大小,这里参照文献[15]的方法对各行驶状态概括为3种危险等级状态。其中,行驶状态1和2统称为安全的行驶状态,行驶状态3为危险演化阶段,行驶状态4为潜在危险。
3 在线仿真平台搭建
3.1 工况设计
2.3节对车辆行驶数据进行了聚类分析,得到4种行驶状态类型,并根据各工况行驶特点,对各行驶状态下车辆的稳定性进行分析,获得各行驶状态的危险性高低依次为4>3>2>1。由于上述结论是基于不同工况下的行驶数据离线聚类得出的结果,因此这里选择抗侧翻稳定性和方向盘斜阶跃输入两种试验,来验证聚类结果的有效性,其中抗侧翻稳定性试验工况参数设置见表3,方向盘斜阶跃输入工况设计如图3所示。

表3 抗侧翻稳定性试验仿真工况设计
图3为方向盘转角随时间的变化曲线,其中0~2 s,方向盘转角为0°,车辆保持直线行驶,在2~10 s 方向盘转角匀速增加,在第10 s时达到180°,并保持180°不变,直至仿真结束。

图3 方向盘斜阶跃输入
3.2 在线识别
利用TruckSim和Simulink搭建了联合仿真平台,编写了计算欧氏距离的MATLAB Function函数,根据表3和图3所示工况依次进行仿真,其中表3所示工况只截取稳态行驶状态下10 s内的行驶数据进行分析,共500组数据,具体仿真处理结果如图4、图5所示。

图5 方向盘斜阶跃输入工况的欧氏距离在线识别
由图4可知,在0~10 s,车速为40 km/h时,处于第2行驶状态,此时车辆为安全状态;在10~20 s,车速为45 km/h时,车辆在第2和3行驶状态之间变化,表明车辆此时处于安全状态向危险演化状态的过渡阶段;在20~50 s,速度为50~60 km/h时,车辆一直维持在第3行驶状态,表明此时车辆处于危险演化状态。
由图5可知,在0~2 s直线行驶时,处于第1行驶状态,此时车辆为安全状态;在2~10 s方向盘转角匀速增加时,由第1、2行驶状态向3、4行驶状态变化,此时车辆逐渐由安全状态向危险演化状态和潜在危险状态过渡;在10~15 s保持方向盘转角为180°不变时,处于第4状态,此时车辆处于潜在危险状态。
综合以上两种试验工况的分析结果可知,在已知车辆行驶稳定性变化趋势的情况下,与根据离线聚类结果在线计算欧氏距离判定得到的行驶状态基本一致。因此,利用离线聚类结果对抗侧翻稳定性试验和方向盘斜阶跃输入工况的行驶稳定性判定是有效的。
4 实车验证
为了进一步验证聚类结果的准确性,这里以3.1节所列的试验工况进行实车试验,抗侧翻稳定性试验工况下行驶数据的选取方式与3.2节相同,同样只截取稳态行驶状态下10 s内的行驶数据,计算其与离线得到的聚类质心的欧氏距离。但考虑到实车试验的安全性以及内容研究的侧重点,半挂汽车列车选择在空载的试验条件下进行,试验样车如图6所示。

图6 试验样车
图7所示为根据车辆不同速度下的行驶数据与离线聚类质心计算得到的欧氏距离曲线,从各行驶状态的变化趋势来看,与图4所示的仿真结果基本一致,都是在0~10 s,车速为40 km/h时,处于第2行驶状态,10~20 s,车速为45 km/h时,车辆在第2和3行驶状态之间变化,20~50 s,速度为50~60 km/h 时,车辆一直维持在第3行驶状态,能明显表现出随着车速增加,车辆由安全向危险演化再向潜在危险状态的过渡过程。

图7 定半径变车速试验工况的欧氏距离
为了更清晰地表征车辆的行驶稳定性变化,绘制了不同速度下牵引车、半挂车侧向加速度及横摆角速度变化曲线,并采用12极无阶巴特沃斯滤波器对原始数据进行滤波处理,如图8所示。

图8 牵引车和半挂车侧向加速度、横摆角速度变化曲线
图8(a)和图8(b)为侧向加速度变化曲线,在0~10 s,也即为40 km/h时,牵引车和半挂车的侧向加速度大小约为0.1g;在10~40 s,随着速度的增加,两者的侧向加速度逐渐增大;当在40~50 s时,也即速度为60 km/h时,半挂车的侧向加速度大小相较于牵引车波动较大,且有明显的甩尾趋势,表明此时车辆的稳定性与之前相比较差。图8(c)和图8(d)为横摆角速度变化曲线,其整体变化趋势侧向加速度基本一致,都是随着速度的增加,数值逐渐增大,车辆的稳定性逐渐变差。
图9所示为在车辆速度为40 km/h、方向盘转角斜阶跃输入下的行驶数据与离线聚类质心计算得到的欧氏距离曲线,从各行驶状态的变化趋势来看,与图5所示的仿真结果基本一致。在0~20 s直线行驶时,处于第1行驶状态,此时车辆为安全状态;在20~35 s方向盘转角匀速增加时,由第1、2行驶状态向3、4行驶状态变化,此时车辆逐渐由安全状态向危险演化和潜在危险状态过渡;在35~40 s保持方向盘转角为180°不变时,处于第4行驶状态,此时车辆处于潜在危险状态。
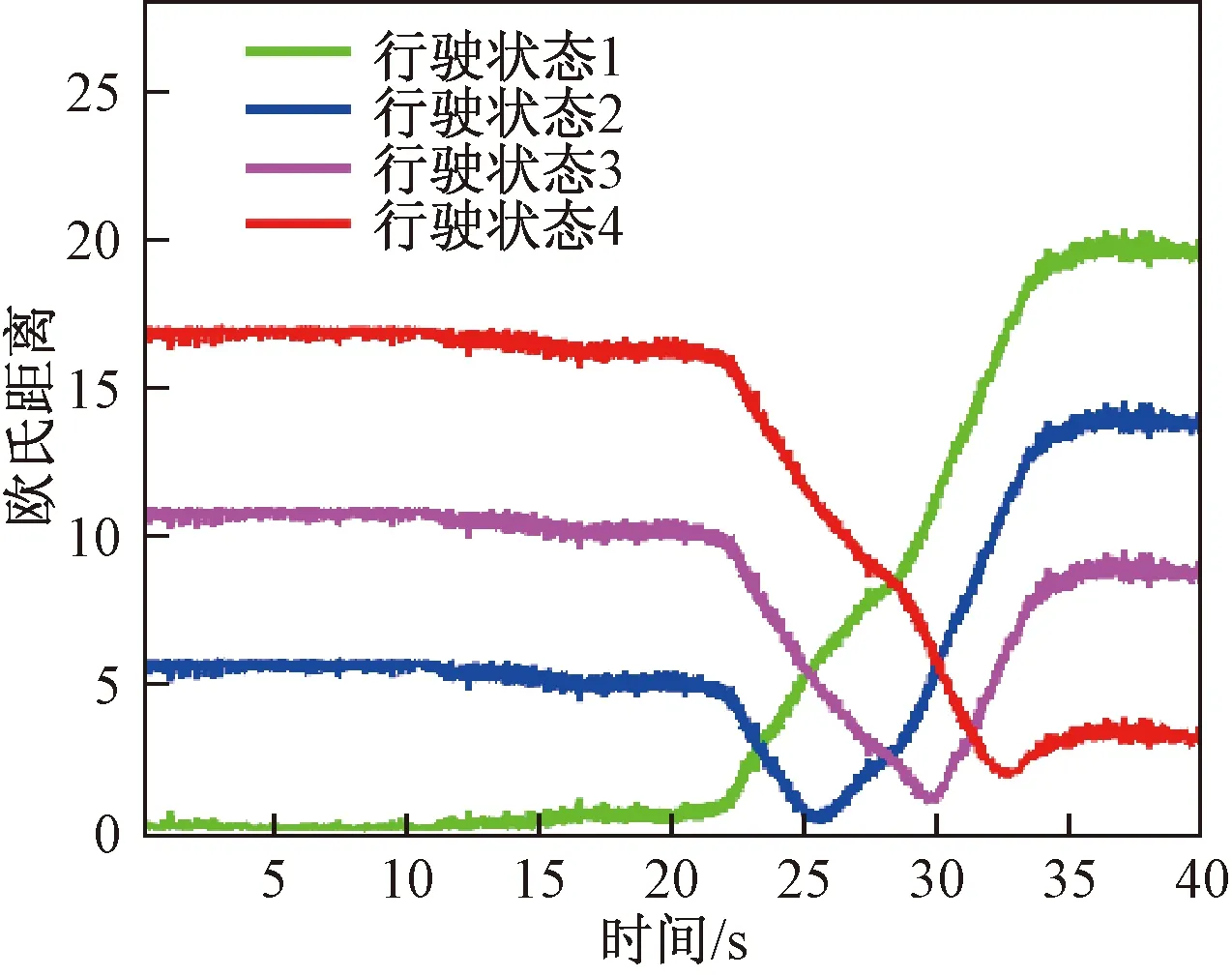
图9 方向盘斜阶跃输入工况的欧氏距离
为了更清晰地表征车辆的行驶稳定性变化,采用与定半径变车速试验工况的处理方法,绘制了牵引车、半挂车侧向加速度及横摆角速度变化曲线,如图10所示。

图10 牵引车和半挂车侧向加速度、横摆角速度变化曲线
图10(a)和图10(b)为侧向加速度变化曲线,在0~20 s,车辆以40 km/h的速度直线行驶,此时牵引车和半挂车的侧向加速度大小近似为0;在20~35 s,随着方向盘转角的匀速增加,两者的侧向加速度逐渐增大;当在35~40 s时,也即方向盘转角达到180°并保持不变时,半挂车的侧向加速度大小相较于牵引车波动较大,表明此时车辆的稳定性与之前相比较差。图10(c)和图10(d)为横摆角速度变化曲线,其整体变化趋势与侧向加速度基本一致,且都是随着方向盘转角的匀速增加,数值逐渐增大,车辆稳定性变差。
综合以上两种试验工况的分析结果可知,根据实车采集的行驶数据和离线聚类质心进行计算欧氏距离,判定得到的行驶状态与表征车辆行驶稳定性指标的变化基本一致。因此,从实车试验层面,验证了利用离线聚类结果对抗侧翻稳定性试验和方向盘斜阶跃输入工况的行驶稳定性判定也是有效的。
5 结语
选用TruckSim构建了半挂汽车列车整车模型,依据JT/T 884—2014和GB/T 38185—2019试验标准设计仿真工况并采集了车辆行驶数据,基于Canopy-K-means算法对行驶数据进行聚类分析,并搭建了在线联合仿真平台和实车试验验证平台,从仿真和实车试验两个层面验证该算法在车辆稳定性判定领域的可行性。结果表明,采用Canopy-K-means聚类算法可以对不同行驶状态数据进行分类,能够获得表征不同行驶安全特征的聚类质心,通过将定半径变车速、方向盘斜阶跃输入两种试验工况采集的行驶数据和聚类质心进行欧氏距离计算,判定得到的行驶状态与车辆所处工况下的行驶稳定性基本一致,能在一定程度上对车辆稳定性进行评价,因此可以使用表征不同行驶安全特征的聚类质心为车辆的控制和预警提供判定依据。

