初中生数学关键能力测评模型构建研究
朱立明
初中生数学关键能力测评模型构建研究
朱立明
(唐山师范学院 教育学院,河北 唐山 063000)
通过文献法、专家咨询法与层次分析法,在梳理数学关键能力内涵、要素与评价相关研究基础上,确定初中生数学关键能力三个测评维度,即数学观察能力(O)、数学思考能力(T)与数学表达能力(E),并对三个测评维度的权重值进行分配,得到初中生数学关键能力测评模型:A=0.23*O+0.40*T+0.37*E,经过专家认同度验证得到认可。
数学学科核心素养;数学关键能力;测评模型
一、研究问题的提出
2017年9月,中共中央办公厅、国务院办公厅印发的《关于深化教育体制机制改革的意见》指出:“在培养学生基础知识和基本技能的过程中,强化学生关键能力的培养,培养学生的认知能力、合作能力、创新能力、职业能力。”2018年1月,教育部印发的《普通高中数学课程标准(2017年版)》提出数学学科核心素养包含数学思维品质、数学关键能力以及情感、态度与价值观[1],这对于正在修订的义务教育数学课程标准具有重要的指引作用。数学教育开始从“知识本位”转向“素养本位”,其中数学关键能力占有核心地位,初中生数学关键能力也将成为义务教育数学课程的培养目标。因此,关于初中生数学关键能力操作性定义构建,构成要素的分析,以及测评维度的细化、测评模型的构建成为数学教育研究热点问题,本研究采用文献法、专家咨询法、层次分析法对初中生数学关键能力测评模型进行构建,为数学关键能力的落实与评价提供参考。
二、相关研究的综述
(一)数学关键能力内涵研究
数学关键能力内涵从其价值取向看大体可以划分为三类,即心理取向、技能取向与经验取向。基于心理取向的界定认为数学关键能力为完成数学活动或任务所具备的心理倾向[2],国内持有此类观点的学者大部分是基于苏联心理学家克鲁切茨基(Kruteskil)对中小学生数学能力的研究做出的阐述。基于技能取向的界定认为数学关键能力是学生完成数学问题解决所必需的技能与技巧,并在变化情境中精准地提出问题、分析问题、与解决问题[3]。基于经验取向的数学关键能力侧重数学基本活动经验,将数学关键能力定义为在不同的数学情境中,获得理解、判断与使用数学的经验[4]。这三种内涵各具特色,心理取向将数学关键能力视为能力的下位概念,强调其内隐性;技能取向将数学关键能力视为学生运用数学解决问题时所表现出来的技术,强调其外显性;经验取向将数学关键能力视为学生学习经验,强调其生成性[5]。
(二)数学关键能力要素研究
数学关键能力要素是剖析其内部构成的关键,目前研究更多集中在对其成分的探讨。从国家层面来看,在各国数学课程标准中,均提出数学关键能力的构成要素。例如,我国数学课程标准提出计算能力,逻辑推理能力与空间想象能力[6],德国基于PISA数学素养测评框架,提出构建数学论证、数学地解决问题、数学建模、数学表征的应用、数学符号公式以及技巧的熟练掌握和数学交流六大数学能力[7]。2010年,《美国共同核心州数学标准》(CCSSM)中涉及八大数学能力,即理解并解决问题、推理、论证并评价他人推理、数学建模、使用合适的工具、精确化、探求并利用数学结构以及探求规律[8]。澳大利亚并非直接提出数学能力,而是结合数学、科学、英语等学科共同提出七大能力,再从数学学科视角对七大能力进行阐述[9]。从个人层面来看,各国学者也在探讨数学能力的构成,例如,克鲁切茨基的数学能力构成对学者们的影响较大,尼斯提出“数学能力之花”模型,具体包含数学思维、提出并解决数学问题、数学建模、数学推理、数学表征、数学符号化与形式化、数学交流、工具的使用等数学能力[10],喻平将数学能力分为三大类,包含自我监控能力、数学阅读能力等11种数学能力[11]等。还有从数学学科核心素养视角将数学关键能力划分为数学抽象与表达能力、数学运算能力、数学猜想与论证能力、数学想象与化归能力、数据分析与预测能力、问题解决与交流能力[12]。无论是各国数学课程标准,还是学者们的相关研究,观其构成要素,均含有数学推理、数学交流、问题解决等关键词,缺少对测评指标的进一步构建与描述。
(三)数学关键能力评价研究
国际学生评估项目(Program for International Student Assessment,简称PISA)倾向于数学素养评价,构建了内容、过程与情境三维一体的测评目标结构,包含了知识、能力、情境三个测评维度,着重考查15岁中学生对于未来生活可能面临的问题情境、准备的程度及习得的必备的知识与技能[13]。PISA2021数学素养测评框架开始注重个人在不同真实世界情境下进行数学推理与表达运用数学解决问题的能力,具体包括使用数学概念、过程、事实和工具来描述、解释和预测现象的能力[14]。曹一鸣等从学习理解、实践应用、创造迁移三个维度、九个子维度构建了学生数学学科能力测试框架[15]。杜宵丰等基于对八万名学生的几何典型错例分析,从了解、理解、掌握、运用四个层次,对八年级学生数学能力进行测评[16]。张晋宇等对数学表征与变换能力测评指标进行综述,得出再现水平、联系水平、反思水平三个测量水平,并对其具体行为进行描述[17]。
(四)数学关键能力已有研究述评
通过相关研究文献梳理可以看出,国内数学关键能力研究以理论研究为主,而实证研究比较缺乏。随着数学学科核心素养的不断推进与落实,学者对数学关键能力的研究也逐渐从理论走向实践。纵观目前已有研究,在以下四个方面仍需改进:第一,数学关键能力操作性定义仍需完善,应从“理论层面”转向与“操作层面”的结合;第二,数学关键能力的研究方法需要多元化,需要理论思辨与实证研究相结合;第三,数学关键能力测评研究比较匮乏,需继续构建并完善测评模型,模型的科学性与可行性也有待检验;第四,目前数学关键能力研究对象更多关注小学生与高中生,较少针对初中生数学关键能力研究。鉴于此,本研究以初中生为对象,构建数学关键能力的测评模型。
三、研究的设计与方法
(一)研究样本的选取
初中生数学关键能力测评维度及其权重的确定,主要借助专家咨询,因此需要确定专家样本。本研究的专家群体由高校数学教育专家、初中数学教研员与初中数学骨干教师组成,其中高校数学教育专家在数学素养、数学核心素养、数学能力等领域都有研究。这样的专家组合可以为数学关键能力测评模型构建提供理论支撑与实践参考,通过专家建议对测评维度进行修改与调整,实现测评维度的科学性与合理性。
在选择学生样本的时候,首先确定学校,将样本学校分成3类,一类是优质学校,二类是中等学校,三类是薄弱学校,同时这些学校满足以下两个条件:一是能够代表同等城市的经济、教育发展水平;二是便于开展研究,能够保证调查的可行性与所得数据的真实性。基于以上两方面,结合学缘、师缘、友缘等因素,选取唐山、天津、长春、东莞、海口等城市,每个样本城市各选取一类学校,在每所学校均选择初二年级学生作为样本,这是因为初一年级学生刚刚步入初中,而初三年级学生具有中考压力。共发放试卷1 127份,回收有效问卷1 066份,有效率为94.5%,其中优质学校学生样本量324,中等学校学生样本量为375,薄弱学校学生样本量为367,样本结构大体均衡。
(二)研究方法的运用
本研究采用文献法、专家咨询法、统计分析法与层次分析法等研究方法。首先借助文献法,对数学关键能力的内涵、要素与评价的相关研究进行梳理,从中获得数学关键能力的高频词。其次,以此为基础初步形成初中数学关键能力的维度,并编制专家问卷进行专家咨询,运用探索性因素分析与验证性因素分析形成数学关键能力测评维度。最后,借助层次分析法对初中生数学抽象能力各维度的权重进行赋值,并进行专家认同度检验,形成初中生数学关键能力的测评模型。
(三)研究思路的分析
从测评指标构建的逻辑顺序来看,指标体系构建有三种范式:自上而下的范式、自下而上的范式、上下混合的范式[18]。本研究借鉴教材难易度模型[19]、学生课业负担测评模型[20]、数学符号意识测评模型[21]、学校特色发展测评模型[22]、初中生信息技术素养测评模型[23]等人文社科领域多种测评模型构建的基本思路,在构建测评指标时综合考量“自上而下”和“自下而上”两构建范式的优点,在开展理论研究与文献梳理的同时,广泛征求相关领域专家和有关人士的意见和建议,兼顾理论与实践的双重取向形成测评维度体系。在研究中,充分挖掘初中生数学关键能力测评模型构建的理论依据,使测评维度体系构建研究过程更具有针对性,研究思路更加清晰,相关研究领域的专家和有关人士所提意见与建议更加具体,同时征求专家的意见,使整个研究过程具有开放性、民主性与实践性。
四、初中生数学关键能力测评模型构建
(一)测评维度的遴选
由于学段的不同,初中生数学关键能力与高中生、小学生的表现各不相同,通过文献综述可以看出,数学关键能力的高频词包含数学推理、数学交流、问题解决等方面。《义务教育数学课程标准(2011年版)》(以下简称《课程标准(2011年版)》)指出:“数学课程能使学生掌握必备的基础和基本技能基础上,培养学生的抽象思维和推理能力,培养学生的创新意识和实践能力。”[24]而在目标的划分上,也提到了数学思考与问题解决。此外史宁中教授指出数学教育在于培养学生会用数学的眼光观察世界,会用数学思维思考世界,会用数学语言表达世界[25]。因此,通过相关文献梳理,结合初中生认知水平特征与初中数学课程内容,初步将初中生数学关键能力测评维度确定为:问题解决、数学交流、符号运用、数学观察、数学思考、数学表达。
(二)专家咨询结果分析
以问题解决、数学交流、符号运用、数学观察、数学思考、数学表达6个核心词为基础,编制Likert五级量,从“非常不同意”到“非常同意”,依次赋分为1-5,并添加是否有删减与增补题项,进行第一次专家咨询,征求了来自北京、长春、重庆、天津、杭州、海口等6个城市的31位数学教育专家的意见,其中,高校数学教育专家7位,有2位专家是《课程标准(2011年版)》修订组成员,数学教研员8位,初中数学教师14位。
专家咨询结果如表1所示,从集中程度来看,各类专家对初中生数学关键能力各测评维度的平均分分布在2.525-4.331,其中,数学交流(3.525)、符号运用(3.651)两个维度专家平均分低于3.75(3.75是5分量表的75%等级值),其余维度均高于4;从离散程度看,初中生数学关键能力各测评维度的标准差在0.499-0.682之间,所有测评维度的标准差较小,说明专家意见波动不大,相对比较集中。初中生数学关键能力各测评维度的变异系数在0.132-0.170之间(数值均较小),反映了所选取的专家群体对于各测评维度协调程度较高。
通过个别专家访谈,其中一位《课程标准(2017年版)》修订专家认为:“数学关键能力还是一个相对比较泛化的概念,具体可以细化为抽象能力、推理能力、运算能力等数学能力,有一点,数学关键能力离不开数学知识,在观察、思考与问题解决过程中,在一定程度上就包括了‘数学交流’,同时符号运用可以在问题解决中得以体现,也可以在数学表达中体现。”还有专家指出:“问题解决可以细化到其他维度,例如在数学观察中其实不是为了观察而观察,也是在解决问题,比如形成数学概念,又或者在数学表达过程中,也是在解决问题。”
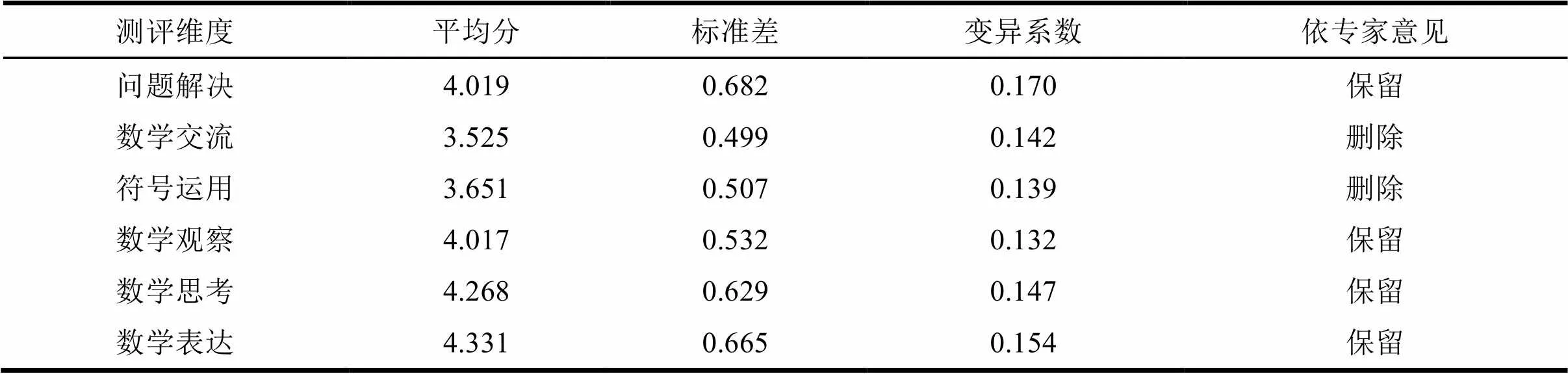
表1 初中生数学关键能力测评维度第一次专家咨询意见统计
通过第一次专家咨询,综合考虑专家建议以及集中度、离散度、变异系数三个统计量,将初中生数学关键能力测评维度调整为问题解决、数学观察、数学思考、数学表达。
(三)探索性因素分析
以问题解决、数学观察、数学思考、数学表达4个维度为基础,组织数学教育专家、初中数学教研员与初中数学骨干教师编制测评题项,经过反复商讨与修改,形成正式测试题,共16个题项(T1、T2、T3、……、T16),如表2所示,对533名初二学生的试卷进行探索性因素分析。

表2 测评维度维度及其对应的测评题项

表3 初中生数学关键能力测评维度旋转成分矩阵
以16个测评题项得分进行探索性因素分析,KMO值为0.923,Bartlett球形检验χ2值为457.977(df=66,p=0.00)达到极显著水平,说明适合做因素分析,主成分分析采取提取特征值大于1的共同因素如表3所示,结合原测试题项,可以得到以下结果:第一,通过主成分分析,可以得到3个因素,由原来4个测评维度,降为3个;第二,特征概括维度题项被重新划分,T3、T5与T4、T6、T7、T8构成一个因素,T2与T9、T10、T11、T14构成一个因素,T1与T12、T13、T15、T16为一个因素。三个因素特征值分别为4.151,2.412,1.889,三个因素构念联合解释变异量为66.576%,大于60%,第一个因素最大因素负荷量为0.854,第二个因素最大因素负荷量为0.886,第三个因素最大因素负荷量为0.805,因素负荷量情况较好,旋转后的因素负荷矩阵和累积解释变异量表明提取的三个因素对整个测评问卷的有效程度较好,最后将初中生数学关键能力三个测评维度分别命名为:数学观察能力(Observation-O)、数学思考能力(Thinking-T)、数学表达能力(Express- ion-E)。
(四)验证性因素分析
利用AMOS21.0作为CFA计算工具,利用其余533名初二学生测试卷结果进行验证因素分析,如表4所示,从表4可以看出,P值为0.000<0.05,卡方自由度的比值为1.873<3.000,RMR值等于0.032<0.05,指标GFI的值为0.946,IFI的值为0.977,CFI的值为0.955,三个值均大于0.900,RMSEA值等于0.042<0.05,说明模型适配较好[26]。综合各项指标参数,一阶3因子模型拟合程度较好。由相关性分析结果显示,一阶因子概念之间存在高度相关性,初中生数学关键能力测评维度模型的基本适配指标均达到检验标准。

表4 一阶3因子模型拟合指数
(五)权重系数的确定
为确定初中生数学关键能力各维度的权重值,重新对31位数学教育专家进行第二次专家咨询,回收有效问卷27份,有效率为87.1%,下面利用层次分析法,对初中生数学关键能力测评维度的权重值进行计算。选择其中一位专家对数学关键能力维度的评分为例,其判断矩阵如表5所示。

表5 某专家对初中生数学关键能力测评维度判断矩阵
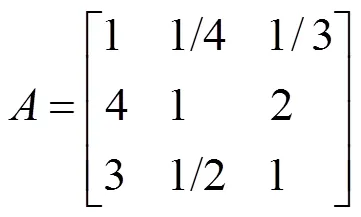
将初中生数学关键能力各维度判断矩阵的每列原元素作归一化处理,其元素的一般项为:
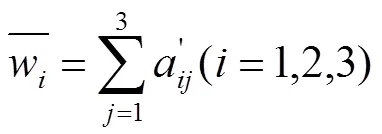
计算出判断矩阵的特征向量
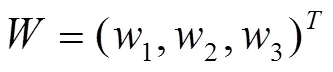
其中
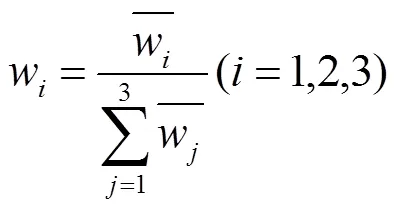
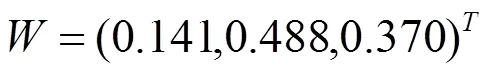
因此,该专家认为初中生数学关键能力的三个维度,即数学观察能力、数学思考能力、数学表达能力的权重依次为0.14,0.49与0.37。
为了达到对维度相对重要程度的判断相容,即一致性的要求,需要对计算出的初中生数学关键能力维度的权重进行检验,其标准如下:
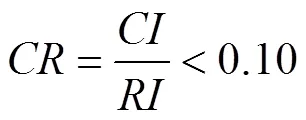
时,其中

便认为达到了相容程度,超过这个比值,则需要对维度的权重加以重新修整。以该专家评分进行计算,

当为3时,随机一致性变量值为0.58,
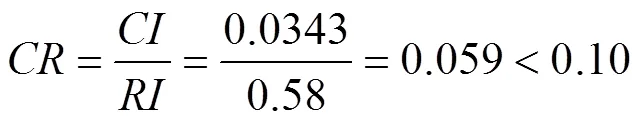
因此,认为该专家在初中数学关键能力三个维度权重的判断上达到相容程度,满足一致性要求[27]。
依次对剩余26位专家评分构建判断矩阵、计算特征向量和相容程度检验,其中有7位专家的评分数据未通过检验,因此,实际有效的专家评分共20个,通过计算20位专家在初中生数学关键能力各测评维度权重的平均值,为方便计算与操作,将权重值保留小数点后两位有效数字。数学观察能力、数学思考能力与数学表达能力三个测评维度最终权重值依次为0.23,0.37,0.40。初中生数学关键能力表达式为
=0.23*+0.40*+0.37*。
(六)专家认同度分析
以初中生数学关键能力测评维度与测评模型为内容编制专家问卷,进行第三次专家咨询,请专家根据自己的理解在“非常认同”“比较认同”“不确定”“比较不认同”“非常不认同”五个选项中做出选择。专家结构包含了高校数学教育专家、初中数学教研员与初中数学骨干教师,共回收问卷215份,有效问卷197份,有效率为91.6%,其中高校数学教育领域专家31人,初中数学教研员44人,初中数学骨干教师122人。调查结果如表6所示,专家群体对初中生数学关键能力测评维度与测评模型认同度较高,在“非常认同”与“比较认同”上,数学思考能力认同度为92.67%,数学思考能力认同度为93.84%,数学表达能力认同度为97.17%,测评模型的认同度为94.29%,借助方差分析,三种不同类型的专家在测评维度与测评模型的认同度上没有显著性差异,反映了专家群体认同度协调程度较高。
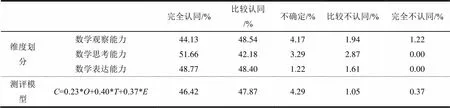
表6 专家群体对初中生数学关键能力测评模型认同度
五、结论与展望
本研究基于初中生认知水平与数学课程,构建了初中生数学关键能力测评模型,其表达式为
=0.23*+0.40*+0.37*,
通过专家认同度调查,初中生数学关键能力测评模型具有较好的有效性和可靠性,能够作为测量初中生数学关键能力的基本框架,有利于实现其测评的科学性与操作性。诚然,研究受到时间与区域的限制,所构建的模型仍需进一步完善,在后续研究中,将对每个维度的操作指标进行厘定,进而形成测评工具,诊断初中生数学抽象、推理与建模能力实然发展水平[28]。
[1] 中华人民共和国教育部.普通高中数学课程标准(2017年版)[S].北京:人民教育出版社,2018:4.
[2] 鲍建生.关于数学能力的几点思考[J].人民教育,2014(5): 48-51.
[3] F E Weinert. Leistungsmessung in Schulen[M]. Weinheim and Basel: Beltz, 2003: 17-23.
[4] 朱立明.高中数学教学类型的理论探析:数学学科核心素养视角[J].唐山师范学院学报,2020,42(3):148-152.
[5] 朱立明.高中生数学关键能力研究的追溯与前瞻[J].天津师范大学学报(基础教育版),2019,20(4):32-35.
[6] 课程教材研究所.教学大纲汇编(数学卷)[G]//20世纪中国中小学课程标准.北京:北京师范大学出版社,1999:434.
[7] 徐斌艳.旨在诊断与改进教学的数学学科能力测评分析——来自德国的实践[J].全球教育展望,2011,40(12):78- 83.
[8] Common Core State Standards Initiative. Common Core State Standards for Mahtematics[EB/OL].(2013-01-01) [2021-06-23].http://www.corestandards.org/assets/CCSSI_Math%20Standards.pdf.
[9] The Australian Curriculum. Assessment and Reporting Authority(ACARA). The Australian Curriculum General Capabilities[EB/OL].(2013-01-01)[2021-06-23].http://www.australiancurriculum.edu.au/Mathematics/General-capabilities.
[10] Mogens Niss. Mathematical Competencies and the Learning of Mathematics: The Danish KOM Project [EB/OL].(2013-01-01)[2021-06-23].http://w3.msi.vxu.se/users/hso/aaa_niss.pdf.
[11] 喻平.数学教学心理学[M].北京:北京师范大学出版社, 2010:296-303.
[12] 朱立明.高中生数学关键能力测评指标体系的构建[J].课程·教材·教法,2020,40(3):34-42.
[13] Programme for International Student Assessment. The PISA2003 Assessment Framework: Mathematics, Read- ing, Science and Problem Solving Knowledge and Skills [EB/OL].(2013-01-01)[2021-06-23].http://www.pisa.oecd. org/document/29/0,3746,ed_32252351_32236172_33694301_1_1_1_1,00.html.
[14] 董连春,吴立宝,王立东.PISA2021数学素养测评框架评介[J].数学教育学报,2019,28(4):6-11.
[15] 曹一鸣,刘晓婷,郭衎.数学学科能力及其表现研究[J].教育学报,2016,12(4):73-78.
[16] 杜宵丰,吝孟蔚,黄迪.八年级学生数学能力测评及教学建议——基于八万名学生几何典型错例分析[J].教育测量与评价,2014,7(12):35-39,54.
[17] 张晋宇,姜慧慧,谢海燕.数学表征与变换能力的评价指标体系研究综述[J].全球教育展望,2016,45(11):13-21.
[18] 范涌峰,宋乃庆.大数据时代的教育测评模型及其范式构建[J].中国社会科学,2019,40(12):139-155.
[19] 蔡庆有,邝孔秀,宋乃庆.小学数学教材难度模型研究[J].教育学报,2013,9(5):97-105.
[20] 宋乃庆,杨欣,王定华,朱德全.学生课业负担测评模型的构建研究——以义务教育阶段学生为例[J].西南大学学报(社会科学版),2015,41(3):75-81.
[21] 李艳琴,宋乃庆.小学低学段数学符号意识测评指标体系的初步构建[J].教育学报,2016,12(4):23-28.
[22] 范涌峰,宋乃庆.学校特色发展测评模型构建研究[J].华东师范大学学报(教育科学版),2018,36(2):68-78.
[23] 张辉蓉,等.初中生信息技术素养测评模型构建研究[J].中国电化教育,2017,38(9):33-38.
[24] 中华人民共和国教育部.义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2012:1.
[25] 史宁中.学科核心素养的培养与教学——以数学学科核心素养的培养为例[J].中小学管理, 2017, 35(1): 35-37.
[26] 吴明隆.结构方程模型:AMOS的操作与应用[M].重庆:重庆大学出版社,2009:236-237.
[27] 吴钢.现代教育评价基础(修订版)[M].上海:学林出版社, 2006:139-142.
[28] 唐丽艳.高中生数学建模能力发展状况调查研究——以核心素养为视角[J].唐山师范学院学报,2020,42(6):148- 153.
Research on Evaluation Model Construction of Middle School Students' Key Ability in Mathematics
ZHU Li-ming
(School of Education, Tangshan Normal University, Tangshan 063000, China)
With the proposal and development of the key competence in mathematics, the key ability of junior middle school students in mathematics has become an important ability goal of mathematics curriculum in compulsory education stage, and it is also a hot topic of mathematics education research. Three measurement dimensions of key mathematical abilities of junior middle school students are determined, namely, mathematical observation ability (O), mathematical thinking ability (T) and mathematical expression ability (E), through literature method, expert consultation method and analytic hierarchy process, on the basis of combing the connotation, elements and evaluation of key mathematical abilities, and the weight values of the three measurement dimensions were distributed, the evaluation model of junior middle school students’ mathematical key ability was obtained: A=0.23*O+0.40*T+0.37*E, which was approved by experts’ recognition.
the key competence in mathematics; the key ability in mathematics; the evaluation model
G625.5
A
1009-9115(2021)04-0139-07
10.3969/j.issn.1009-9115.2021.04.027
河北省教育厅青年拔尖人才项目(BJ2020213),唐山师范学院教育教学改革研究项目(2018001003)
2021-02-21
2021-06-24
朱立明(1986-),男,满族,河北承德人,博士,副教授,研究方向为课程与教学论、数学教育。
(责任编辑、校对:高俊霞)

