水库大坝工程深基坑支护安全性的有限元分析

杨 莹

(新疆水利水电勘测设计研究院，乌鲁木齐 830000)

0 引 言

基坑工程作为建筑项目中的基础子工程，在基坑开挖时，需要对周边土体进行支护，以保证工程的顺利开展[1-3]。但对于支护要求较高，同时由于在开挖过程中，施加在支护架上的应力会出现变化，因此对于支护架的位移预测计算较为困难[4-5]。在早期基坑支护安全性的研究中，通常只能使用现有公式对于当前土体、支护材料以及开挖深度等指标进行带入，大致得出需要的应力。在进行支护时，则往往发现支护架的位移误差远大于实际理论误差值。随着计算机技术的应用，利用计算机的计算能力可以对影响基坑支护安全的参数进行导入，并进行大量计算，得出相对准确的数据。但结果仍是由固定公式给出，结果准确性仍难以满足需求[6-8]。现在已开发出有限元分析法，该方法可以实现动态应力分析，大大提高了基坑支护安全性分析结果的准确度。但当前的分析结果缺乏对支护状态和基坑土体中互斥性的考虑，仍有改善空间[9-11]。

1 水库大坝工程深基坑支护安全性的有限元分析方法设计

1.1 基坑支护安全性物元描述

传统有限元分析中，难以将支护状态下的互斥问题相容化，影响分析结果的可靠性[12-13]。因此，本文选择采用物元分析法对支护的安全性首先进行物元描述，保证其中存在互斥问题可以共同分析。首先设描述对象为N，支护下的性状为C，状态下的量值V，描述中的主要元素为R=(N，C，V)并作为主要元素，并构成物元。而当基坑支护N中，存在若干性状，则得出n个特征c1、c2、…、cn以及相对应的量值v1、v2、…、vn描述，表示为：

(1)

而通常情况下，支护与基坑之间可以看作存在客观性矛盾的两个个体，采用N0代表该支护结构的参照标准，并将性状ci的值限定为ari≤vn≤bri，而其中的经典域物元矩阵则可以表示为：

(2)

同时需要对上述公式中的数据进行关联函数计算。假设元素集中的元素定义范围为X0=[a,b]，那么元素模量则为|X0|=|b-a|，而在定义集合中的任一点X距离定义范围X0=[a,b]的距离如下计算：

(3)

同时其中的关联函数则可以表示如下：

(4)

式中：p(X,X0)为在点X与范围X0=[a,b]的差距；p(X,Xp)为点X与范围Xp=[ap,bp]的差距；X为支护结构的物元量值；X0为经典域物元下的取值幅度；Xp为节域物元的取值幅度。

通过计算以上数值，确定基坑和支护之间的物元描述和误差值，运用该数值在有限元分析结果的数值中进行误差修正。

1.2 支护状态有限元模拟

在分析基坑支护的安全性之前，需要将基坑土体的应力进行模拟分析[14-15]。在基坑处于静止不动状态时，围护机构不存在左右位移，土体本身处在弹性平衡状态。对于支护中，静止土体的压力则为：

P0=(∑γihi+q)K0

(5)

式中：γi为支护点位上的土层重度，kN/m3；q为支护边坡地面的均布荷载，kPa；hi为支护点位上的土层厚度，m；K0为支护点位上土体的静止土压力系数；P0为支护点位上土体的静止压力强度，kPa。

同时根据上述内容中对于基坑和支护之间的物元描述，将参数和计算方法引入有限元分析软件中，利用有限元分析软件可以模拟支护在开挖状态下的力学变化。当基坑开挖时，由于土体的自重应力发生改变，土体中的应力分布将会随着变化，对于支护的安全性也会出现改变。在有限元模拟下，将基坑开挖状态下的网格图形态进行呈现，见图1。

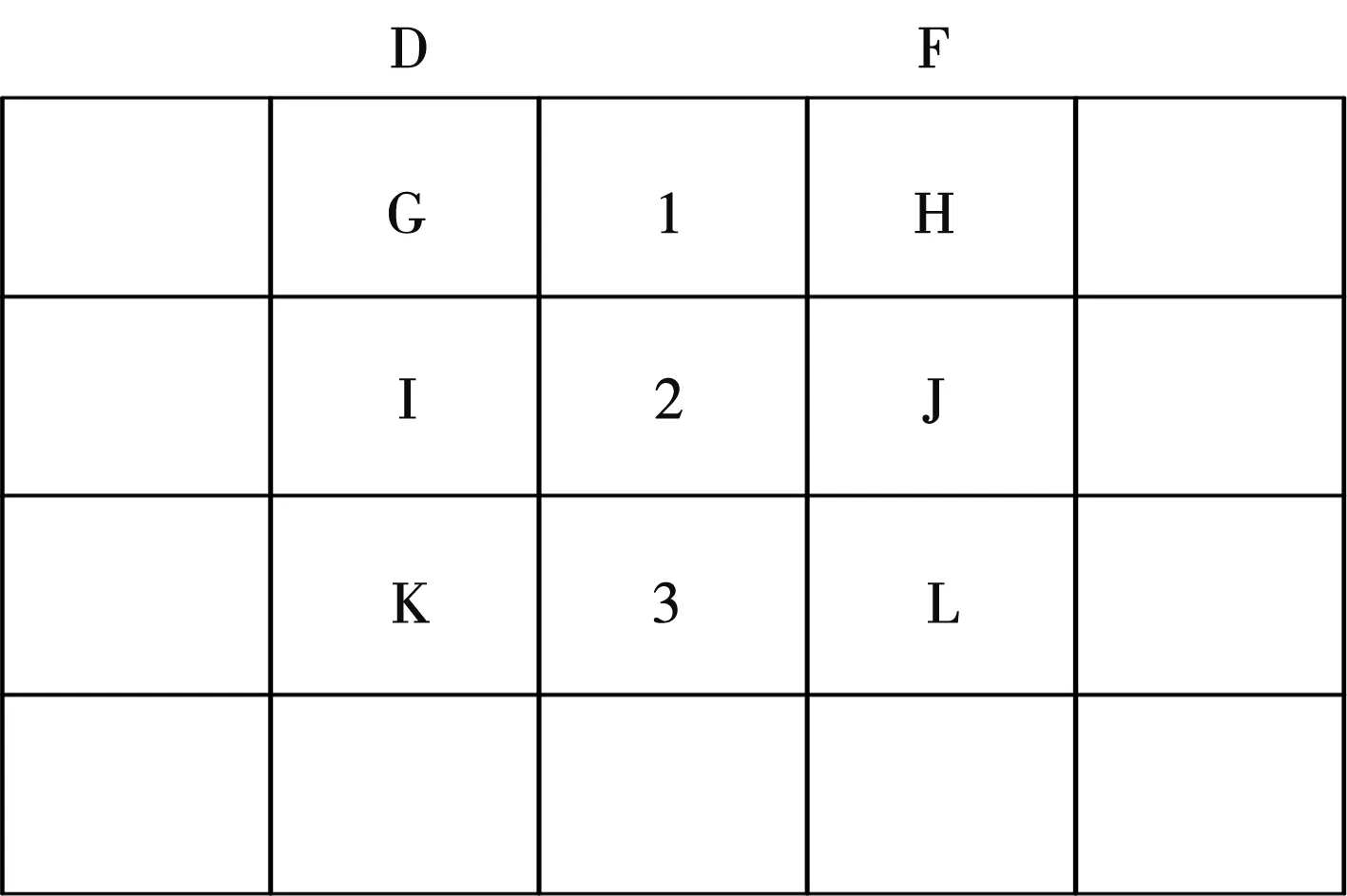
图1 有限元开挖模拟示意图

在图1中，将土体分为多级，实际级数根据工程实际规划拟定。其中，一级为DFGH，二级为GHIJ，三级则为IJKL。在开挖过程中，开挖土体对于其下部土体作用的等效节点力由自重力得出，即{f}1、{f}2、{f}3。同时根据该地层的地基应力状态，包括天然应力状态{σ0}、开挖应变状态{ε0}以及土体位移状态{δ0}，可以得到对应的内力变形：

(6)

根据上述公式，得出对应开挖面的节点力，获得有限元的动态力矩模型，以此作为安全性分析的基础参数值。

1.3 有限元折减安全系数计算

本文在进行有限元折减安全系数中，采用强度参数标准值来进行开挖和计算，参数可由上述计算和有限元分析软件得出，并得到基坑开挖到坑底的应力状态并进行迭代计算，以得到安全系数。其中，在进行迭代计算位移增量的公式为：

(7)

式中：δdi为经过第i次迭代的位移子增量；{σi-1}为经过第i次迭代开始的应力稳定值；{F}为支护承载的外部荷载。

在计算过程中，应力点的位置见图2。

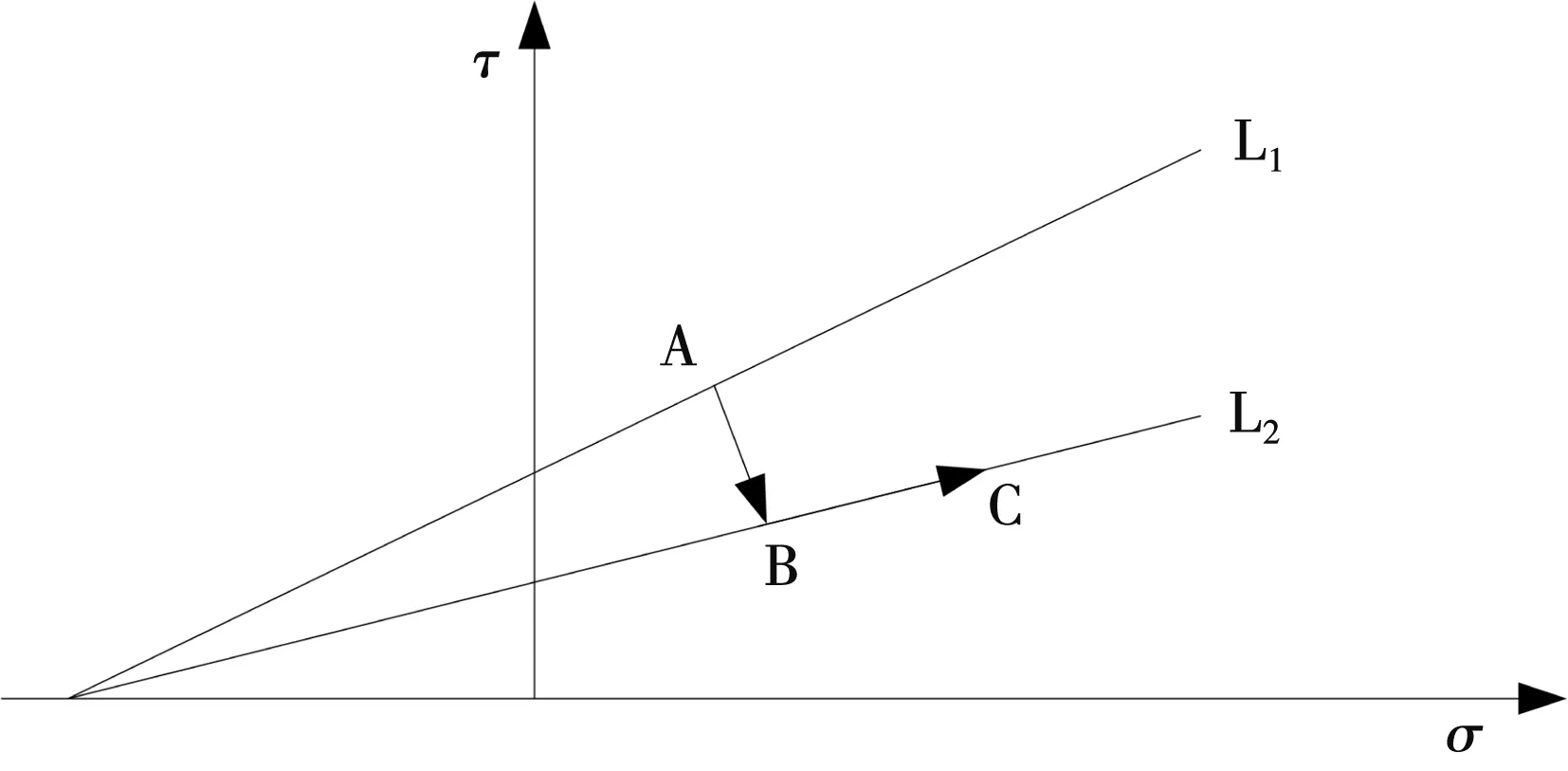
图2 迭代计算中应力变化图

在图1中，支护的屈服面L1的强度在降低后，其参数则变为L2。而在屈服面L1上的点A，在强度降低时则修正到L2上的点B，而后续迭代则会令点B沿L2进行移动，如点C。在迭代过程中，强度参数会出现折减，导致屈服面跟随迭代过程出现变化，使计算收敛性变差，引出需要调整其中的荷载乘子，本文将其设为m，并作为应力调节过程中的荷载比例，并根据比例来拟定对于强度参数的实际折减量，将处于屈服面L1上的应力进行修正，调整后的强度实际整理值则为：

(8)

其中，下标的A、B、C均为应力对应的点。经过迭代计算后，即可得出不同应力下支护的应力状况，从而根据拟定的应力要求，得出相应的安全系数。

2 实验论证分析

为了验证设计的安全性有限元分析方法的可行性，设计实验，采用某地水库大坝工程的基坑支护进行安全性有限元分析，并与文献[1]、文献[7]及文献[9]中的有限元分析法进行对比，判断有限元分析后的数据准确性，再依据数据准确性得出该方法的安全性和有效性。

2.1 工程介绍

实验中的水库大坝控制流域面积为331 km2，库容为836×104m3。在工程开挖中，需要对被挖表面土体剥离14 721 m3，对深处卵石土体的开挖则需要剥离31 040 m3，对石方的开挖中剥离133 211 m3。在坝体基坑开挖中，最深开挖深度为27 m，在最浅深度为12 m。在该工程中，影响支护结构的土层参数见表1。

表1 影响支护结构的土层参数

2.2 实验结果

在对基坑支护的安全性有限元分析中，通常都会提前分析在不同开挖下支护参考点的位移状况，并以此得出对应的安全性。因此在本文实验中，主要对照不同有限元分析方法，对基坑开挖过程中准确预先分析出对应的位移量。其中，该工程的支护短边中点在开挖中的位移见表2。

表2 支护短边中点开挖位移分析

在表2中，分析方法1为本文设计的有限元分析方法，分析方法2为文献[1]中的分析方法，分析方法3为文献[7]中的分析方法，分析方法4为文献[9]中的分析方法。由表2中可以看出，在对不同开挖下的预先分析中，本文设计的有限元分析方法更接近实际数值。

对于支护的长边中点的位移有限元分析结果见表3。

表3 支护长边中点开挖位移分析

在表3的支护长边中点的开挖位移分析中，与表2结果类似，本文有限元分析得出的位移值更接近实际数值，说明本文有限元分析结果更接近实际数值。从安全性分析的角度来说，分析中的数据越接近真实数值，说明分析准确度越高，安全性分析时获得的指标更加准确，由此可证明本文设计的安全性有限元分析方法具有可行性。

3 结 语

本文在有限元分析中，添加了物元描述，以此来降低因基坑土体和支护架之间互斥性对有限元分析结果的影响。实验结果证明，本文设计的安全性有限元分析方法得出的支护位移结果更接近实际施工结果，证明分析方法的可行性。而在本文分析方法中，将深基坑分为多个网格单元进行分析，导致分析时的运算量过大，对设备的占用较为严重。在今后的研究中，将会尝试采用更简捷的分析方法来进行分析。