基于多元非线性回归与BP神经网络模型对土壤水分蒸发量的预测
韦 琦,李思颖,白胤豪,朱鹏飞,胡舒璇,黄品天
(河海大学 a.农业科学与工程学院;b.水文水资源学院;c.环境学院;d.水利水电学院,南京 211100)
0 引 言
研究意义:农田小气候中的环境因子对土壤水分蒸发量有着重要影响,环境梯度CMG表征自然环境条件在不同时间与空间上表现的变化,有效调节温光湿数值对于促进作物蒸腾蒸发,有着重要的研究意义。目前,还未开展基于温度、光照、湿度、环境梯度4者对于土壤水分蒸发量影响的研究,因此掌握4者对于土壤水分蒸发量的影响,对于作物高效用水与蒸腾蒸发有着重要意义。
研究进展:基于环境因子的水分蒸发研究,相关学者已经开展了大量的研究。如马丽丽等研究了水分蒸发量与环境因子、土壤水分蒸发与环境因子之间的关系,结果表明水分蒸发模型为:水分蒸发量=8.369 2+0.037 8*室内平均温度-0.083 9*室内平均湿度+0.004*室内平均光照;土壤水分蒸发模型为:土壤水分蒸发量=-0.388 2+0.008 3*土壤平均温度+0.007 2*室内平均温度+0.002 8*室内平均湿度+0.001 4*室内平均光照[1]。
拟解决的问题:以河海大学江宁校区节水园区大棚内小型气候站在2020年9月27日至2020年11月5日的测量数据为研究对象,利用多元回归分析、BP神经网络两种预测模型对其进行预测,使用剩余预测偏差进行检验,选择预测精度高的模型,研究结果对控制农田小气候对土壤水分蒸发量的影响、促进作物高效用水有重要的指导意义。
1 研究地概况
试验在河海大学江宁校区节水园进行,实验区位于N31°86′,E188°60′,属于亚热带温润气候,冬冷夏热,四季分明。年平均降雨量1 021 mm,年平均蒸发量900 mm,平均湿度81%。年均日照时数2 212.8 h,日照时数百分率约50%[2]。
2 研究方法
2.1 试验设计
试验在河海大学江宁校区节水园进行,在温室大棚内设置小型气象站,大棚内栽种有番茄、辣椒等作物。小型气象站平均30 min记录一次数据,数据包含温度、光合有效辐射、湿度、土壤含水率等。试验数据范围为2020年9月25日至2020年11月7日,通过电脑下载监测数据,利用Excel存储文件。
2.2 数据处理
2.2.1 数据统计分析
测定数据的分析与计算通过SPSS 24.0和MATLAB 2019 a完成。
2.2.2 环境梯度CMG模型构建
CMG计算公式:
(1)
其中:GAT为气温归一化数值;GRH为湿度归一化数值;GH为光合有效辐射量归一化数值。
2.2.3 多元非线性回归模型构建
多元非线性回归分析的主要目的是预测。本研究借助多元非线性回归模型,由气温、湿度、光合有效辐射量、环境梯度的最优组合来预测土壤水分缺失量。模型公式:
y=a+b*x1+c*x2+d*x3+e*x4+f*x1*x2+…+k*x3*x4
(2)
2.2.4 BP神经网路模型构建
人工神经网络(artificial neural networks,ANNs)是一种模仿人脑神经网络行为特征,进行分布式并行信息处理的数学模型。人工神经网络的拓扑结构包括输入层、隐含层和输出层,每层均由称为节点的元素组成。其中BP神经网络(back propagation artificial neural network, BPANN)是 1986 年由 Mccelland 等提出的按误差逆传播算法训练的多层前馈网络,也是目前应用最广泛的神经网络模型之一。BP神经网络是监督式学习算法,其学习过程由信号正向传播与误差反向传播两个过程组成。信号的正向传播过程是指将各要素信息由输入层传至隐含层最后至输出层,若输出层的实际输出与期望输出不等,则转到误差的反向传播阶段。此过程一直进行到网络输出误差减少到可接受的程度或进行到预先设定的学习时间和学习次数为止。根据Kolmogorov定理,具有1个隐层的3层BP神经网络能在闭集上以任意精度逼近任意非线性连续函数。网络拓扑结构见图1。

图1 神经网络拓扑结构图
假设BP神经网络的输入矢量为x∈Rn,其中x=(x0,x1,…,xn-1)T,输入层到隐含层的权值为wij,阈值为θj,隐含层有1个神经元,则输出量为:
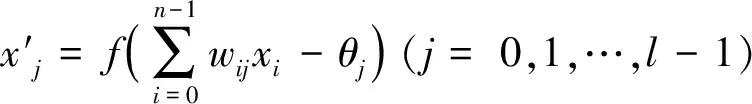

(4)
式中:激活函数f(x)为单极性函数,连续且可导,根据应用需要,f(x)可为双极性函数。
BP神经网络算法性能评价通过网络训练数据和实际数据的差值大小来衡量,计算公式为:
(5)
则其调整值为:
(6)
式中:p为训练集向量数据索引;k为输出向量数据索引;tpk为期望输出向量;Zpk为输出层向量;η为学习率[3]。
2.2.5 模型模拟精度检验
通过剩余预测偏差、判定系数指标来判定模型的精度。剩余预测偏差(Residual Predictive Deviation,RPD)为:
(7)
其中:OBSi为实测数据(observation data);SIMi为模型模拟数据(simulation data);n为观测样本数;ξ为样本标准差。
当RPD>2时,模型预测能力比较强;当2>RPD>1.4时,模型预测能力属于中等水平;当RPD<1.4时,模型无法对数据进行预测。模型判定系数R2为:
(8)
当R2越接近1时,表示模型的参考价值越高[4]。
3 结果与分析
3.1 多因素对土壤水分蒸发量影响的多元回归分析
通过大棚内环境气象资料(温度、光合有效辐射量、湿度、环境梯度)进行回归分析,得到如下的数量关系式:
(9)
式中:y为土壤水分蒸发量;x1为环境梯度CMG;x2为光合有效辐射量;x3为温度;x4为湿度。
利用回归公式对任选的31个样本进行预测,并与真实预测值比较,得到结果见图2。

图2 多元非线性回归所得土壤水分蒸发量预测值与真实值比较
由比较结果可知,预测值与真实值之间有微小误差,可以接受该回归模型结果。
3.2 BP神经网络预测结果
取394个样本进行神经网络分析,选取70%数据作为样本训练集——用于模型拟合的数据样本;选取15%数据作为样本验证集,用于寻找最优的网络深度,决定反向传播算法的停止点或者在神经网络中选择隐藏层神经元的数量;选取15%作为测试集——用于评估最终模型的泛化能力。在此次分析中,选取神经元的个数为10个,网络结构图见图3。
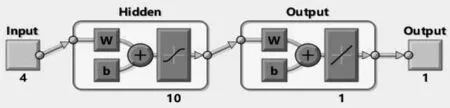
图3 神经网络结构图
选取的训练算法为Levenberg-Marguardt algorithm,它能提供非线性最小化的数值解。训练结果见图4、图5。

图4 训练结果(显示在训练31次后呈现最优)

图5 各组拟合优度
根据拟合结果可以发现,拟合优度接近70%,训练结果可以接受。
同样任选31个样本进行预测,并与真实值比较,所得结果见图6。

图6 BP神经网络对土壤水分蒸发量的预测值与实测值对比
3.3 模型模拟精度比较结果
利用MATLAB 2019a进行精度计算,得到多元非线性回归方程预测结果的剩余预测偏差RPD=1.83;BP神经网络预测结果的剩余预测偏差RPD=2.14,且BP神经网络模型判定系数R2更接近于1。所以,BP神经网络预测结果更加准确。
4 结 论
通过研究得出以下结论:多元非线性回归与BP神经网络均可以预测CMG、温度、湿度、光合辐射量的影响,相比之下,BP神经网络的预测能力更好,多元非线性回归在预测范围端点处出现龙格现象,使得预测结果与真实结果有所偏差。
应用BP人工神经网络的优势在于可以模拟人们了解较少或模糊性较大的小气候系统,这些是传统的回归模型所不能够实现的,是对传统回归模型的重要补充。应用时注意BP神经网络模型的训练数据只能是采集于特定环境、特定时间,往往是通过反复的训练来确定网络的结构和各种参数,并且需要大量的样本量来保证所求取参数的可靠性。

