某水电站厂房下部结构抗振分析
盛健挺,于 奎,孙忠园,贾晶玺,梁江晟
(1.黑龙江大学水利电力学院,哈尔滨 150080;2.黑龙江省水利水电勘测设计研究院,哈尔滨 150080)
0 引 言
在水电站厂房的结构计算中,尤其要考虑到振动带来的危害,这是由于发电机、水轮机转子质量的不平衡、导叶叶片与转轮叶片在水流的激振中互相交会、水流状态的不断变化引起蜗壳及压力管道内水锤波的影响、尾水管内不断发生的涡流变化的影响、发电机组产生的不平衡磁拉力等所引起的。风罩是机墩上部的薄壁圆筒结构,其顶部与发电机层楼板相连,风罩在受到机墩传来的振动时,也会将振动作用传递给楼板,那么楼板给风罩的约束对风罩以下的整体结构具体产生多大程度的影响还不清楚[1-5]。
机墩的下面连接着蜗壳的外围混凝土,这部分的混凝土通常称其为蜗壳顶板,蜗壳顶板应该浇筑多大的厚度,使其对于连接在其上的机墩风罩整体结构的自振特性的影响达到最小[6],关于这方面的研究目前还很少,文章将结合国内某一发电站一一探讨以上问题。
1 计算方法
1.1 理论计算
机墩是发电机组的支承结构,其自振频率的验算必不可少,顾鹏飞[7]等将机墩的自振频率的计算简化为单自由度体系的振动,经过许多学者的论证,在空间上没有考虑蜗壳尾水管等的相互作用带来的影响,所得结果不够精确,但由于在一定程度上能够反应一定的结果,故在一些中小型电站中仍然适用,规范[8]上仍然采用这个算法。
1.2 数值分析
求解结构的自振频率的另一种方法是模态分析法,模态分析是研究结构动力特性的一种方法,现在广泛应用于工程振动领域。模态是指机械结构固有振动特性,每一个模态都有特定的固有频率、阻尼比和模态振型,分析这些模态参数的过程称为模态分析。有限元的模态分析就是建立模态模型并进行数值分析的过程。模态分析的实质就是求解具有有限个自由度的无阻尼及无外载荷状态下的运动方程的模态矢量[9](因结构的阻尼对其模态频率及振型的影响很小,可以忽略),系统的无阻尼自由振动方程的矩阵表达式为:
[M]{ü}+[K]{u}={0}
(1)
对线性结构下的系统,式(1)中[M]、[K]都是实数对称矩阵,方程具有下列简谐运动形式的解,其形式为:
{u(x,y,z,t)}={H(x,y,z)}eiwnt}
(2)
式中:{H(x,y,z)}为位移矢量的幅值,它定义了位移矢量{u}的空间分布;kn为简谐运动的角频率。将式(2)代入式(1)后,得到下列与{H}和kn有关的方程:
[K-kn2M]{H}exp(iknt)={0}
(3)
式(3)在任何时刻t均成立,故去除含t的项,得到:
[K-kn2M]{H}={0}
(4)
式(4)成为典型的实特征值问题,{H}有非零解的条件是其系数行列式的值为零,即:
|K-kn2M|=0
(5)
或
|K-λM|=0
(6)
式中:λ=kn2。式(6)左边为λ多项式,可以解出一组离散根λi(i=1,2,…,n),将式(6)代回(4)式可得对应的矢量{Hi}(i=1,2,…,n),使得下式成立:
[K-λiM]{Hi}={0}i=1,2,…,n
(7)
式中:λi称为结构系统的第i个特征值,{Hi}称为对应的第i个特征矢量。
2 某水电站厂房概况
某水电站厂房设有4台水轮发电机组,单机容量2150KW, 型号为SF2150-14/2150,水轮机的型号为ZD1127-LJ-130,其中风罩上部与发电机层楼板整体连接,下部与机墩的环向相连,连接形式为整体浇筑的钢筋混凝土结构,风罩外壁直径5.2m,壁厚0.5m,为一薄壁圆筒结构,在主引出线和中性点引出线各开有一个孔洞,包括进入孔一共三个孔洞。机墩在蜗壳顶板上部,采用大体积混凝土厚壁圆筒结构,内部直径1.56m,外直径5.2m,高度为1.12m,下机架基础板以及定子基础板都为4个,基础板材质采用Q235A钢材。
3 结构的模态分析计算
3.1 ANSYS三维有限元软件
ANSYS软件是融结构、流体、电场、磁场、声场分析于一体的大型通用有限元软件,ANSYS的模态分析可以对有预应力的结构进行模态分析和循环对称结构模态分析,本次的分析计算采用这一软件。
3.2 模态计算
计算模型选为机墩风罩蜗壳顶板,由于是混凝土整体浇筑,故三者接触方式选为共节点,蜗壳顶板底部固定,对模型进行网格划分,单元数11234,节点数41794,主要为6面体,风罩机墩蜗壳顶板整体网格模型,见图1。

图1 风罩机墩蜗壳顶板整体网格模型
用上述模型求得的前7价的自振频率的结果,所取模型模态分析计算结果,见表1。

表1 所取模型模态分析计算结果
3.4 楼板的约束作用
以上模型未考虑楼板对风罩的约束作用,所以下面考虑在风罩顶部施加一个法向约束作为楼板对风罩的简支作用,再来分析其对于整体自振特性的影响,楼板约束下模型前7阶自振频率,见表2。
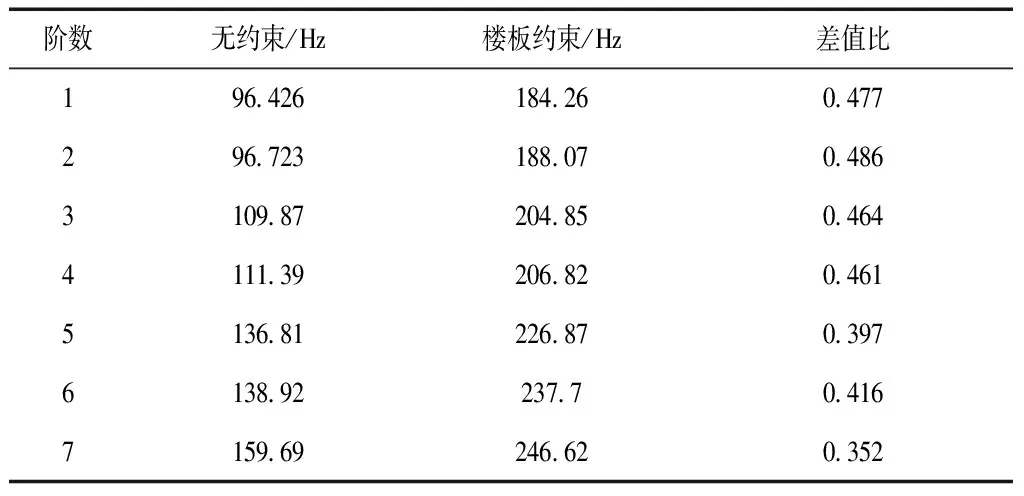
表2 楼板约束下模型前7阶自振频率
模态分析的结果发现前6阶风罩部位产生的位移较大,表现为风罩的自振特性,第7阶开始,机墩部位也参与较为明显的位移变化,由下图对比可以看出第7阶风罩机墩蜗壳顶板组合结构发生整体的运动[10-11]。1阶模态分析位移结果,见图2。

图2 1阶模态分析位移结果 图3 7阶模态分析位移结果
3.3 共振校核
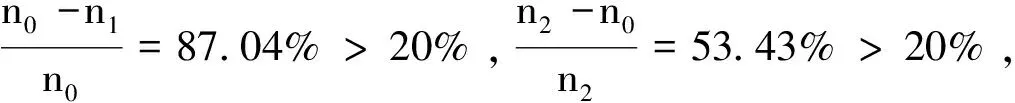
由此可知,楼板对风罩的约束作用不可忽视,可以有效的提高风罩的刚度。
3.5 蜗壳顶板对风罩机墩的自振频率的影响
3.5.1 不考虑蜗壳顶板
若不考虑蜗壳顶板的作用,将机墩底部完全约束,风罩顶部自由,这时得到机墩的自振频率的结果,不考虑蜗壳顶板得到的自振频率,见表3。

表3 不考虑蜗壳顶板得到的自振频率
此结果与表1进行对比可知,每阶的频率均有所上升,说明考虑蜗壳顶板的作用会降低风罩机墩整体的刚度,因为系统的固有频率随着质量的增加而减少,但蜗壳顶板对于风罩机墩的刚度究竟会产生多大的影响需要进一步的分析。
3.5.2 蜗壳顶板不同厚度的整体结构自振频率
仅从蜗壳顶板的厚度开始考虑,取蜗壳顶板厚度分别为0.5m,1m,1.47m(此电站厂房的蜗壳顶板厚度),2.0m,2.5m,3.0m,5.0m,将所得结果列成表格形式如表4。考虑不同厚度的蜗壳顶板得到的自振频率,见表4。

表4 考虑不同厚度的蜗壳顶板得到的自振频率
将表格数据绘成曲线图,考虑不同厚度的蜗壳顶板得到的自振频率,见图4。
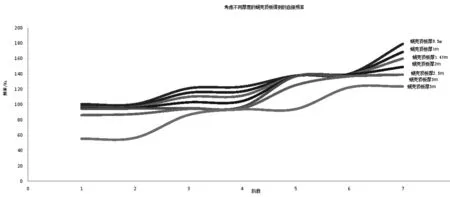
图4 考虑不同厚度的蜗壳顶板得到的自振频率
1)分析图表可以发现,随着蜗壳顶板厚度的增加,风罩机墩蜗壳顶板整体的自振频率逐渐降低,说明增加顶板厚度,不利于整体刚度。
2)对蜗壳顶板厚度为5m的情况不作任何量的对比,仅仅作为视觉上参照。可以发现,蜗壳顶板厚度在0.5-2.5m时,其图像呈现出一定的规律,均表现为:随着顶板厚度增加,1、2阶的自振频率保持不变,3、4阶的自振频率发生均匀减少,5、6阶的自振频率基本不变,第7阶的频率开始均匀下降,
3)在蜗壳顶板厚度为2.5m的情况,第7阶的频率下降到与第6阶的值接近相等;当蜗壳顶板厚度为3m时,相比较顶板厚度为2.5m的情况,第1、2、5阶频率显著下降,变化幅值分别为8.41Hz、7.11Hz、11.65Hz,第3、4、6、7阶频率基本保持不变。
4)由此说明,仅从风罩机墩蜗壳顶板构成的整体结构抵抗水轮发电机组产生的振动方面考虑,当蜗壳顶板厚度>2.5m时会对整体刚度影响相对较大,在本工程中蜗壳顶板厚度应该≤2.5m,该电站取蜗壳顶板厚度1.47m,显然满足要求。
4 结 语
1)楼板对风罩的约束至关重要,可以有效提高风罩的刚度,增加其抗振能力。
2)考虑蜗壳顶板会减少系统的自振频率,增加蜗壳顶板的厚度相当于增加系统质量,所以模型的自振频率大小随蜗壳顶板厚度增加而变小。
3)蜗壳顶板的厚度在0.5-2.5m时,模型的自振频率随着模态阶次的增加发生规律性的变化,表明蜗壳顶板的厚度在此范围内对整体刚度的影响较小。
4)蜗壳顶板的厚度>2.5m时将较大程度影响该水电站风罩机墩蜗壳顶板组合结构的自振频率,故安全起见,本电站蜗壳顶板厚度不应该超过2.5m,本电站蜗壳顶板厚度取1.47m,从自振特性方面考虑满足要求。

