噪声非高斯条件下基于最大相关熵准则的容积滤波算法

张敬艳，修建娟，董 凯,2

(1.海军航空大学 信息融合研究所， 山东 烟台 264000；2.中国电子科学研究院，北京 100041)

1 引言

随着现代雷达技术的快速发展，多普勒雷达在侦察监视、火力控制等领域得到了广泛应用[1-2]。多普勒雷达能够获得目标相对雷达的径向速度信息，利用此信息能够更加精确地跟踪目标，并为后续火力打击提供支持。文献[3]首先处理位置量测，然后利用位置滤波值获得径向速度量测的伪线性描述，通过Kalman滤波更新目标的运动状态。由于不敏Kalman滤波(UKF)即无迹Kalman滤波对非线性不敏感，文献[4]首先对距离量测和径向速度量测进行去相关处理，然后通过Kalman滤波和UKF依次处理线性位置量测和非线性径向速度量测，获得对目标状态的估计，并分析了不同的相关系数对估计结果的影响。文献[5]利用转换多普勒量测Kalman滤波分别从转换多普勒量测和转换位置量测获得非线性伪状态估计，并通过静态最小均方误差准则融合上述2种估计值，获得对目标状态的最终估计。以上方法均采用转换量测方式进行状态滤波，由于量测非线性可通过不敏变换等手段进行处理，文献[6]提出了一种直接不敏卡尔曼滤波算法，并对其性能进行了分析。

上述算法均假设量测噪声服从高斯分布，但是，在实际应用中，量测噪声通常是非高斯的[7]，上述算法难以获得较高的状态估计精度。虽然粒子滤波能够较好地解决量测非高斯问题，但是其计算量较大，很难实现对状态的实时估计[8]。从信息论的角度出发，文献[9]分析了信息熵在处理非高斯信号时的性质及应用。针对线性非高斯系统，文献[10]提出了一种最大相关熵Kalman滤波算法，实验结果表明该算法能够有效处理量测噪声非高斯条件下的线性状态滤波问题。

由于多普勒雷达量测非线性，可考虑利用容积变换[11]近似滤波过程中出现的高斯加权积分；同时，由于量测噪声非高斯，可利用最大相关熵准则获取估计误差的高阶矩，从而提高目标状态估计精度。综合上述分析，在噪声非高斯条件下，首先利用容积变换获得伪量测矩阵，并根据统计误差线性传递模型对量测方程进行近似处理；然后基于最大相关熵准则构造代价函数，并通过固定点迭代更新目标估计状态，提出了一种基于最大相关熵准则的容积滤波算法MCCKF，仿真实验验证了所提MCCKF的有效性。

2 最大相关熵准则

两个随机变量之间的广义相似性可以用相关熵进行度量[10,12]。给定2个随机变量X,Y∈R，其联合概率分布函数为FXY(x,y)，那么二者之间的相关熵可以定义为：

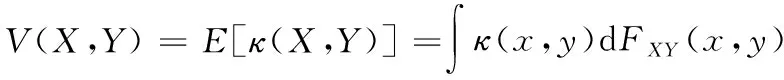
(1)

其中，E表示期望，κ(·,·)表示移位不变Mercer核函数。本文采用高斯核函数进行相关计算，即

(2)

其中：σ>0表示高斯核带宽。对式(2)所示的高斯核函数κ(x,y)进行泰勒展开，并代入式(1)，得到

(3)

从式(3)可以看出：相关熵是误差X-Y偶数阶矩的加权和。在核带宽σ足够大的情况下，相关熵的大小将由二阶矩决定。

在实际应用中，联合概率分布函数为FXY(x,y)通常未知，只能得到有限的采样数据集合{x,y}。此时，可利用样本平均估计相关熵，即

(4)

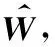
(5)

3 问题描述

考虑二维空间中的匀速直线运动目标，其动态方程为

xk+1=Fkxk+wk

(6)

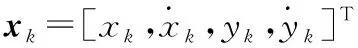
利用多普勒雷达观测目标的运动状态，对应的量测方程为

zk+1=h(xk+1)+vk+1

(7)

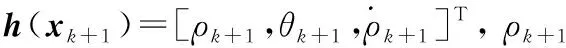
(8)

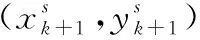
(9)

4 MCCKF算法推导

本节将最大相关熵准则与统计线性回归模型结合，推导了一种用于解决非线性非高斯系统状态滤波的新方法。与最小均方误差估计不同，相关熵考虑了误差的二阶及更高阶矩。因而，在闪烁噪声这类长拖尾非高斯噪声条件下，基于最大相关熵准则能够获得相对更好的状态估计性能，仿真实验部分对此进行了验证，此处不再赘述。与CKF等Kalman类滤波器相似，MCCKF也分为时间更新与量测更新两部分，具体如下：

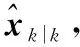
(10)

(11)

根据容积求积分规则，对预测协方差Pk+1|k进行Cholesky分解，获得相应的状态采样点

(12)

(13)

经量测函数h(·)传递后的容积采样点为

Zi,k+1|k=h(χi,k+1|k)

(14)

量测的一步预测值可以表示为

(15)

进一步，状态-量测交叉协方差可以表示为

(16)

因此，伪量测矩阵Hk+1可以表示为

(17)

根据统计误差线性传递模型，量测方程(7)可以表示为

(18)

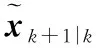
(19)

(20)

dk+1=Wk+1xk+1+ek+1

(21)

其中，

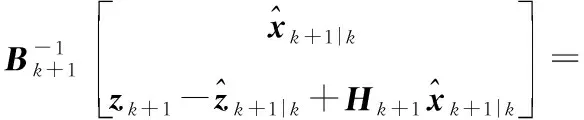
(22)

(23)

(24)

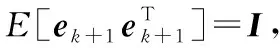
(25)

(26)

对JL(xk+1)求导数，并令

可以得到

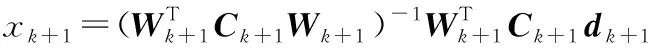
其中，

将式(22)和式(23)代入式(27)，得到

(28)

(29)

利用矩阵求逆引理，并将式(28)和式(29)代入式(27)，得到

(30)

其中，

(31)

(32)

对应的估计误差协方差可以表示为

(33)

从式(21)、式(27)和式(30)可以看出，式(30)实际上是一个关于xk+1的固定点方程，即

xk+1=g(xk+1)

(34)

因此，可利用固定点迭代算法获得式的解，即

(35)

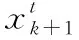
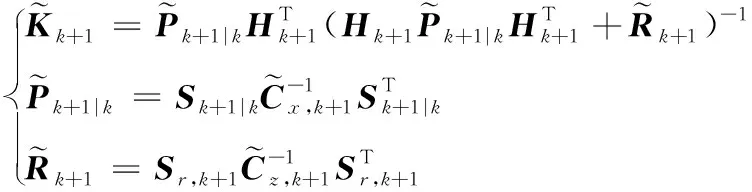
(36)

(37)

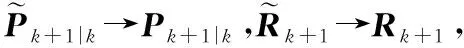
综上所述，通过引入最大相关熵准则，并利用固定点迭代更新目标的状态估值，MMCKF可有效捕获量测中的非高斯噪声信息，实现滤波性能的提升，仿真实验对此进行了验证。MCCKF算法的具体流程如下：

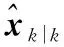
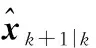
(2) 利用式(12)～式(17)计算伪量测矩阵Hk+1，并构造式所示的统计误差线性传递方程；

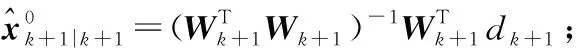
则执行步骤(6)；反之，则继续执行步骤(4)，直至前后两次迭代估计值满足上述收敛条件。

(6) 更新估计误差协方差

5 仿真实验

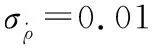
5.1 高斯量测噪声

假设量测噪声服从高斯分布，即vk+1～N(0,Rk+1)，得到各算法的估计结果如下：

从图1和图2可以看出：在高斯噪声条件下，EKF、UKF和CKF的估计误差相对较小，而所提MCCKF的估计误差相对较大。此外，随着高斯核带宽σ的增加，所提MCCKF算法逐渐逼近CKF等的状态估计性能。从图 3可以看出：UKF和CKF的状态估计一致性相对较高，而EKF、MCCKF类算法的估计一致性相对较差。

图1 位置均方根误差曲线

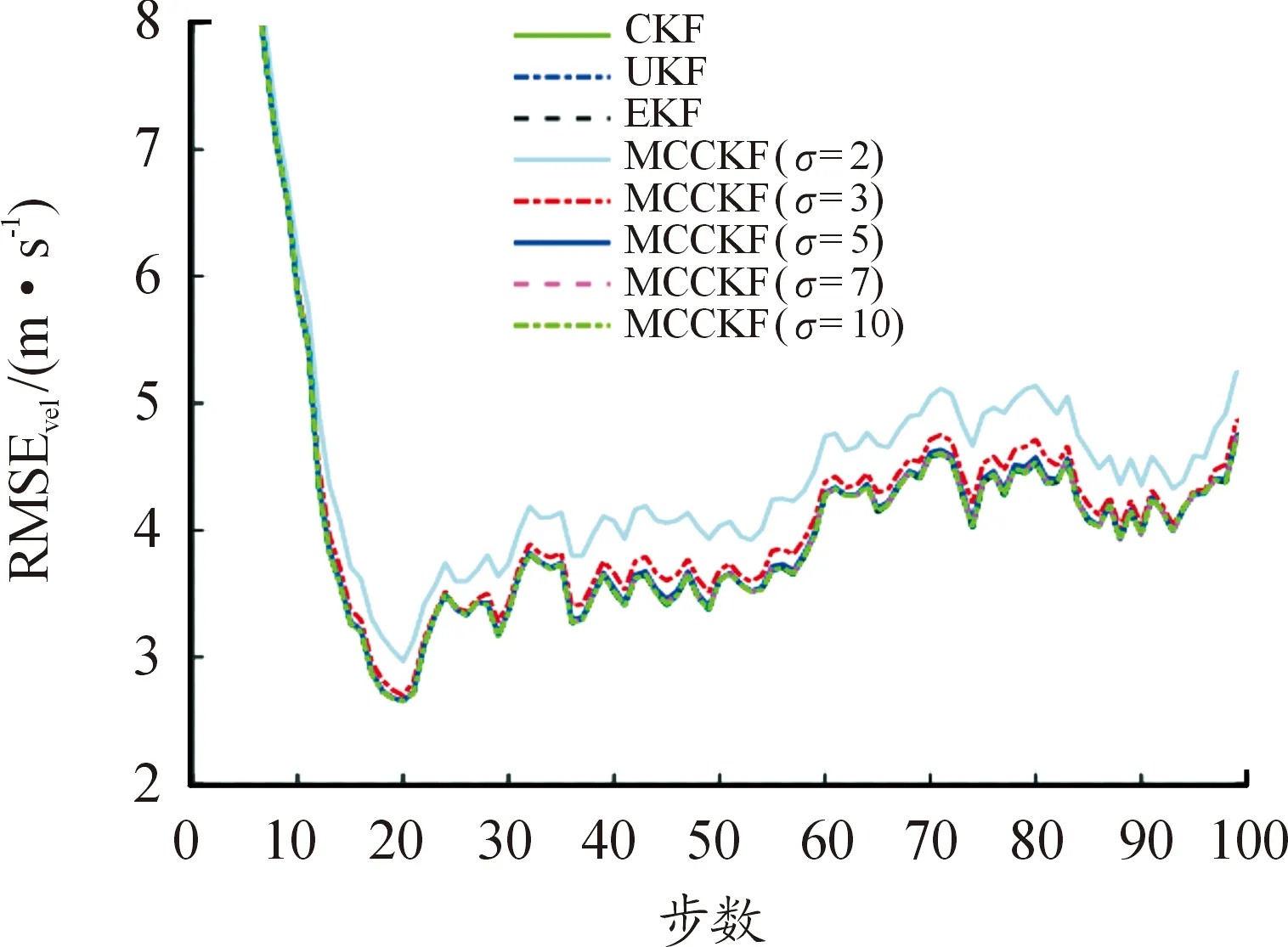
图2 速度均方根误差曲线

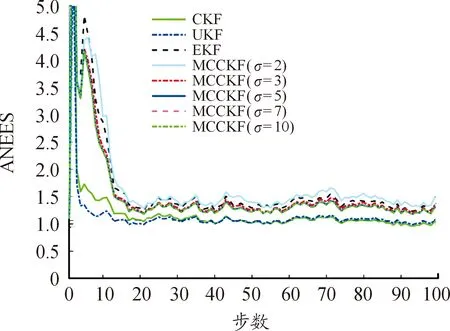
图3 平均归一化估计误差平方曲线

进一步，从表1可以看出：经过少量的迭代，所提MCCKF算法便可实现收敛。从表2可以看出：随着高斯核带宽σ的增加，MCCKF的估计误差逐渐减小，并逼近CKF等的估计结果。

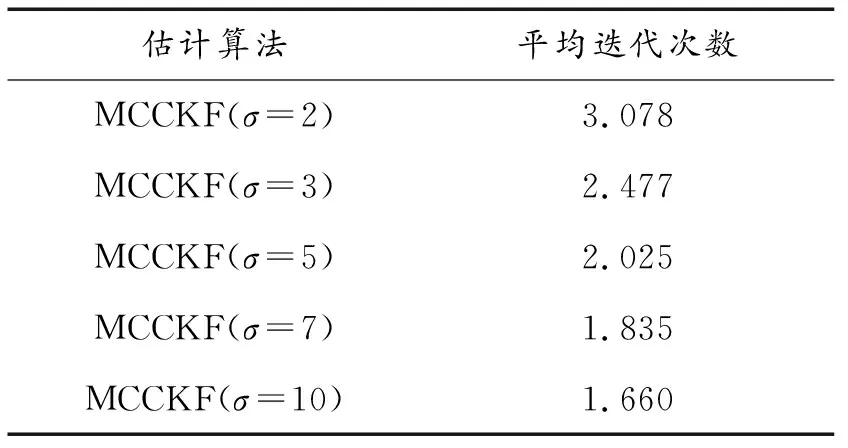
表1 平均迭代次数随带宽σ的变化

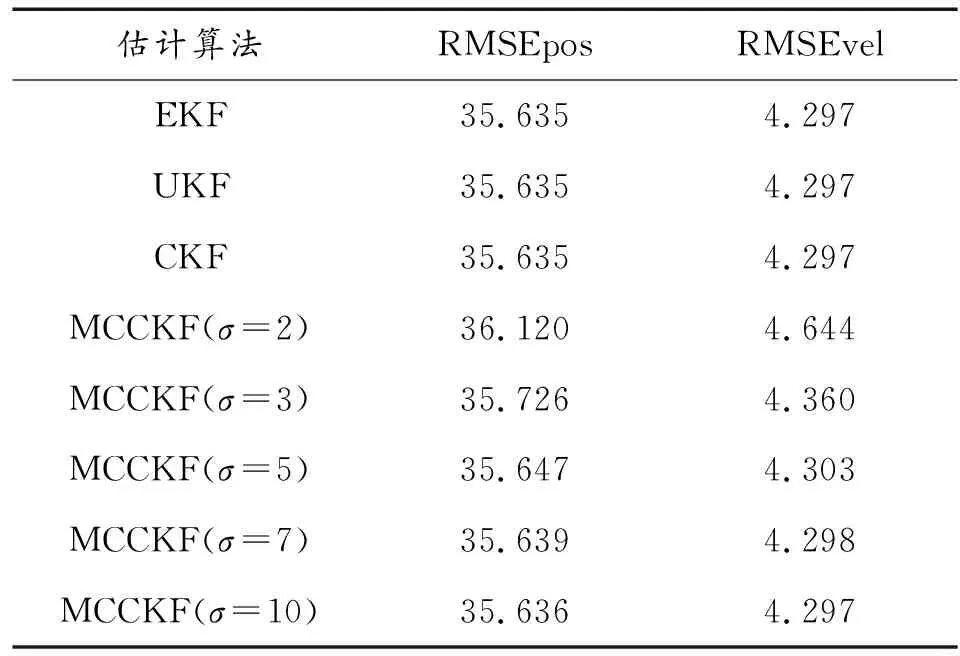
表2 高斯噪声条件下的估计误差

5.2 非高斯量测噪声

假设量测噪声服从非高斯分布，即vk+1∶0.95N(0,Rk+1)+0.05N(0,50Rk+1)，得到各算法的估计结果如图4～图6所示。

从图4可以看出，在非高斯噪声环境下，与CKF等Bayes估计相比，MCCKF算法的位置估计误差相对较小，且在σ=2时估计误差最小。与图4所示的结果相似，在图5中，除少数时刻外，MCCKF算法的速度估计误差较CKF等Bayes估计小。从估计一致性来看，图6所示的结果表明：从k=20开始，MCCKF算法的ANEES基本落在置信区间内，而CKF等大部分时刻落在置信上界上方。因此，MCCKF算法的估计一致性相对较好。

图4 位置均方根误差曲线

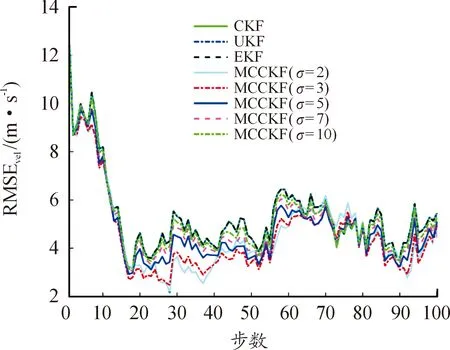
图5 速度均方根误差曲线

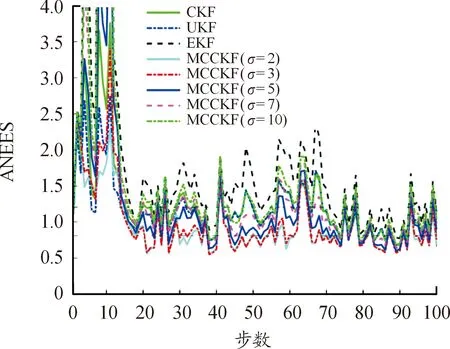
图6 平均归一化估计误差平方曲线

进一步，表3比较了平均迭代次数与核带宽σ的关系，结果表明：经过少量的迭代，MCCKF便可实现收敛，从而不会造成计算量的大幅增加。表4比较了各算法的平均位置和速度估计误差，可以看出，MCCKF的位置和速度估计误差相对较小，且随着高斯核带宽σ的减小，估计误差也逐渐减小，与高斯环境下的结果相反。因此，在高斯噪声环境下，为获得良好的状态估计结果，应选择较大的核带宽σ，而在非高斯噪声环境下，应选择较小的核带宽σ，以捕获误差的高阶矩信息，从而实现对目标状态的高精度估计。

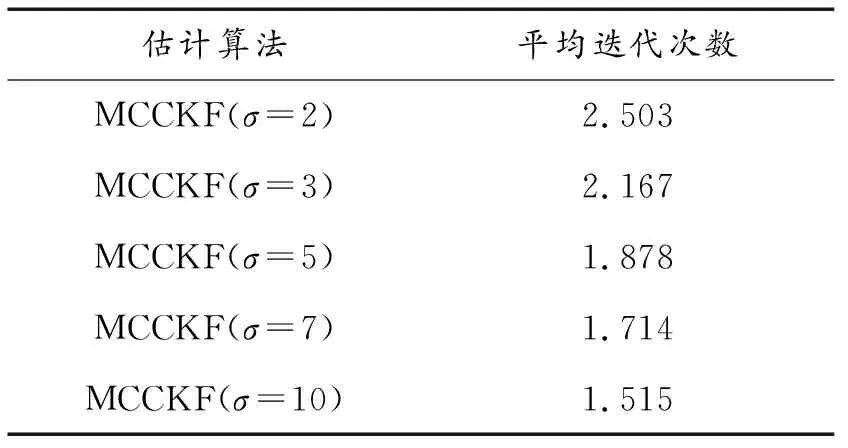
表3 平均迭代次数与带宽σ的关系

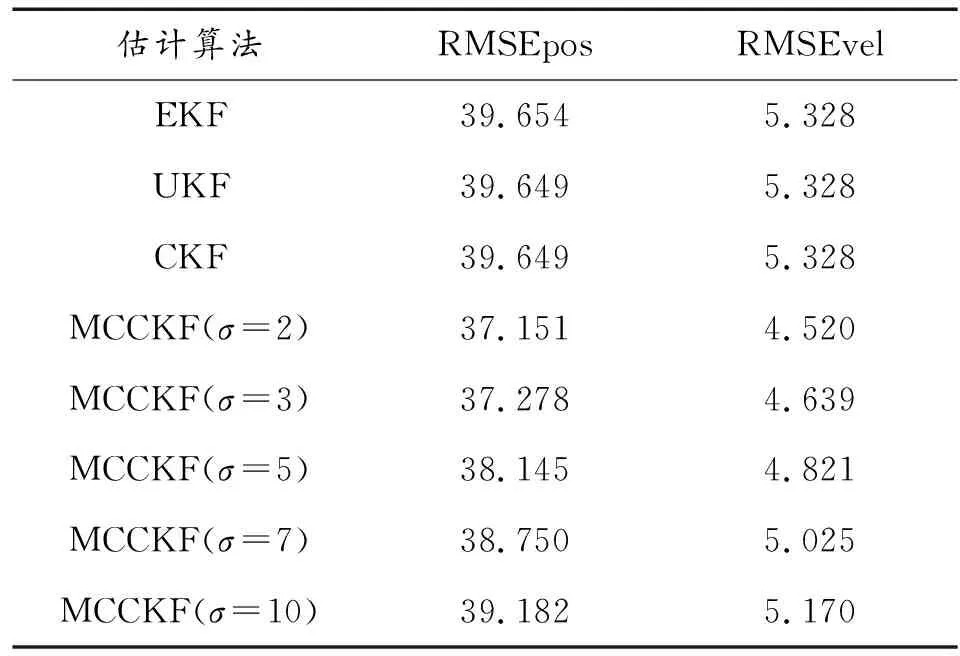
表4 非高斯噪声条件下的估计误差

所提方法考虑了估计误差的高阶矩，的确带来了计算成本的增加，从而造成计算量比CKF大。但是，实验结果证明：经过少量(大约2次)固定点迭代，所提算法便可实现收敛，并且获得相对较高的估计精度。因此，与CKF算法(不需要固定点迭代)相比，计算成本不会显著增加。论文针对所提MCCKF算法在不同高斯核带宽条件下的迭代次数进行了比较，随着高斯核带宽的增加，收敛所需迭代次数逐渐减少，并不是说算法的迭代次数比已有算法更少了。

6 结论

针对舰载多普勒雷达在非高斯量测噪声环境下的非线性状态滤波问题，基于最大相关熵准则和固定点迭代更新策略，提出了一种基于最大相关熵准则的容积滤波算法MCCKF。仿真结果表明：在量测噪声非高斯条件下，经过少量的固定点迭代，MCCKF能够获得较已有CKF等Bayes方法更高精度的状态估计结果，为解决多普勒雷达非线性非高斯状态滤波提供了一种新的解决思路。