考虑燃料消耗均衡性的低轨通信星座在轨星座构型重构方法研究

李玖阳，胡敏，王许煜，李菲菲，徐家辉

1. 中国人民解放军63723部队，忻州 036300 2. 航天工程大学，北京 101416 3. 中国人民解放军32024部队，北京 100000

1 引言

低轨通信卫星相较于中高轨通信卫星具有传输损耗小、通信时延低、发射成本低等优点，由低轨通信卫星组成的低轨通信星座在交通、能源等领域得到广泛应用[1-2]，例如铱星、全球星和Starlink等。低轨通信星座在轨运行过程中，星座的服务性能受星座中卫星可靠性的影响， 若出现失效卫星，需要启用备份星、发射新卫星或者调整已有卫星，改善或者修复星座的工作性能[3]。

备份星在轨过程中一直处于损耗状态，随时可能发生故障，替换失效卫星的计划不容易事先确定，而地面发射备份卫星响应速度较慢。因此，调整剩余卫星工作轨道进行星座重构，具有反应迅速、快速降低失效影响的优点[4]。在轨重构过程中，需要多颗卫星进行机动，重构方案可能会使不同卫星机动消耗能量差别较大，从而造成星座中各卫星能量消耗不均衡，使某些卫星寿命下降过快，影响星座的长期稳定运行。为了解决上述问题，需要将燃料消耗均衡性作为衡量在轨重构方案的重要指标。

近年来，空间竞争逐渐加剧，对星座自身的弹性和稳定性要求越来越高，国内外学者对星座的在轨重构展开研究，并取得了一定的研究成果。张雅声[5]等人针对不同的星座构型，以最短时间内最小能量消耗为目标，对调整相邻卫星策略、均匀相位策略和均匀星座策略展开了研究，Appel[6]等人利用基于邻域极值算法和一阶梯度算法的耦合算法来进行星座重构优化，该方法可以考虑不同卫星的条件限制，不再局限于几种策略，使星座重构更加灵活，Sung等人[7]采用遗传算法、模拟退火和最速梯度法，对对地侦察星座在区域和全球侦察两种模式下进行了星座重构优化分析，对比发现遗传算法较优，但这些算法均为单目标优化算法，无法满足星座重构中的多目标优化需求，Fakoor等人[8]采用兰伯特转移的方式进行星座重构，并使用粒子群算法求出最优解，该方法的优点是重构时间短，卫星初始轨道与目标轨道之间不存在共面性、共轴性和公共点等限制，但缺点是燃料消耗量大，降低星座使用寿命，Ciara等人[9]将小推力机动应用在星座重构过程中，使用较小的速度增量达到了重构效果。

本文首先针对低轨星座在轨重构进行了理论分析，得出了全球平均覆盖率、燃料均衡性、重构总时间和总速度增量4个重构指标和抬升轨道高度的机动方式，而后根据MOEA/D算法和在轨重构的特点建立了优化模型，最后通过仿真试验得出在轨重构优化结果。

2 低轨星座在轨重构理论分析

2.1 重构指标

(1)全球平均覆盖率

覆盖性能是卫星通信星座系统在需要的时间和空间上动态集中所需卫星容量的能力[10-12]。覆盖率是一种有效衡量通信星座覆盖性能的重要指标，具体可按星座的覆盖重数等级衡量，如单星覆盖率和多星覆盖率等。

针对低轨通信星座的全球覆盖性能，提出全球覆盖率指标。按照经纬度，将全球划分为12×24的网格，计算星座对每个网格在一定时间内的平均覆盖重数，而后将满足覆盖重数要求的网格数除以总格数即为全球平均覆盖率，如式(1)所示。

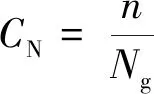
(1)

式中：n为满足覆盖重数要求的网格数;Ng为网格数。

(2) 燃料消耗均衡度

为了降低发射成本，低轨通信星座卫星逐渐向小型化发展，各卫星自身携带的燃料有限。同时，整个星座的寿命和每颗卫星的寿命有关，在星座运行中期，各卫星剩余燃料较不均衡，在出现卫星失效需要重构恢复性能的情况下，若某些卫星燃料被过度消耗，则可能会造成这些卫星提前耗尽寿命，从而影响整个星座的寿命和服务性能。因此，在重构过程中需要考虑燃料均衡性这一指标。

衡量卫星燃料消耗的指标为卫星机动的速度增量，星座在轨重构过程需要多颗卫星机动，而速度增量的方差则可作为衡量这一指标的标准，如式(2)所示[13]。

(2)

(3)重构总时间和总速度增量

随着互联网的发展，对低轨通信星座的通信时延、带宽等提出了更高的要求，当星座遭遇突发状况出现多颗卫星失效影响性能时，需要通过重构尽快恢复性能，同时需要尽量少的能量消耗来保证星座的后续服务性能和寿命。

为了满足上述需求，提出的指标为重构总时间和总速度增量，重构总时间是指参与重构的各卫星机动时间之和，如式(3)所示。

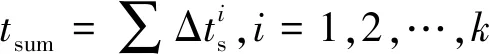
(3)

重构总速度增量是指参与重构的各卫星机动过程中速度增量之和，如式(4)所示。

(4)

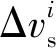
2.2 两重构机动方式

星座重构即对能正常工作的卫星进行轨道机动，改变卫星站位，尽可能的恢复星座原有性能的优化过程。具体可分为相位调整[14]和轨道高度调整等方式。

低轨卫星轨道高度低，对地覆盖面积小，在低轨星座出现多颗卫星故障性能损失的情况下，调整相位的方式效率较低且效果较差，难以满足需求，因此，可通过抬升剩余的某些卫星轨道高度的方式对原有星座进行重构，达到恢复星座原有性能的目的，如图1所示。

图1中采用霍曼转移的机动方式，所需的时间和速度增量如式(5)所示[15]。

图 1 抬升轨道机动方式Fig.1 Lifting orbit maneuver

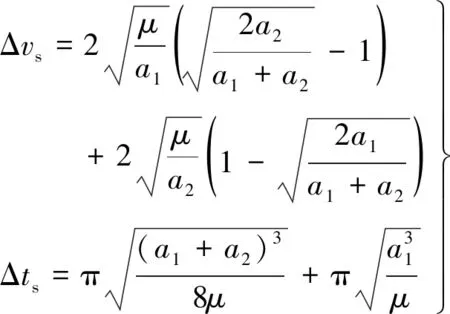
(5)

式中：Δvs,Δts分别为转移所需速度增量和时间;μ为地球引力常数;a1,a2为初始轨道和目标轨道的半长轴。

3 基于MOEA/D的低轨星座重构方法

多数星座重构采用固定的重构方案，实现了一定的重构效果，但这些方式不一定是最优的。随着低轨星座规模越来越庞大，使用固定的重构方案难以达到最优效果，且由于卫星数目众多，固定重构方案难以寻找。因此，需要采用多目标优化算法实现低轨星座在轨重构。

3.1 编码方式

星座在轨重构过程需要确定参加重构卫星、参加重构卫星轨道高度调整量，其中参加重构卫星需要布尔变量来决定卫星是否参与重构，参加重构卫星为离散变量，轨道高度调整量为连续变量。

针对上述变量情况，需要将算法的基因片段分为两个部分，第一部分代表星座中各卫星参与重构的情况、第二部分代表轨道高度调整量，两段基因中既有离散变量也有连续变量，因此可通过将连续变量转为离散变量的方法达到离散变量和连续变量同时参与运算的目的，如式(6)所示。

(6)

式中：Bi,hi分别代表各卫星是否参与重构变量和轨道高度调整量，Bi为0代表不参与重构，为1代表参与重构;H为轨道高度调整量上限;Bi由随机数生成函数生成[1,3)区间内的值，若Bi∈[1,2)则记为Bi=0，若Bi∈[2,3)则记为Bi=1，hi可由随机数生成函数生成分布于区间内的随机调整量值。

3.2 MOEA/D算法

基于分解的多目标进化算法(multi-objective evolutionary algorithm based on decomposition，MOEA/D)算法是Zhang等人于2007年提出的一种多目标优化算法[16]。针对多目标优化(multi-objective programming，MOP)问题，大多数应用领域均采用非占优排序遗传算法Ⅱ(non dominant sorting genetic algorithm Ⅱ，NSGA-Ⅱ)，该算法选择算子基于帕累托优于关系，复制算子迭代使用[17]，而MOEA/D算法不同于NSGA-Ⅱ算法将MOP问题作为整体对待的处理方式，为了逼近帕累托前沿，MOEA/D将问题分解为多个单目标子问题，然后同时求解这些单目标子问题[16]，进而解决整个问题。与大多数多目标优化算法相比，MOEA/D具有更快的求解速度[18]。

多目标问题可以描述为：

minK(x)=[k1(x),k2(x),…,kn(x)]

(7)

式中：x=[x1,x2,…xn]为参数向量，ki(x),i∈[1,n],为n个优化目标。采用切比雪夫分解方法可将该问题分解为多个子问题，如下式所示：

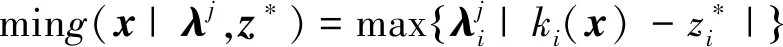
(8)

对于每个帕累托前沿上的最优解x*，存在一个权重向量λ*，使x*是式(7)、式(8)的最优解，种群规模为N时，N个均匀分布的权重向量把问题转化为了N个子问题，算法的具体流程如图2所示。

图2 MOEA/D算法流程Fig.2 MOEA/D algorithm flow

4 仿真试验

4.1 参数设置

仿真试验采用STK11与Matlab2014a互联的方式进行，其中STK负责计算覆盖重数平均值，Matlab负责算法主体并与STK互联。

试验星座为低轨Walker通信星座，地面最小观测仰角为5°，仿真时长为1 d，星座由80颗卫星组成，分为4个轨道面，相位因子为1，轨道高度为800 km，轨道倾角为60°，星座构型如图3所示。

图3 星座示意Fig.3 Constellation diagram

轨道高度调整量上限H为100 km，采用两重覆盖覆盖率来计算星座性能，假设有12颗卫星失效，失效卫星分布方式分为两种，(轨道面编号为0、1、2、3，每个轨道面内卫星编号为0至19号)，如表1所示。

表1 失效卫星分布

两种失效分布下卫星全球两重覆盖覆盖率从完整星座状态下的98.97%降低至61.86%，星座性能受损接近40%。

4.2 重构分析

算法的初始条件设置为：种群个数为70，迭代次数上限为20，交叉因子为1，变异因子为0.004，目标函数如式(9)所示。

minG=F(|Δc|,vsum,tsum,P)

(9)

式中：G为目标函数；|Δc|为当前全球两重覆盖覆盖率与失效前覆盖率差值的绝对值;vsum为重构过程星座中参与重构卫星总速度增量;tsum为参与重构卫星总消耗时间;P为用于衡量燃料消耗的均衡度，式(9)指4个指标同时最小。

(1)算例1

第一组失效分布优化结果如图4、图5所示，图中每个黑色点代表一个解，曲面由黑色点拟合而成。从图4可以看出，所有点的全球平均两重覆盖覆盖率差为零，重构总速度增量最大值为1 442.1 m/s，最小值为616 m/s，重构总时间最大值为5.35×105s，最小值为2.79×105s，燃料消耗均衡度最大值为822.2 m2/s2，最小值为261.4 m2/s2。

图4 第一组失效分布|Δc|,vsum,tsum的帕累托前沿Fig.4 Pareto front of the first failure distribution |Δc|,vsum,tsum

图5 第一组失效分布的P,vsum,tsum的帕累托前沿Fig.5 Pareto front of the first failure distribution P,vsum,tsum

(2)算例2

第二组失效分布的优化结果如图6、图7所示，从图6可以看出，所有点的全球平均两重覆盖覆盖率差为零，重构总速度增量最大值为1 188.1 m/s，最小值为579.5 m/s，重构总时间最大值为5.00×105s，最小值为2.91×105s，燃料消耗均衡度最大值为677.1 m2/s2，最小值293.4 m2/s2。

图6 第二组失效分布的|Δc|,vsum,tsum的帕累托前沿Fig.6 Pareto front of the second failure distribution |Δc|,vsum,tsum

图7 第二组失效分布的P,vsum,tsum的帕累托前沿Fig.7 Pareto front of the second failure distribution P,vsum,tsum

两组仿真试验结果表明，在两种失效分布下，轨道高度调整的办法可以使星座全球两重覆盖率恢复至失效前的水平，全部解两重覆盖覆盖率均为98.97%，考虑燃料消耗均衡性尽可能好，选取燃料均衡度最好(即速度增量方差最低)帕累托前沿上的坐标点，如表2所示。

表2 解坐标

上述仿真试验结果表明，算法有效得出了多个完全恢复星座原有覆盖覆盖率的解，构成帕累托前沿，并能挑选出燃料消耗均衡性最好的解作为星座的重构方案。

5 结论

针对低轨通信星座，提出全球覆盖率、燃料消耗均衡性、重构总时间和总速度增量四个优化指标，并采用MOEA/D多目标优化算法建模求解。仿真试验结果表明，当星座中部分卫星失效时，对不同的失效卫星分布，该方法能有效的构建帕累托前沿，恢复星座原有的覆盖性能，提供多个最优解，进而得出燃料消耗均衡性最好的几组解。但该优化过程也存在着一定的局限性，通过调整轨道高度的方式会在一定程度上破坏原有星座构型，使星座后期管理复杂度增加。在后续的研究中，可以考虑用其他的方式进行重构，并在重构过程中考虑星间链路等约束。