卫星多源信息贝叶斯融合方法研究

许迎春，赵淑敏，崇玉海，陈乃松，周倩，周涛

中国人民解放军63791部队，西昌 615000

1 引言

随着卫星技术的快速发展和应用规模的日益扩大，人们对发展费用低、性能高的先进卫星设计理念和方法提出了迫切需求[1]。在卫星的总体设计过程中，需要考虑多学科之间的紧密耦合关系，因此需要对卫星进行多学科设计优化[2]。此外，由于大量不确定性因素的存在，将导致卫星各学科之间的不确定性相互影响，不断传递，不确定性多学科设计优化应运而生[3-4]。在求解过程中，不确定性建模通过提取、描述和量化多种不确定性因素，建立不确定性分布模型[5-6]。但是，由于不确定性因素众多，如何选择合理的概率分布模型进行不确定性建模，存在较大的困难。

多源信息融合方法能将多种信息进行有效融合以获得合理的分布模型，在国内外已有较多研究。文献[7-8]提出根据专家信息融合不同分布。文献[9]采用贝叶斯理论融合卫星参数的先验信息。文献[10]采集多源寿命信息，基于D-S证据理论获得合理的融合分布。文献[11]指出信息融合的一般方法就是对所有分布加权平均。文献[12]基于确定性仿真模型，详细介绍了几何融合方法。文献[13-14]在线性融合和几何融合方法的基础上，根据KL散度衡量不同分布之间的差异以确定各个分布的权重。文献[15]基于确定性仿真模型，首次提出运用贝叶斯融合方法进行信息融合和更新。该方法在人为给定融合系数的基础上，构建了包含更多信息的参数不确定性分布模型。文献[16]根据贝叶斯融合方法，对几何融合和线性融合进一步对比。文献[17-18]在文献[15]提出的贝叶斯融合方法基础上，提出基于适应性重采样方法的迭代贝叶斯融合更新过程。文献[19]提出了一种新的基于改进重要性重采样方法的贝叶斯融合方法。但是，现有的贝叶斯融合方法及其改进方法，仅适用于两层系统结构，对于复杂的包含较多组件、分系统的多层级系统结构[20-21]很难适用。

对于多层结构的信息融合，文献[22-24]基于线性融合方法，将组件或子系统的先验知识和可靠性测试数据融合到系统层中。文献[25]设计了多机循环插入算法对多源信息融合任务调度模型进行了求解。文献[26]在系统各个层级信息已知的情况下，按照从底层至顶层的顺序对所有信息进行集成。文献[27]基于两层结构的贝叶斯融合方法，按照自下而上的方式充分融合整个卫星系统各组件、分系统的寿命信息，从而实现卫星系统的可靠性设计优化。总之，自下而上方式的信息融合方法在很多领域已有较多研究[28]。文献[29-31]将主观判断和客观数据联系起来，提出“自上而下”的信息融合方法。文献[32]构建复杂系统的贝叶斯网络结构，将底层组件层信息与顶层进行充分融合。总之，目前的多层信息融合方法是在系统层信息已知的情况下，将低层级的信息与系统层已知信息进行融合。但是，对于复杂多层系统结构，由于时间、成本的约束，很难直接获得系统层信息，并且由专家给出的系统层信息往往存在较大误差，如何充分利用低层级分布信息合理推断系统层的分布模型，是目前多源信息融合方法亟需解决的重要问题。

针对以上问题，提出针对系统层信息缺失时的卫星系统多源信息融合方法。本文的主要创新之处在于，为充分利用已知的信息，提出卫星系统多层结构模块化并基于模块化模型实现系统有效信息的合成。首先将多层系统结构划分为若干个两层结构单元，并构建多层级模块(不包含系统层)，充分利用模块中的已知节点信息。基于传统的两层结构贝叶斯融合方法，对各个模块采用从底层至顶层再至底层的融合方式，获得模块中最高层级节点的更新分布信息。基于融合更新后的节点信息，可进一步诱导得到系统节点的分布信息，使得系统节点从“无信息”至“有信息”，为进一步开展系统不确定性分析提供分布模型。

2 贝叶斯融合方法

(1)

式中：J(φ)为雅克比矩阵，J(φ)=|dθ/dφ|。当模型不可逆时，采用数值计算方法(如非参数密度估计)代替式(1)。

从上述计算过程可知，对于同一个变量φ，存在两种不同的分布来源。目前对于如何融合不同的分布来源已有较多的研究，常见的融合方法主要有两种：线性融合和几何融合[12]。线性融合和几何融合的计算公式分别为

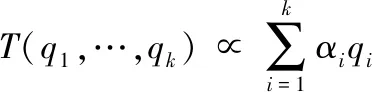
(2)

(3)

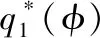
(4)

对于连续型随机变量φ，归一化常数

根据系统结构模型φ=M(θ)，系统融合分布可进一步转化为关于θ的分布，命名为子系统更新分布qθ(θ)，

(5)

综上，贝叶斯融合方法是在确定性系统结构模型和自然分布的基础上，将子系统分布信息融合至系统层，进一步将系统的分布信息传递给子系统，实现子系统和系统的分布信息更新。该方法的不足之处在于，仅适用于两层系统结构，只能实现子系统层和系统层信息的融合与更新。当系统存在多个层级时，该方法受到限制。

3 卫星系统多源信息贝叶斯融合方法

3.1 方法概述

卫星系统是典型的多层级系统，往往包含很多组件、子系统。以某卫星的双轴定位机构系统为例，如图1所示，该系统是由6个组件、2个子系统组成的3层系统结构。多层级系统的多源信息可以是连续变量的寿命信息，也可以是离散变量的不同状态概率信息等。在实际情况下，由于时间、成本的约束，很难获得系统层级的信息，如何在系统层信息缺失时充分融合低层级信息仍然是一个有待解决的问题。

图1 某卫星双轴定位机构系统Fig.1 A satellite biaxial positioning mechanism system

本文提出了一种针对系统层信息缺失问题的多源信息贝叶斯融合方法，主要包含3个部分：复杂结构的构建、结构的模块化、系统信息的合成，如图2所示。首先将实际复杂的结构用图形化的语言进行描述，构建多层次结构模型。其次通过分解和聚合的方式实现结构模块化，最后将低层级融合的信息合成至系统层级。

图2 多源信息贝叶斯融合方法的主要组成部分Fig.2 The main components of multi-source Bayesian melding method

3.2 系统结构的构建与模块化

图是目前比较常用的数据结构，可用于表示复杂的结构关系。图一般包含节点与边，两个节点之间通过有向边连接称为有向图。根据图的相关概念，将系统、各个子系统、组件以节点形式表示，节点之间的隶属关系以有向边的形式表示。因此，本文研究的多层次系统结构如图3所示。

本文将多层系统结构的各个节点、各个层级进行编号。按照升序从底层至顶层对系统各个层级进行编号，底层为最小的组件层，编号为Level 1，顶层为系统层，编号为LevelL(L≥3)。定义第i层(1≤i≤N)的第j个节点为

χi,j。根据有向图的相关定义，指向节点χi,j的第i-1层节点为χi,j的父节点，χi,j为这些父节点的子节点。对于第1层至第L-1层的所有节点，每个节点都有且仅有1个子节点。假设除系统节点χL,1外，其他所有的节点信息都存在。

在构建多层系统结构之后，对结构进行模块化处理。首先将系统结构进行分解。处于第i层的节点与第i-1层和第i+1层的节点都存在一定的关系。因此，根据节点之间的相互关系，本文将多层级系统结构划分为多个2层结构单元，如图3所示。第i层(2≤i≤N)的子节点χi,j与其在第i-1层的父节点组成一个两层结构单元，按照自下而上(Level 2→LevelL)的顺序，将整个复杂结构划分成多个两层结构单元。

图3 多层系统结构Fig.3 The multi-level system structure

本文仅考虑系统节点信息缺失的情况，进一步对分解后的系统结构进行聚合处理，如图4所示。根据L-1层节点的数目，将系统结构进一步聚合为DL-1个模块，每一个模块可看成是独立的L-1层结构。对于每一个模块，所有的节点信息都是已知的。

图4 多层系统结构的模块化Fig.4 Modularization of multi-level system structure

3.3 系统信息的“合成”

传统的贝叶斯融合方法可实现2层结构的信息融合，而划分后的每一个模块都包含若干个2层结构单元，因此，可将贝叶斯融合方法运用到2层结构单元中，实现已知信息的融合与更新。假设所有节点都是独立的，每一个模块的信息融合与更新可总结为：首先，2层结构单元从Level 1至LevelL-1进行更新，使得分布信息能从Level 1自下而上逐层传播并充分融合；在L-1层更新之后，更新过程再次通过两层结构单元自上而下进行，使得高层级的分布信息能进一步传播至低层级。以模块1为例进行说明，首先在单元1和单元2中运用贝叶斯融合方法，获得各个节点的更新分布，并将节点χ2,1和节点χ2,2的更新分布代替其自然分布；其次，基于节点χ2,1和节点χ2,2的更新分布实现单元5的信息融合与更新。以此类推，从Level 1直至更新至节点χL-1,1。再次根据更新后的节点分布，实现从LevelL-1至Level 1的更新。

当第L-1层的所有节点得到更新后，对第L-1层与第L层之间的两层结构单元进行信息融合。由于系统节点信息缺失，无法采用传统的贝叶斯融合方法实现系统节点的更新。因此，根据第L-1层的所有节点与系统节点之间的逻辑关系，基于更新后的L-1层节点信息，可得到系统诱导分布。通过上述过程得到的系统诱导分布将包含第一层至第L-1层的所有节点信息，充分利用了已知信息，使得系统节点从“无信息”至“有信息”，对进一步开展系统分析研究具有重要价值。综上，本文提出的卫星系统多源信息贝叶斯融合方法的流程如图5所示，主要步骤如下。

图5 卫星系统多源信息贝叶斯融合方法流程Fig.5 Flowchart of multi-source information Bayesian melding method for satellite system

步骤1：输入所有已知的节点信息，即Level 1至LevelL-1的节点信息。

步骤2：根据实际卫星系统，构建系统结构模型，并进行模块化处理，分解为若干个两层结构单元，并聚合成DL-1个模块，如图4所示。

步骤3：按照模块的序号进行信息融合与更新，初始化模块序号M=1。

步骤4：若M≤DL-1，执行步骤5～步骤7，否则执行步骤8。

步骤5：从Level 1至LevelL-1进行信息融合与更新，运用贝叶斯融合方法实现每一个两层结构单元的信息融合与更新，并将更新后的分布信息代替自然分布。

步骤6：从LevelL-1至Level 1进行信息融合与更新，运用贝叶斯融合方法实现每一个2层结构单元的信息融合与更新，并将更新后的分布信息代替自然分布。

步骤7：M=M+1，返回步骤4。

步骤8：根据第L-1层的所有节点与系统节点之间的逻辑关系，将更新后的L-1层节点信息进行融合。

步骤9：诱导得到系统诱导分布，使得系统节点获得低层级的信息。

步骤10：输出所有节点的更新分布并终止整个过程。

4 算例分析

4.1 问题描述

卫星姿态控制系统作为卫星系统的重要组成部分，对其进行分析研究具有重要意义。卫星姿态控制系统通常是由姿态敏感器、执行机构等构成的复杂多层系统，因此，本文选取某卫星的姿态控制系统进行研究，如图6所示。

图6 某卫星姿态控制系统组成Fig.6 Composition of a satellite attitude control system

该卫星姿态控制系统的组件、子系统的可能工作状态有4种。各个组件、子系统对应的状态及概率(自然分布)如表1所示。为方便描述，以数字0代表状态1，数字1代表状态2，数字2代表状态3，数字3代表状态4。其中，卫星姿态控制系统具有上述4种状态，但是对应的概率未知。组件、子系统、系统之间的逻辑关系可用条件概率表表示，如表2～表5所示。

表1 某卫星姿态控制系统各个组件、子系统的自然分布

表2 算例中星敏感器、红外地平仪与光学敏感器设备的条件概率表

表3 算例中光学敏感器设备、磁强计与姿态敏感器的条件概率表

表4 算例中推力器、飞轮与执行机构的条件概率表

表5 算例中姿态敏感器、执行机构与卫星姿态控制系统的条件概率表

4.2 卫星姿态控制系统建模

结合图论的相关概念，将图6所示的卫星姿态控制系统的组件、子系统等用节点形式进行描述。根据第2.2小节的系统结构构建及模块化，可将图6表示为图7。其中，χ4,1表示卫星姿态控制系统，χ3,1、χ3,2分别表示姿态敏感器、执行机构，χ2,1、χ2,2、χ2,3、χ2,4分别表示光学敏感器设备、磁强计、推力器、飞轮，χ1,1、χ1,2分别表示星敏感器、红外地平仪。由图7可知，整个卫星姿态控制系统可划分为4个单元，单元4中系统节点的信息未知。单元1和单元2组成一个3层结构的模块1，单元3同时也是2层结构的模块2，对于模块1和模块2所有节点的信息都是已知的。

图7 卫星姿态控制系统的模块化Fig.7 Modularization of the satellite attitude control system

4.3 结果分析

根据第2.3小节，首先实现模块1和模块2的信息融合，最后通过单元4的结构关系，获得系统节点的诱导分布信息。每一个模块都是基于贝叶斯融合方法，采用从Level 1至Level 3，再至Level 1的更新方式。设置每一个单元的融合系数都为0.5。在模块1中，第1层节点被更新2次，第2层节点χ2,1被更新4次，节点χ2,2被更新3次，第3层节点被更新2次。在模块2中，所有节点都被更新2次，选取节点χ2,1和χ2,3进行分析，分布变化分别如表6、表7所示(结果保留4位小数)。其中，更新次数为0表示自然分布。

表7 算例中节点χ2,3的分布变化

从表6中可以看出，节点χ2,1在更新一次之后，其分布与自然分布的差距较小，随着更新次数的增加，融合了更多节点的信息，使得更新分布不断变化，最终的更新分布与初始自然分布是完全不同的。因此，在模块1进行从第1层至第3层再至第1层的更新顺序后，各个节点信息得到了充分融合，有效利用了系统结构关系，实现了各个节点分布的更新。从表7可以看出，经过两次信息融合后，节点χ2,3的分布变化较小，但仍不同于初始自然分布，而第一次更新结果与第二次更新结果是一致的，这主要是因为模块2只包含一个2层结构单元，在进行第二次融合时，没有新的信息补充，使得最终的更新分布没有变化。总之，基于2层结构的贝叶斯融合方法，能对各个模块实现多层级信息的融合，使得各个节点包含更多其他节点的信息，低层级和高层级节点的信息得到充分融合。

进一步，根据模块1和模块2的最终更新分布，选取节点χ1,1、χ2,2、χ3,1、χ3,2的状态4概率进行分析，各节点的最终更新概率与初始自然分布的状态4概率的对比如图8所示。从图8可以看出，节点χ1,1、χ2,2状态4的更新概率与初始概率的变化较小，而节点χ3,1、χ3,2状态4的更新概率与初始概率的变化比较明显，说明在同一结构中，不同节点的更新分布变化也不相同，与节点之间的逻辑关系及节点所处的层级数有关。通过多层结构的信息融合，可获得各个节点的更新分布，为进一步系统节点诱导分布信息的获取及开展系统不确定性分析提供分布模型。

图8 算例中节点χ1,1、χ2,2、χ3,1、χ3,2状态4的更新概率与初始概率对比Fig.8 The comparison of updated and natural probabilities of state 4 for the nodeχ1,1、χ2,2、χ3,1、χ3,2

最后，由第2.3小节内容可知，在节点χ3,1、χ3,2的更新分布基础上，结合与系统节点χ4,1的关系，获得诱导系统分布，系统节点的状态与对应概率如图9所示。在系统节点信息很难获取的情况下，通过各个模块融合得到的信息，可进一步诱导推断出系统节点的信息，使得系统节点从“无信息”到“有信息”。从图9也可看出，整个系统处于不同状态的概率不同，对某些有特殊要求的系统，可进一步通过增加组件数目等方式使得系统设计满足要求。

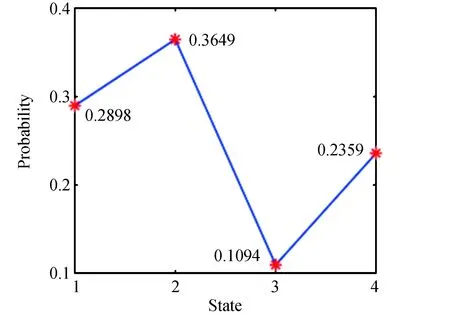
图9 算例中系统节点的状态与对应概率Fig.9 The induced distribution of the system node

综上所述，本文提出的方法能有效实现各个节点已知信息的融合，解决系统节点信息缺失的问题，基于低层级融合的信息获得系统节点的诱导分布，为设计人员提供重要参考价值，进一步有利于开展卫星系统不确定性设计优化。

5 结论

本文在传统的贝叶斯融合方法基础上，提出针对系统信息缺失的卫星系统的多源信息贝叶斯融合方法，并通过某卫星姿态控制系统算例验证了方法的可行性和有效性，主要结论如下：

1)结构的模块化处理使得复杂系统得到进一步简化，对各个模块实现多层级信息的融合，使各个节点包含更多其他节点的信息，低层级和高层级节点的信息得到充分融合。

2)算法提出采用诱导推断的方式得到系统层节点的信息，而未引入均匀分布等模糊分布作为系统节点分布，使结果更合理，更符合系统本身特性。

3)算法有效解决了系统节点信息缺失的问题，为设计人员进一步开展卫星系统不确定性分析及设计优化提供模型基础。

本文仅考虑了卫星系统的离散信息融合问题，对于连续信息融合、随时间变化分布信息融合问题还未开展深入研究，此外，采用的算例模型也较为简单。因此，本文后续工作还应探索更复杂系统结构模型和分布模型的多源信息融合问题。