视觉反馈作用下精确抓握力量控制的脑网络拓扑研究

吕亚东 李 可* 侯 莹 张冬梅 魏 娜

1(山东大学控制科学与工程学院生物医学工程研究所，济南 250061)2(南京医科大学附属苏州医院康复科，江苏 苏州 215008)3(山东大学齐鲁医院老年病科, 济南 250061) 4(山东大学苏州研究院, 江苏 苏州 215000)

引言

拇指与食指配合的精确抓握是灵巧抓取操作物体的基本手姿，也是目前运动神经科学研究的重要实验范式之一[1]。在精确抓握的运动控制中，多种模式的感知信息(包括触觉、视觉和本体感觉等)起到了关键作用。例如，不同速度的抓握力调控，就是在包括视觉信息在内的感知反馈作用下实现的[2-3]。尽管目前对精确抓握的感知运动融合已有多项研究，但对视觉反馈作用下精确抓握力-速度调制机制的研究相对缺乏。

除了分析力波动外，人们利用功能性核磁共振(functional magnetic resonance imaging, fMRI)和脑电(electroencephalography, EEG)等技术，研究了精确力控制时大脑区域的功能连通性。例如，fMRI研究发现，视觉网络(visual network)和感觉运动网络(sensorimotor network)的不同区域在产生和控制精确力方面具有不同的贡献[4]，握力幅度的增加与fMRI的响应幅度之间在初级感觉运动皮层上存在线性关系[5]。EEG研究发现，在视觉反馈作用下，所跟踪力的变化频率决定了反馈控制模式和前馈控制模式的选择。在执行正弦目标力匹配任务中，反馈控制模式主要在目标力变化频率为1 Hz以下时起主导作用，而前馈控制模式主要在目标力变化频率为2 Hz以上时占优势[6]。

与其他技术相比，EEG具有更高的时间分辨率，更便捷的采集方式，并且具有快速捕捉大脑动态结构的能力[7]。因此，EEG的采集和分析有助于揭示不同力跟踪条件下脑功能的信息。大脑的特定功能分区机制能提高信息传输的能力；不同的功能区域在力生成过程中具有不同的贡献，可以表示为具有统计依赖性的功能连接网络。大脑区域和依赖关系通常被认为是网络节点和网络边[8]。相位延迟指数(phase lag index，PLI)是常用的网络连通性的度量指标，可通过减少共同信号源的影响来获得相位同步的可靠性估计[9]。许多研究已经使用PLI来构建脑网络，并用于研究多种疾病或者认知状态下的脑活动，如工作记忆[10]、成人诵读困难[11]、精神分裂症[12]。在利用PLI构建的网络基础上，可以采用多种网络分析技术，其中图论已被证明在复杂脑网络分析中发挥着重要作用[13]。本研究使用图论，分析基于PLI构建的无向加权脑功能网络的拓扑结构。

本研究主要分析精确抓握时指力线性变化(力变化速度和上升下降状态)对大脑动态活动的影响，以便进一步深入理解精确抓握过程中的运动控制机制。本研究招募健康受试者，在力上升和下降状态下执行3种不同速度的视觉-精确抓握力量跟踪任务，然后分析基于PLI构建的脑功能网络的平均聚类系数(average clustering coefficient)C和特征路径长度(characteristic path length)L。本研究假设随着速度增加，信息传递效率增加，且力上升和下降状态存在潜在的差异性。

1 方法

1.1 实验对象

11名健康的右利手年轻人(5名女性，6名男性；平均年龄23.1岁)参与本实验。所有受试者视力或者校正视力正常，没有神经系统疾病，没有手部损伤。每个受试者在实验前进行信息采集，在知道具体要求后签署知情同意书。本实验得到山东大学审查委员会批准，并且符合赫尔辛基宣言。

1.2 实验流程

受试者采取坐姿并将其前臂放在实验桌面上，调整右手的位置以便抓握测力装置(见图1(a))。受试者先用右手拇指和食指抓握液压式手部测力计，以测量其抓握的最大自主收缩力(maximal voluntary contraction，MVC)。每位受试者共测量3次，每次持续10 s，取3次测试最大值的平均值作为其最终的握力MVC值。

在视觉-精确抓握力量跟踪实验中，受试者坐在距离计算机屏幕约62 cm处。屏幕上显示受试者实际施加力和需要跟踪的目标力[14](见图1(a))，要求受试施加的力尽可能匹配目标力。力跟踪任务包括3次试验，每次试验包括从1% MVC～10% MVC的5个周期(1个周期：上升—保持—下降—保持，见图1(b))，其中上升和下降状态称为指力线性变化。在上升和下降状态，目标力分别以1% MVC/s(速度1)、2% MVC/s(速度2)、3% MVC/s(速度3)线性增加或减小。为了避免肌肉疲劳，保持力在低范围内(10% MVC以内)变化，试验之间受试者的休息时间为3 min。在每次正式试验之前，每位受试者接受训练，以熟悉实验流程。

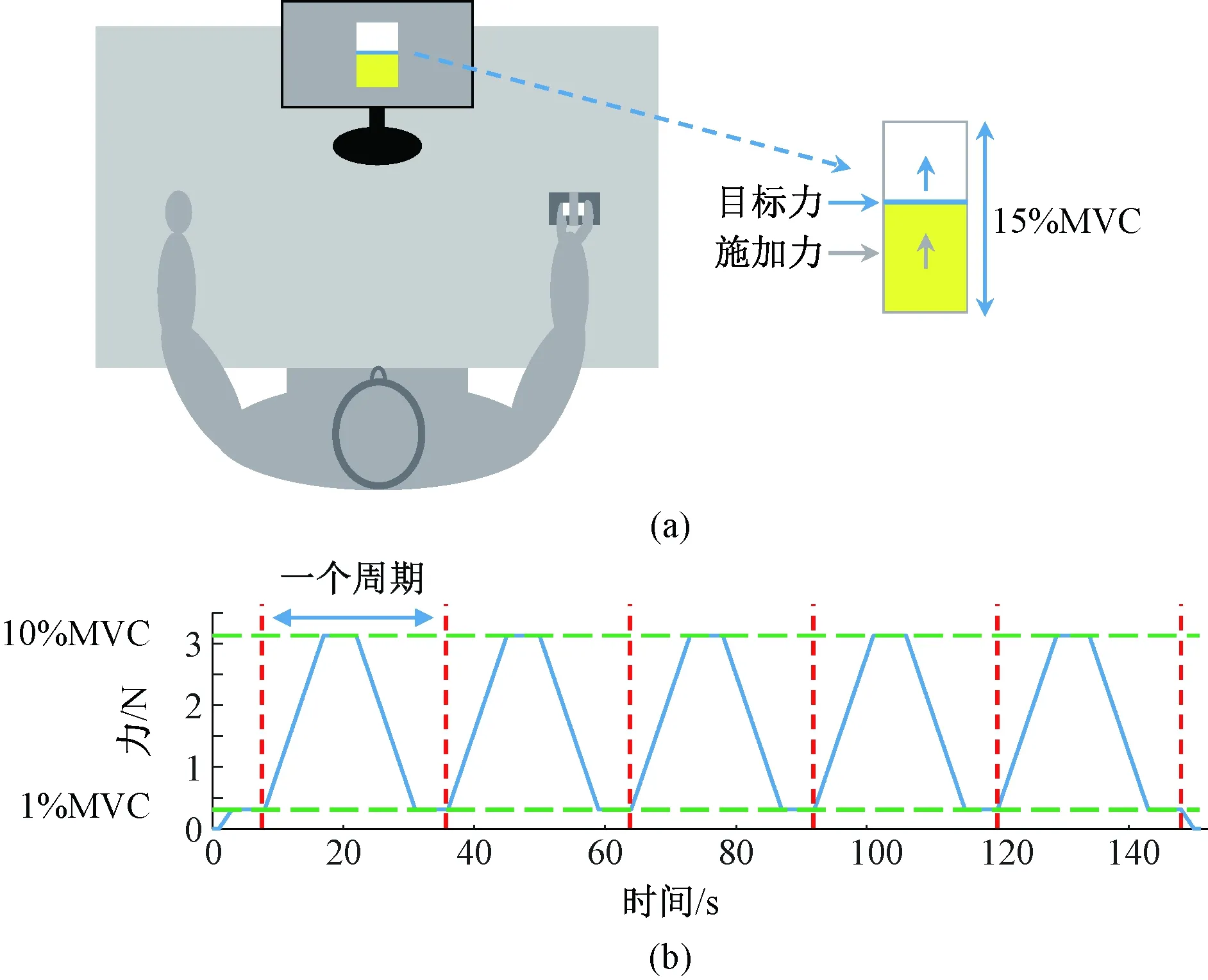
图1 实验设置。(a) 视觉-精确抓握力量跟踪任务; (b) 一次试验的目标力轨迹Fig.1 Experimental set-up. (a) Visuomotor force tracking task; (b) Target force trajectory of one trial

1.3 数据处理

本研究使用32导标准脑电帽(LIVEAMP, Brain Products Inc., Germany)，采集根据国际标准10-20系统定位的31通道EEG和放置在右眼下方的1通道垂直眼电(见图2)，采样频率为500 Hz，电极阻抗保持在5 kΩ以下。利用Brain Vision Analyzer 2.1(Brain Products Inc., LIVEAMP, Germany)，对EEG数据进行离线滤波，滤波器带宽为4～70 Hz，陷波频率为50 Hz，然后使用独立成分分析，去除眼电伪影、基线漂移和运动伪影。基于Matlab R2017b (MathWorks, Natick, MA, USA)设计有限脉冲响应滤波器，利用该滤波器从每个EEG信号中提取如下4个生理频带：θ频带(4～8 Hz),α频带(8～14 Hz),β频带(14～30 Hz),γ频带(30～70 Hz)。由于有限脉冲响应滤波器在正向和反向两个方向上处理输入信号，因此EEG信号保持原有的相位分布[15]。

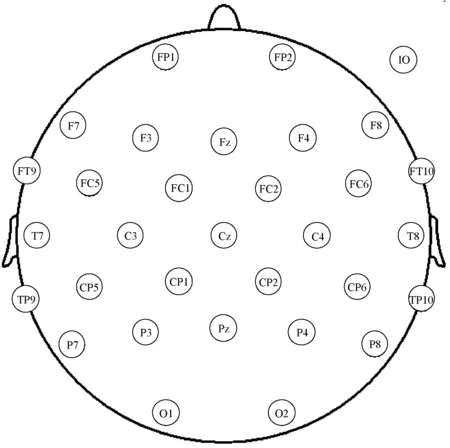
图2 32导标准脑电帽的电极位置Fig.2 32 channel standard EEG cap electrode location

1.4 数据分析

为了研究指力线性变化，本研究提取了上升和下降状态从3% MVC～8% MVC的数据，排除了从恒定力跟踪到动态力跟踪转变过程的数据。当受试者施加力和目标力之间的误差超过1.35% MVC时，该数据段被排除在接下来的分析之外。本研究使用滑窗技术，归一化在不同力变化速度下的数据段长度。每个上升或下降状态的数据段被划分成一系列的窗，窗长1 s，步长0.33 s。对于每个保留的数据段，在每个窗内构建基于PLI的脑网络，计算网络拓扑特征，然后在所有窗对网络拓扑特征取平均。在每种跟踪速度条件下，计算所有保留上升或下降状态数据段的参数，然后进行平均。

使用PLI来计算31通道EEG的所有成对连接，PLI能够捕捉相位同步性的估计，并且对共同源影响不敏感(如体积传导效应或者主动参考的影响[16])。

对于一通道EEG信号xk(t)，它的幅值Ak(t)和瞬时相位Φk(t)能够通过希尔伯特变换表达，有

(1)

瞬时相位Φk(t)可以计算如下：

(2)

在获得两通道EEG信号xk(t)和xj(t)的瞬时相位Φk(t)和Φj(t)后，计算瞬时相位差Δφkj(t)如下：

Δφkj(t)=Φk(t)-Φj(t)

(3)

作为由两通道EEG信号计算的相位差分布不对称指数，PLI计算如下：

(0≤PLI≤1)

(4)

式中，sign为符号函数，l=1,2,3，…，M表示瞬时相位差的时间序列。

PLI的范围在0～1之间。PLI=0表示两组信号之间没有耦合或者耦合的相位差为0或π倍，这种相位差很可能是由体积传导效应造成的；PLI=1表示完全同步，具有完美的非零相位锁定，这种非零相位锁定越强，PLI将越大。

使用PLI构建连接矩阵(尺寸31×31)，有许多方法可以凭经验定义脑功能网络的节点和边。在应用图论分析功能特定的大脑区域之间的统计依赖性的过程中，大脑区域和功能连接分别被定义为节点和边。本研究将31个脑电电极当作节点，将成对的多通道脑电信号之间计算的PLI值作为边，用来生成大尺度的加权脑网络。

为了比较网络拓扑特征，选择指定的阈值，以便将连接矩阵转换为邻接矩阵。阈值的选择对于网路拓扑属性的估计具有至关重要的作用，已经开发很多技术来处理阈值选择问题，如最小生成树[17]、基于显著性差异的选择[18]、替代数据分析[19]等。至今为止，对于阈值选择的最优技术还没有统一的认识，本研究采用基于显著性选择阈值的方法。在先前的研究中，使用阈值T(10%～30%)来探索潜在的网络结构，并且在其范围内脑功能网络保持小世界性质[20]。当阈值T在10%～30%范围内以1%步长滑动时，通过观察3种跟踪速度条件下网络参数的差异性来选择最优阈值。

通过计算采用最优阈值后得到的无向加权网络的拓扑性质，比较了不同力跟踪条件下脑功能网络的拓扑特征，其中基于图论分析计算了平均聚类系数C和特征路径长度L，使用脑连接工具箱[8]描述功能性脑网络的拓扑性质。

聚类系数表征一个网络集体化程度。在一个二进制网络中，一个节点的度指的是直接连接到这个节点的边的数量。如果一个节点的度为k，那么该节点的聚类系数指的是这k个节点中所有实际存在的边与最大可能存在边的比值。类似地，加权网络的节点聚类系数Ci的计算如下：

(5)

式中，PLIik表示i和k之间连接的权重。

同时，计算用来描述功能性分离的平均聚类系数C如下：

(6)

C=0，意味着网络中的所有节点都是孤立的；C=1，意味着所有节点是相互连接的。

特征路径长度L指的是在连接网络中所有节点之间距离的平均值，代表功能性整合，其在加权网络中定义为

(7)

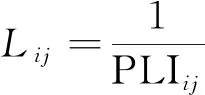
1.5 统计分析

本研究使用SPSS 25.0 (SPSS Inc., Chicago, IL)进行统计分析。在统计测试之前，使用Kolmogorov-Smirnov测试对所有参数进行正态性检验；在方差分析之前，对所有参数进行方差齐性检验。本研究采用双因素重复测量方差分析(analysis of variance，ANOVA)，对网络拓扑特征进行统计分析。使用单因素ANOVA分析来研究3种跟踪条件下网络拓扑特征的统计差异，并评估在10%～30%范围内每个阈值T的统计显着性。基于计算的参数是否满足同质性检验，使用最小显著性差异(LSD)或Tamhane′s T2进行事后比较，P<0.05被认为有统计学差异。

2 结果

本研究观察分析C、L在阈值范围为10%～30%最强连接时的变化情况，为了保持C、L值的显著性差异，在以下脑网络分析中选择最优阈值为0.26。

4个频带的脑功能连接网络的C和L如图3、4所示。总体而言，C值在θ频带的速度1～3下上升和下降时，分别为(0.157±0.032)、(0.164±0.044)、(0.194±0.039)和(0.154±0.026)、(0.173±0.041)、(0.211±0.058)，随着跟踪速度的增加而显著性增加[F=7.1，P=0.014]，同样地，C值在β频带存在类似的变化[F=11.6，P<0.001]。与C值变化不同的是，L值在θ频带的速度1～3下上升和下降时，分别为(4.644±0.400)、(4.150±0.325)、(3.909±0.497)和(4.606±0.346)、(4.040±0.471)、(3.716±0.498)，随着跟踪速度的增加而显著性减小[F=20.6，P<0.001]，并且L值在α [F=30.5，P<0.001]、β [F=136.9，P<0.001]、γ [F=45.7，P<0.001]存在与θ频带类似的变化，如图4所示。与较低速度(速度1和2)相比，最快速度(速度3)的C值在θ和β频带中的上升和下降状态显著增加，同时L值显著降低。除了在跟踪速度2条件下，β频带中L值的P=0.049之外，上升和下降状态之间没有显著差异。在3种跟踪条件下，未发现显著的相互作用。

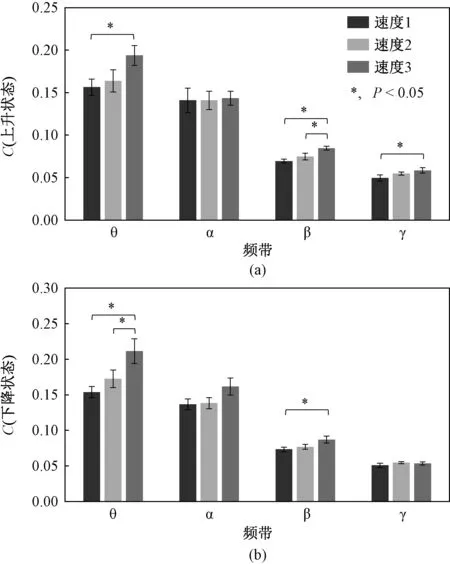
图3 脑功能网络的平均聚类系数C。(a) 和 (b) 分别为C在上升、下降状态期间的θ、α、β、γ频带，*表示3种跟踪速度条件之间的差异(P<0.05)Fig.3 Average clustering coefficient of brain functional network C. (a) and (b) represent C in θ, α, β, γ frequency bands during up-ramp state and down-ramp state, respectively. * significant difference between three tracking speeds (P<0.05)

图5显示了在不同力跟踪条件下β频带中的节点聚类系数Ci在所有受试者中的平均值。在执行上升和下降状态力跟踪任务时，聚类系数平均值随着跟踪速度的增加而增加，且主要改变发生在与执行视觉-精确抓握力量跟踪任务的感觉运动控制密切相关的中央和顶叶区域。与上升状态相比，更多的额叶区域被激活，以执行下降状态跟踪任务，这些结果反映了执行精确力跟踪任务时不同的感觉运动控制策略。使用Matlab中的EEGLAB工具箱，绘制脑电地形图[21]。

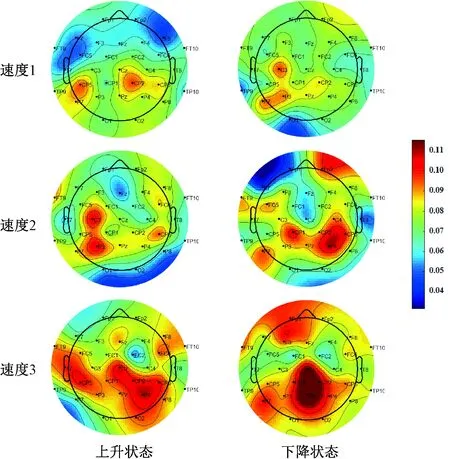
图5 不同跟踪速度和状态下β频带的节点聚类系数(使用Matlab中的EEGLAB工具箱绘制脑电地形图)Fig.5 Nodal clustering coefficient in β frequency band in different tracking speeds and states(The EEG map was drawn using the EEGLAB toolbox in Matlab)

3 讨论

笔者研究了与指力线性变化(力变化速度和上升下降状态)相关的脑功能网络动态变化，以探索精确抓握期间精细力控制的感知运动控制机制。为了研究速度和状态的影响，首先设计了视觉运动上升-保持-下降-保持力跟踪任务，然后对基于PLI构建的脑功能网络进行图论分析，探究随速度和状态变化的拓扑特征。在θ和β频带的感觉运动相关脑区，发现随着速度增加而升高的C和降低的L，这表明信息传递效率随速度改变而发生与运动控制区域相关的变化。

视觉-精确抓握力量跟踪任务是一项复杂的运动，需要神经肌肉和骨骼系统间的合作，特别是在大脑中执行多个大脑区域的协调激活，以完成精确抓握。例如，枕叶处理视觉信息输入，中心区域产生运动命令。在先前的研究中，通过在给定电极位置处EEG信号的幅度和功率改变，观察特定脑功能的激活或抑制[22]；现在使用脑网络技术，从全脑角度来研究大尺度脑区域之间的协调激活和信息流动。在健康人脑中存在两种对比特性，功能性分离指的是局部脑区域中的专门信息处理，功能性整合指的是信息传输的整合[4, 23]，平均聚类系数和特征路径长度能够很好地表征脑功能的分离和整合[24]。

随着力跟踪速度的增加，C值增加集中在θ和β频带，而L值在θ、α、β、γ频带中减小，这意味着受试者在适应更高速度的变化力时，功能性分离和整合得到增强。通过募集更多的神经资源来调节大脑活动，以提高全局和局部信息流效率，以应对更高的力跟踪速度所带来的挑战，从而导致在不同的频带振荡范围内C增加、L减小。C和L反映了不同跟踪速度下脑网络的代表性拓扑特征，对于不同的频带，推断局部信息流变化在θ和β频带变得更加明显，而全局信息流依赖于所有频带[24]。感觉运动皮层能够维持稳定的运动输出，这可以通过β频带的皮质肌肉耦合振荡来体现[25-26]。在以后的研究中，可以进一步探究在低水平力(10%MVC)控制下神经肌肉间信息流动是否存在与脑功能网络类似的频带依赖关系。

与图3、4中全脑网络的C和L值相比，发现与运动相关的中央，顶叶和颞叶脑区的激活随着速度的增加而增强。当速度变化时，没有在上升和下降状态之间发现显著性差异。如图5所示，与上升状态相比，在下降状态力跟踪时，更多的前额区域被激活，意味着更多的意识参与到力控制中[27]。

4 结论

本研究旨在探讨在执行具有不同速度和上升下降状态的视觉-精确抓握力量跟踪任务期间，健康受试者群体中的EEG动力学。通过使用网络拓扑特征C和L，将图论分析与基于PLI的脑功能网络相结合，结果显示：随着速度增加，全局和局部连接效率增强，意味着在适应速度差异期间大脑网络连接模式被改变；在下降状态力控制时，额叶中可观察到更多的局部激活，涉及更多的神经意识。通过这项研究，为探究不同力变化速度和上升下降状态下精确抓握的感知运动控制机制提供了依据，也为神经系统疾病后手功能的康复状态提供了新的评估手段。