太阳风湍流强闪烁信道下BPSK误码率闭式近似

杨露露 胡圣波，2 莫金容 蔡嘉楠

（1. 贵州师范大学智能信息处理研究所，贵阳 550001；2. 国家空间科学中心，北京 100190）

引 言

过去几十年，人类对太阳观测的散射和无线电掩星实验主要集中在S波段、X波段和Ka波段[1-4]，即将发射的太阳风-磁层相互作用全景成像卫星(solar wind magnetosphere ionosphere link explorer,SMILE)工作频段采用的也是X波段[5]. 以往的太阳观测实验表明，工作在这些频段的深空探测器发送的无线电波穿过太阳日冕时，由于受到太阳风湍流的影响，地面接收到的遥测信号会出现幅度闪烁、谱展宽和时延等现象.

事实上，当无线电波在深空中传播时，接收信号产生闪烁现象，都是由太阳日冕向外发出的充满行星际空间的等离子体流折射率的随机性引起的.从本质上看，太阳风具有湍流特性，其扰动的能谱呈现出湍流理论所描述的幂律谱形式[6-7]. 但是太阳风湍流不同于过去学术界熟悉的流体湍流，其本质仍只能通过航天器发射的无线电信号穿过太阳风，分析、反演接收信号得到[4,8]. 从这一点看，研究太阳风湍流信道对太阳观测无疑具有很重要的价值，同时有助于深空遥测系统的分析和设计.

目前，许多研究者致力于研究太阳闪烁对深空通信链路的影响. Feria等人利用太阳闪烁对X和Ka波段信号的影响观测数据，首次提出了拟合太阳闪烁指数模型[9]，为Rician信道模型下链路性能的计算提供了潜在的应用[10]. Morabito等人阐述了卡西尼号2000年在太阳上合期间的太阳闪烁效应对电波传播影响的研究[11]. 文献[12]利用非Kolmogorov模型计算了无线电波在日冕湍流中的闪烁指数，分析了日冕参数对闪烁指数和误码率性能的影响. Xu Guanju提出了基于弱日冕湍流信道下的振幅波动Gamma-Gamma分布模型，导出了自由空间光学链路误码率的解析表达式[13]. 此外，本文团队前期工作主要围绕弱太阳闪烁下的Rician信道进行了研究[14-15].

上述文献都是在弱太阳闪烁下进行信道模型研究，在强太阳闪烁条件下不具备普适性，所以难以在强太阳闪烁条件下进行信道分析. 目前国内外关于强太阳闪烁信道模型的研究很少，也没有相关的误码率性能分析. 因此，建立适应于强太阳闪烁信道模型，研究其误码率性能，有助于深空遥测系统的分析和设计.

与太阳风一样，大气也具有湍流特性. 描述大气湍流信道的统计模型主要有对数正态分布、ΓΓ分布、K分布、I-K分布等. 其中，根据大气弱湍流及强湍流条件，Trung等人分别采用对数正态模型和ΓΓ模型，研究了自由空间光多输入多输出(multipleinput multiple-output, MIMO)通信系统不同配置对平均信道容量的影响[16]；Le等人研究了ΓΓ分布大气湍流信道下自由空间光通信差错控制问题[17]；Olanrewaju等人则研究了光空间调制性能[18]；NISTAZAKIS等人分别分析了K分布、I-K大气湍流信道下自由空间光链路的中断容量[19]. 但是，在这些统计分布模型中，普遍认为对数正态分布比较适合描述弱大气湍流信道[20]1703，而从理论和实验数据一致性看，对于强湍流，K分布更适合描述大气湍流信道[21]. 当然，这些统计分布模型都考虑了大气随机介质折射率结构参数.

K分布模型建模强湍流已成功应用于大气散射和电离层闪烁[22-23]，由于电离层闪烁与太阳闪烁具有一定的相似性，所以参考电离层信道的建模有助于对太阳风湍流强闪烁信道进行建模. 本文借鉴大气湍流信道研究经验，通过分析太阳风湍流引起的遥测信号幅度闪烁特性，建立了遥测链路太阳风湍流强闪烁信道K分布模型；利用Laguerre正交多项式，完成信道K分布近似，研究参数β对分布近似KL(Kullback-Leibler)散度的影响，并给出太阳风湍流强闪烁信道下二进制相移键控(binary phase shift keying，BPSK)误码率闭式近似. 本文研究可为深空遥测系统的分析和设计提供一些理论依据.

1 太阳风引起的遥测信号幅度闪烁

1.1 U函数

当深空探测器发送的无线电波穿过太阳日冕时，受到太阳风湍流的影响，地面接收的遥测信号性能会下降，特别是在行星上合期间，当太阳-深空探测器-地球(sun-earth-probe, SEP)夹角较小时，有可能无法建立可靠的传输链路，如图1所示[14]245. 图1中R是太阳中心距L的最小距离，L=L1+L2，θ即SEP夹角.

根据Armstrong和Woo提出的理论模型，假设深空探测器发射的单色平面波信号穿过太阳风抛射的多层带电粒子，并由地球站接收[24-25]. 接收到的遥测信号出现幅度闪烁现象，这种闪烁现象可用散射理论中的U函数描述[3]7：

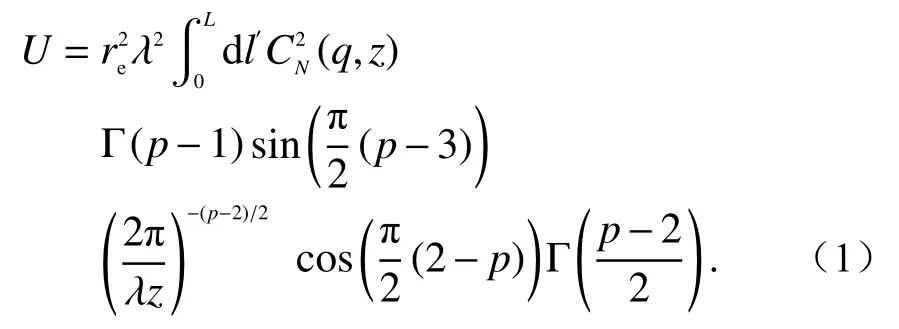
式中：re是电子半径；λ是波长；l′是沿信号传输路径从地球到积分点之间的距离；L是总信号传输距离；是带电粒子密度扰动水平；q是波数；z=(L−l′)l′/L是到屏的有效距离；Γ(·)是Gamma函数；p是折射率指数波动谱的幂律指数，对应于太阳风随机介质折射率结构参数.

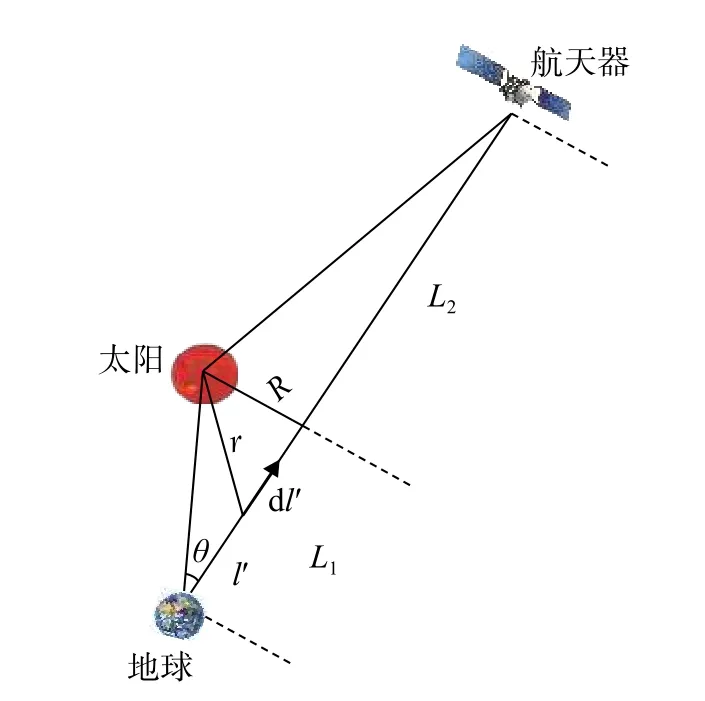
图1 上合期间无线电波穿过日冕区时的几何图Fig. 1 Geometrical diagram of radio waves passing through the corona zone during the upper closing period

式(1)散射模型中，假设带电粒子(电子密度)不规则性的三维空间谱是各向同性的，并具有如下形式[3]7：

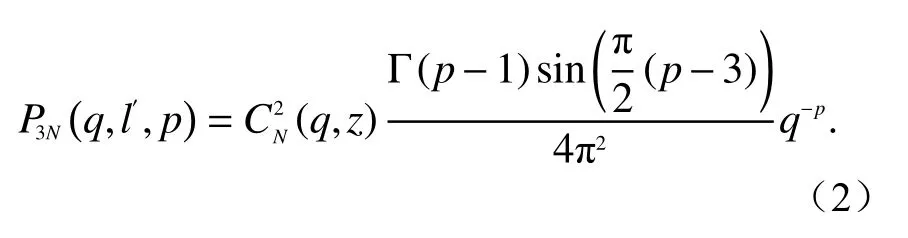
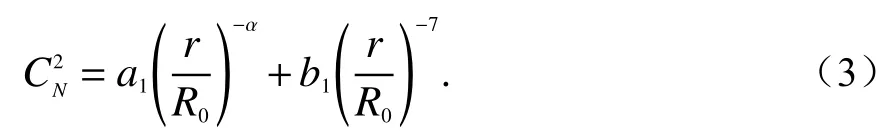
式中：r是太阳到信号路径积分点的距离；R0是太阳半径.

类似于Kolmogorov湍流，其单位为m−6.67[1]4.

1.2 闪烁指数

信号幅度闪烁程度可用闪烁指数m描述. 闪烁指数m可从观测到的遥测时间信号计算得到，并可定义为接收信号强度起伏的均方根值与接收信号强度均值之比，即如记接收信号强度起伏为If=I−〈I〉，则[26]

式中，I是接收信号强度. 而m与U函数的关系为[3]7

根据不同的U值，受太阳风湍流影响，遥测信号幅度闪烁可分为三类：①U≪1，m≪1时，对应于弱闪烁；②m→1，对应于饱和区；③m>1，对应于强闪烁. 从1.1节分析可见，影响闪烁强度大小的因素很多，其中最主要的因素是太阳与遥测链路的距离和频率. 例如，当SEP角减小时，闪烁指数会增加直到饱和，即使SEP角进一步减小，m值也不再增加. 对于X频段(8.4 GHz)，当SEP角为0.6°左右时，即进入饱和区，而对于Ka频段(32 GHz)，当SEP角为1.1°左右时，即进入饱和区[3]2.

此外，在某些情况下，给定一个SEP角，如果已知一个频段的闪烁指数，则可估计另一个频段的闪烁指数，由于[1]5

因此，如果X和Ka频段的闪烁指数分别为mX和mKa， 则有

由式(8)知，对于Kolmogorov湍流，p=11/3，mKa/mX约为0.15.

2 遥测链路太阳风湍流强闪烁信道模型

长期以来，太阳风湍流特性，不管是湍流强度，电子密度起伏，还是太阳风速度，一直都是研究热点.究其原因还是对太阳风知之甚少，而多是依靠少量探测数据进行研究[27]，如太阳风湍流的数值仿真. 太阳风湍流的数值仿真主要依据太阳风磁流体动力学机理(magneto-hydrodynamic, MHD)和太阳观测数据，Goldstein等人采用阿尔芬脉动的串级理论[28]、Franci等人应用混合编码电流超前法(current advance method et cycLIc leApfrog, CAMELIA)演算法完成了太阳风湍流的三维仿真[29]，Robert等人则根据太阳风湍流空间谱和热力学演进原理开展了2.5维的太阳风湍流数值仿真[30]. 综上可知，遥测链路太阳风湍流信道模型的建立可依据有关理论和太阳观测数据.

2.1 太阳风湍流强闪烁信道的K分布模型

以BPSK为例，对于深空探测遥测系统，接收到的信号可表示为

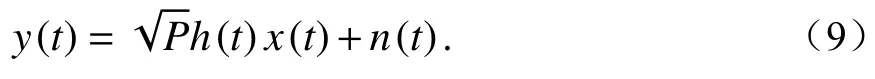
式中：P是遥测系统发射机功率；h(t)是太阳风湍流引起的信道闪烁(衰落)增益；x(t)∈{−1,+1}是发射的信号；是0均值加性高斯白噪声. 当h(t)的概率密度函数为K分布时，太阳风湍流信道即为K分布信道，此时h(t)的概率密度函数表达式为[31]5

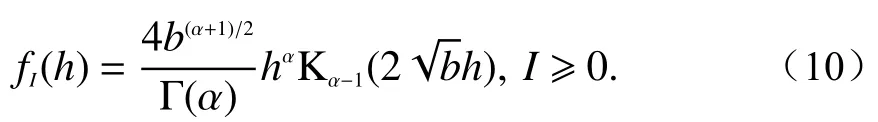
式中：Kn(·)是第二类修正贝塞尔函数；b=α/µ，其中µ是平均强度，α是太阳风湍流K分布信道参数，与闪烁指数m的关系为[32]

式(10)各阶原点矩为[20]1704

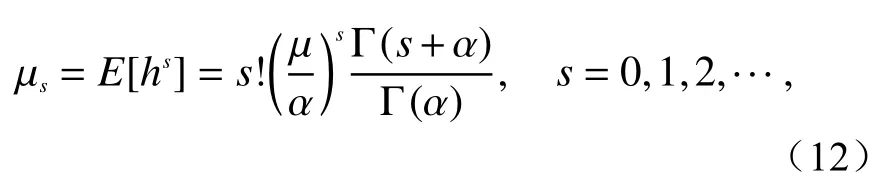
且各阶矩的递推关系为

其中，E[h0]=1.

2.2 闪烁指数观测与SEP角的数值拟合

由式(11)可知，闪烁指数反映遥测信号闪烁程度，是决定遥测链路太阳风湍流信道模型的重要参数. 由1.2节又可知，闪烁指数与SEP角密切相关，依据Cassini航天器观测数据，选择多项式/指数组合模型拟合的SEP角与闪烁指数关系如图2所示[1-2].

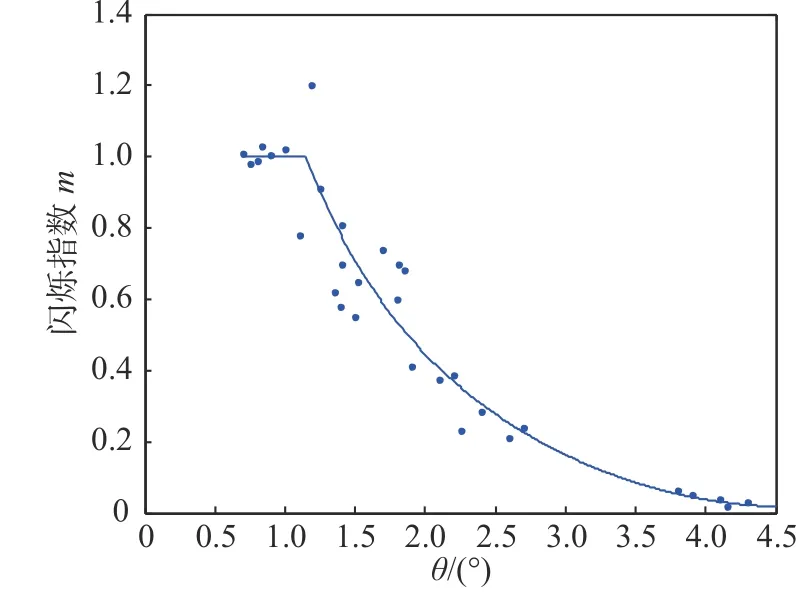
图2 闪烁指数观测与SEP角函数关系拟合曲线Fig. 2 scintillation index observations as a function of SEP angle function

从图2可见，当θ<θt时，进入强闪烁区(m>1)，且其取值在1附近[2]8. θt是弱闪烁(m<1)到强闪烁区过渡点的SEP角.

3 太阳风湍流强闪烁信道的K分布模型和误码闭式近似

误码率是衡量遥测链路可靠性的重要指标之一.在K分布信道条件下，Kiasaleh和Sandalidis针对遥测系统误码率已做了许多工作[23]，但给出的解析式中由于涉及复杂的Whittaker函数和Meijier函数，很难进一步分析重要参数对误码率的影响. 因此，Samimi和Azmi开展了K分布的近似研究[33]. 这些工作中，普遍采用有限个矩函数近似分布函数，这种方法对近似效果影响较大. 为此，本文利用Laguerre正交多项式方法近似K分布.

3.1 太阳风湍流强闪烁信道的K分布模型近似

假设β是任意正数，Ln(x)是拉格朗日函数，记w(βh)=βe−βh，则I的K分布可近似为[31]5

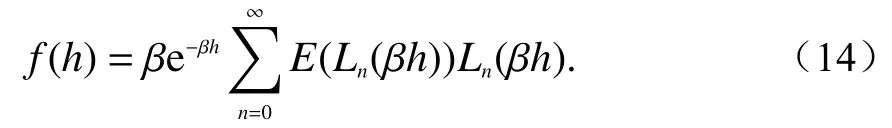
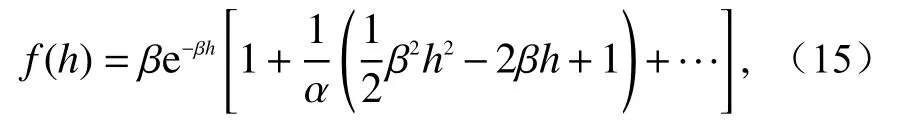
括号中取前两项，则

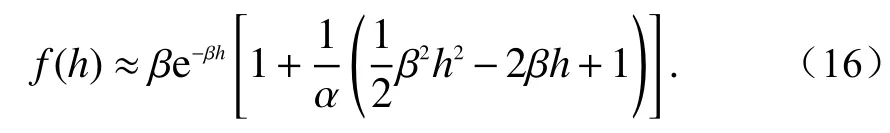
3.2 近似分布有效性分析

KL散度常用于衡量分布之间的差异程度，又称为相对熵、信息增益[34]. 为便于分析近似分布的有效性，本文使用KL散度来度量Laguerre正交多项式与K分布的近似程度.

给定两个概率分布pX(x)与qX(x)，它们的KL散度为[20]1704

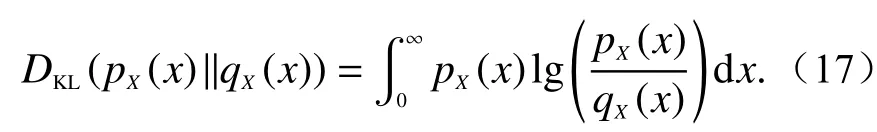
式中：pX(x)为精确分布；qX(x)为近似分布. 当KL散度越小时，则两个分布越相似；反之，则两个分布差别越大.

图3给出了K分布的平均强度µ=1时，随着β值的变化，Laguerre正交多项式与K分布的KL散度变化.

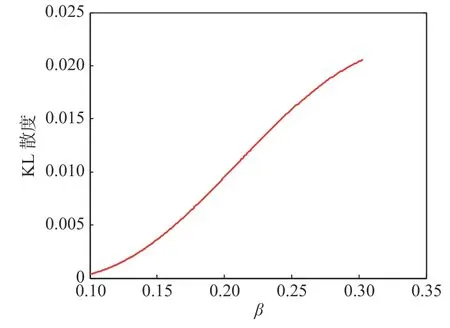
图3 Laguerre正交多项式与K分布之间的KL散度随β值的变化Fig. 3 KL divergence between Laguerre orthogonal polynomials with different β values and K distribution

从图3可见，随着β增大，近似分布与K分布之间的KL散度也越来越大，这也可从表1所列KL散度值得到证实. 因此，可选择较小的β，使KL散度较小，以得到Laguerre正交多项式近似分布.

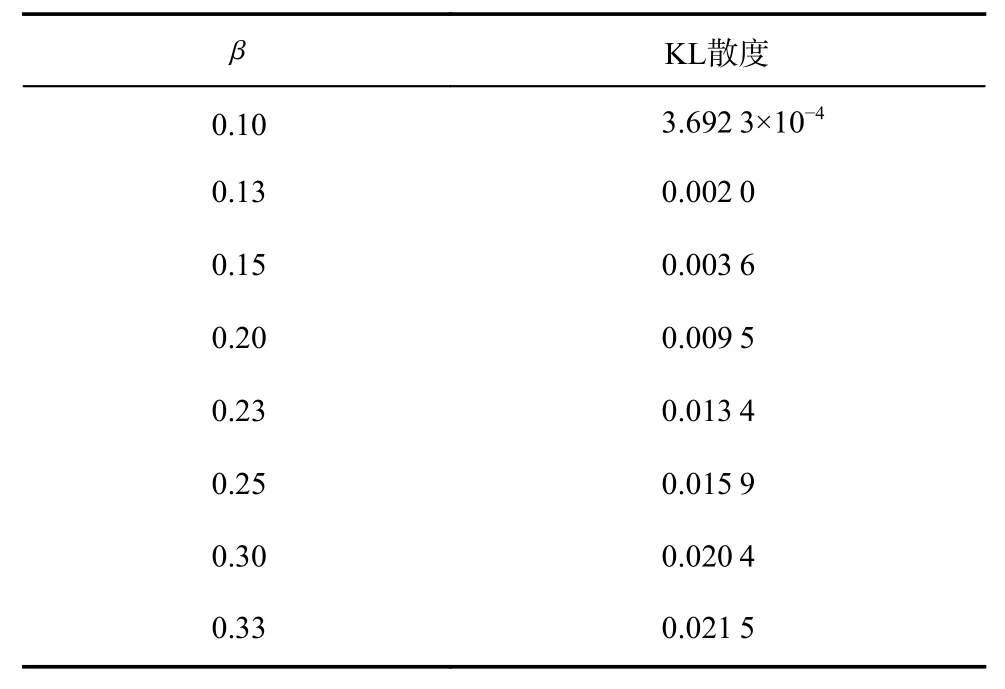
表1 Laguerre正交多项式与K分布的KL散度值Tab. 1 KL divergence values of Laguerre orthogonal polynomial and K distribution

3.3 误码率的闭式近似

一般地，对于相干BPSK解调，高斯白噪声信道下误码率可表示为

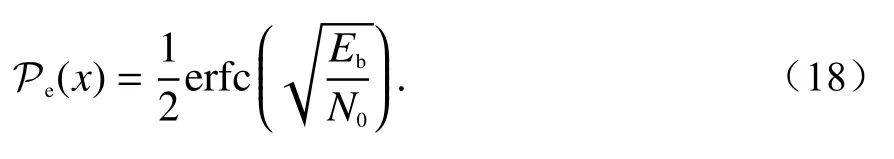
式中：Eb/N0为余接收信噪比；erfc(·)为余误差函数.则太阳风湍流信道误码率可表示为[35]

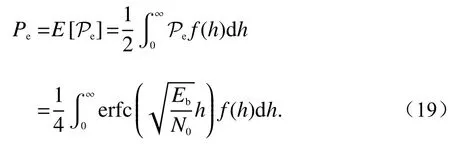
根据误差函数积分[36]，结合式(16)，记γ，式(19)可近似为

对式(20)化简可得

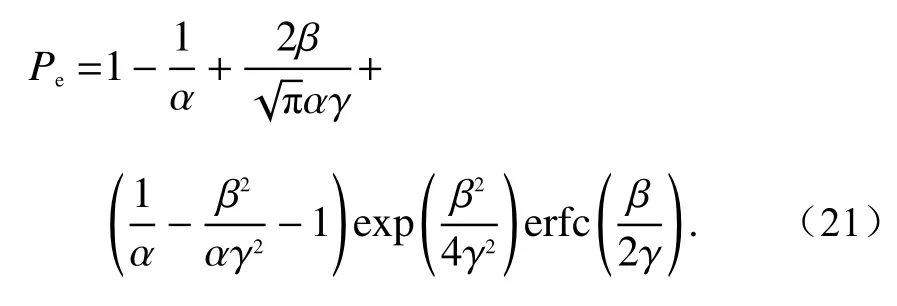
根据式(21)，图4给出了在不同信噪比下误码率函数Pe关于β的一阶导函数曲线. 从图可见，当β在0到5范围内时，不同信噪比下一阶导均大于0，说明误码率Pe是关于β的一个增函数.根据式(21)，又可得到太阳风湍流强闪烁信道BPSK调制信噪比与误码率之间关系，如图5所示.同时，为便于分析比较，图5还给出了无湍流时BPSK调制信噪比与误码率之间关系.

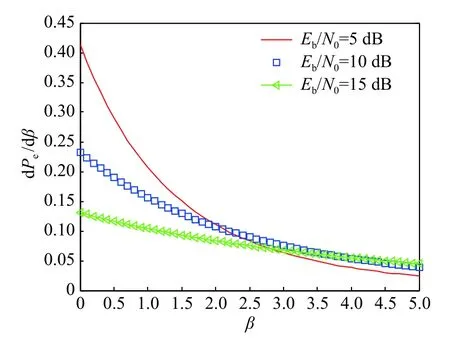
图4 误码率函数Pe关于β的一阶导函数Fig. 4 First derivative function of bit error rate function Pe with respect to β

图5 不同湍流条件下的误码率Fig. 5 Bit error rate under different turbulent conditions

结合前述，从图5可看出，太阳风湍流强闪烁对误码率影响非常明显，特别是信噪比较低时，即使是闪烁指数较小时，误码率也比无湍流时高出1～2个数量级. 从图5还可见，随着闪烁指数m减小，因湍流效应变弱，误码率得到降低. 同时，比较图5(a)和图5(b)可见，b值大时，误码率较高，这是因为b值增大，β增大，导致误码率增高.

不同信噪比下，图6给出了β值对误码率的影响结果. 由图6可以看出，信噪比相同时，随着β值的增大，误码率增高；反之亦然. 例如，当Eb/N0为5 dB时，β为0.3，误码率为0.111 3；β为0.8，误码率为0.320 4. 而当Eb/N0为10 dB时，β为0.3，误码率为0.065 5；β为0.8，误码率为0.209 4.

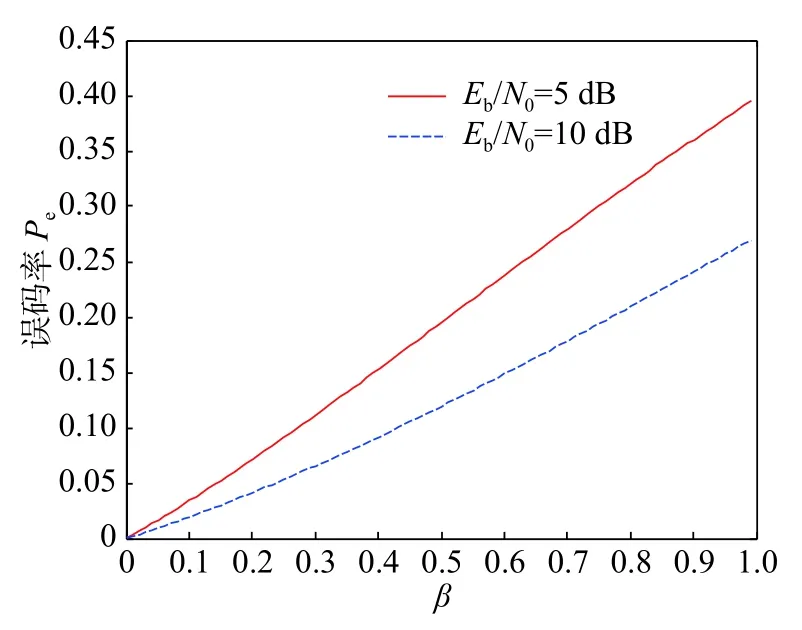
图6 不同β值的误码率Fig. 6 Bit error rate of different β values

4 结 论

在前期弱太阳闪烁信道研究工作基础上，通过建立遥测链路太阳风湍流强闪烁信道K分布模型和利用Laguerre正交多项式近似，研究了Laguerre多项式拟合参数β对分布近似KL散度的影响，给出分析了不同闪烁指数和参数β对误码率的影响，为分析和设计湍流信道下，特别是强闪烁下深空遥测系统提供了重要理论依据. 同时，通过以上工作，可得到如下结论：

1)参数β影响太阳风湍流强闪烁信道K分布近太阳风湍流强闪烁信道下BPSK误码率闭式近似，似和误码率，选择较小的值有利于降低K分布近似的KL散度和误码率，能够获得更好的信道近似，更有利于遥测链路太阳风湍流强闪烁信道的分析.

2)由于K分布在满足弱闪烁条件下可转化为Rician分布，因此，K分布的建立是合理有效的.