基于全波法的甚低频波对低电离层扰动分析

孙佳欣 彭怀云 李清亮

（中国电波传播研究所 电波环境特性及模化技术重点实验室，青岛 266107）

引 言

低电离层(60～120 km高度)是甚低频(very low frequency, VLF)电磁波地-电离层波导传播模型的上边界[1]，其电子浓度、电子温度、碰撞频率等参量的分布、扰动变化是影响VLF远距离通信效能、导航定位精度的重要因素[2]. 因此，低电离层参量的分布和扰动特性研究是VLF电波传播研究的重要方向之一.

1990年，Inan[3]分析了南极Palmer站接收的NAA台VLF传播数据，发现该VLF信号幅度被NAU台发射的VLF信号调制，实验证实了VLF波能显著改变低电离层电子温度和浓度的理论预言.Inan等人[4]、Rodriguez等人[5]分析了NSS、NAU、NAA三个VLF台发射的强VLF电磁波对夜间低电离层电子温度和电子密度的影响，发现在70～90 km高度电子温度升高2.5倍，电子密度下降26%. 1997年，刘立波等人[6]在Rodriguez的基础上，分析了电离层中氧气、氮气密度等背景参量对电子温度、浓度扰动的影响，发现中性大气数密度越低或温度越高，电子参数变化越大. 2007年，Peter等人[7]分析了闪电激发的VLF电波对电子密度的扰动，发现85 km处D层电子密度提高了约15%. 2013年，Graf等人[8]计算了VLF波引起的低电离层扰动范围和跨低电离层衰减的估计值. 2017年，冯阳[9]推导了全波分析法下的VLF波传播模型，并对不同辐射源参数、地磁场参数、电离层参数下的VLF波传输特性进行了分析.但他研究的重点是电离层中的VLF波传播情况，并没有对VLF波引起的电离层扰动情况进行分析.2018年，ATICI等人[10]利用Glukhov-Pasko-Inan电离层化学经验模型计算了雷电激发的VLF电磁波对低电离层电子密度的影响，发现由于负离子与氧、氮原子的反应，在场强为10 V/m的情况下，低电离层电子浓度提高了5.5倍，与无线电波对电离层的扰动相比，雷电引起的电子浓度扰动幅度更大. 同年，成琦等人[11]在电离层自恰加热模型的基础上，引入电子复合和吸附效应，对高频电波引起的电离层扰动进行仿真. 成琦使用的电离层化学反应模型和扰动模型与本文相似，不同之处在于，本文使用的是VLF波扰动电离层. 由于低电离层电子浓度、碰撞频率参数的高度分布在一个波长范围内剧烈变化，还需考虑各层反射、透射波的相互叠加情况.

本文首先通过全波解反射系数和波模振幅递归算法，引入不同入射角的平面波，分析了各层中上行和下行波的能量密度分布规律. 然后基于Glukhov-Pasko-Inan低电离层化学反应模型，利用梯度下降法[12]，分析了不同入射角平面波对电子温度、浓度改变的影响规律. 本研究可为细致分析偶极子源(例如VLF台、雷电)辐射的不同入射角VLF波对低电离层扰动的贡献以及扰动现象的分析、认识提供思路.

1 计算方法

1.1 平面波入射的全波法

建立电离层水平分层均匀模型，x为正北方向，y为正东方向，z为垂直向上方向. 从地面至电离层上边界(700 km)，按高度分为N层，每层的边界为zi(i=0,1,2,···,N)，z0代表地面，zN为电离层上边界.由于VLF电波频率远高于离子回旋频率，离子影响可忽略. 电离层相对磁导率为1，时谐因子为 e−jωt.θ为入射角，为波矢量与x方向夹角.l、m、n为地磁场与x、y、z轴夹角的余弦，l=cosφBcosθB,m=sinφBcosθB,n=sinθB, θB为 磁倾角，φB为地磁场水平分量与正北方向夹角.

电离层中每层的电极化率矩阵由该层电子浓度、碰撞频率决定，每层中电极化率矩阵[13]表示为

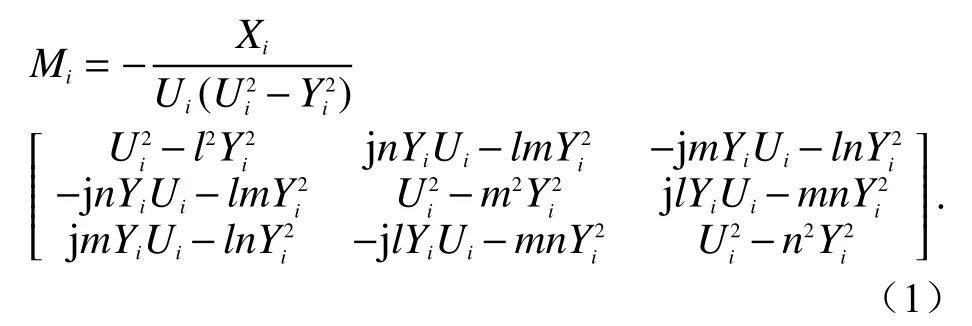
全波法将各分层中水平电场、磁场进行二维空间域傅里叶变换，并代入Maxwell方程，消去和，可得无源层中水平电、磁场的矩阵形式：

式中：

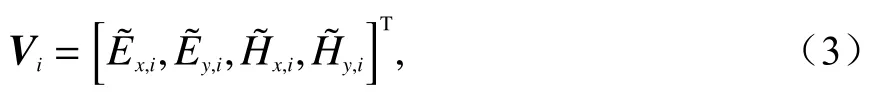
基于各层分界面水平电、磁场连续的边界条件，利用反射系数递归算法，可获得各分层界面对上行、下行波的反射系数矩阵当第0层(为空气层)中入射波为TM平面波时入射磁场为水平方向，且垂直于入射面，其二维空间域傅里叶变换表示为

式中：a为 磁场幅度，单位为A/m. 入射波的波模振幅表示为

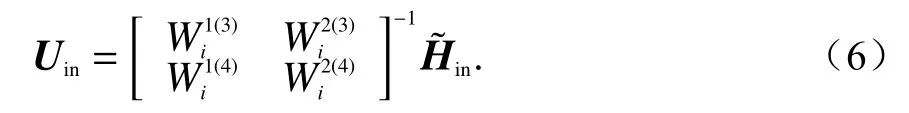
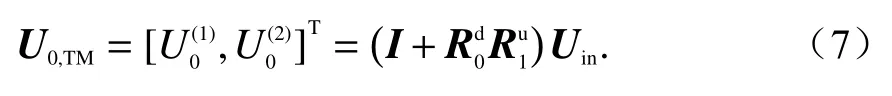
同理，当入射波为TE波时入射电场为水平方向，且垂直于入射面，其二维空间域傅里叶变换表示为

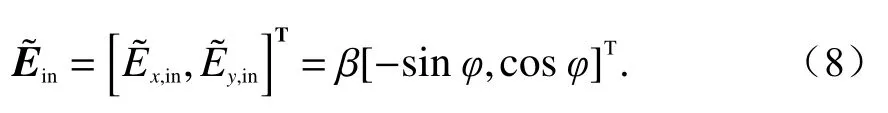
式中，β为电场幅度，单位为V/m. 对应的上行波模振幅为

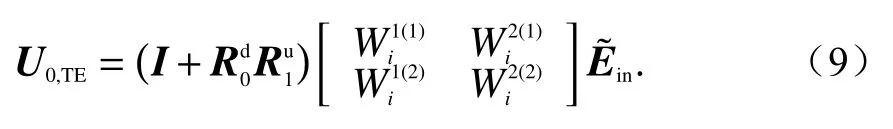
在上述平面波引入的基础上，利用波模振幅递归算法[14]，获取各层中的上行、下行波模振幅. 再依据式(4)、Maxwell方程和傅里叶逆变换计算各层中的上下行4个波模的电场和磁场. 进而基于坡印廷定理计算出各波模的平均能流密度

1.2 低电离层参数扰动的梯度下降法

在低电离层中VLF电波能量主要被电子吸收，其他粒子的吸收可忽略[15]，电离层各分层中单位时间、单位体积内吸收的能量

是4种波模吸收能量之和，单位为W/(m3·s−1)；(m=1, 2, 3, 4)为4种波模的吸收指数，

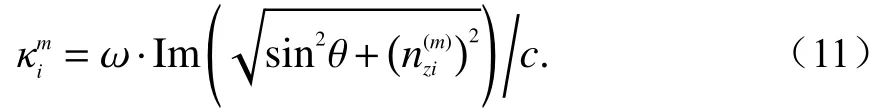
式中：c为光速；Im(·)表示取虚部.

各分层中电子温度变化由电子能量方程确定：

式中：k为玻尔兹曼常数；Li为各层电子能量损失项.

能量损失主要来源于电子与其他粒子的碰撞、中性粒子的能级激发等，其计算模型为Stubbe[16]能量损失模型.

通过式(12)可以得到电子温度随时间变化速率dTe/dt，选取时间步长Δt，用差分法将电子温度的变化过程离散化，相邻两时刻电子温度之间关系可表示为

式中：Te0为前一时刻的电子温度；Te为当前时刻电子温度. 电子温度的变化改变了电离层中电子与其他带电粒子的化学反应过程，使其浓度发生变化. 各粒子的浓度变化速率可通过Glukhov-Pasko -Inan低电离层化学反应模型[17]表达：

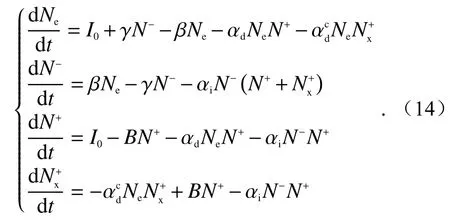
式中：Ne、N−、N+、Nx+分别表示电子、负离子、正离子、团簇离子的浓度；I0是电离层自然状态下的电子产生率，白天太阳是主要的电离源，在夜间主要由月亮反射的太阳光、人工源、其他自然因素或宇宙背景下的电离源产生；γ是电子从负离子上的脱离率；β是电子附着到中性粒子的效率；αd是电子与正离子复合系数；是电子与团簇粒子的结合率；αi是负离子与正离子和水合正离子之间的复合系数；B是初级正离子转化为水和离子的转化率. 电子温度的扰动改变了带电粒子间的反应系数，进而对各粒子成分浓度造成影响. 与式(13)同理，相邻两时刻的各粒子浓度关系可表示为

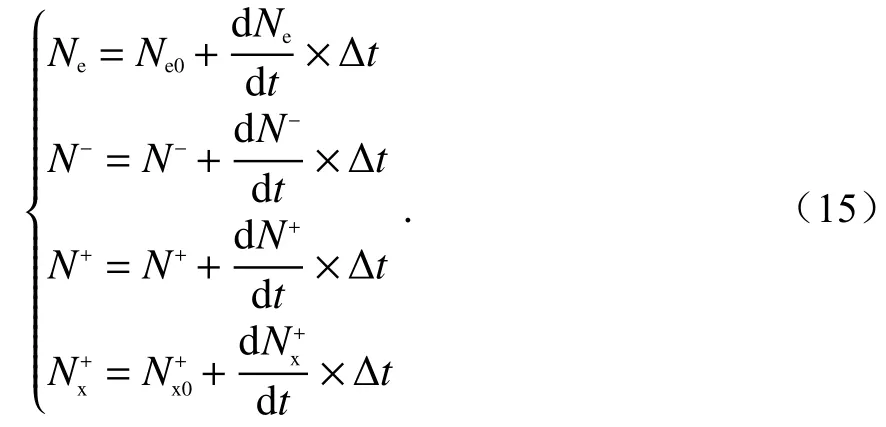
将初始电子温度、浓度等参量带入式(1)～(11)，用全波法计算电波能流分布、低电离层能量吸收，进而得到时间步长Δt后的电子温度、电子和离子浓度. 如此循环迭代，直到电子温度和带电粒子浓度不再发生变化，即可实现VLF电磁波对低电离层扰动的计算仿真.

为加快迭代模型的收敛速度，Δt的选择采取梯度下降法，将电子浓度的变化率作为损失函数，使Δt随电子浓度变化率改变：

式中，ζ为学习率，取ζ=1×10−9.

2 计算分析与讨论

2.1 扰动结果对比

文中使用的电离层中性大气参数来源于MSISE-90模型. 正离子密度、电子温度、80 km高度以上的电子数密度来源于IRI-2016或文献[4]中使用过的经验模型. 在无特殊说明的情况下，平面波入射方向为垂直向上，即θ=0°、φ=0°，地磁场方向为θB=60°、φB= 0°，大小为50µT. 入射波频率设置为f= 10 kHz，输入能流为8×10−6J/(m3·s−1).

在上述条件下，分别用Rodriguez[18]方法和本文方法对电离层扰动情况进行仿真. 图1(a)、(b)分别给出了全波法得到的电场、磁场分量二维仿真图. 由于本节引入的是TM平面波垂直入射电离层，电场、磁场垂直分量很小. 随着透入电离层的高度增加，电波方向发生改变，80 km以上高度出现了电场z分量.图2为两种方法得到的电离层能量吸收随高度的变化. 在85 km以下高度，能量吸收差别很小；85 km以上区域，两种方法得到的能流吸收峰值都在90 km高度附近. 不同的是，由于全波法考虑到电离层各分层中反射、透射波相互叠加的情况，在进入电离层能流相同的情况下，电离层能流吸收要大于Rodriguez方法得到的能流吸收.

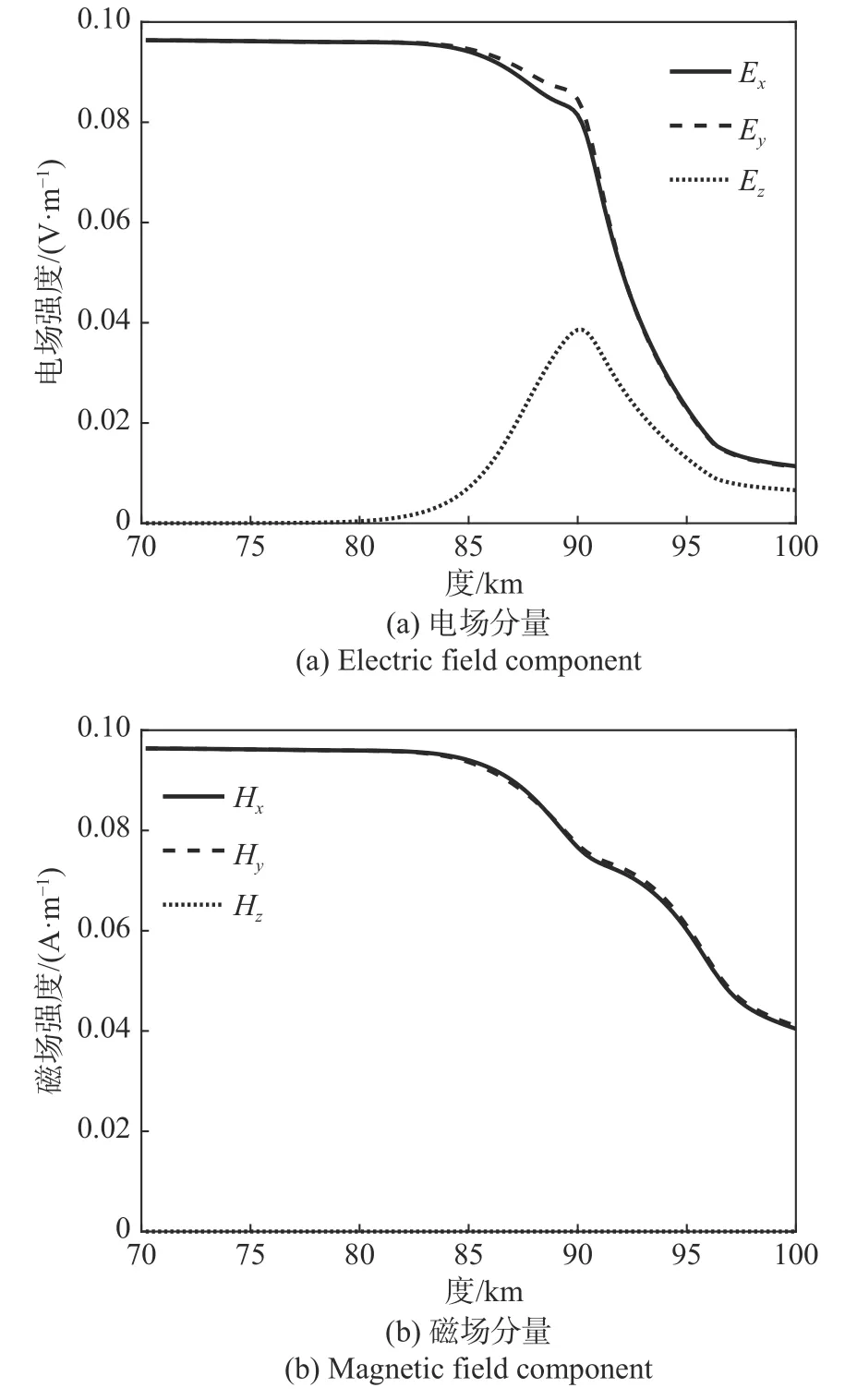
图1 电磁场分量随高度的变化Fig. 1 Variation of electric field and magnetic field component with height

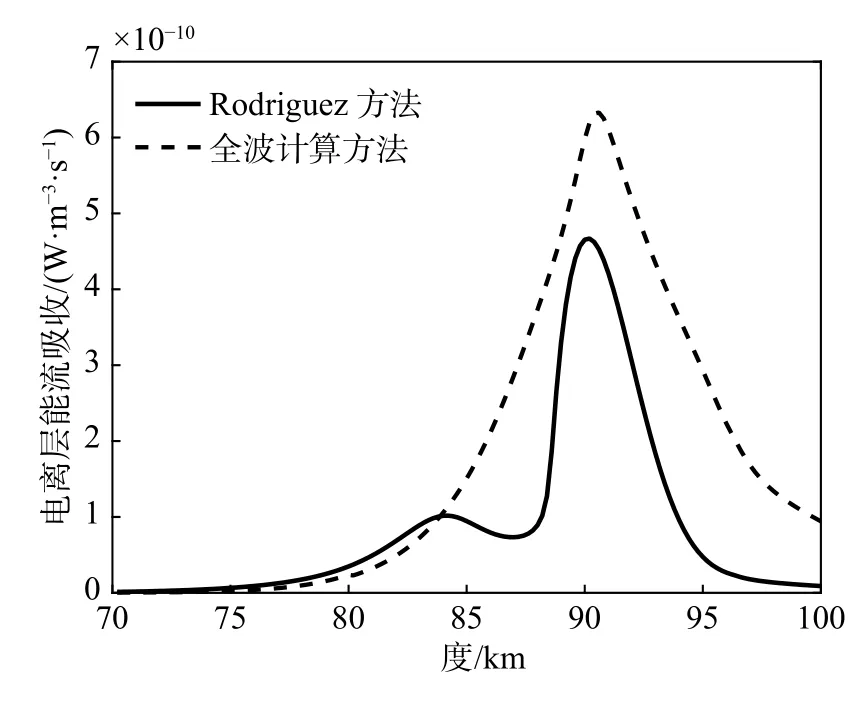
图2 电离层能流吸收对比Fig. 2 Comparison of energy flow absorption in the ionosphere

图3给出了Rodriguez方法和全波计算方法得到的电子温度扰动对比. 与图2中的能流吸收情况相对应，Rodriguez方法中电子温度的变化主要集中在70～95 km高度范围内，电子温度在85 km和90 km高度附近存在两个峰值点，最高可以达到290 K. 用全波法得到的仿真结果中由于电离层能流吸收集中在90 km高度附近，电子温度的扰动范围主要集中在75～100 km且仅在90 km处有一个峰值点，最高可达320 K. 可以看出，波模的反射迭加不仅提高了电离层的能流吸收，电子温度扰动幅度也随之增大.

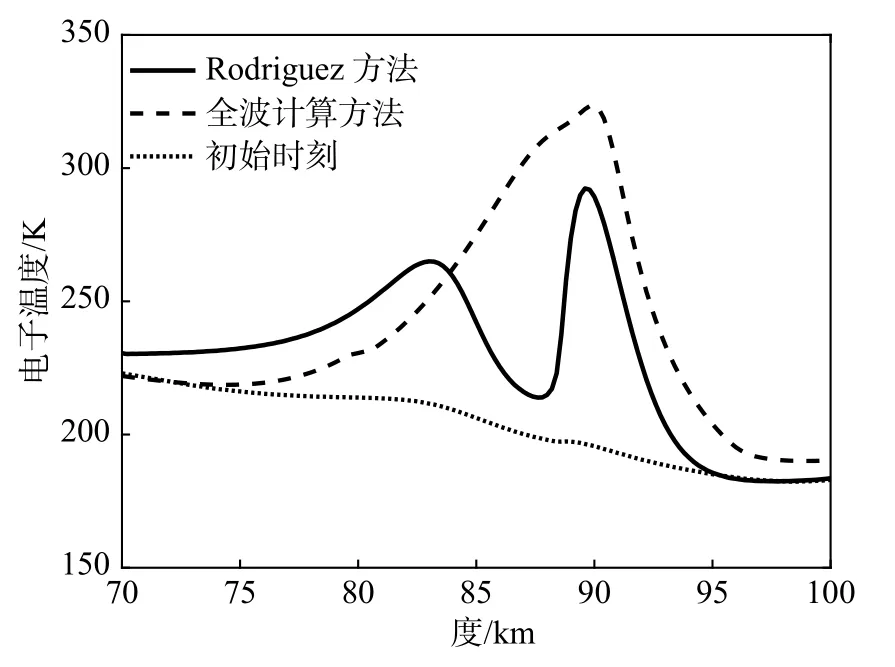
图3 电子温度扰动对比Fig. 3 Comparison of electronic temperature disturbance

电子温度的扰动导致电子浓度发生变化，图4给出了电子浓度与初始时刻的比值，受背景电子浓度分布的影响，扰动的幅度和高度与电子温度存在一定差异. Rodriguez方法仿真的结果中，电子浓度在83 km处损耗最大，降低了约12%. 用全波法得到的电子浓度模型中，电子在85 km损耗最大，由于85 km处的背景电子浓度较高，浓度损失反而不如Rodriguez方法的结果明显，降低了约10%. 在93 km以上区域，由于电子温度的提高降低了电子与正离子的复合效率，该区域内的电子浓度反而有所提高.

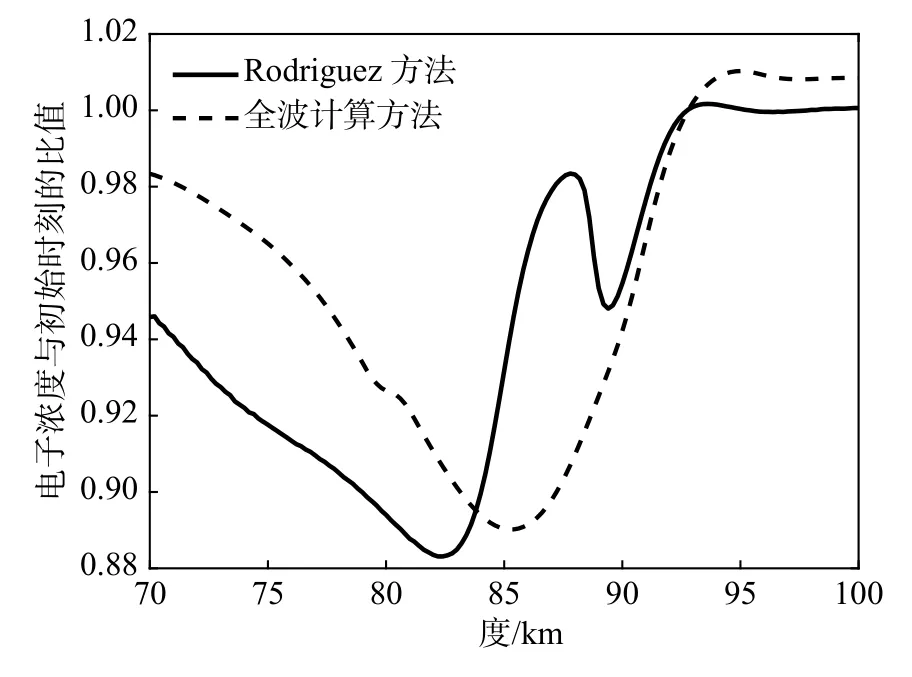
图4 电子浓度扰动对比Fig. 4 Comparison of electron concentration disturbance

2.2 不同入射波、地磁场条件下的扰动结果对比

2.2.1 入射角变化对电离层扰动的影响

将磁倾角设为60°，地磁场水平分量指向正北方向，在入射波水平方向的分量与正北方向夹角φ为180°的情况下，本节对比了入射角 θ对电离层扰动的影响. 图5(a)、(b)分别给出了各高度下电场、磁场矢量随入射角的变化，可以看出，电场的衰减主要发生在90 km以上高度，磁场的衰减主要发生在85 km以上高度. 图5(c)为不同入射角下的电波能流对比，可以看出，90 km高度以下区域，入射角θ = 30°的情况下电波能流密度最大，反射透射波的叠加使80～90 km高度范围内的能流密度大于入射波能流密度.90 km高度以上区域，入射角θ=0°时，能流密度最大，这是因为VLF波垂直入射电离层时穿透性最强，能流密度随高度衰减最慢.

图6给出了不同入射角对应的电离层能流吸收情况，电离层能流吸收主要集中在80 km以上区域，随着入射角增大，能流吸收峰值所在高度逐渐从92 km向85 km偏移，由于电波在反射面附近能流吸收最大，进一步证明了改变入射角会影响电波的反射、吸收高度. 入射角越大的情况下，电波穿透性越弱，反射吸收面高度越低.

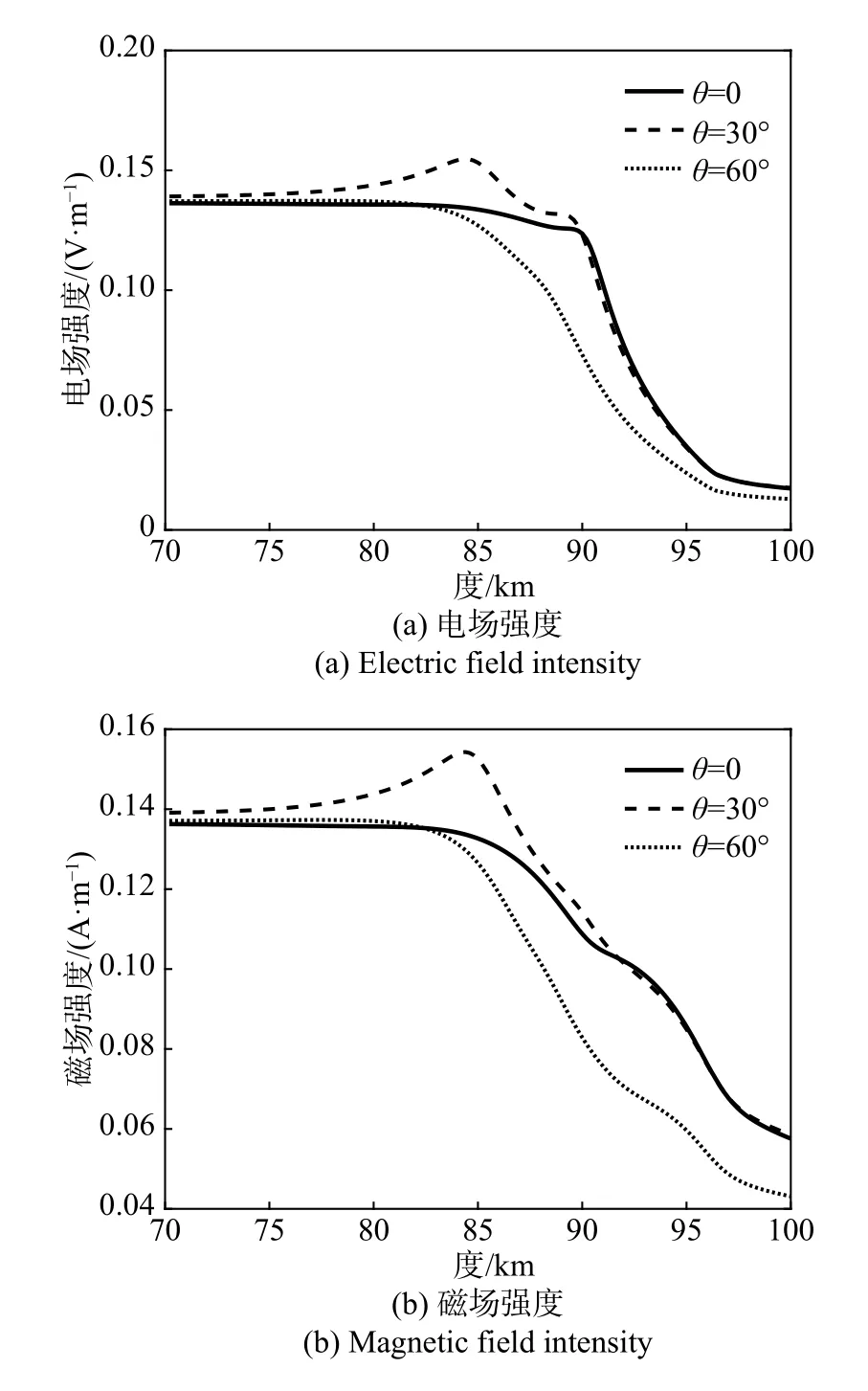
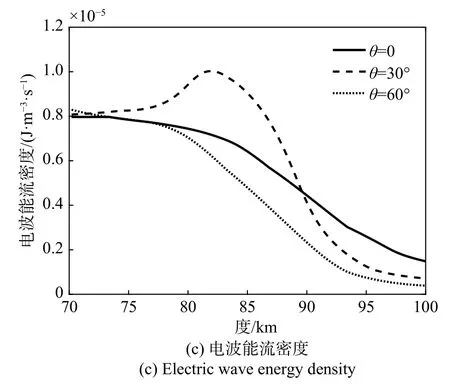
图5 电离层参数随入射角的变化Fig. 5 Variation of ionospheric parameters with incident angles

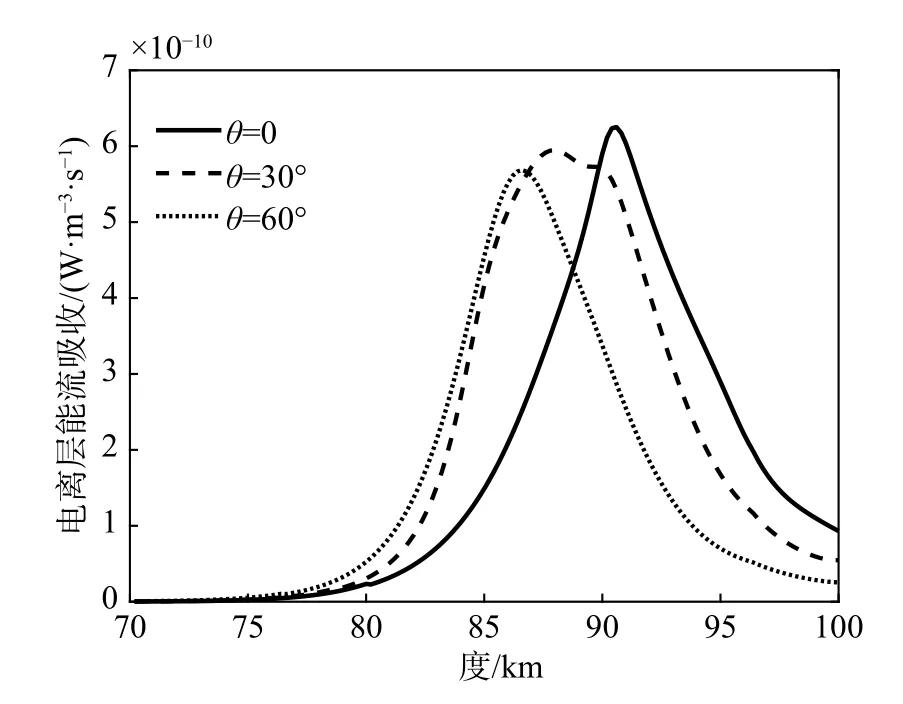
图6 不同入射角下的电离层能流吸收Fig. 6 Ionospheric energy flow absorption at different incident angles

与电离层能流吸收相对应，图7给出了电子温度的扰动情况，电子温度变化主要集中在75～95 km高度范围内. 由式(12)可知，电子温度的变化除受电离层能量变化影响外，还与背景电子浓度有关，电子浓度越低的区域电子温度变化越明显. 在入射角为30°和60°的情况下，电子温度扰动峰值都在85 km高度附近，θ= 30°时扰动幅度大一些，温度最高可达550 K，由于90 km高度电子浓度比85 km大得多，导致θ= 0时电子温度的扰动峰值很小，温度最高仅为300 K.

图8给出了不同入射角下的电子浓度与初始时刻的比值，93 km以下区域，入射角 θ越大，电子浓度主要扰动区域所在高度越低，电子浓度损失越大. θ=60°情况下，电子浓度扰动幅度最大，83 km附近电子浓度仅为初始时刻浓度的80%，θ= 30°情况下，电子浓度扰动幅度最小，85 km附近电子浓度仅损失15%. 93 km以上区域，电子浓度因电子与正离子复合效率降低而提高.

图7 不同入射角下的电子温度Fig. 7 Electron temperatures at different incident angles

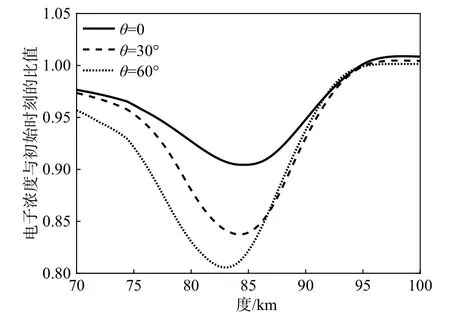
图8 不同入射角下的电子浓度与初始时刻的比值Fig. 8 Ratio of electron concentration to initial time at different incident angles

2.2.2 入射波方位角对电离层扰动的影响

在入射角θ= 30°，地磁场方向为θB=60°、φB= 0°的情况下，图9(a)、(b)分别给出了不同方位角下的电场与磁场分布. 电场的衰减主要发生在90 km以上高度，磁场的衰减主要发生在85 km以上高度. 在本文给出的初始条件下，场强随方位角增加而增大.图9(c)给出了不同入射波方位角φ下电离层能流吸收随高度的变化. 电离层对电波能流的吸收主要集中在75 km以上区域，改变方位角会影响电离层的能流吸收幅度，φ值越大，吸收峰值越大. 峰值点所在高度不受φ值变化的影响，集中在90 km高度附近，说明方位角变化不会改变电波的反射吸收高度.

图10给出了不同φ值下的电子温度扰动情况，温度的扰动主要发生在75 km以上的电离层区域.受背景电子浓度影响，电子温度的峰值点出现在87 km高度附近且位置不随φ值变化. 在φ为135°的情况下电子温度提升最明显，最高可达350 K；φ为45°时电子温度扰动幅度最小，其温度峰值仅为300 K.

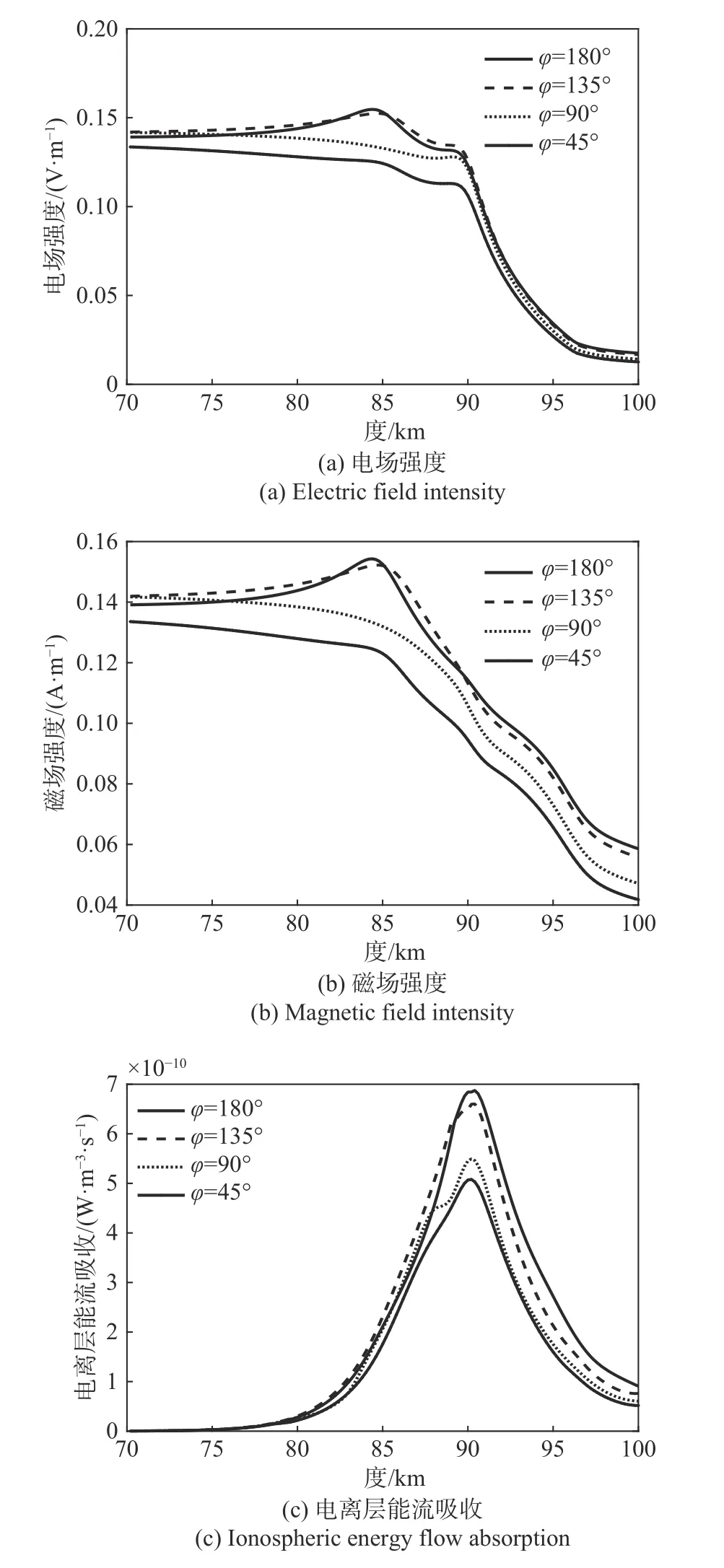
图9 电离层参数随方位角的变化Fig. 9 Variation of ionospheric parameters with azimuth angles

图11给出了不同φ值下的电子浓度扰动情况.可以看出，电子浓度扰动主要集中在85 km附近，φ为135°情况下，85 km处电子浓度损失最大，浓度仅有初始时刻的87%；φ取45°情况下，电子浓度扰动幅度最低，85 km处电子浓度仅损失10%.

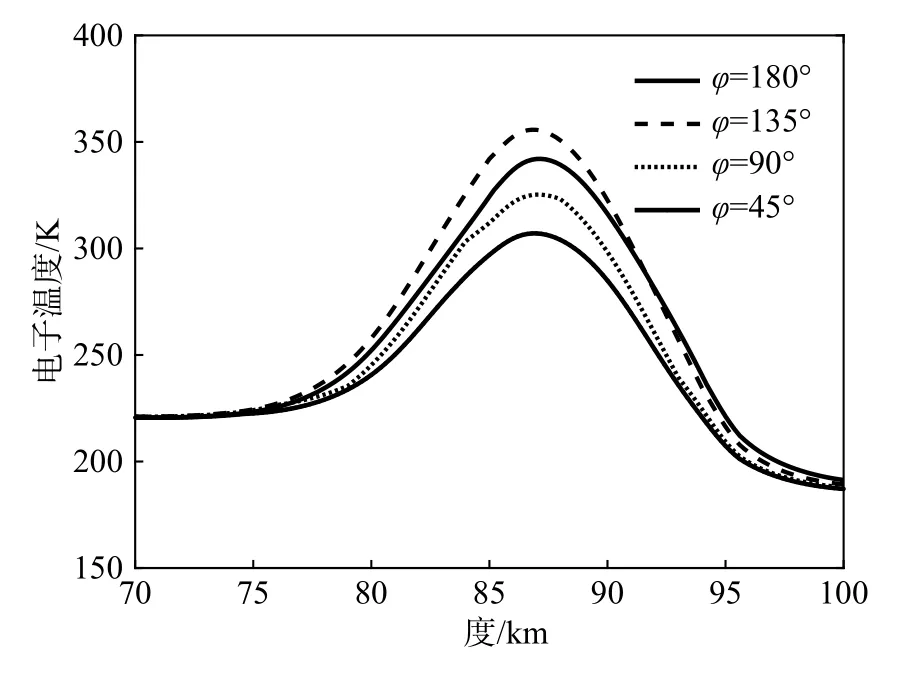
图10 不同方位角下的电子温度Fig. 10 Electronic temperature at different azimuths

图11 不同方位角下的电子浓度与初始时刻的比值Fig. 11 Ratio of electron concentration to initial time at different azimuths

2.2.3 磁倾角对电离层扰动的影响

受地理位置影响，不同纬度地区磁倾角存在较大差异，在入射波垂直向上的情况下，本节分析了磁倾角θB分别为30°、45°、60°时，基于全波法的电离层扰动情况. 图12(a)、(b)分别给出了不同磁倾角下的电场强度与磁场强度对比. 在场强衰减比较大的90 km以上高度，二者夹角越大，电场与磁场的衰减越小. 图12(c)给出了θB不同的情况下电波的能流密度. 我们发现，θB的变化对能流密度的影响主要集中在80 km以上的电离层区域. 在80～90 km高度范围内，能流密度随θB的增大而降低，特别是θB= 30°的情况下，反射、透射波相互叠加使该区域内能流密度提升明显. 90 km以上区域，θB越大电波能流衰减越慢.

图13给出了不同θB下 的电离层能流吸收情况，电波能流的吸收主要集中在80～100 km高度范围内，三种夹角下的能流吸收峰值点都在90 km高度附近. θB越 大，电离层能流吸收峰值越小，这是因为当来波方向与地磁场夹角越接近90°，波的衰减越大，电离层能流吸收越大.

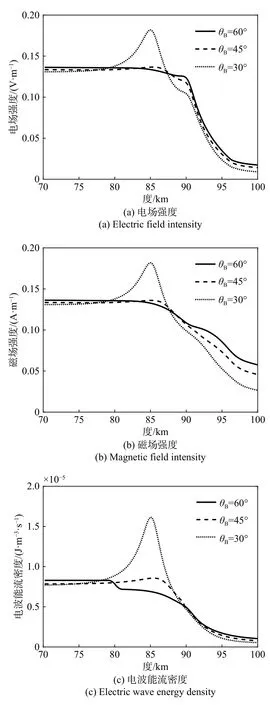
图12 电离层参数随磁倾角的变化Fig. 12 Variation of ionospheric parameters with magnetic dip angles

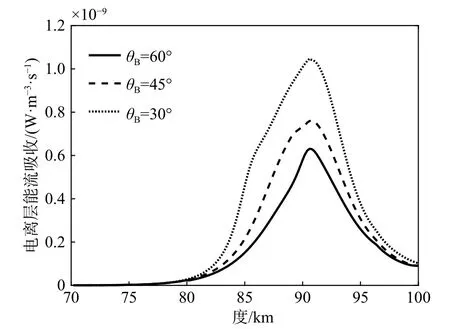
图13 不同磁倾角下的电离层能流吸收Fig. 13 Ionospheric energy flow absorption at different magnetic dip angles

图14给出了不同θB下的电子温度模型，与图8中的电离层能流吸收模型相对应，电子温度的扰动范围主要集中在80～95 km高度内，θB越小，电子温度提升越明显，θB= 30°的情况下，电子温度最高可达600 K. 不同磁倾角下，电子温度极大值点所在高度也有差异，增大θB，温度扰动的峰值点所在高度逐渐从85 km向90 km偏移.

图14 不同磁倾角下的电子温度Fig. 14 Electron temperature at different magnetic inclinations

电离层电子温度的变化会引起电子与其他粒子的附着、分离效率发生改变，图15给出了不同θB下的电子浓度变化. 对比可知，80～92 km高度内，电子温度的提高增强了中性粒子对电子的吸附效率，导致电子浓度降低，负离子浓度提高，且θB越小，电子损耗越明显，θB=30°的情况下，85 km高度处电子浓度只有初始时刻的80%. 92 km以上高度，由于电子温度的增加抑制了电子与正离子的复合效率，电子浓度由降低转变为提高.

图15 不同磁倾角下的电子浓度与初始时刻的比值Fig. 15 Ratio of electron concentration to initial time at different magnetic inclinations

2.3 不同电离层背景参量下的扰动结果对比

由于中性成分参数、化学反应系数等参量控制着电离层碰撞频率、能量损失和化学反应效率的变化，改变电离层背景参量亦会对电离层扰动情况产生影响. 本节分析了在入射波方向θ= 30°、φ= 180°，频率f= 10 kHz，地磁场方向θB= 60°、φB= 0°，强度为5 0µT情况下，不同背景参量下的电离层扰动情况.

2.3.1 化学反应系数对电离层扰动的影响

100 km以下的低电离层区域，中性成分主要为氮气和氧气，中性气体对电子的吸附是引起电子损耗的重要因素. 图16给出了中性粒子的电子附着率β对电子浓度的影响. 读图可知，随着电子附着到中性粒子的效率提高，电子浓度向减小的趋势发展. 电子浓度的变化进一步影响到电子温度的扰动情况，由图17可知，随着电子浓度的降低，电子温度在75～90 km高度范围内的扰动幅度逐渐提高.

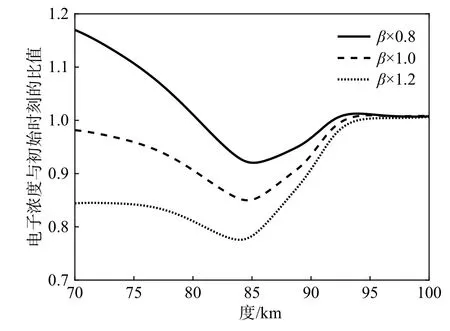
图16 不同β下的电子浓度与初始时刻的比值Fig. 16 Ratio of electron concentration to initial time at different values of β

图17 不同β下的电子温度Fig. 17 Electron temperature at different values of β

2.3.2 中性成分浓度对电离层扰动的影响

图18给出了中性成分浓度Nn分别为原值N0的0.6倍、1倍、1.4倍情况下，电子温度的扰动情况.结合式(12)和文献[15]给出的能量损失模型可知，Nn越大，能量损失项Li越大，电子温度的扰动幅度越小. 中性成分浓度的变化不会影响电子温度峰值点所在高度，电子温度的峰值点都出现在88 km附近.

图18 不同中性成分浓度下的电子温度Fig. 18 Electron temperature at different concentrations of neutral components

图19给出了不同Nn下的电子浓度扰动情况，Nn的增大同时提高了中性粒子对电子的吸附效率和电子从负离子上的脱离效率，但是前者的提升更为明显. 与图16类似，电子浓度随Nn的提高向变小的趋势发展. 高度越低，背景电子浓度越小，电子浓度的变化越明显.

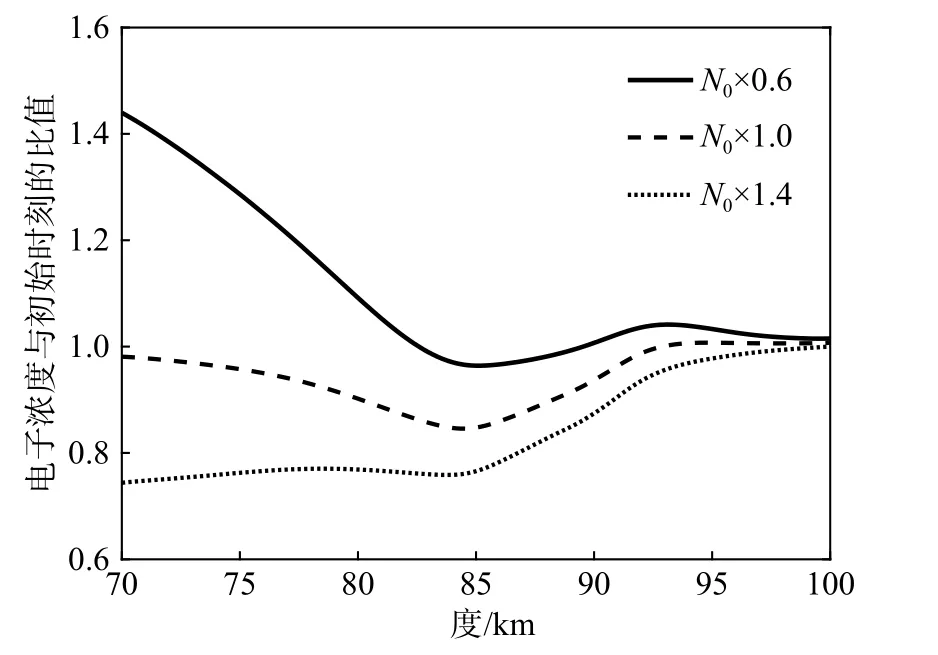
图19 不同中性成分浓度下的电子浓度与初始时刻的比值Fig. 19 Ratio of electron concentration to initial time at different concentrations of neutral components

2.3.3 中性成分温度对电离层扰动的影响

图20给出了中性成分温度Tn分别为原值T0的0.8倍、1倍、1.2倍情况下，电子温度的扰动情况.与图18相反，Tn越大电子温度的扰动幅度越大.Tn变为原值0.8倍的情况下，电子温度最大值约为325 K；Tn为原值1.2倍的情况下，电子温度最大值可提高到425 K.

图20 不同中性成分温度下的电子温度Fig. 20 Electron temperature at different neutral component temperatures

图21给出了不同Tn下的电子浓度扰动情况，可以看出在92 km以下高度，由于Tn的增大提高了中性成分对电子的吸附效率，电子浓度随Tn的增大向变小的趋势发展. 92 km以上高度，正离子浓度的增大使电子与正离子的复合效率成为影响电子浓度的重要因素，由于电子与正离子的复合效率随Tn的增大而减小，负离子上的电子脱离率随负离子浓度的提高而增大，电子浓度随Tn的增大向变大的趋势发展.

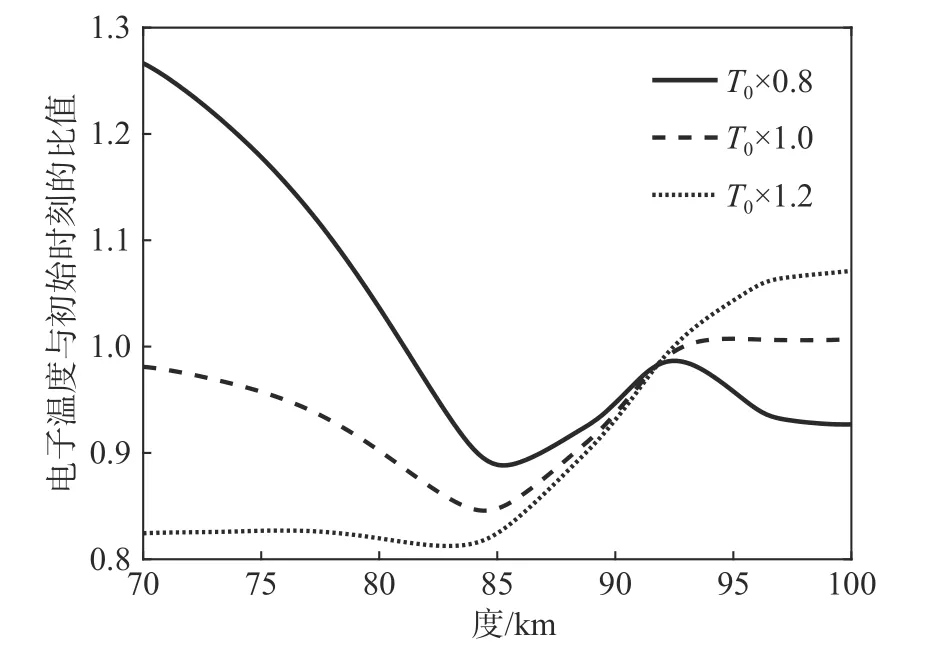
图21 不同中性成分浓度下的电子温度与初始时刻的比值Fig. 21 Ratio of electron concentration to initial time at different neutral component temperatures

3 结 论

通过全波法和波模振幅递归算法，结合Glukhov-Pasko-Inan低电离层化学反应模型，对VLF波影响下的电离层电子浓度、温度的扰动情况进行仿真. 主要成果与结论如下：

1)本文使用的全波计算方法与其他文献方法的差别在于全波法考虑到上、下行波的叠加情况. 与Rodriguez方法对比发现，在进入电离层能流相同的情况下，两种方法得到的电离层能流吸收都集中在75～100 km高度范围内，峰值点都出现在90 km高度附近. 用全波法算出的电离层能流吸收大于Rodriguez方法得到的能流吸收，进而造成电子温度、浓度扰动的不同.

2)对比了不同电波入射角、方位角、磁倾角下的电离层扰动情况，发现增大平面波入射角会导致电波能流的反射吸收高度发生改变，入射角越大，电波的反射吸收高度越低. 方位角、磁倾角的变化不会改变电波反射高度，但会对电离层能流吸收幅度造成影响，入射波与地磁场夹角越接近90°，电离层能流吸收的峰值越高. 由于电离层中电子的扰动情况还与电离层背景参量、化学反应过程有关，在多种因素调控下，电子温度、浓度的扰动幅度和扰动范围存在明显差异.

3)对比了中性成分浓度、温度等背景参量对电离层扰动的影响. 发现上述参量主要通过改变电离层能量损失项L控制电子温度的扰动幅度. 背景参量的变化还会改变离子间的化学反应效率，进而影响电子浓度的扰动情况. 不同之处在于，中性成分浓度越高，电子温度扰动幅度越小，电子浓度的损耗越大. 中性成分温度越高，电子温度扰动幅度越大，92 km以下高度电子浓度损耗越大，92 km以上高度电子浓度损耗越小.