基于神经网络的柔性机械臂反演控制方法研究

黄华

武汉铁路职业技术学院 湖北 武汉 430205

引言

柔性机械臂有耗能少、质量轻、速度快、接触冲击小等特点，应用范围广，因此大量学者将其当作研究对象。大量学者将各种控制理论用于柔性机械臂的控制。柔性机械臂本质上，是一个无穷为分布参数系统，存在非最小相位特性以及臂杆弹性振动等问题[1]。对于柔性机械臂的动力学方程，存在建模困难，测量不精确，负载非线性变化，外部干扰随机性大。

反演控制方法是核心思想是通过将复杂的非线性系统分解成多个低于原系统阶次的子系统，然后对每个子系统设计李雅普诺夫函数以及中间虚拟控制项，使得每个子系统需要依赖下一个子系统的虚拟控制项来达到稳定状态，并依次还原整个系统直到设计出最后一个子系统的控制器。但是传统的反演控制方法存在系统方程微分项膨胀的问题，每个步骤中都需虚拟控制项求导，当系统阶次较高时，虚拟控制项的高阶微分表达式无法精确得到，因此对该变量的反复求导将会提高后续步骤中控制器设计难度，这类情况经常发生在以反演控制设计为框架的自适应神经网络控制器设计当中[2]。本文将神经网络用于柔性机械臂反演控制过程中，能够实现控制无须建模的柔性机械臂反演控制，控制对象含有模型信息部分的函数逼近[3]。

1 柔性机械臂动力学模型

柔性机械臂实质上其特点有强耦合性、非线性系统、时变、多输入多输出。本文采用假设模态法进行分析，建立柔性机械臂的拉格朗日方程动力学模型。本文模型用两关节柔性臂的动力学模型如下所示：

其中，q是柔性关节位置，θ是电动机转动角度，I表示柔性臂转动惯量和J是电机的转动惯量，K代表柔性机械臂的刚度系数，K和柔性机械臂弹性刚度成正比，当K越大则柔性臂弹性刚度大，此时柔性小。dt是假设的外界干扰和模型不确定参数，M、l、g分别表示柔性机械臂质量、柔性机械臂重心到关节的长度、重力加速度，u表示电机控制输入力矩。

取状态变量：

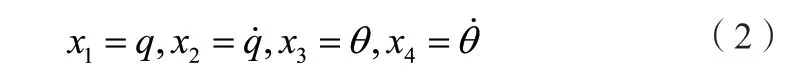
则式（1）可以写成状态方程的形式：

2 反演控制器的设计与分析

要对被控制系统实现准确的自动控制，利用反演法可以非常适用于不确定非线性系统的鲁棒控制和自适应控制。尤其是针对柔性机械臂这种存在干扰不确定性，难以满足匹配条件的复杂系统。

3 神经网络反演控制的设计与分析

4 柔性机械臂系统仿真

斯函数中心点矢量。取 。通过matlab仿真结果如下。

图2 系统各个状态的观测值

分析图1可知，在神经网络算法下的柔性机械臂反演控制可以实现机械臂的良好轨迹跟踪性，并且跟踪误差小。分析图2，可以看出系统的各个状态变量的估计误差渐进趋近于零，可知本文设计的控制策略有效。

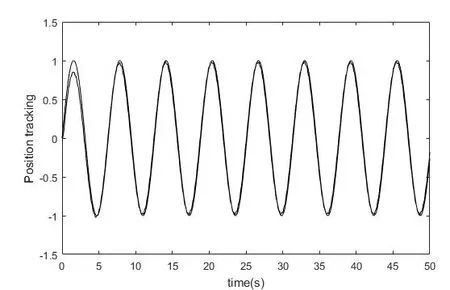
图1 柔性机械臂位置跟踪

5 结束语

针对柔性机械臂这样复杂的动力学方程模型，本文研究了反演法用于柔性机械臂控制中，同时考虑到柔性机械臂建模困难。将神经网络与反演控制结合起来，综合考虑控制律和自适应律，使柔性机械臂整个闭环系统达到期望的动静态性能，同时能够实现无须精确建模的柔性机械臂控制，实现被控对象中含有模型信息部分的函数逼近[4]。通过仿真分析，可以得知本文将基于神经网络算法的反演控制方法用于柔性机械臂的方法是有效的。不论是哪种控制方法，均存在两面性，既有优点也有缺陷，因此需要在后续的柔性机械臂的控制研究过程中应该根据柔性机械臂实际适用场合，采取有针对性的控制方法，发挥各种控制方法的优势达到最佳的控制效果。