考虑高压直流接入的电网调峰优化方法研究

邢超，和鹏，刘明群，奚鑫泽，李胜男

（云南电网有限责任公司电力科学研究院，昆明 650217）

0 前言

随着高压直流接入电网，导致电网的运行情况更加复杂，调峰问题进一步加剧，亟需研究高压直流接入对电网调峰的影响及其应对措施[1]。区域电网的调峰困境日渐突出，对各级电力系统安全稳定的影响不容小视[2-5]。目前，在高压直流接入的电网调峰评估方法中，高压直流一般按照有功功率的运行方式进行处理，并且以备用容量或者调峰盈余作为指标来评估电网的调峰能力[6-13]。以备用容量评估电网的调峰能力，即先求出电网所能提供的备用容量，再将系统所能提供的备用容量和所需求的备用容量进行对比，从而评估电网调峰平衡情况的优劣。以调峰盈余评估电网的调峰能力，则是根据电源的调峰能力、负荷峰谷差和备用容量求出调峰盈余，根据调峰盈余容量的大小对电网的调峰能力进行评估[14-18]。

文献[19]提出基于熵权属性识别模型的电力系统调峰方案评估方法体系。文献[20]从电网、电源和高载能负荷三个方面提出了表征电力节能的指标，然后基于综合模糊评价法进行综合评估。文献[21]提出一种综合考虑系统运行成本以及常规机组低谷时刻负调峰能力的多目标机组组合优化模型。文献[22]利用年弃风比例、年利用小时数、年弃风电量月分布、年弃风电量峰谷分布等各类数据，来反映水平年风电弃风情况。文献[23]建立了以有功损耗最小为目标，计及机组爬坡速率约束以及系统安全约束的优化调度模型，制定了高压直流送不同风电比例情况下电网的调峰方案。

传统的评估方法中仅以备用容量或调峰盈余作为单一评价指标对调峰方案进行评估，难以适应复杂调峰运行方式的需求，无法对电网的调峰能力做出全面、科学的评价。本文采用了一种新的评估方法，考虑高峰时期调峰盈余和低谷时期弃电量两个评估指标，以调峰盈余隶属度函数和弃电量隶属度函数之和构建综合评价模型，以综合隶属度函数最大化为目标来评价高压直流接入后电网的调峰能力，逐月校核调峰平衡情况，根据校核结果分月制定高压直流的调峰运行方式。

1 调峰评估指标

高压直流接入电网后，考虑负荷高峰期调峰盈余和最大、最小调峰盈余，引入调峰盈余隶属度函数；同时对于高压直流的接入会使电网在多个月份的低谷时段存在调峰缺额的情况，引入弃电量所对应的隶属度函数。

1.1 调峰盈余隶属度函数

以调峰盈余隶属度函数评估电网的调峰能力，首先根据高压直流所传输的最大、最小电能，求出最小调峰盈余和最大调峰盈余；再将调峰盈余容量减去最小调峰盈余；最后除以最大、最小调峰盈余的差值，从而求出调峰盈余隶属度函数。具体计算过程如下：

高压直流传输最小电能时最大调峰盈余容量如式（1）所示。

高压直流传输最大电能时最小调峰盈余容量如式（2）所示。

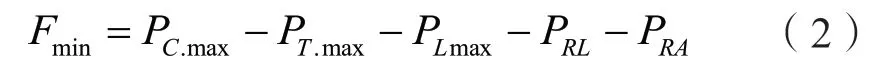
高压直流不同运行方式下的调峰盈余如式（3）所示。

式中：Fmax和Fmin分别表示最大调峰盈余和最小调峰盈余；Fi表示第i个高压直流运行方式下的调峰盈余；PLmax表示系统的最高发电负荷；PC.max和PC.min分别表示系统所有出力可控电源同一时段最大、最小可调出力；PT.i为第i个高压直流运行方式下高压直流传输的电能；PT.max和PT.min分别为高压直流传输的最大、最小电能；PRL为负荷备用(热备用)；PRA为事故备用(热备用)。

由此可得调峰盈余隶属度函数表达式如式（4）所示。

式中：ηi为第i个高压直流运行方式下调峰盈余隶属度函数。

1.2 弃电量隶属度函数

当负荷低谷时期调峰盈余不足时，引入弃电量隶属度函数来评估电网的调峰能力。弃电量的定义如下：

图1中的阴影部分的面积即为典型日低谷盈余不足情况下的弃电量。

图1 典型日弃电量示意图

典型日弃电量E定义式如式(5)所示。

式中：t1和t2分别为典型日负荷低于最低出力的起始时间和终止时间；p为低谷最小出力；f(x)为负荷曲线的数学表达式。

通过典型日弃电量得到典型月弃电量P，如式（6）所示。

式中：E为典型日弃电量；n为该月份的天数；α为弃电量系数。

高压直流传输最小电能时，典型日弃电量最大值表达式如（7）所示。

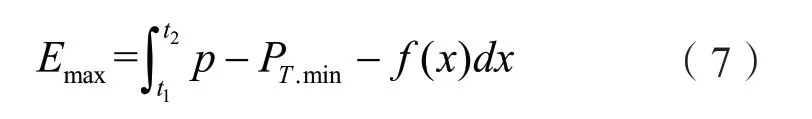
高压直流传输最大电能时，典型日弃电量最小值表达式如(8)所示。

高压直流不同运行方式下典型日弃电量表达式如(9)所示。

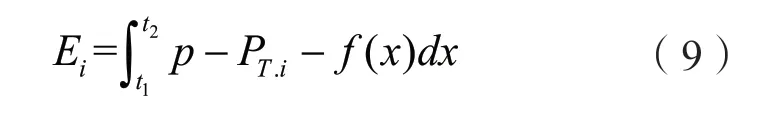
式中：Emax和Emin分别为典型日最大弃电量和最小弃电量；Ei为第i个高压直流运行方式下的典型日弃电量；PT.max和PT.min分别为高压直流传输的最大、最小电能；PT.i为第i个高压直流运行方式下高压直流传输的电能。

高压直流传输最小电能时，典型月弃电量最大值如（10）所示。

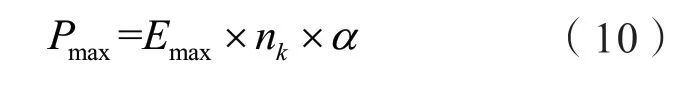
高压直流传输最大电能时，典型月弃电量最小值如式（11）所示。

高压直流不同运行方式下典型月弃电量如式（12）所示。

式中：Pmax和Pmin分别为典型月最大弃电量和最小弃电量；Pi为第i个高压直流运行方式下的典型月弃电量；nk为第k月的天数。

由此可得弃电量隶属度函数如（13）所示。

式中：ξi为第i个高压运行方式下弃电量隶属度函数。

2 评估方法流程及数学模型

本文将高压直流纳入调峰体系，考虑高压直流多种运行方式，基于多目标分段建模理论，构建以调峰盈余隶属度函数和弃电量隶属度函数为指标的综合评估模型，提出一种以综合隶属度函数最大化为目标的高压直流调峰评估方法。该方法将分月制定高压直流调峰方案，并利用综合隶属度函数对调峰方案进行评估，从而选取最优的调峰方案。评估思路为：计算调峰盈余隶属度函数和弃电量隶属度函数，通过比较两个隶属度函数之和的大小来评价不同调峰方案的优劣。其求解流程如图2所示。

图2 调峰评估方法流程图

从每年的1月开始，根据高压直流的最大、最小传输电能，计算出当月负荷高峰时段的最大、最小调峰盈余、高压直流不同运行方式下的调峰盈余和负荷低谷时段最大、最小弃电量、高压直流不同运行方式下的弃电量。从而计算出当月不同运行方式下的调峰盈余隶属度函数和弃电量隶属度函数。比较不同运行方式下的综合隶属度函数，以综合隶属度函数最大值所对应的调峰方案作为当月的调峰方案。对1月至12月进行逐月校核，分别得到各个月对应的最优调峰方案。

基于分段建模的高压直流运行曲线优化策略数学模型如（14）所示。

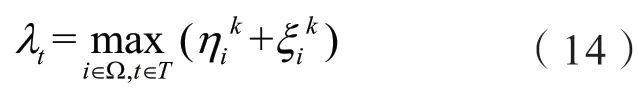
式中：表示第k月中i个高压直流运行方式下的综合隶属度函数；Ω为调峰方案个数的取值空间，T为月份的取值空间，分别为第k月第i个高压直流运行方式下的调峰英语隶属度函数和弃电量隶属度函数。

3 调峰方案及仿真实例

利用本文中的调峰评估方法对永富高压直流接入云南电网的调峰情况进行具体分析。

3.1 永富高压直流运行方案

2016年，永富高压直流工程建成投产，永富高压输送电力容量最小为150 MW，最大为3000 MW。结合云南电网的负荷需求以及永富高压直流的送电能力，将永富高压直流的运行方案设置五种运行方式。

云南电网0点至8点为负荷低谷时段，8点至24点为负荷高峰时段。

方式一：永富直流按高峰低谷输送相同电能，即1500 MW。

方式二：永富直流在0点-8点按1200 MW输送电能，8点-24点按1800 MW输送电能。

方式三：永富直流在0点-8点按900 MW输送电能，8点-24点按2100 MW输送电能。

方式四：永富直流在0点-8点按600 MW输送电能，8点-24点按2400 MW输送电能。

方式五：永富直流在0点-8点按300 MW输送电能，8点-24点按2700 MW输送电能。

3.2 2017年仿真实例

根据2017年云南电网运行数据，算出2017年云南电网调峰盈余，同时做出调峰盈余对比图，如图3所示。

图3 2017年云南电网调峰盈余对比图

由图3可知：在永富高压直流采取相同的运行方式情况下，对比不同月份的调峰盈余，最大的调峰盈余出现在七月。

在同一月份中，对比永富高压直流采取的不同运行方式，最大的调峰盈余出现在方式一。

根据对云南电网不同月份最小负荷典型日曲线的分析研究，弃电量系数近似取值为1-3月取0.23，4-6月取0.3，7-9月取0.25，10-12月取0.2。根据前述弃电量计算方法，得到2017年云南电网各月份的弃电量，同时做出弃电量对比图，如图4所示。

图4 云南电网2017年份月弃电量对比图(亿kWh)

由4可知：在永富高压直流采取相同的运行方式情况下，对比不同月份的弃电量，最大的弃电量出现在九月。

在同一月份中，对比永富高压直流采取的不同运行方式，最大的弃电量出现在方式一。

由以上数据计算出调峰盈余隶属度函数、弃电量隶属度函数以及综合隶属度函数，同时做出2017年云南电网不同月份隶属度函数的对比图，如图5、图6、图7所示。

图5 调峰盈余隶属度函数对比图

图6 弃电量隶属度函数对比图

由图5可知：在2017年云南电网运行的每个月中，方式一的调峰盈余隶属度函数最大，同时都为0.5263；而方式五的调峰盈余隶属度函数最小，同时都为0.1053。在永富直流的每种运行方式中，12个月份的调峰盈余隶属度函数大小都相同，五种方式分别为0.5263，0.4211，0.3151，0.2105，0.1053。

由图6可知：在永富高压直流采取相同的运行方式情况下，对比不同的月份的弃电量隶属度函数，最大值出现在2月。

在同一月份中，对比永富高压直流采取的不同运行方式，最大的弃电量隶属度函数出现在方式一。由图7可知：在2017年云南电网运行的每个月中，方式一的综合隶属度函数最大。因此2017年云南电网全年采取方式一进行电网调峰，即永富高压直流在高峰和低谷输送1500 MW电能。采取该方式调峰，云南电网全年都能够满足高峰低谷负荷需求，调峰效果能够达到最好，使得云南电网经济稳定运行。

图7 综合隶属度函数对比图

4 结束语

本文针对高压直流接入对电网调峰产生的影响，在分析传统调峰评估方法的基础上，引入了调峰盈余隶属度函数和弃电量隶属度函数，从而提出了一种新的调峰评估方法，并在该评估方法下对永富高压接入后云南电网2017年的调峰情况进行实例计算，得到了以下结论：

1）永富高压直流采取运行方式一，即在高峰期和低谷期同时输送1500 MW电能，能够满足2017年云南电网全年负荷需求，使得调峰效果达到最好。

2）对于考虑高压直流接入的电网，能够采用调峰盈余和弃电量两个指标来对调峰问题进行评估，从而得出最优的调峰方案。