15 MeV/nucleon 40Ca+12C反应中α粒子的能谱分布研究

牛丹丹，张苏雅拉吐，王金成

（1.内蒙古民族大学 数理学院，内蒙古 通辽028043；2.内蒙古民族大学 核物理研究所，内蒙古 通辽028043）

近几十年来，重离子核反应一直是研究核结构和核反应动力学性质的重要途径，除通过实验之外，理论模型也是非常重要的研究方式.由于重离子核反应机制的复杂性，对反应中出现的机制和现象，比如半渗透、多重碎裂过程等，通过模型模拟出一个清晰的物理图像是十分重要的.目前应用广泛的输运模型如下［1-2］：分子动力学模型（BUU）和（BNV）、量子分子动力学（QMD）模型以及扩展版本的量子分子动力学（EQMD）模型、约束分子动力学（CoMD）模型、反对称化的分子动力学（AMD）模型及费米子分子动力学（FMD）模型.每一个模型都有自己的成功之处和适用范围［3］.AMD模型用与时间相关的波函数描述核系统，在核反应随时间演化过程中严格遵从泡利阻塞［4］.AMD模型广泛地应用于核反应和核结构领域中［5］，但往往忽略了不同版本的区别与差异.笔者利用AMD中两种不同版本对40Ca轰击12C的核反应过程进行研究，目前该系统还没有相关的实验数据，因此这能够为使用AMD不同模型在研究核反应与核结构领域提供理论依据.

1 AMD模型简介

AMD模型曾用来研究费米能区重离子核反应中的碎片产物，而且能够很好的重现实验结果的整体特征［6-9］.在重离子反应中，存在各种产生碎片的机制，比如气泡破碎、聚结、液-气相变、颈段碎裂、参与者-旁观者机制等.在解释核反应早期的碎片产物时动力学是至关重要的，所以使用动力学模型如AMD模型是必要的.

AMD模型是量子分子动力学（QMD）的反对称化版本.AMD模型中随时间演化的波函数能够描述核的量子效应，原子核稳定的基态是通过摩擦冷却方法构造的［10］.

对于N个核子的反应系统，用斯莱特行列式（Slater determinant）表示N个高斯波包构成的波函数［11］：

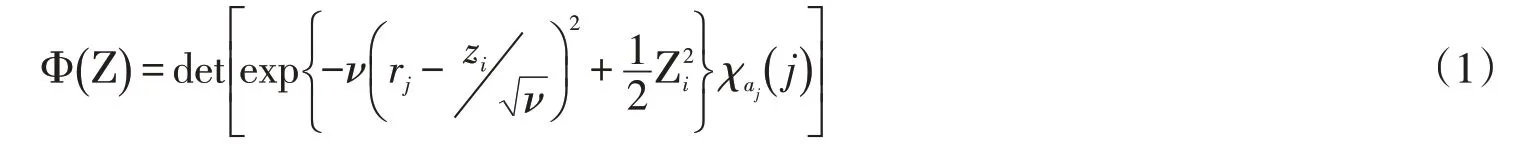
其中，复变量Ζ={Ζi;i=1,…,N}，Ζi表示波包的矩心，可以表示为：

AMD模型中，波包的宽度参数ν通常取ν=0.16 fm-2，χaj(j)为自旋与同位旋态.

由于反对称效应，Di和Ki不再对应于每个核子的坐标和动量，Z的时间演化由时间相关的变分原理和核子与核子之间的随机碰撞中计算得到.从时间相关的变分原理中得到Z的运动方程为：

其中，Ciσjτ为哈密顿矩阵，表示为：

H为减去质心系中零点振荡时伪动能后的哈密顿量期望值.由于AMD反对称效应，Di和Ki不能再表示核子的坐标和动量，因此考虑通过物理坐标W={Wi}来描述核子核子碰撞，该物理坐标定义为：

其中,Qij定义为：

在采用了高斯波包的分子动力学中，在t=t0时刻，具有真实物理坐标Ri和Pi的第i个核子在相空间的高斯波函数表示为：

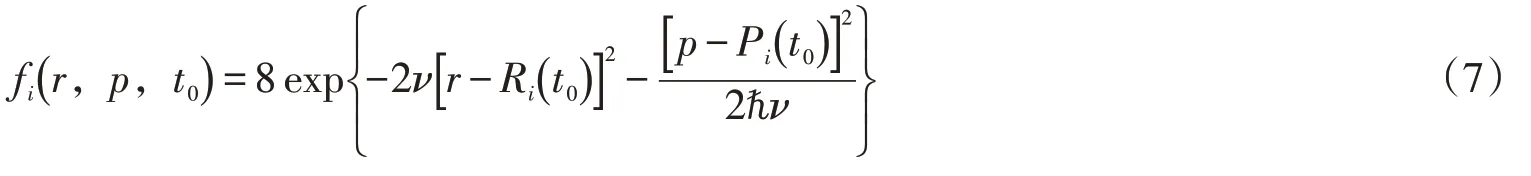
则总的一体函数分布便为所有fi的和.只有物理坐标为

时，用简单的高斯波包来描述核子才是近似有效的.

2 AMD版本区别

为了描述中能重离子碰撞中的高能质子发射，LIN等［12］在核子-核子碰撞过程中精确地考虑了核子的费米运动，这个对AMD模型做了进一步拓展的模型就叫做AMD-FM.

AMD-FM模型中，当碰撞距离大于两个核子的间距时，根据波包中心附近的高斯分布给出的动量不确定性就会增加，这种处理方法与其他微观运输模型中的做法完全不同.在其他运输模型中，核子的费米运动只在初始核中给了一次，对于每一次碰撞都重复该过程.

3 AMD模拟结果

由于AMD模型可以很好的再现中低能核反应的物理过程和实验数据［12-13］.因此可以用AMD来研究40Ca+12C在入射能E=15 MeV/nucleon的碰撞中的碎裂现象.根据AMD理论计算，本次模型模拟中该反应的碰撞过程，提取出α粒子的能谱分布.其中AMD理论计算的事件演化时间为t=800 fm·c-1，碰撞参数范围是0~8 fm，在相空间中的并合的半径Rc=5 fm.在下面的AMD计算中均采用该条件.参考美国Texas A&M大学加速器研究所实验，探测器分别放在靶的周围，与束流所成的角度分别为2.5°、7.5°、12.5°、17.5°、22.5°、27.5°、32.5°、37.5°，误差为2.5°.本次模型模拟中为了更好地与实验情况相一致，在模拟中均采用这些角度.下面给出40Ca+12C反应中α粒子的两种AMD模型版本计算的不同过程的结果.此外，由于核反应过程（初级反应过程）一般需要的时间量级为10-21s（100 fm·c-1），核反应之后，不稳定的原子核会处于激发态，然后经过激发冷却过程（次级衰变）变成稳定的原子核，而实验中用于探测α的探测器与发生核反应的位置相隔较远，因此需要研究次级衰变对初级反应过程的影响.通常用AMD模型结合Gemini统计衰变模型来研究该影响［13］.

3.1 α粒子初级衰变

图1中给出了α粒子在初级反应过程中的2种版本的对比，其中空心圆为AMD模型，实心方块为AMD-FM模型.

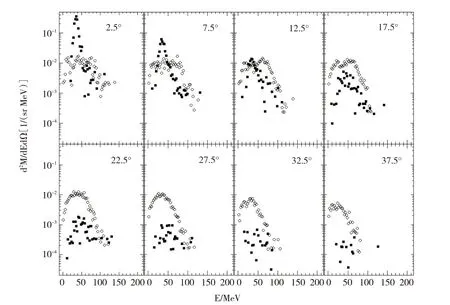
图1 入射能为15 MeV/nucleon的40Ca+12C初级衰变能谱（Z=2，A=4）Fig.140Ca+12C primary decay energy spectrum of incident energy of 15 MeV/nucleon（Z=2，A=4）

3.2 α粒子次级衰变

图2中给出了α粒子在次级衰变过程中的2种版本的对比，其中空心圆为AMD模型，实心方块为AMD-FM模型.

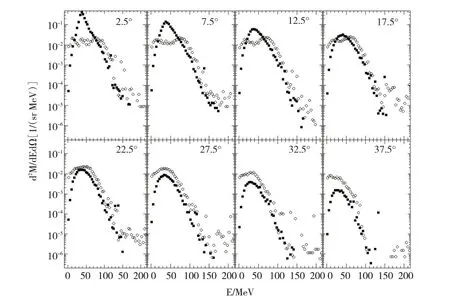
图2 入射能为15 MeV/nucleon的40Ca+12C次级衰变能谱（Z=2，A=4）Fig.240Ca+12C secondary decay energy spectrum of incident energy of 15 MeV/nucleon(Z=2，A=4)

4 AMD结果分析

从图1和图2可以看出，AMD和AMD-FM在初级反应过程和次级衰变过程中，模拟得到的α粒子能谱形状差异非常大.AMD可以清晰地分辨出2个峰.这是由于核反应过程中存在着与弹核相似的α粒子，主要来自于类弹碎片（PLF），能量较高；以及与靶核相似的α粒子，主要来自于类靶碎片（TLF），能量相对较低.而AMD-FM则无法区分α粒子的来源，这是由于AMD-FM会使核反应中的核阻止本领增加［12］.

另外，还可以看到，AMD和AMD-FM模拟得到的α粒子能谱在次级衰变与初级反应过程的形状相似，表明次级衰变对α粒子能谱分布影响较小.

5 结束语

利用反对称化分子动力学模型（AMD），分别采用AMD和AMD-FM两种系统模拟计算了入射能为15 MeV/nucleon的40Ca轰击12C反应初级反应和次级衰变过程，且AMD模型广泛地应用于核反应和核结构领域中，经过对比结果，2种版本有明显区别，这为以后运用该模型来做相关的理论研究提供了基础.