多功能雷达脉冲列的语义编码与模型重建

刘章孟 袁 硕 康仕乾

(国防科技大学电子科学学院 长沙 410073)

1 引言

多功能雷达是指能够执行多种功能的雷达，常用功能包括搜索、跟踪等[1]。电子器件水平的提高、信号处理能力的增强等因素推动雷达从传统单一功能向多功能发展，雷达功能的多样性还常常与雷达波束的强方向性、雷达参数的灵活捷变特性综合使用，构成了多功能相控阵雷达[2]。随着对目标探测需求的持续增长，在同一部雷达中综合多种功能已成为大多数新型雷达的基本设计理念，对于高成本的现代先进雷达尤其如此[3]。

借助电子侦察手段截获和分析雷达信号以实现目标发现、跟踪和识别，是电子情报分析、电磁态势感知的重要途径[4]，其中多功能雷达是雷达侦察领域的重难点对象。深入研究多功能雷达的信号特点、行为规律，对于精确掌握重要的目标情报十分必要。多功能雷达信号具有更加复杂的层次化时序结构和变化规律，既包含了执行特定功能时脉组内部多个脉冲的编排方式，也包含了在搜索、跟踪等不同任务之间切换的状态转移规律[5–7]，且其低截获概率特性造成了侦察截获信号的严重残缺，这些因素都显著增大了从电子侦察脉冲列中获得关于雷达工作状态信息的难度[7]。

一直以来，多功能雷达工作模式分析问题的重要性得到了电子侦察领域研究人员的广泛认同，但其难度极大阻碍了对该问题的解决进程。与这一问题密切相关的研究成果是加拿大学者Visnevski等人[5,6]在2007年左右所做的研究工作。他们对多功能雷达信号进行层次化建模，并提出句法分析方法解决对雷达脉冲列的细致分析问题。该成果具有较强的理论性，而且结合特定雷达进行了可行性验证[6]。然而，对多功能雷达的信号建模是一个正向分析过程，需要提前获得关于雷达工作方式和信号结构的充分的先验信息，这一要求在雷达侦察领域通常是无法满足的。

从电子侦察的角度来看，基于侦察系统截获的大量多功能雷达脉冲，如果要构建一个时序模型对这些脉冲的关联关系进行刻画，则该模型的形式存在无穷多种可能性。但是，从雷达设计者的角度来看，雷达是为完成特定的目标探测、跟踪等任务服务的，而且在整个工作过程中都在重复执行类似的辐射行为，以实现对广大空域的持续覆盖。因此，在错综复杂的雷达脉冲列内部，应当隐藏着一个简洁、紧凑的时序模型，用于控制不同功能脉组的执行过程，以及每种功能的信号结构等。如何从电子侦察的视角重建雷达脉冲列的时序模型，对精确掌握雷达情报并支持雷达对抗等应用具有重大现实意义。

近年来，国内电子侦察领域的一些学者探索了多功能雷达信号时序模型的分析、重建与应用等问题。方佳璐[8]使用滑动时间窗对具有复杂时序规律的脉冲列进行了时域截取和模式识别，并深入研究了雷达工作模式的动态识别、增量识别等问题，但没有确切分析脉冲列中多个连续脉冲之间的关联关系。Li等人[9]引入深度学习技术对多功能雷达的脉组结构进行了分析，并成功实现了多功能雷达工作模式识别，但深度学习模型训练所需的雷达工作模式标签在实际场景中往往难以获得。欧健、林令民等人[10–12]以多功能雷达信号的层次化模型为基本依据，借助预测状态表示(Predictive State Representation,PSR)和隐马尔可夫模型(Hidden Markov Model,HMM)等工具，系统研究了多功能雷达行为特征表征、建模、模式辨识和序列预测等问题。这些成果具有较强的原创性，但是与雷达层次化信号模型相关的研究内容大多以雷达脉组的成功提取作为前提，与大多数实际应用需求并不完全吻合。

本文遵循模型简洁性(奥卡姆剃刀定律)这一基本原则[13]，基于雷达侦察脉冲列重建多功能雷达的层次化信号模型，着重解决两个问题：一是雷达脉冲列中基本信息单元––脉组的提取，二是脉组切换模型的重建。本文在描述多功能雷达脉冲列时序结构的基础上，首先借鉴信息论与编码理论定义了雷达脉冲列的复杂度；随后，依据复杂度最小化准则对雷达脉冲列进行编码，最终所得的编码字典中各码字的内容对应于多功能雷达执行各种功能的基本脉组结构；最后，基于脉组提取结果和以此为基础的雷达脉冲列编码序列，估计雷达不同状态之间的切换规律，进而完整重建多功能雷达脉冲列的层次化模型。在模型构建、方法介绍和仿真实验部分，本文均以具有2层信号模型的相对简单的多功能雷达为例进行说明，以简化叙述、增强可读性，并在结束语中进行了补充说明，阐述本文方法扩展应用至体制更加复杂的多功能雷达的基本思路。

2 多功能雷达脉冲列描述

通常情况下，多功能雷达按照特定规律顺次辐射脉冲组合以执行目标搜索、跟踪等多种任务，每种功能对应脉组内部包含具有特定时序结构的脉冲组合。图1示意了多功能相控阵雷达的工作方式，这一工作特点造成了多功能雷达脉冲列在时序上的层次化结构。

图1 多功能雷达的工作模式示意图Fig.1 Schematic diagram of the working mode of multifunctional radar

在底层，由不同的脉冲组合构成基本的信息单元––脉组，用于执行特定方向和距离上的目标搜索、跟踪等任务，各脉组通常具有确定的时序结构，也可能包含少量的捷变参数。对于空对地、空对海雷达，由于存在消除地杂波、海杂波等需求，脉组内部可能具有更加复杂的层次化结构[6]。在顶层，雷达根据预设的任务执行规则依次发射不同功能脉组，先进雷达还可以根据实际的任务需要，在局部时段内灵活地调度和调整工作进程，但在总体上，很多多功能雷达的相邻脉组之间的切换规律在整体上表现为一个概率模型。

2.1 多功能雷达脉冲列的层次化模型

多功能雷达为执行目标探测任务，持续向空间辐射电磁脉冲，脉冲的基本参数包括载频、脉宽、发射时间等[4]，其中各脉冲的发射时间构成了脉冲列的时序结构。多功能雷达针对特定距离和方位上的目标执行一次搜索或跟踪等任务的脉冲组合称为脉组，是多功能雷达脉冲列的基本信息单元。以图1中雷达在机载侦察接收机方向上发射的脉组为例，该脉组结构由多个脉冲的参数和各脉冲之间的时序规律构成，如图2所示。

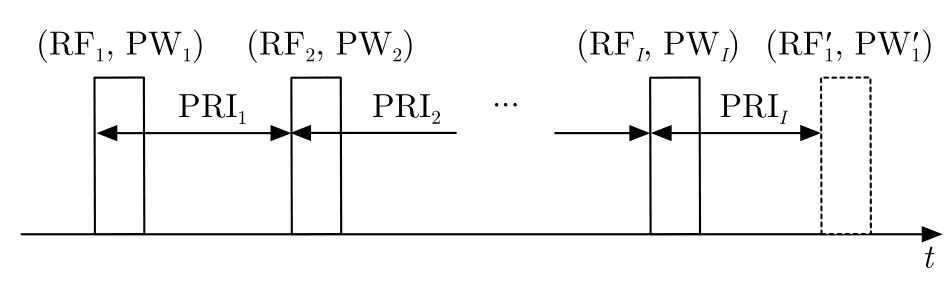
图2 多功能雷达的脉组结构Fig.2 Pulse group structure of multifunctional radar

图2中实线矩形表示当前状态脉组中包含的I个脉冲，脉冲列的载频、脉宽参数依次为(RF1,PW1),(RF2,PW2),···,(RFI,PWI)，依据实际截获数据情况，还可以包含脉幅、调制信息等相关参数；脉组内部的时序信息可表示为脉间间隔(Pulse Repetition Interval,PRI)序列(PRI1,PRI2,···,PRII)；虚线矩形表示下一个状态脉组的第1个脉冲，该脉冲与当前脉组最后一个脉冲之间构成PRI序列的最后一个元素PRII。图2中脉组的时序表示形式为

在脉组单元的基础之上，多功能雷达在不同工作状态之间持续切换，雷达脉冲序列x因此表现为连续的脉组序列···abac···，其中a,b和c等分别是用于执行目标搜索、跟踪等任务的脉组，是上述脉组表达式α的具象化形式，而每个脉组中分别包含若干个时域离散脉冲，即a=a1a2···aIa,b=b1b2···bIb和c=c1c2···cIc等，其中Ia,Ib和Ic分别表示对应脉组的脉冲数，ai,bi和ci是上述脉冲信息单元α的具象化形式[5–7]。基于该模型，雷达辐射脉冲列可表示为

上述脉冲列模型还可用图3所示的包含两个层级的层次化结构形象表示，顶层刻画了不同模式对应脉组(a,b,c等)之间的切换过程。为方便表述，本文将顶层模型简化为一个马尔可夫过程[5]，即每个时刻的雷达状态仅由前一个状态决定，状态之间的转移过程由矩阵T控制；底层结构由各脉组对应的脉冲序列串连而成，对应于式(2)中脉冲列的第2种表示形式。

状态转移矩阵T是一个概率模型，表示多功能雷达在不同状态之间切换的统计规律。以包含3种功能的多功能雷达为例，状态转移概率矩阵可表示为

其中，pα→β(α,β ∈{a,b,c})表示当多功能雷达当前状态为α时，下一时刻切换至状态β的概率。该矩阵满足T ×1=1,1表示全1列向量。

上述2层脉冲列结构模型是对实际多功能雷达信号模型的简化结果。一方面，对于对地、对海探测的多功能雷达，以及目标跟踪雷达等，由于它们在设计过程中包含了消除杂波、盲速、盲距等方面因素的考虑，其每个功能脉组内部又可划分为多个子脉组，雷达脉冲列模型描述为3层结构更为确切，例如文献[6]所介绍的“水星”雷达。另一方面，先进多功能雷达不同状态之间的转换过程是一个由可变阶数马尔可夫模型构成的混合过程，实现空域覆盖的重复性目标搜索过程具有1阶结构，执行从目标搜索到目标确认、跟踪的过程具有高阶结构。本文针对具有2层结构的多功能雷达脉冲列进行语义编码原理分析和模型重建方法介绍，主要是为了简化描述、增强直观性，该方法可以经过适当修正之后应用于具有更复杂层次结构的多功能雷达脉冲列。

在雷达脉冲列的层次化结构中，蕴含了与雷达工作模式相关的丰富物理含义。对照多功能雷达脉冲列的句法模型[5,6]，图4给出了更具一般性的3层多功能雷达脉冲列模型，图中脉冲组合(用小写字母a,b,c,x,y等表示)对应于雷达字，每个雷达字用于获取特定的目标信息；多个雷达字串联构成雷达短语(用大写字母A表示)，用于执行目标搜索、跟踪等特定功能。多功能雷达脉冲列的语义模型，指的是雷达信号设计和雷达功能执行规则在雷达脉组及其切换过程等时域特征上的呈现方式。如果将雷达脉冲列看作一个字符串，则通过从中提炼各雷达字、雷达短语的构成及使用规律，既可以实现对雷达脉冲列的结构分析和模型重建，也可以反映各雷达的工作特点。在缺少雷达工作模式先验信息的条件下，从电子侦察的视角重建雷达脉冲列的层次化结构和语义信息，是本文的研究目的。

2.2 多功能雷达脉冲列侦察模型

多功能雷达在开机状态下持续向外发射脉冲，构成了式(2)所示的时序结构。但由于雷达波束通常具有较强的方向性，相控阵雷达尤其如此[2]，因此电子侦察系统难以获得完整的雷达脉冲列，部分脉冲会因为幅度过低而无法被截获[4]。如图1所示，机载侦察接收机可以较完整地截获多功能雷达对它进行照射时的主瓣信号，但在截获雷达照射到其他方向的旁瓣信号时会产生剧烈的幅度波动，并不一定能完整接收。另外，由于侦察过程中会引入参数测量误差，雷达侦察脉冲列在时域上表现为相邻脉冲到达时间差(Differential Time-Of-Arrival,DTOA)序列，而不是脉冲列发射时准确的PRI序列。各DTOA值是对应的脉间PRI值加上测量误差之后的结果。

综合信号截获概率和脉冲到达时间测量误差等因素，得到与图3所示雷达脉冲列相对应的侦察脉冲列示意图，如图5所示。

图3 多功能雷达脉冲列的层次化时序结构Fig.3 Hierarchical temporal structure of multifunctional radar pulse train

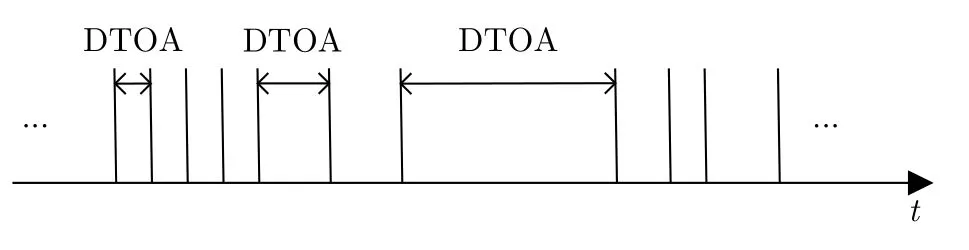
图5 多功能雷达侦察脉冲列示意图Fig.5 Schematic diagram of reconnaissance pulse train of multifunctional radar

该雷达侦察脉冲列可表示为如下字符串形式：

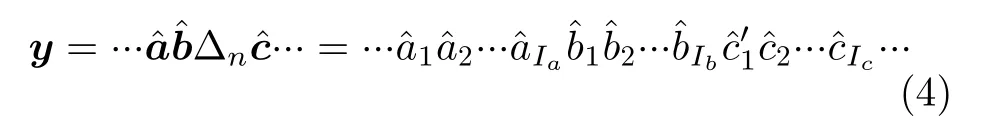
其中，分别是式(2)中对应物理量加上测量误差之后的结果，Δn是由于对特定脉组截获失败而引入的较大脉冲间隔。该脉组的缺失导致相邻脉冲间隔由c1变为综合测量误差之后变对应于图5中标记的第3个DTOA。

对比图5和图3不难发现，在去除了标记雷达脉组的虚线方框之后，雷达侦察脉冲列的时序结构和相邻脉组之间的界线变得十分模糊，雷达信号的层次化模型也不再直观。这一差异源自电子侦察系统对雷达信号模型先验信息的缺失，同时也造成了式(2)和式(4)中对雷达辐射信号序列和雷达侦察信号序列的两种不同形式的表示。两种表示形式中，后一种以脉冲为基本单元，是脉冲列进行语义编码之前的形式，前一种以脉组为基本单元，是语义编码之后的脉冲列表示形式。基于雷达侦察脉冲列提取多功能雷达常用脉组，并反演其层次化信号模型，是本文的研究目标。为方便表述，下文统称式(2)和式(4)中的前后两种表示形式为雷达脉冲列的脉组序列模型和脉冲序列模型。

3 多功能雷达脉冲列描述

在式(4)中，雷达侦察方由于缺少雷达信号时序规律的先验信息，只能分别测量脉冲列中各信号的参数，得到其脉冲序列，而不能获得侦察脉冲列的脉组序列模型。侦测脉冲列中，雷达多种功能脉组的内部时序和它们之间的相互切换过程相互混杂，具有很高的复杂度。相对而言，在式(2)中，雷达发射方可以利用脉组结构先验信息对雷达脉冲列进行压缩编码，压缩之后雷达脉冲列的脉组序列模型具有更加简洁的表达形式和更低的结构复杂度。

在对雷达脉冲列进行压缩编码的过程中，首先将结构性较强且频繁出现的脉冲组合编码为脉组字典集，然后利用该脉组集对冗长的雷达脉冲列进行编码，可以大幅缩减雷达脉冲列的冗余度。对雷达脉冲列的压缩编码过程与雷达脉冲列的层次化建模过程十分吻合。依据奥卡姆剃刀定律[13]，雷达脉冲列的真实层次化模型应当对应于该数据序列的最优压缩编码结构。由于这一压缩编码过程本质上实现了对雷达脉冲列的结构分析，与多功能雷达的实际工作过程密切相关，压缩编码过程也是对雷达脉冲列内容的反演，因此本文将该过程称为对雷达脉冲列的语义编码过程，以区别于常见的语用编码概念[14]。

3.1 语义编码模型及其复杂度度量

数据的压缩编码问题通常包括编码字典构建和基于字典的数据编码两项内容，对多功能雷达侦察脉冲列的编码过程也不例外。雷达侦察脉冲列的编码模型可表述为

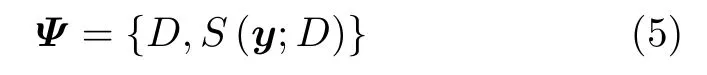
其中，脉组字典集D定义为多功能雷达各功能脉组集合：

式(6)中各变量的含义与式(2)和图3一致，即字典集各元素与雷达不同功能脉组结构相对应；序列S(y;D)是指基于脉组字典集D对雷达脉冲列y编码所得序列，即在式(4)中将y由脉冲列形式·编码为脉组符号序列形式的过程，对应于多功能雷达在不同状态之间的切换过程。需要特别说明的是，由于截获脉冲列中各参数相对于真实雷达信号参数的误差是由侦察测量过程引入的，这些误差是雷达脉冲列层次化模型的外部因素，应当在参数聚类等预处理过程中进行消除，因此本文在原理介绍阶段均不考虑这些误差因素的影响，而在仿真实验部分则会引入这一误差以更好地模拟真实场景。

对雷达侦察脉冲列的压缩编码方式有无穷多种，评价一种编码方式优劣的准则是编码复杂度[9]。对应于式(5)中的编码模型，其复杂度定义为字典复杂度与脉冲列编码复杂度之和：

其中，字典集的编码复杂度取决于其中所包含的PRI数目，定义为

其中，J表示字典集中元素数目，Ij表示第j个字典元素中包含的脉冲数目；c0表示对单个脉冲信号参数的编码长度，如果信号载频、脉宽等参数保持恒定，只考虑脉冲到达时间参数，则单个脉冲的编码长度为c0=log2(DTOAmax/δ)+1，其中δ表示脉冲间隔的量化单元，取决于对DTOA的分辨率要求，DTOAmax表示人为设置的相邻脉冲间隔的最大值，当实际脉冲间隔超过该值时，可将脉冲列分割成两段分别编码，“1”对应于DTOA编码的前缀码元，用于区分编码脉冲列中用真实DTOA值表示的独立脉冲和基于脉组字典集表示的编码脉组。这一编码过程采用了差分编码[14]的原理，编码对象是以相邻脉冲之间的DTOA序列表示的雷达侦察脉冲列，与使用TOA表示的雷达脉冲列相比，DTOA表示方式大幅减少了脉冲序列内部的信息冗余。对脉冲列中各脉冲与前续脉冲的DTOA进行编码，也能实现对一个侦察脉冲序列时序信息的确定性描述。

以下举例对脉冲列编码方式进行说明，并固定各脉冲的载频、脉宽等参数，则雷达脉冲列简化为一个DTOA参数序列。假定脉间DTOA的最大允许值为1 ms，量化单元长度为1 μs，则对单个DTOA的编码长度为对DTOA=23.3 μs的编码结果为00000011000，其中第1个0表示接下来的10位码序列对应于一个脉冲的DTOA编码。如果第1位是1，则表示接下来的码序列对应于字典集D中某元素的符号编码。

基于脉组字典集D对脉冲列y的编码复杂度为

其中，Nj表 示字典集D中第j个元素在脉冲列y中的出现次数，出现次数越多的元素对应的最优编码长度越短，表示依据各脉组在脉冲列中的出现频次进行最优编码时，单个脉组符号对应的平均编码长度[15]；“1”对应于脉组编码时的前缀码元，用于区分编码脉组与独立脉冲；平均编码码元长度乘以脉组总数就得到了对脉冲列中所有脉组编码的总码元数。Nres表示剔除编码脉组后，脉冲列中剩余的未编码脉冲数，这些脉冲需要以独立脉冲形式进行编码，脉冲数乘以单个脉冲编码的码元长度c0，就得到了对剩余脉冲列进行编码的总码元数。脉组编码长度与独立脉冲编码长度相加，就得到了基于字典集D对侦察脉冲列y编码之后，脉冲列的总编码长度。在此基础上，与字典集D的编码复杂度cD相加，就是侦察脉冲列的编码复杂度，对应于式(7)。

这里举一个例子说明对雷达脉冲列的语义编码方式。假定字典集D中包含a,b和c3个脉组，各脉组中包含的脉冲数目分别为Ia=3,Ib=1和Ic=2，它们在雷达脉冲列中分别出现了40次、20次和20次，对单个脉冲的编码长度为11，则对字典集D的编码复杂度为(3+1+2)×11=66，对D中各元素的最优编码方式可设置为{a ⇒0,b ⇒10,c ⇒11}。基于该字典集模型，对式(4)中的脉冲列片段abΔnc(设置Δn=23.3 μs)的编码结果为，利用该编码序列可以唯一地解译出原始雷达脉冲列对应的量化参数序列。尽管对字典集D的编码过程增加了少量的模型复杂度，但由于a,b和c3个脉组在脉冲列中多次出现，脉冲列的压缩编码过程会获得更大幅度的编码效率的增益，因此这种基于字典集的编码方式能够显著缩减对雷达脉冲列的描述复杂度。这种模型复杂度描述方式以信息论为基础，在社交网络领域也有成功应用[16,17]。

3.2 基于模型简洁性原则的脉冲列编码方法

能够用于雷达脉冲列压缩编码的脉组字典集D的形式有无穷多种，其中包括真实的雷达脉冲列时序模型，重建这一模型是本文对脉冲列进行语义编码的目的。当脉组字典集D的内容与多功能雷达脉组结构相吻合时，雷达脉冲列可表示为完全的字符编码形式，其描述复杂度应当是所有模型中最低的。这一推断满足经典的奥卡姆剃刀定律，又称简单性原则，该原则可表述为：如无必要，勿增实体[13]，也就是要用最简洁的模型对观测数据进行充分描述。对于雷达脉冲列编码问题而言，就是应当使用尽可能简单的模型对脉冲列进行充分压缩。

本文就是依据这一模型简洁性原则，寻求对雷达脉冲列进行压缩，以使雷达脉冲列的编码复杂度达到最小，则此时的脉组字典集D即对应于多功能雷达的层次化模型结构。用Dj表示字典集D中的第j个元素，则对脉冲列编码复杂度的最小化寻优过程遵循图6所示的流程，该流程和后续补充说明中，都认为雷达脉冲除到达时间以外的其他参数保持不变，因此脉冲列编码问题简化为DTOA编码问题。

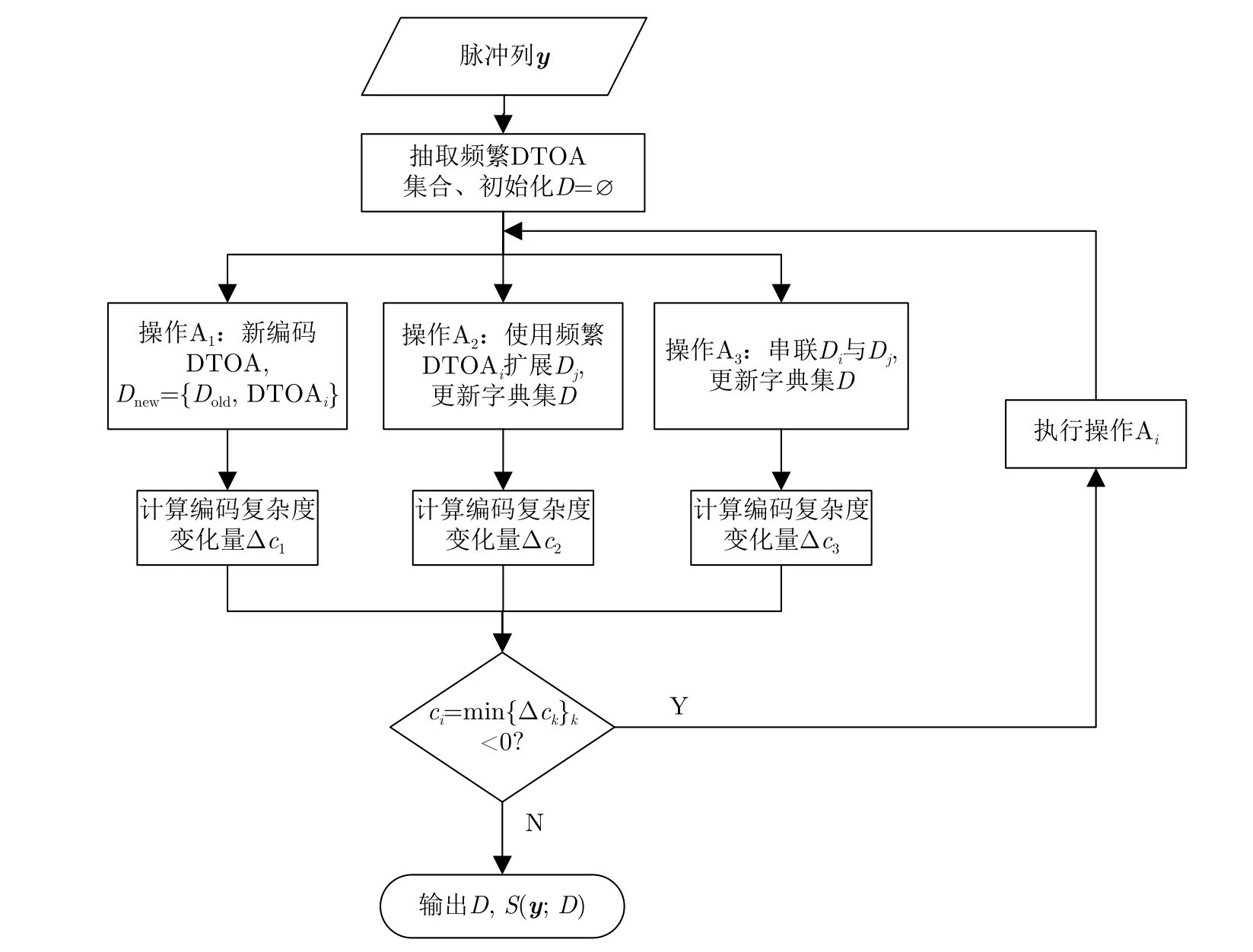
图6 多功能雷达脉冲列编码模型寻优流程Fig.6 Optimization process of the coding model of multifunctional radar pulse train

按照模型寻优的实现过程，对该流程补充说明如下：

(1) 预处理和初始化。对于待编码脉冲列y，首先对脉冲列中频繁出现的脉冲单元(即具有相近的脉冲参数、相邻脉冲间隔的脉冲，在简化模型中对应于脉间DTOA)进行直方图聚类分析[18]，得到频繁脉冲集合，简化形式为DTOA集合

其中，I表示脉冲列中出现次数超过预设门限M0的脉冲数量，每个下标i对应一个频繁项；DTOAi表示第i个频繁项对应的脉冲间隔，通过数值聚类得到，在脉冲列中出现了Mi(Mi ≥M0)次，DTOAi是该类中所有DTOA的平均值；频繁项DTOAi对应脉冲对的首脉冲序号构成集合脉冲序号构成集合之所以预先提取脉冲列中的频繁脉冲单元，用于编码字典集的构建与更新，是因为字典集中的每个DTOA元素都会在字典集编码和脉冲列编码过程中进行重复编码，出现次数较少的DTOA并不会对降低脉冲列的编码复杂度有所贡献。从脉冲列编码问题的物理本质来看，语义编码过程是为了获得脉冲列的脉组结构，仅少量出现的DTOA通常不会与雷达的特定工作模式相对应。对频繁DTOA的聚类分析过程还有利于消除各脉冲TOA测量误差给模型复杂度造成的影响。记录各频繁DTOA的首尾脉冲序号，是为了提高后续脉组扩展和关联等过程的计算效率，避免重复遍历脉冲列[19]。脉组字典集初始化为空集，即D=∅，此时脉冲列的编码复杂度等于对DTOA序列进行直接编码的复杂度。

(2) 脉冲列编码规则与编码复杂度计算。对雷达脉冲列的编码过程是将原始的脉冲列压缩为字符串的过程，伴随着字典集的动态更新，编码过程始终要满足两个基本准则：一是单个脉冲不能被重复编码；二是对脉冲列要尽可能充分编码，即能编码则编码，而不是保留原始脉冲形式，能连续编码就不用分段编码。对于脉冲列的编码复杂度，式(7)已经给出了严格的计算公式，但当脉冲列中脉冲数目较多时，存在对大量脉冲的复杂度不断计算的问题，此时宜采用编码复杂度增量替代绝对的脉冲列复杂度用于模型择优。如果增量为负值，说明该更新过程有利于降低编码复杂度，且负值的绝对值越大，说明对应的更新越有必要。

(3) 操作A1：新编码DTOA，更新字典集Dnew={Dold,DTOAi}。遍历尚未编码的各频繁DTOA项，每次对一个频繁DTOA项进行编码，计算各DTOA项编码对应的模型复杂度变化量，保留复杂度降低幅度最大的一个操作，记录对应的模型复杂度变化量Δc1，用于3类操作之间的择优比较。若最终执行这一操作，则将优选出的DTOAi作为一个新的元素加入字典集，即Dnew={Dold,DTOAi}。

(4) 操作A2：使用频繁DTOAi扩展Dj，更新字典集D。将未编码的各频繁DTOA项用于对字典集D中各元素进行正向或反向扩展，字典集元素的更新会同时改变字典集和脉冲列的编码复杂度，计算模型更新带来的复杂度变化量。记录复杂度降低幅度最大的一种扩展方式，以及对应的模型复杂度变化量Δc2，用于3类操作之间的择优比较。字典集的更新过程分3种情况：如果Dj与DTOAi完全匹配，即Dj对应的每个脉冲片段后面(或前面)都出现了一个间隔为DTOAi的脉冲，则直接将字典集中该元素更新为Dj=[Dj,DTOAi](对应于正向扩展)或Dj=[DTOAi,Dj](对应于反向扩展)；如果Dj与DTOAi完全失配，即Dj对应的每个脉冲片段后面(或前面)都没有出现一个间隔为DTOAi的脉冲，则保持字典集不变；如果Dj与DTOAi部分匹配，即Dj对应的部分脉冲片段后面(或前面)出现了一个间隔为DTOAi的脉冲，则在保留Dj的同时，将Dj=[Dj,DTOAi]或Dj=[DTOAi,Dj]也加入字典集，然后对脉冲列进行重新编码。在频繁DTOA提取和字典集更新过程中，通过记录各DTOA和字典集元素对应的脉冲列序号，就可以通过脉冲序号匹配的方式实现操作A2和A3，而无需返回原始脉冲列进行重新搜索和识别，从而大幅提高计算效率。

(5) 操作A3：串联Di与Dj，更新字典集D。将字典集D中任意两个元素(包括每个元素与其自身)进行串联扩展，计算字典集更新带来的模型复杂度变化量，保留复杂度降低幅度最大的一种串联方式，记录对应的模型复杂度变化量Δc3，用于3类操作之间的择优比较。字典集的更新过程也分为与操作A2中类似的3种情况，这里不再赘述。

(6) 迭代过程与终止准则。在每一轮迭代过程中，通过遍历对字典集D的各种可能的元素新增、元素扩展和元素串联等操作，选取使脉冲列编码复杂度降幅最大的操作Ai，其中若对应的复杂度降幅为正值，则执行最大降幅相应的操作，更新字典集，并对脉冲列进行重新编码；否则，认为字典集的更新已不再能够降低脉冲列的编码复杂度，因此终止迭代过程。

4 多功能雷达工作状态切换模型估计

以脉冲列编码复杂度最小化为准则，采用上一小节的方法，可以获得脉组字典集D，其中各元素对应于多功能雷达执行各种功能时所发射的脉冲序列。在此基础上，对雷达脉冲列进行编码得到符号序列S(y;D)，则该序列与式(2)和式(4)中的第1种脉冲列表示方法具有类似的形式。该表达式中不同脉组之间的切换过程反映了图3所描述的脉冲列的顶层结构，即状态切换矩阵T所控制的多功能雷达脉组切换的概率模型。

对符号序列S(y;D)中表示不同脉组的符号之间的切换规律进行统计，估计得到不同脉组符号之间的切换概率矩阵即为脉冲列顶层结构的概率模型估计值。假定脉冲列编码过程得到了包含3个元素的字典集D，分别表示为a,b和c，对不同脉组之间的切换过程进行计数，得到计数集合N(α →β)(α,β ∈{a,b,c})，其中α →β表示脉组α与β在时序上相互衔接，即脉组α的尾脉冲与脉组β的首脉冲重叠。对计数结果进行归一化处理，得到脉组切换概率矩阵估计值为

这种直接的统计模型估计方法适用于雷达状态数目较少的场景，当雷达状态数目增多时，可以引入可观测算子模型(Observable Operator Model,OOM)[20,21]或隐马尔可夫(Hidden Markov Model,HMM)模型[22,23]等相关方法进行多功能雷达状态切换概率模型的估计，以增强算法稳定性。

5 仿真实验与分析

本部分仿真一个包含2层脉冲结构的多功能雷达模型，并假定脉冲载频、脉宽等参数固定，使用时间信息简化表示雷达脉冲列，以验证本文所提出的雷达脉冲列语义编码原理的可行性，并测试其层次化模型重建性能。

5.1 参数设置

假设多功能雷达共有3种功能，在使用到达时间表示的雷达脉冲列简化模型中，脉组模式可表示为PRI序列形式，3种雷达功能对应的脉组分别为[230 μs,330 μs,430 μs],[300 μs,305 μs,310 μs]和[407 μs,356 μs,285 μs]，雷达在各状态之间的切换过程服从式(11)所给出的概率矩阵。

脉冲到达时刻的TOA测量标准差为0.2 μs。侦察接收机对每个脉组中各脉冲的截获概率同时依赖雷达在该波位处的副瓣电平，因此仿真过程中假设每个脉组内的脉冲要么被全部截获，要么全部丢失。

在频繁DTOA提取过程中，DTOA出现次数的门限设置为5。对脉间DTOA进行量化编码时，取DTOA最大值为DTOAmax=2 ms，量化单元长度为δ=1 μs。

5.2 脉冲列时序模型重建性能验证

首先，假定截获过程中多功能雷达的脉组丢失率为0，侦察脉组数目为300，按照上一小节所设置的参数仿真得到多功能雷达脉冲列，并运用本文所提出的方法对脉冲列进行语义编码分析。在DTOA编码过程中，以出现频度和DTOA取值之商作为择优准则，当不同DTOA出现频度相同时，优先选择DTOA值较小的频繁项进行编码。算法在迭代9次之后终止，每次迭代过程结束之后的脉组字典集D的成分如表1所示，其中蓝色字体标注了当前迭代过程中的编码模型变化情况。

表1 脉冲列迭代编码过程中顺次输出的脉组字典集Tab.1 Sequentially extracted pulse group dictionary set from pulse train during iterative coding process

在对脉冲列进行语义编码的过程中，所提出的算法首先提取了第1种雷达状态对应的脉组，并经过3次迭代从前向后完整重建了该脉组，随后，从后向前重建了第3种状态对应脉组、从前往后重建了第2种状态对应脉组。在完成对3个脉组的提取之后，图6所示流程中的3类字典集更新操作都不能继续降低脉冲列的编码复杂度，迭代过程终止，输出脉组字典集D中的元素作为多功能雷达脉组提取结果，并用于对雷达脉冲列进行编码。

接下来，对脉冲列编码结果中不同脉组之间的切换过程进行统计，得到脉组间切换次数的统计结果如表2所示。

则表2中统计结果对应的估计均方根误差为0.056。通过300次仿真实验结果的综合分析，所有的脉组提取结果都与真实模型相吻合，且统计均方根误差低于0.05。在配置有主频为3.6 GHz的Intel i7-4790处理器、内存为16 GB的计算机上，执行一次脉冲列仿真、语义编码和模型重建的完整过程的平均时间为2.49 s。由于多功能雷达工作模型重建过程通常在离线状态下完成，本文所提出的方法在处理效率上具有较强可用性。

表2 脉组切换次数统计结果Tab.2 Switching number between different pulse groups

最后，改变脉冲列中脉组数目，使之从100到500变化，以测试算法对数据量的需求。每种场景下仿真300次，进行脉组切换矩阵估计精度统计。其结果是，所提出的算法在所有仿真中都能够实现对多功能雷达脉组的准确提取，对脉组状态转移矩阵的估计均方根误差随脉组数目的变化情况如图7所示。可以看出，脉组数目越多，用于统计的脉组切换次数越多，状态转移矩阵的估计精度也越高。当脉组数目超过300时，对状态转移矩阵各元素的估计均方根误差小于0.05，比较准确地反映了多功能雷达的实际工作规律。这一结果说明重建模型能够用于对雷达后续脉组的结构和参数进行预测，从而推断多功能雷达的工作意图。

图7 多功能雷达脉组状态转移矩阵估计精度随脉组数目的变化情况Fig.7 Estimation accuracy of the state transition matrix of multifunction radar pulse group with respect to different number of pulse groups

在实际环境中，多功能雷达极有可能采用捷变载频、PRI等参数，对这类雷达的脉冲列进行编码分析时，数据预处理过程显得更加重要。在预处理过程中，需要有效消除捷变参数造成的脉组多样性影响，对与特定雷达功能相关联的脉冲片段进行充分聚类，以方便进一步的工作模型重建过程。对于载频捷变、脉宽跳变的雷达，本文所提出的基于脉间DTOA的频繁项提取和重频模式分析方法可以有效避免这些捷变参数的干扰，准确分析雷达脉冲列的内在模式；对于PRI抖动的雷达，则要避免对DTOA测量值的直接使用，转而使用隐含在捷变DTOA内部的不变规律。例如，以本小节的仿真实验场景为基础，将多功能雷达脉组的PRI序列设置为抖动模式，原来的脉组内部PRI组合由[230 μs,330 μs,430 μs]等变为[230 μs+δ,330 μs+δ,430 μs+δ]等，其中δ为一个特定范围内的随机数，则在各PRI绝对值变化的同时，它们之间的相对差值保持不变。在这种情况下，测量得到的脉间DTOA集的聚类特性大幅削弱，本文方法将无法直接应用。但是，特定功能雷达脉组内的2阶DTOA(即DTOA序列的差分)仍然具有很好的一致性，以这一不变规律为依据，可以较好地消除捷变PRI参数的影响，并进一步结合本文方法提取捷变参数掩盖下的雷达重频模式。

5.3 数据噪声适应性分析

多功能雷达通常与相控阵天线配合使用，相控阵天线具有很强的方向性和波束指向捷变特性，导致雷达信号在侦察接收机处的增益剧烈变化，侦察接收机对雷达信号的截获情况以脉组为单位跃变，侦察脉冲列中不同功能对应的雷达脉组通常被完整截获或全部丢失。为验证本文方法对雷达脉组丢失所造成的数据噪声的适应能力，在上一小节仿真实验的基础上，设置脉组截获概率为50%，截获脉组数目仍为300，其他参数条件不变，使用本文方法对残缺脉冲列进行语义编码，得到编码字典集对应的多功能雷达脉组提取结果如表3所示。

与真实信号模型相比，表3中除了多功能雷达3种状态对应的脉组之外，还额外包含了3个脉组，分别是雷达各脉组缺失最后一个PRI值之后的非完整形态。这种情况是由后续脉组未被截获造成的。当多功能雷达在当前状态下发射完最后一个脉冲，并预留了一个回波接收时窗之后，由于后续脉组未被截获，当前脉组的最后一个PRI在截获脉冲列中并没有显现出来，该脉组的模式表现为一个残缺形态。并且，表3中3种完整形态脉组的数目之和与非完整形态脉组的数目之和基本一致，与50%漏脉组率的设置是吻合的。

表3 漏脉组率为50%条件下的脉组提取结果Tab.3 Extracted pulse groups from a pulse train with 50% pulse missing

为了更加充分地验证本文方法对漏脉组率的适应能力，在表3对应实验的基础上，将多功能雷达脉冲列的漏脉组率从0逐步增大至80%，每种场景下进行100次仿真实验。在每次实验中，如果重建结果中仅包含真实的雷达脉组，以及由漏脉组导致的最后一个PRI值缺失的脉组(与表3类似)，则认为重建结果正确。基于这一判决准则，得到不同漏脉组率情况下多功能雷达脉组重建正确率如图8所示。

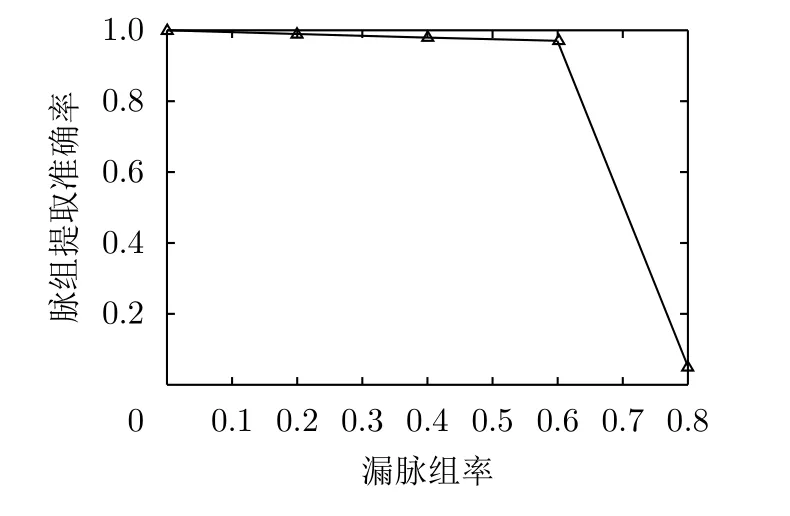
图8 多功能雷达脉组重建正确率随漏脉组率的变化情况Fig.8 Probability of correct pulse group reconstruction with respect to different missing ratios of pulse groups

图8的结果表明，本文方法对漏脉组具有较强的适应能力，在漏脉组率高达60%时，脉组重构正确率仍然达到95%以上。随着漏脉组率进一步增大，雷达不同功能对应的完整脉组出现的次数越来越少，从观测得到的雷达脉冲列中难以再获得完整的脉组结构，导致脉组重构结果容易出现错误，脉组重建正确率大幅下降。

对于脉组大量丢失所引起的编码字典集提取不准确的问题，可以结合各脉组在脉冲列中的上下文和相似脉组之间的关联性，对本文方法所得脉组重建结果进行修正，从而加以解决。还可以通过分析各完整脉组的持续时长与脉冲列中非相邻脉组之间DTOA的对应关系，对缺失的脉冲片段进行补齐，以增加用于雷达状态切换矩阵估计环节的数据量，提高状态切换矩阵的估计精度。

6 结束语

本文通过深入分析多功能雷达脉冲列的层次化结构的形成机理，提出了对多功能雷达进行工作模式分步重建的方法。首先引入信息论和压缩编码理论，定义了多功能雷达脉冲列的编码复杂度，随后以模型简洁性原则为依据提出了编码策略优化方法，最优编码策略对应的编码字典集中包含了雷达的不同功能脉组，最后基于脉组字典集对雷达脉冲列进行编码，从编码字符串中可以统计雷达状态切换概率矩阵，从而实现了对多功能雷达脉冲列时序模型的完整重建。仿真结果表明，本文所提出的方法能够准确揭示多功能雷达脉冲列的内部结构和雷达工作规律，截获脉冲数越多，重建模型越准确。通过对本文方法进行修正和扩展，可以适应漏脉冲等各种数据噪声环境。

本文以具有2层脉冲列结构的多功能雷达为例，并将其顶层脉组结构建模为1阶马尔可夫过程，进行了雷达脉冲列语义编码与功能重建的原理分析、算法介绍和仿真验证，研究成果的实用性和局限性可概括为两个方面。首先，该成果能够较好地直接应用于三坐标和早期相控阵等体制的多功能雷达，这些雷达具有比较确定和简单的工作状态切换规则，其信号模型与本文模型较为吻合。其次，对于具有多层(≥3)脉冲列结构的多功能雷达，则需要对本文方法进行相应的扩展，修正脉冲列的语义编码过程以实现对多层脉组结构的提取和描述，然后基于脉冲列的编码结果估计状态切换概率矩阵；更进一步地，对于具有可变阶数的状态转移模型和多子阵同时工作的相控阵雷达等先进目标，则可以将本文模型重建结果应用于分析和剔除混杂脉冲列中的由简单体制雷达产生的背景信号，然后以提纯之后的多功能雷达数据为基础，对本文提出的脉冲列语义编码原理进行深化研究，用于重建复杂体制多功能雷达的工作模型。