基于熵权法的艺术家音乐影响力评价模型

万昭龙 芮晓芳 王 繁

（长安大学运输工程学院，陕西 西安 710064）

一、问题重述

音乐从一开始就是人类社会的一部分，是文化遗产的重要组成部分。为了理解音乐在人类集体经验中所扮演的角色，要求我们开发一种量化音乐进化的方法。当艺术家创作一段新的音乐时，有许多因素会影响他们，包括他们天生的创造力，当前的社会或政治事件，使用新乐器或工具，或其他个人经历等，通过量化，我们旨在了解和衡量之前制作的音乐对新音乐和音乐艺术家的影响。

问题一：创建音乐影响力的（多个）定向网络，其中影响者连接到追随者。开发参数来捕捉这个网络，通过创建定向影响者网络的子网络来探索音乐影响力的子集。并描述此子网，在这个子网络中揭示了什么？

问题二：使用音乐特征的汇总数据集（具有艺术家和年份）来开发音乐相似性度量模型。

二、模型假设

第一，同一个音乐家所写歌曲之间的相似度会较高。

第二，这个音乐家与受其影响者歌曲的相似度也会较高。

第三，这个音乐家与不受其影响者歌曲的相似度较低。

三、符号说明

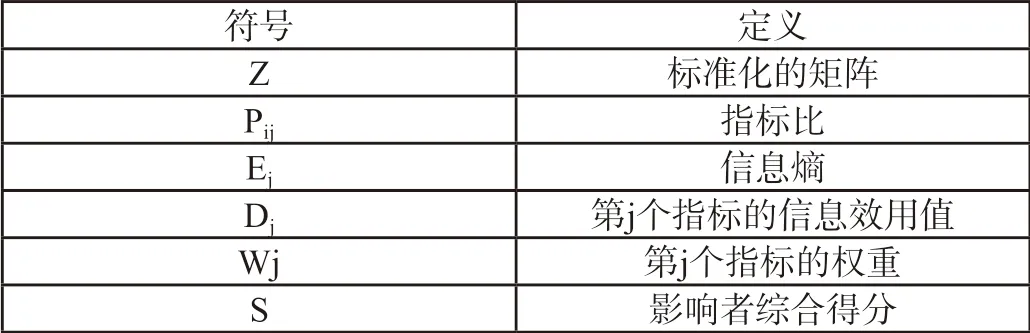
表1 符号说明

四、模型的建立与求解

1. 数据的预处理

为了提高数据挖掘的质量，并为后续的模型建立提高数据支撑，数据预处理是必不可少的。数据预处理主要包括异常值和冗余数据的处理。首先，考虑到异常值的处理，本文使用python删除了Impact-Data数据集中的影响者名称和追随者名称中的异常名称（包括特殊符号），如表2所示，例如B9062：Édith Piaf。排除异常值后，数据量从原始的42770更改为41494。

表2 数据异常值的处理

2.艺术家定向网络的建立

为了建立影响者与追随者的连接图，本文利用python工具箱中的networks工具建立了定向网络图，网络图显示了一组实体之间的互联，每个实体由一个或者多个节点表示，彰显出节点间的映射关系。如图2所示，对2010年开始艺术生涯的艺术家建立定向网络，反映在此期间，音乐家之间的相互关系，此图中Frank Ocean， Flume， Alt-J， The Weeknd等人都影响了两个艺术家，而其他艺术家不是影响一个艺术家就是被一个艺术家所影响，可以推测Frank Ocean，Flume， Alt-J， The Weeknd的影响力和地位较高。图中箭头指向的是被影响的艺术家，箭头的起点处是发挥影响的艺术家。由图2还可知，虽然在2010年开始艺术生涯的艺术家人数不多，但是他们之间还是有着较为复杂和密切的关系。研究此期间艺术家之间的关系，探寻期间艺术家的影响力，对于提取数据、推广我们的影响力评价模型有着至关重要的作用。

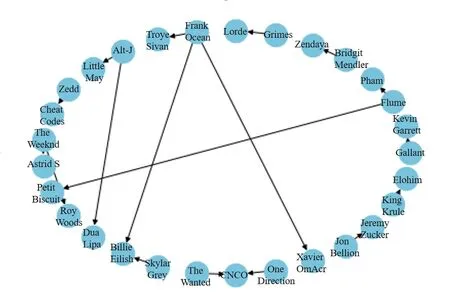
图2 艺术家之间的定向网络图

3.基于熵权法的艺术家音乐影响力评价模型

3.1 熵权法基本原理

熵权法是一种客观赋权方法，在使用过程中，熵权法根据各指标的变异程度，利用信息熵计算各指标的熵权，再利用熵权对各指标的权重进行修正，从而得出较为客观的指标权重的方法，最后计算出得分，通过对得分的排序，确定影响力的大小。熵权法模型步骤如下。

第一，第i个影响者的第j个指标的比重。

第二，第j个指标的信息熵和信息效用值。

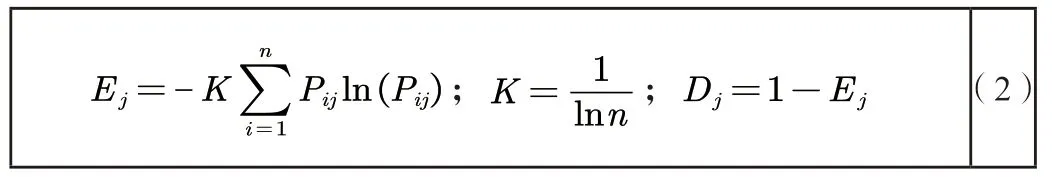
第三，计算第j个指标的权重。

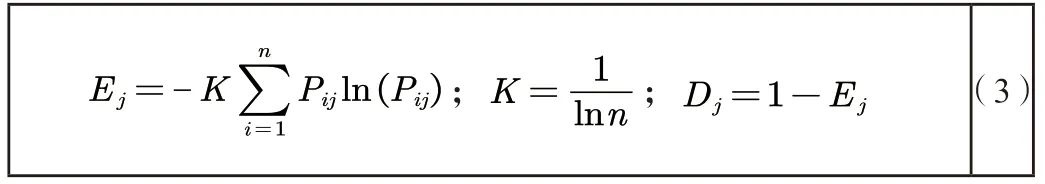
第四，指标加权计算得分。

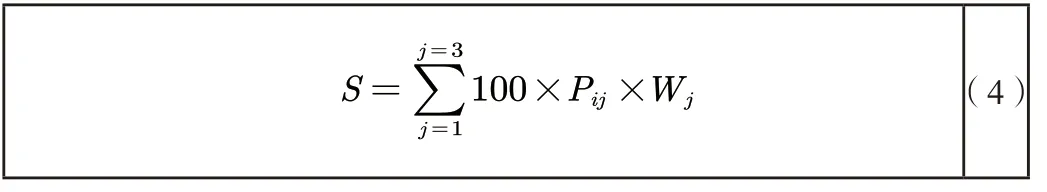
3.2 评价指标的构建

对于音乐影响力评价指标，考虑到题目要求与所给数据，只能从influence_data数据集中提取指标。基于统计学理论和相关文献的查阅发现，影响力的确定涉及相对性与绝对性的观点，影响人的追随者越多，相应的艺术家影响力就越大；如果他所在领域的艺术家本身很少，但他影响了绝大部分人，也可以认为他的影响力较大。例如blues流派有1000人，一个影响者影响该领域的300人，但是另外一个影响者属于jazz流派，他影响50个人且他的领域里面只有60人，说明在该领域这个人也有统治般的影响力。

因此，在确定指标时，相应地权衡各领域人数，为此，本文把艺术家的影响人数和所在领域年份总人数作为评价指标。最后，结合指标选取与结合的原则，经过筛选后，确定评价指标为跟随者数量、跟随者派别个数、影响者派别总数。如表3所示，选取和统计了2010年开始艺术生涯的艺术家的评价指标数据。

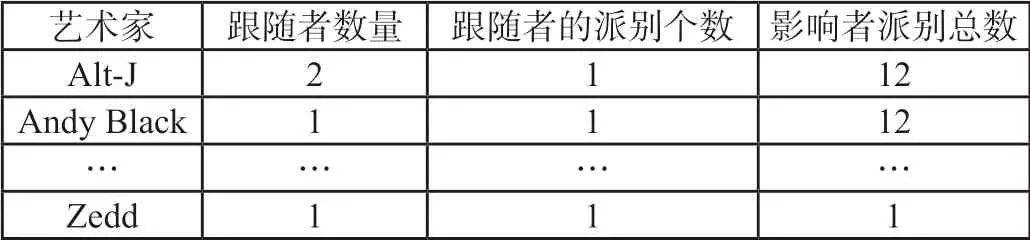
表3 评价指标统计

3.3 数据标准化处理

假设有n个要评价的对象，m个评价指标构成的正向化矩阵为X，对X进行标准化的矩阵记为Z。

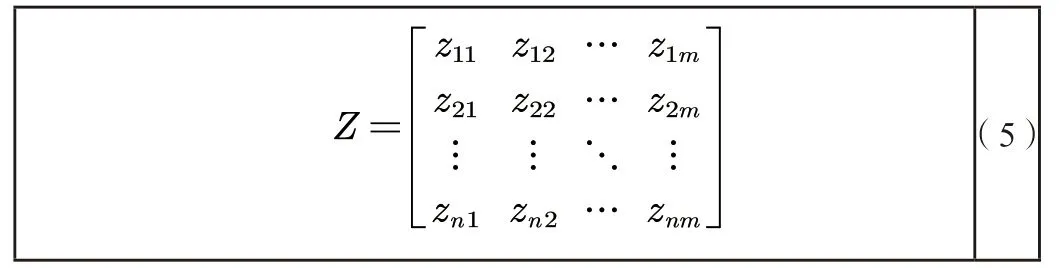
3.4 结果求解与分析

由于指标数量较少且计算相对简便，利用excel进行求解。以2010年开始音乐生涯的艺术家为例，各指标权重和影响力综合评分结果见表4和表5。由表4可知，在三个因素当中，影响者派别总数的权重最大，表明其在评价影响力时更为重要，即一个人影响力的大小，更多地取决于影响者派别总数，由表5可知，2010年开始音乐生涯的艺术家，名为Flume的艺术家音乐影响力最大。

表4 各要素计算结果

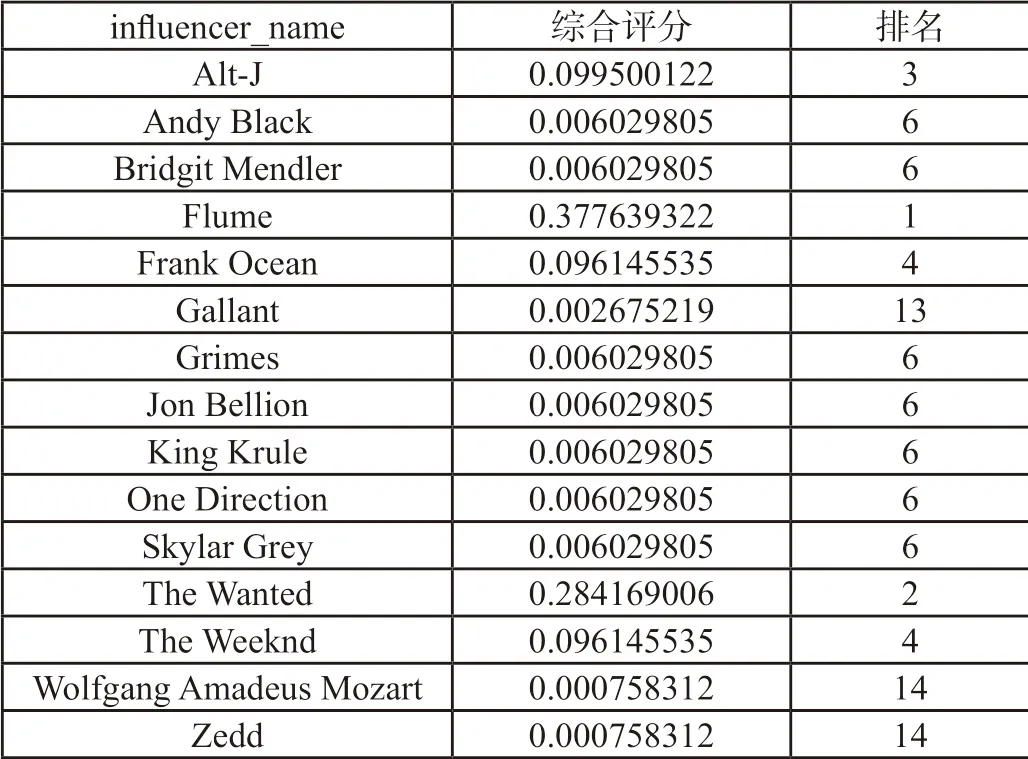
表5 影响力综合评分结果

4.音乐相似度模型指标的确定

根据full-music-data发现，评价音乐相似度的指标较多，本文从听众的角度出发，以popularity为参照，利用JMP软件，对指标的相关性进行分析，求得各个指标与popularity相关性，如表6所示。

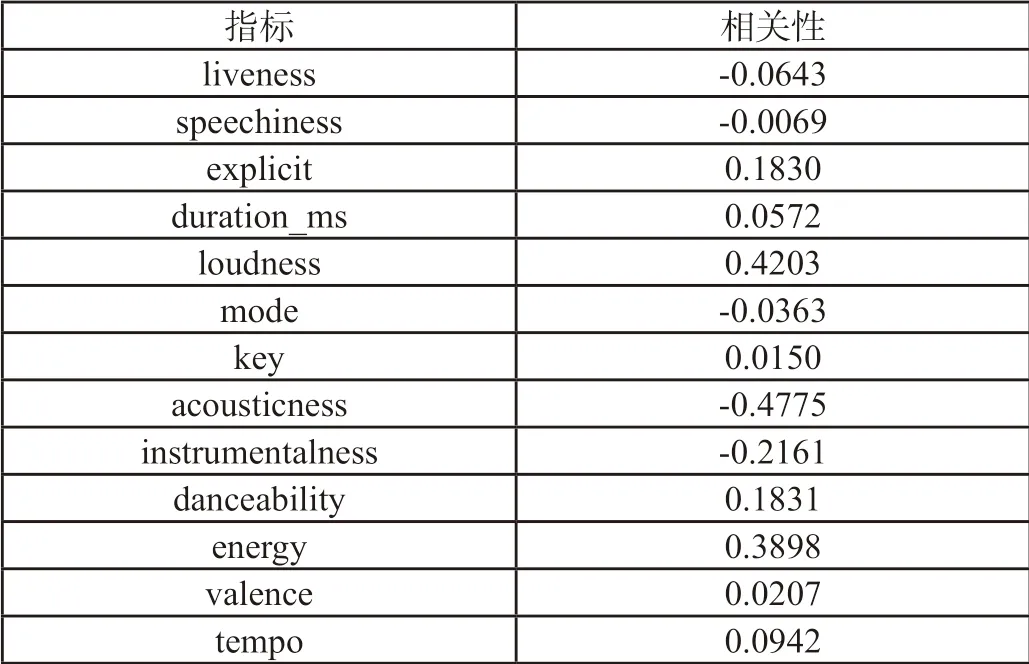
表6 指标相关系数

当相关性系数绝对值小于0.1时，相关性系数太低。所以去掉相关性绝对值小于0.1的指标。由表6可知，explicit、loudness、acousticness、instrumentalness、danceability、energy和tempo作为音乐相似度模型的评价指标。

5. 音乐间的相似度模型

5.1 音乐相似度的探寻思路

结合上面所建立的影响力模型，从三个角度探寻音乐之间的相似度，首先，从同一艺术家的歌曲出发，探寻这个艺术家所写歌曲的相似度。其次，从这个艺术家和受这个艺术家影响的人出发，探寻这个艺术家和其被影响者歌曲之间的相似度。最后，从这个艺术家和没受这个艺术家影响的人出发，探寻这个艺术家和没受其影响者歌曲之间的相似度。

5.2 模型的建立及验证

5.2.1 模型指标的定义

Z为歌曲相似度，Z={A1，A2，...Am}，Ai（i=1,2,…,m）为选定的歌曲，Ai={xi1，xi2，...，xi7}其中xi1，xi2，...xi7分别为 指 标explicit、loudness、acousticness、instrumentalness、danceability、energy和tempo。

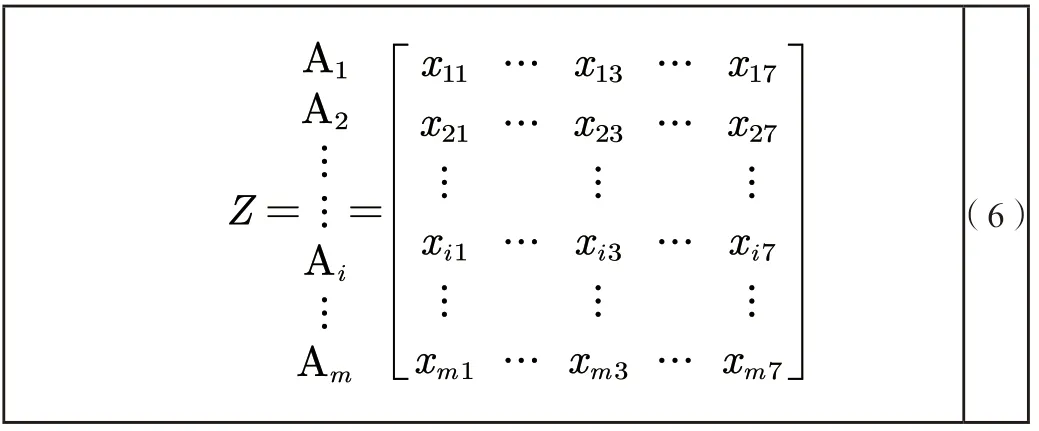
5.2.2 建立初始化矩阵

将m个选定的歌曲对象和n个歌曲指标，建立正向化的初始评价矩阵Z。

5.2.3 数据无量纲化处理

为了消除各个指标之间的量纲带来的影响，需要对数据进行无量纲化处理，本文利用最小-最大标准化进行数据的处理。

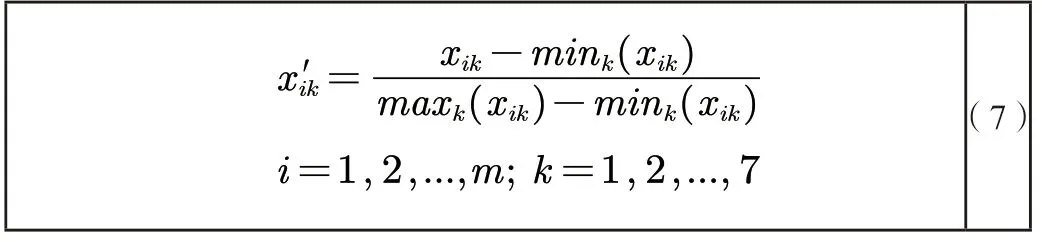
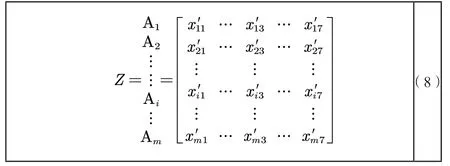
归一化后的矩阵可表示为

5.2.4 相似度的求解

求解歌曲之间的相似度，利用皮尔逊系数，计算公式如下。

根据影响力模型，选中Flume这个艺术家对其进行分析，选取Flume这个艺术家的8首歌曲进行分析，接着按照上述音乐相似度模型的求解，得出歌曲间的皮尔逊系数，Flume各个歌曲与歌曲Ezra的皮尔逊系数如表7所示，Flume与其影响者歌曲之间的皮尔逊系数如表8所示，歌曲家Flume的歌曲Ezra与不受其影响的歌曲之间的皮尔逊系数如表9所示。

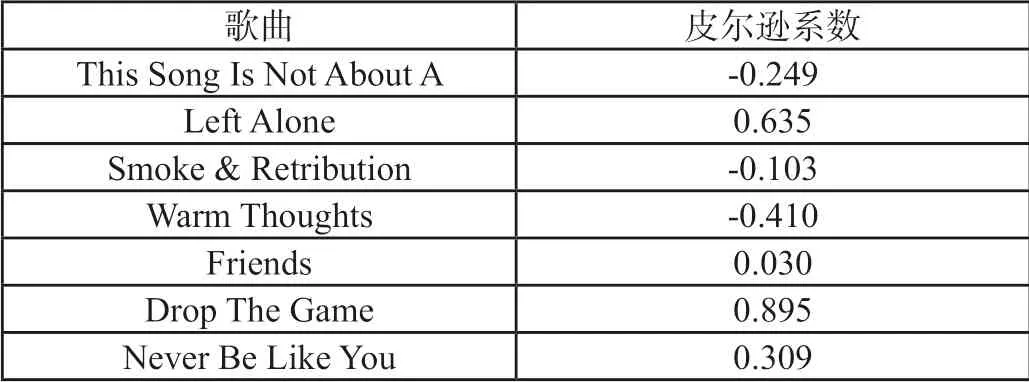
表7 Flume各个歌曲与歌曲Ezra的皮尔逊系数

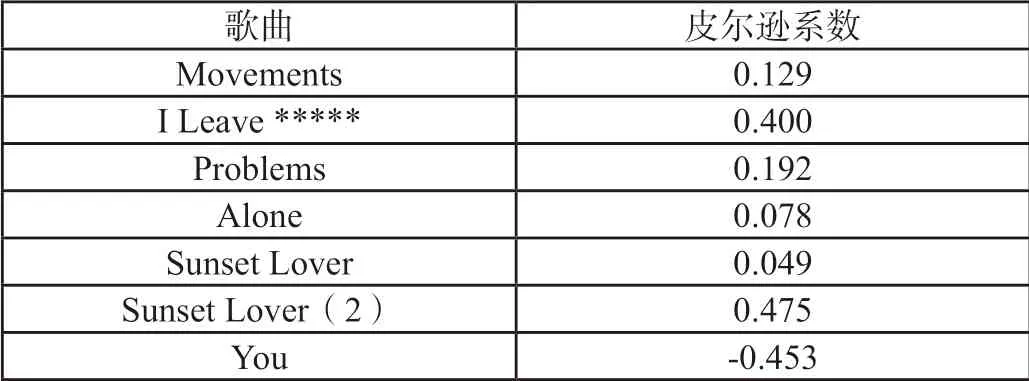
表8 Flume与其影响者歌曲之间的皮尔逊系数

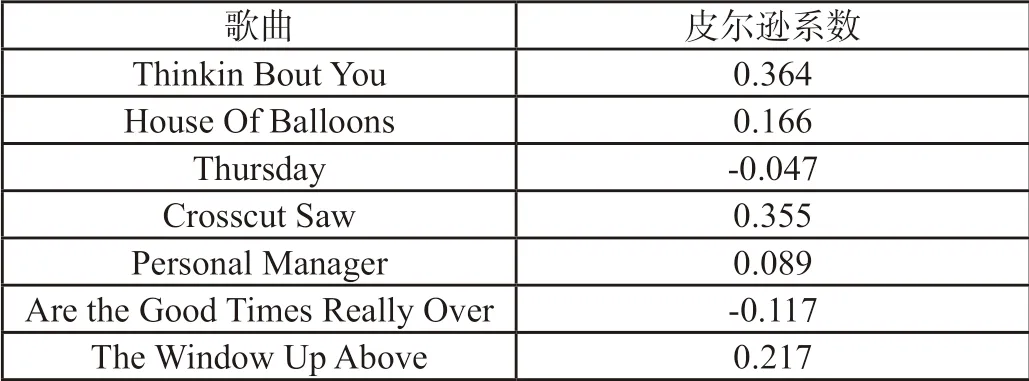
表9 Flume与不受其影响的歌曲之间的皮尔逊系数

5.3 数据分析

从表7至表9中得出，对于Flume这个音乐家，其创作的作品中，存在与其创作的音乐Ezra具有强相关的歌曲，但是有些歌曲与音乐Ezra相关度不是很高，符合实际情况。在实际生活中，同一个音乐人创作歌曲会有很多同一类型的歌曲，其旋律歌词都比较类似，也会存在音乐创作人另辟蹊径，创作出与自己平时创作歌曲风格截然不同的情形。

对于受Flume这个音乐家影响的歌曲家，他们创作的一些歌曲会跟Flume创作的歌曲Ezra有较大的相关度，有一些相关度较低，其也较为契合实际，一些歌曲家在创作时，在旋律歌词等较多的借鉴其影响者的创作风格，而有些歌曲家只是在其创作灵感上借鉴了其影响者。

至于不受其影响的歌曲家创作的作品，因为一些音乐流派其旋律等风格相似，从而也会导致歌曲之间也会有些许相似，但是其相似的比值不会很大。

从上面得到的数据和分析中，验证了之前的假设，从而进一步说明了本文所建立的音乐相似度模型的正确性。

五、总结与评价

通常来说一个艺术家音乐影响的人数越多其影响力越大，然而通过基于熵权法的音乐影响力模型分析发现，艺术家的音乐影响力更多取决于艺术家所在流派中受其影响人数的比例。艺术家与受其影响的艺术家之家的歌曲相似度较大，由于流派之间旋律等因素的相似，也会造成不同流派之间的歌曲相似较高。

本文所建立的评价模型，可以将错综复杂的艺术家之间的关系，进行简便可靠又较为客观的分析与评价，从而得到艺术家影响力的大小，以及艺术家之间歌曲的相似程度。

在未来，我们将模型进一步优化，将艺术家之间的关系进行更多层次的评价，对于艺术家影响力的评价会有一个更加客观和可靠的结果；将音乐进行指标的量化，把抽象的音乐旋律变成可视的指标数据，进而利用量化的指标出发，探寻音乐的相似度，对于探究音乐之间的相似度会有更高的准确性。这种探究思路，对于音乐界艺术家的评价和音乐之间的相似度评价具有极高的可操作性和客观性，可以为量化音乐、分析音乐影响力提供一定的思路，并可用于音乐特征提取、音乐推荐系统中。