火电机组锅炉烟气含氧量预测

耿铭垚， 胡 锐， 李 凌

（1. 上海理工大学 能源与动力工程学院，上海 200093；2. 杭州华源前线能源设备有限公司，杭州 311106）

火电厂经济运行主要是锅炉经济运行，即提高锅炉的热效率。目前，国内火电机组锅炉热效率一般可以达到92%左右，在锅炉的各项热损失中排烟损失和未完全燃烧损失是占比最大的两项，分别在4%和2%左右，而影响这两项损失的主要因素就是烟气含氧量。在优化锅炉燃烧系统时，若要更好地了解锅炉的运行状态，则需要准确测量锅炉的重要运行参数。因此，烟气含氧量是反映锅炉燃烧状况的一个重要参数[1]，烟气含氧量的及时、准确测量变得非常重要。目前，我国火电厂大多使用氧化锆传感器和磁式氧气传感器对氧气进行测量，但这些方法普遍存在滞后大、精度低、硬件成本高、稳定性差等缺点，难以满足电厂长期实时监控的要求[2]。近年来，随着机器学习和深度学习技术的发展，神经网络被广泛应用于工业过程监控。在烟气含氧量方面，国内已有学者提出将反馈BP（back propagation）神经网络应用到烟气含氧量预测中，并取得了理想的结果[3]。但单一的BP网络模型收敛速度慢，容易陷入局部最优。而遗传算法GA（genetic algorithm）能够求出优化问题的全局最优解，且算法独立于求解域。使用遗传算法对BP神经网络的初始权值和阈值进行优化，相比于随机的初始权值和阈值将会有效提高BP神经网络的收敛速度和准确性。本文以某350 MW超临界中间再热间接空冷抽汽凝汽式机组为例，提出了一种GA-BP模型用于预测电厂的烟气含氧量。

1 BP神经网络及遗传算法

BP神经网络是一种反馈神经网络，它的主要特点是信号向前传播，而误差却是反向传播，其模型结构如图1所示。图中：Xn为BP神经网络的第n个输入变量；Oj为BP神经网络的第j个输出结果。BP神经网络的传播过程根据其特点主要分为两个阶段：第一阶段是输入信号向前传播，从输入层到隐含层，最后到达输出层；第二阶段是误差的反向传播，根据误差首先调节输出层和隐含层间的权值和阈值，之后调节隐含层到输入层间的权值和阈值[4]。上述误差反向传播算法作为网络的基本训练算法，存在着收敛速度慢、容易陷入局部最优等问题。为了克服神经网络的这些缺点，研究人员提出了许多改进的算法，例如自适应学习率算法、粒子群算法[5]、GA算法等[6]。

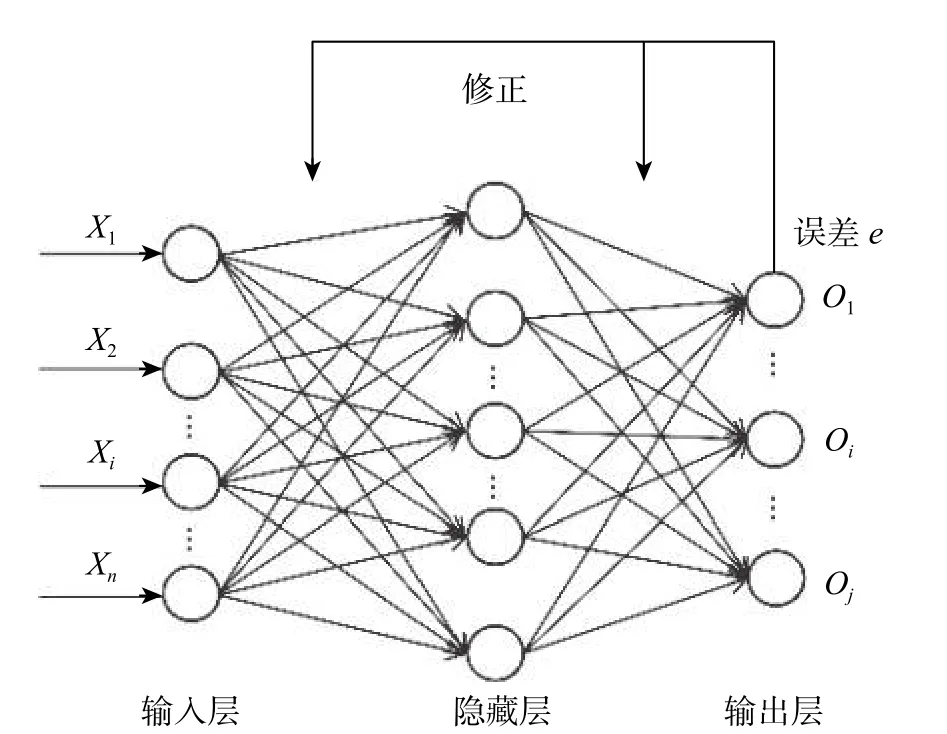
图1 BP神经网络模型的结构Fig.1 Structure of BP neural network model

遗传算法一般从两个方面对神经网络进行优化：一方面利用遗传算法确定BP神经网络的结构，包括神经网络的层数、每一层的节点数；另一方面利用遗传算法优化神经网络的初始权值和阈值[7]。本文模型的目的是为了提高神经网络的收敛速度和预测结果的准确性，所以选择第二种优化方法，即通过遗传算法优化后的权值和阈值使神经网络的输出值与目标值间的误差平方和最小。其优化过程如下：a.初始权值和阈值的编码，本模型使用二进制编码；b.解码，求解个体适应度；c.判断是否满足条件，满足条件则输出权值和阈值，不满足条件则进行下一步；d.对输出的权值和阈值编码进行选择、交叉、变异；e.重复第二步直到输出权值和阈值；f.将输出的权值和阈值输入到神经网络里；g.计算隐含层、输出层的输出值；h.计算输出层结果与实际值的误差；i.判断误差是否满足要求，满足要求则输出结果，否则进行下一步；j.计算每个误差的梯度，更新所有的权值和阈值，重复步骤g直到步骤i满足要求为止。遗传算法优化BP神经网络的流程如图2所示。

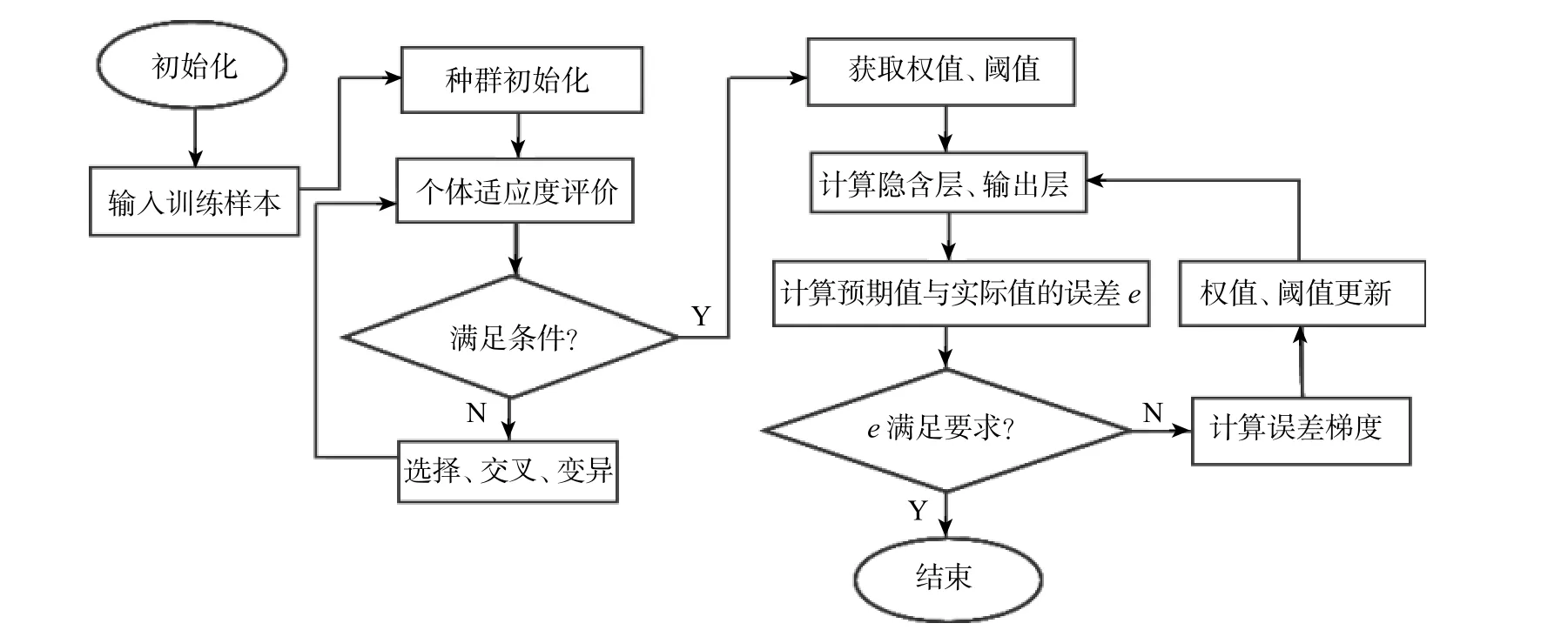
图2 遗传算法优化神经网络流程图Fig.2 Flow chart of BP neural network optimized by genetic algorithm

2 数据预处理及辅助参数选取

在选择辅助变量时结合电厂的机理分析初步选取了排烟温度、给水流量、机组负荷、总风量、给煤量、主蒸汽压力、一抽温度、再热压力作为辅助参数，烟气含氧量作为主元参数。

火电厂的生产环境复杂，存在各种磁场、电场，使得传感器测得的原始数据容易受到干扰，不可避免产生误差[8]。没有经过处理的数据用来直接建模会影响模型的精度，因此，在建模前必须进行数据的预处理。数据的误差类型主要分为粗大误差和随机误差。本文采用拉依达法则去除粗大误差。先假设一组监测数据只含有随机误差，对其进行计算得到标准偏差，按照一定的概率确定某个区间，认为超出这个区间的误差就不属于随机误差而是粗大误差。在正态分布中σ代表标准差，μ代表平均值，可以认为变量的取值全部集中在（μ-3σ，μ+3σ）区间内，超出这个范围的应予以剔除[9]。消除随机误差通常采用数字滤波方法，本文采用五点三次平滑滤波对数据进行平滑处理[10]。以机组负荷为例，其原始数据如图3所示，图4为去除误差后的数据。

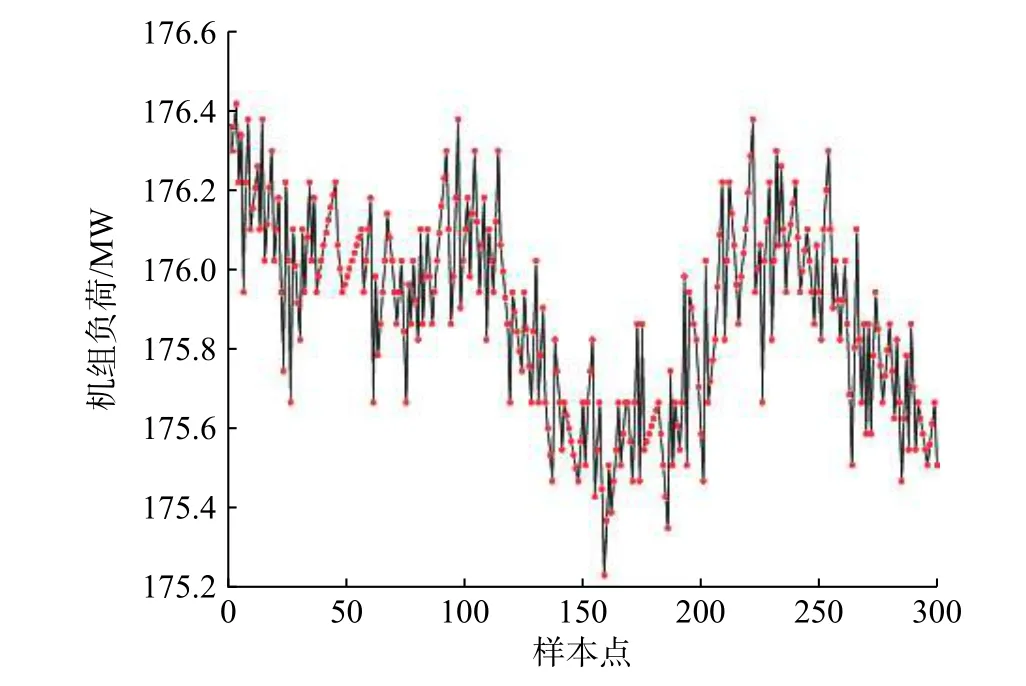
图3 现场运行原始数据Fig. 3 On-site operation raw data

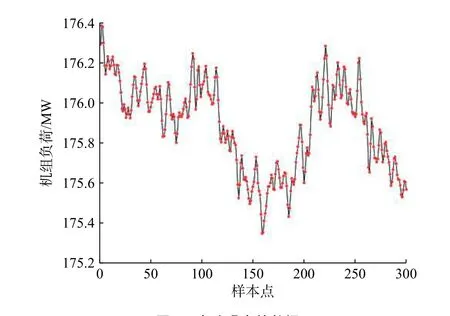
图4 去除噪音的数据Fig. 4 Noise-removed data

在训练前必须将数据进行归一化处理，以减小计算量和避免误差扩大。归一化数据如图5所示。初步选取的辅助变量可能存在某种相关性且维度较高，在建模前运用偏最小二乘算法对初步选取的辅助变量进行主元分析。

图5 归一化后的数据Fig. 5 Normalized data

偏最小二乘法是基于因子分析的多变量校正方法，其数学基础为主成分分析[11]。它综合了多元线性回归和典型相关分析的基本功能。当数据量小，甚至比变量维数还小，而相关性又比较大时，这个方法要优于主成分回归，它相对于主成分回归更进了一步。辅助变量与主元的关系通过各自的回归系数表达出来，回归系数的绝对值大小代表辅助变量对主元影响的大小。用偏最小二乘算法对初步选取的辅助变量和烟气含氧量进行回归分析，得到回归系数分别为：K1=0.232 1，K2=-0.154 3，K3=0.174 2，K4=0.336 4，K5=-0.442 1，K6=-0.132 1，K7=0.011 6，K8=-0.001 7。

对各系数进行排序，根据系数大小确定输入量对输出的贡献率，如表1所示。

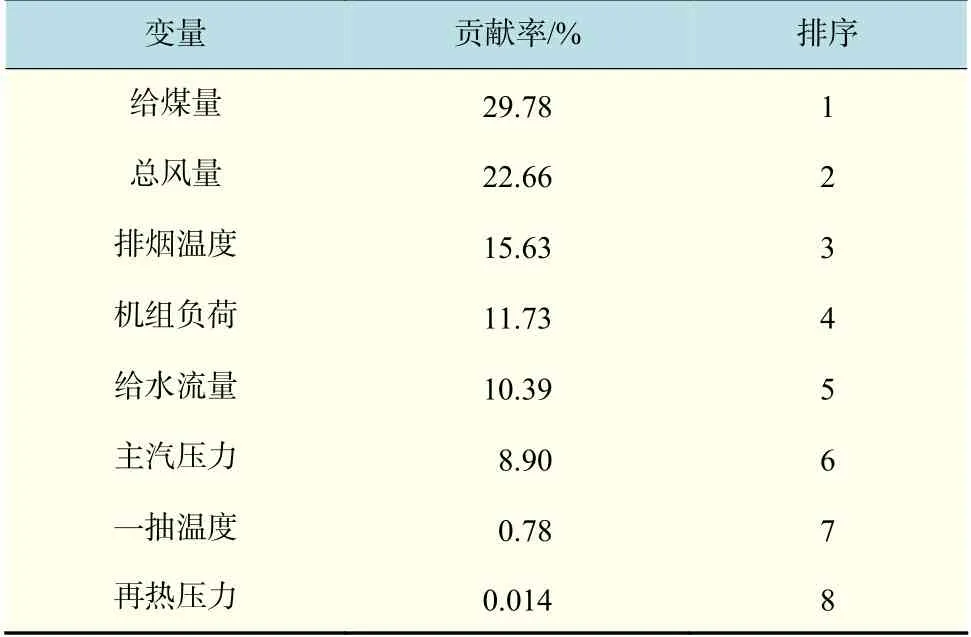
表1 输入量对输出的贡献率Tab.1 Contribution rate of input to output

将贡献率低于1%的变量舍去，得到最终辅助变量分别为排烟温度、给水流量、机组负荷、总风量、给煤量、主蒸汽压力。表2给出了辅助变量的部分运行数据。得到的烟气含氧量估计值与实测值的误差如图6所示，最大的偏差在-9%～5%之间。

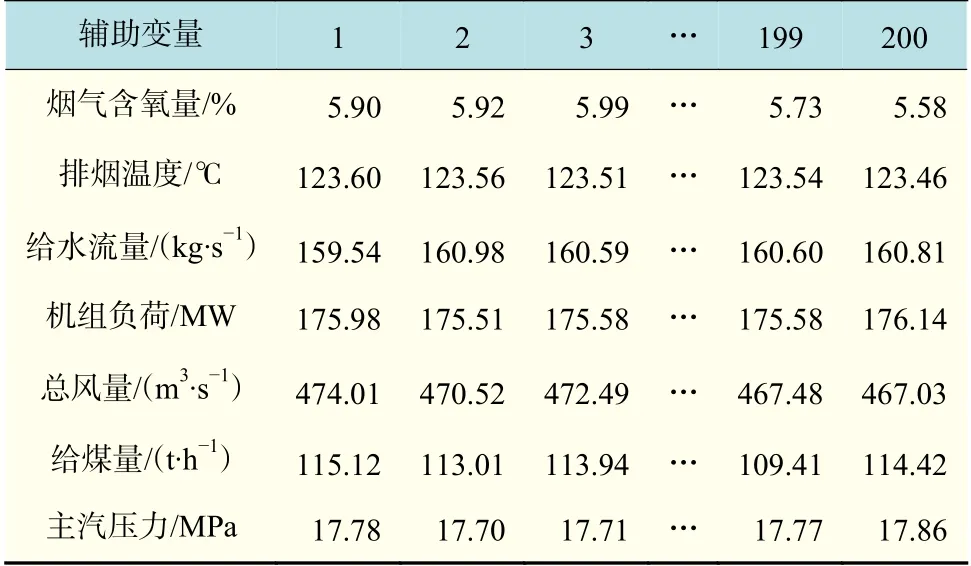
表2 辅助变量部分运行数据Tab.2 Auxiliary variable part of operating data

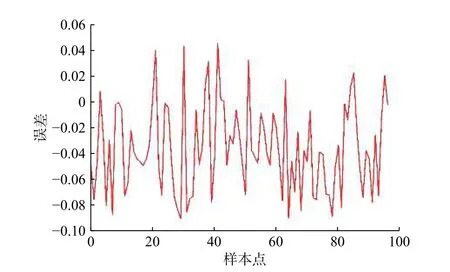
图6 偏最小二次回归误差分析Fig.6 Error analysis of partial minimum quadratic regression

3 烟气含氧量建模

建立的神经网络为含有一个隐含层的反馈神经网络[12]，输入层有6个辅助变量：排烟温度、给水流量、机组负荷、总风量、给煤量、主蒸汽压力。隐含层节点个数为13，此节点个数由试凑法得出[13]，先设置较少的隐含层节点作为初始值，然后逐步增加隐含层节点数，最后选择误差最小时所对应的隐含层节点数。当训练精度达到0.001时的网络迭代次数和隐含层节点数的关系如表3所示。

表3 迭代次数和隐含层节点数的关系Tab.3 Relationship between the number of iterations and the number of hidden layer nodes

输出层为烟气含氧量。通过训练对比将期望误差设置为0.001。隐含层的神经元函数采用Sigmod特征函数[14]，即

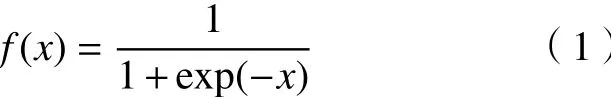
输出层的神经元函数采用Pureline特征函数，即

神经网络的误差函数采用均方误差MSE[15]，即

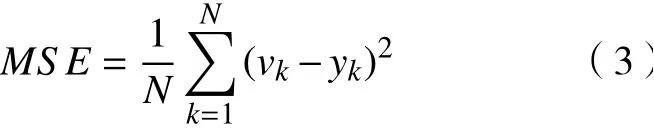
式中：yk为第k个预测值；vk为第k个实际值；N为预测数据的数量。

使用遗传算法对BP神经网络的91个权值14个阈值共105个参数进行寻优。遗传算法的遗传代数设为100，种群个体数目为20，采用轮盘赌选择方法确定个体的生存和淘汰。交叉概率pc=0.5，变异概率pm=1/91，取神经网络误差平方和作为适应度函数，种群最优个体目标函数值变化如图7所示。

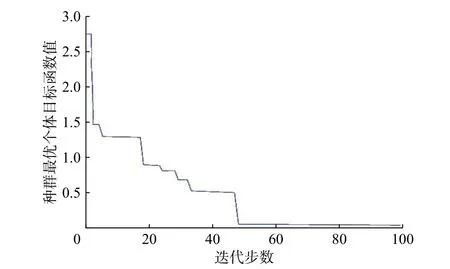
图7 种群迭代过程中的最优目标函数值Fig.7 Optimal objective function value during population iteration

最终得到的最优个体适应度为0.22，对应的进化代数为48，且48代之后种群最优个体目标函数值将不再发生变化。由此可判断此时已达到最优个体目标函数值。取150组预处理过的数据用于训练网络模型，当达到期望误差时结束训练。图8为模型训练过程的误差变化情况。

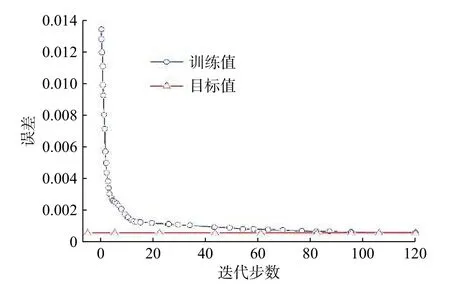
图8 GA- BP模型训练图Fig.8 GA-BP model training diagram

4 模型验证与分析

选取50组未经训练的数据检验模型精度，将预测结果与电厂实际数据进行对比分析，如图9所示。

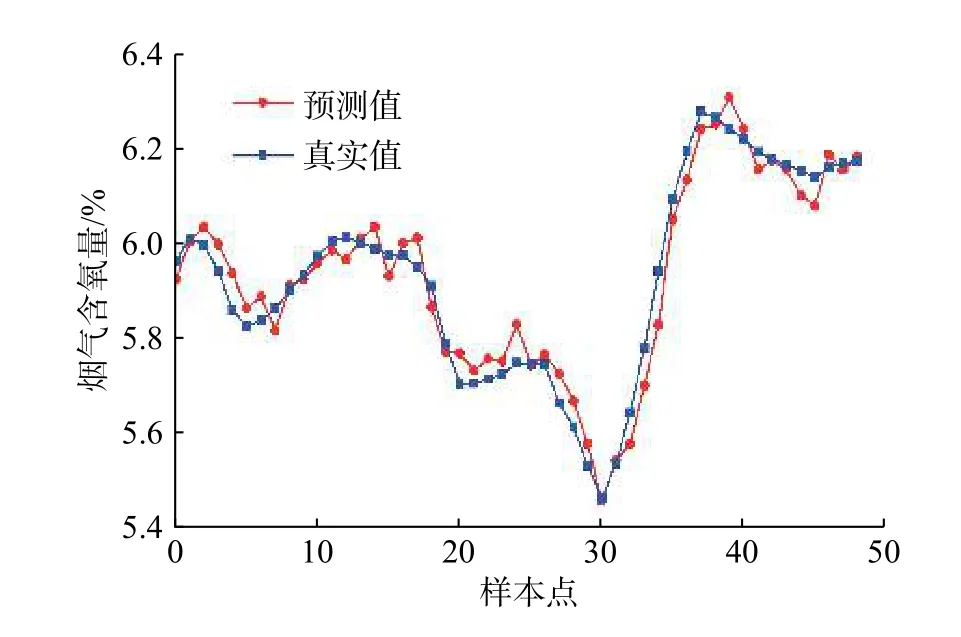
图9 预测值与真实值对比图Fig. 9 Comparison of predicted and true values

从图9可以看出，经遗传算法优化初始权值和阈值的神经网络预测结果与电厂实际数据吻合较好，其相对误差如图10所示。

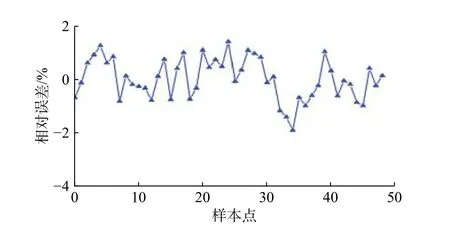
图10 样本点相对误差图Fig.10 Relative error graph of sample points

从图10可以看出，GA-BP模型的相对误差大多集中在[-1%,1.5%]，经计算GA-BP模型的平均相对误差为0.5%。该结论表明，该模型预测结果符合精度要求，且相比于偏最小二乘回归模型，GA-BP模型精度有显著提高。

锅炉烟气含氧量的预测结果是由多个输入参数共同决定的，在电厂的长时间运行过程中测量模型输入变量的传感器极有可能产生测量误差，导致测量数据偏离电厂实际运行值。在对锅炉的烟气含氧量进行实时预测时，训练好的模型应该能够保证在输入参数发生偏差时，依然可以测出较准确的结果。为此对耦合模型进行了鲁棒性检验，在输入参数上附加了1%～5%的随机量。图11为附加随机量的回归结果，图12为附加随机量相对误差曲线。

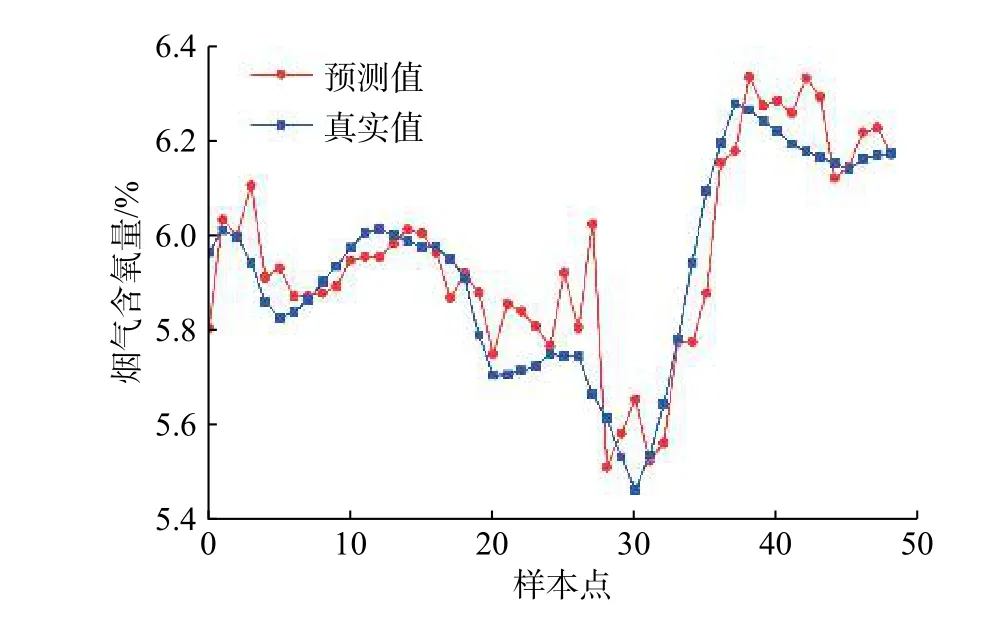
图11 附加随机量的预测值与真实值对比图Fig. 11 Comparison of predicted and true values with additional random amount

从图12可以看出，在输入参数上附加了1%～5%随机量的模型预测结果的相对误差大多集中在[-2%,3%]，经计算平均相对误差为1.48%，依然比较小。由此可见训练好的GA-BP模型受输入参数的影响较小，表明此模型具有很好的稳定性并具有较高的鲁棒性。

图12 附加随机量样本点相对误差图Fig. 12 Relative error graph of sample points with additional random amount

基于上述研究，为进一步验证GA-BP模型准确性，应用GA-BP模型研究了总风量、给煤量对烟气含氧量的影响。首先，控制排烟温度、给水流量、机组负荷、给煤量、主蒸汽压力5个参数不变，逐步增大总风量且在正常范围内取值，总风量和烟气含氧量关系如图13所示；其次，控制这5个参数不变，逐步增大给煤量且在正常范围内取值，给煤量和烟气含氧量关系如图14所示。

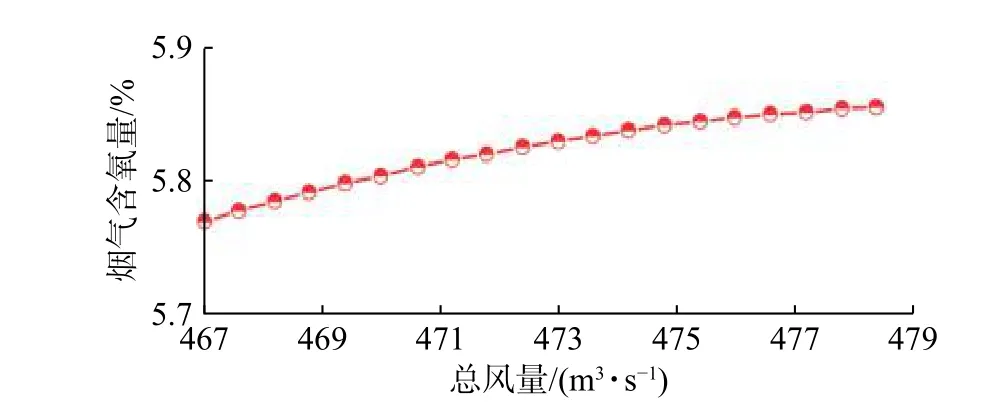
图13 总风量对烟气含氧量的影响Fig. 13 Effect of total air volume on oxygen content in flue gas

从图13可以看出，随总风量的增加，烟气含氧量也随之缓慢增加。这主要是因为此时炉膛内的氧气量充足，随着总风量的增加进入到炉膛里的氧气含量增加，当其他工况不变时随烟气排出的氧量便有所增加。图14表示了给煤量对烟气含氧量的影响情况，由图可知，在其他条件不变的情况下，随着给煤量的增加，烟气含氧量随之减小。这主要是由于给煤量增加，煤炭燃烧所消耗的氧气量增加，排出锅炉的烟气里的含氧量随之减小。图13和图14的研究结果表明，GA-BP模型的预测结果与锅炉燃烧机理完全相符，从而进一步验证了模型的准确性。

图14 给煤量对烟气含氧量的影响Fig. 14 Influence of coal feed rate on flue gas oxygen content

5 结论

烟气含氧量不仅是反映风煤比投入情况的重要参数，而且是锅炉热效率和排污率的重要指标。实时准确的测量烟气含氧量对锅炉运行优化具有重要指导意义。针对火电厂锅炉烟气含氧量测量准确性难以保持等问题，本文用GA-BP模型对电厂的排烟温度、给水流量、机组负荷、总风量、给煤量、主汽压力进行了建模用以预测烟气含氧量，结果显示GA-BP模型模型可以较好地反映电厂的烟气含氧量变化，并且具有很好的稳定性。用GA-BP模型检验总风量、给煤量对烟气含氧量的影响，其结果与锅炉燃烧机理完全相符，从而进一步验证了模型的准确性。GA-BP建模技术为电厂的烟气含氧量测量提供了新的技术手段，同时也为电厂运行人员提供一个很好的参考。由于数据样本有限，各个运行工况数据不足，影响了GA-BP模型的泛化能力，可在得到充足数据后重新训练GA-BP模型，从而提高GA-BP模型泛化能力。