分批补料反应过程的非固定终端经济优化控制

汤舒淇，薄翠梅，俞辉，李俊，张登峰，张泉灵，金晓明

（1南京工业大学电气工程与控制科学学院，江苏南京 211816；2南京工业大学智能制造研究院，江苏南京 210009；3浙江大学控制科学与工程学院，浙江杭州 310027）

引 言

随着现代社会对多品种、高质量、精细化大宗化工产品的迫切需求，当前我国石化行业的生产正向着原料多元化、产品高值化发展。由于间歇、半间歇的生产模式更适合生产小批量、多品种、高附加值的产品，因此更受青睐[1-2]。间歇、半间歇生产与连续生产的区别主要在于它的生产操作范围不局限于传统意义上的稳态点，同时因为间歇生产的时间有限性，必须对整个生产过程进行有效的排产，这给生产带来了灵活性，但也给过程优化控制带来了困难[3]。

目前大部分优化与控制理论方法都是以连续过程为研究对象，通过将批次反应的终端状态固定，终端状态作为优化的终端约束，可将用于连续过程的优化控制方法应用到批次生产中，从而解决批次过程经济优化问题[4]。批次过程优化问题的求解通常采取直接法或间接法。间接法指利用变分法等最优化原理得到问题的数学解析解。例如采用基于庞特里亚金最大原理的优化方法，以求取在批次生产周期终点固定时间下产物浓度最大化的最佳操作曲线轨迹[5]。直接法是将状态变量或输入变量离散化，把原动态优化问题转化为非线性规划问题（nonlinear programming,NLP）。例如因非线性约束导致的解析解计算困难，可对控制输入变量进行参数化以找到最佳的批次过程操作条件[6]，或用有限元正交配置法彻底离散化优化问题[7]。而离散化后的NLP则可以用各类基于梯度或随机搜索算法计算求解，如文献中将改进的蚁群算法用于发酵过程中基质流加率控制轨迹的动态优化[8]。

由于不确定的干扰会导致反应持续时间不确定，因此固定的批次终端优化方法在很多场合不再适用。在不确定干扰下固定终端约束对于批次补料过程是不经济的[9]。这是因为预先设定生产目标的条件并不适用于外部条件改变后的生产。例如，在不确定的系统参数下，将分批发酵过程的自由终端时间和反应物初始浓度作为优化调节变量，根据发酵的实时状态变化随时调控操作参数，获取最佳的发酵品质[10]。对于多批次迭代学习进行计算的情况，不固定终端将带来批次不等长的情况，通过搜索相似的模式分别构造它们对应的置信区域[11-12]。抑或通过混合时间标度策略可将自由终端时间的优化问题转化为固定终端时间的优化问题[13]，为解决不等长批次的批间学习提供了较好的参考。

在没有终端约束的情况下，对于间歇生产的操纵优化而言，操纵变量可行域通常会增加。对于计算量过大且无法通过相关约束缩小可行域简化计算的大型化工生产过程来说，通常采用贯序优化或双层优化的结构[14]。双层优化是指上层通过经济优化计算操纵变量的最佳操作轨迹[15]；底层以上层的优化结果作为固定参数，通过基于优化的最佳操作区域内寻底层局部最优控制，例如用模型预测控制（MPC）实现快速跟踪控制[16]。该结构成功地将经济优化问题和控制问题分离开，以降低解决问题的复杂性，已广泛应用于复杂化工过程优化系统。然而双层优化结构的潜在缺点是上下层所采用的不同模型会导致优化效果偏离预期[17]。因此，近年提出将操作优化和最优控制集成到同一层的单层优化控制方法。为了提高单层优化控制的鲁棒性，设计了鲁棒的状态估计和退避约束的方法[18]；另外一些研究者采用了一种复合优化目标函数，同时考虑了过程产量和目标函数敏感性[19]。文献[20]还提出了一种基于NMPC和DRTO的批次协同优化控制方法，使NMPC更加适用于批次生产过程，可以同时考虑批次生产长度对经济的影响。在单层的优化控制中，应用了滚动时域控制（receding horizon control,RHC）的单层优化控制又可以视为一种经济模型预测控制（economic model predictive control,EMPC），应用于反应过程中的研究[21-24]。例如文献[25]通过为同一过程制定不同的EMPC经济目标函数，以实现不同的经济优化效果。也有文献研究了非固定终端的收敛性问题[26-27]，但利用EMPC目标函数的多样性，将非固定终端约束应用于批次经济优化控制研究成果并不够充分。

因此在上述研究的基础上，提出了一种应用于分批补料的非固定终端经济优化控制方法，用于考虑批次生产长度对经济的影响，解决批次周期不确定约束优化控制问题。本文基于经济模型预测控制方法，提出了非固定终端的经济优化问题；提出控制变量差异参数化的方法提高优化计算效率；采用内点罚函数法求解带非线性等式、不等式约束的优化问题；给出了基于滚动时域的优化控制方法及其流程图；在苯胺加氢分批补料工艺中进行了实验测试，并与多回路复杂PI控制进行了对比研究，以验证该方法的有效性。

1 非固定终端优化控制

1.1 优化问题的提出

任意被控对象动态过程，反应过程可以写成如下常微分方程组（ordinary differential equations,ODEs）形式：

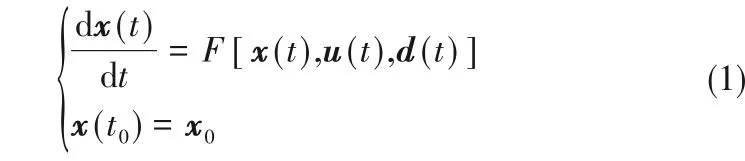
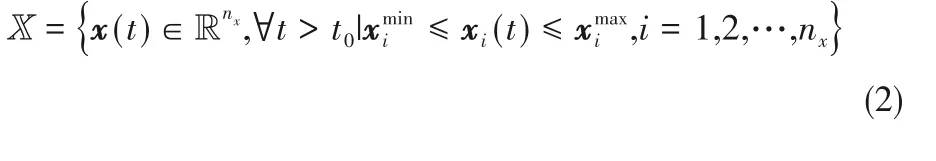
令优化求解的初值x(ts)=xs，u(ts)=us，ts为优化时的当前时刻，定义一个包含(xs,us)的不变集Ω，且Ω⊆X×U，则x(t),u(t)∈Ω代表在约束内u(t)的作用下x(t)也处于约束内。

在连续过程中，EMPC通过在滚动时域算法中求解含经济目标函数的最优化问题，实时更新系统的运行条件。该优化问题形式通常如下：

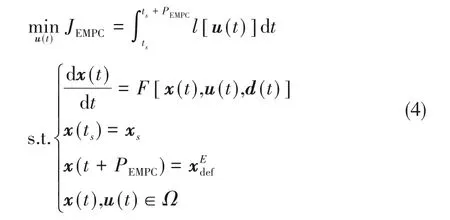
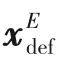
但将EMPC应用到间歇生产过程时，则需要考虑如下问题：（1）间歇生产无稳态点，也因此不存在预测范围内需要达到的设定点；（2）间歇生产的生产时间有限，如果预测范围PEMPC保持不变，随着时间的滚动,预测范围将超过生产时间范围。

因此考虑将针对连续过程提出的EMPC应用于间歇生产过程，并且对间歇生产模式提出有针对性的改进。EMPC策略在连续过程中的收敛性通常通过增加预测时域范围来保证。根据文献[26]，随着优化范围的增长，系统性能会收敛到最佳状态，相较于无限时域优化有指数级误差衰减。因此优化时域应当在可计算范围内足够长。对于批次反应过程来说，最长的有效预测时域即批次的终端，则优化预测时域P=Tf-ts，以获得足够的收敛性能。假定间歇生产的一个批次周期为Tf，用批次结束时间的产量约束x(Tf)=xf代替预测范围内的设定点，以达到预先设定的生产目标。因此在每个采样点要解决一个固定终端的最优控制问题，如式（5）所示：

终端时间放宽后，对于经济目标函数的定义也能不局限于最小化控制输入。原本的生产计划指标是通过一个终端等式约束达到的，给求解计算带来了很大的复杂度。由于实际生产中的经济目标通常是利益最大化。

通过将目标函数以最大化利益的方式设置，即可将原本的生产计划指标的等式约束转化为产品收入项；将原本的最小化控制输入目标函数，转化为生产成本项。最终达到最大化利益生产的目标。而根据间歇过程的生产特点，产品收益通常在一个批次生产完成之后才会产生，即在目标函数中只有终端项。而生产成本则是在生产前有一次性成本，在整个生产过程中有连续累积的成本，因此既有终端项又有积分项。完整的经济目标函数形式应当如下：

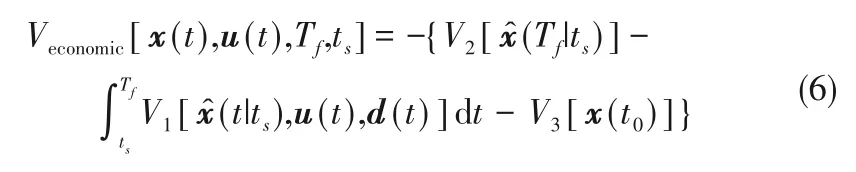
其中，Veconomic、V1、V2、V3分别为过程经济利益函数、累积成本函数、产品收益函数、生产前一次性成本去量纲后的函数，V3通常是一个常数。经过改进后非固定终端的优化控制问题如式（7）所示。

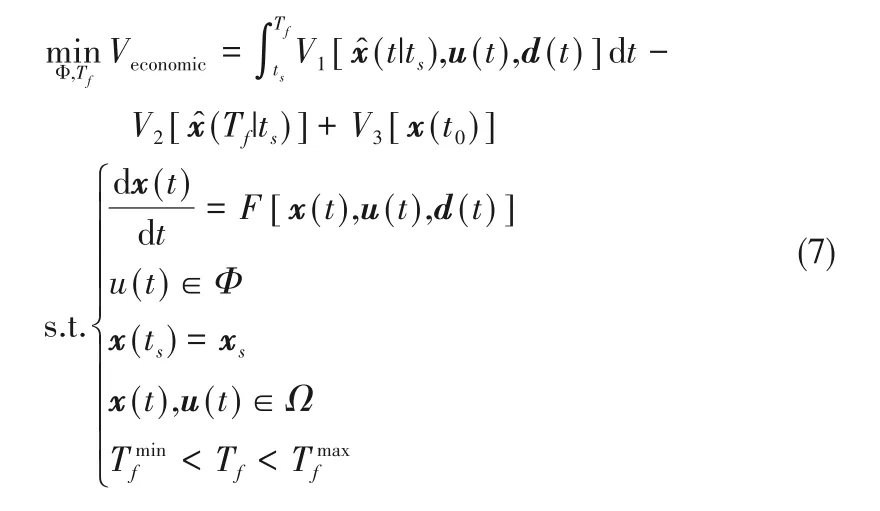
在t时刻的最优控制输入序列集为Φ，它是一系列控制变量的集合。这是因为当终端不固定的情况下，不同的操纵变量有不同的离散化规则，具体在1.2节中介绍。

可以观察到，上述表达式计算的是一个动态经济优化问题，且通过计算动态经济优化和在每个采样时刻更新系统状态，将开环优化转化为反馈控制策略。当不考虑过程干扰以及模型失配等不确定性因素，该优化问题在最初一次求解得到的最优终端时间与后续过程中计算得到的最优终端时间应当是一致的。而发生扰动后，经济最优的情况会使Tf趋向更有利的区间。而反应最终的产物x(Tf)将由优化问题根据过程情况与经济条件调整。

1.2 控制轨迹与状态变量平稳性

式（7）的动态优化问题通过优化计算的目标函数来优化控制输入变量，可以最大程度地降低过程成本。但是，由于该优化中存在较大的可行域区间，所得的控制输入的最佳轨迹并不一定适合化工生产的实际过程。操纵变量的反复大跳动与引起的状态变量急剧增减可能会在运行过程中损坏设备，或使具有高敏感度的系统进入失控状态。为限制状态变量或操纵变量的跳变，可在约束中加入导数或累积上限。但是如果遇到确实需要较大跳变才能抵消的大扰动，该约束会限制控制动作的行为，以至于控制可行性不高。因此，在原目标函数加入限制重要系统状态变量的导数和操纵变量的累积差项，这样当经济项大到可以忽略控制平稳项时，意味着需更新控制动作。更新的目标函数如下：

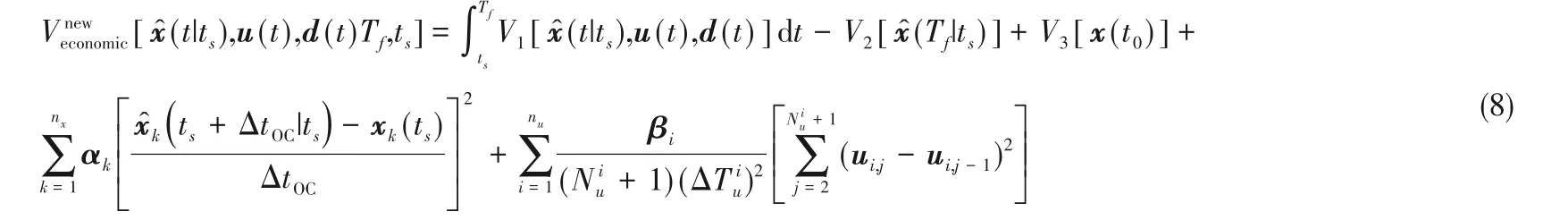
其中，α和β分别是维度为nx与nu的加权因子向量，α的第k个和β的第i个分量分别对应系统状态变量平缓变化的程度和控制输入变量的稳定变化强度。

2 控制变量的参数化

在解决式（7）的优化问题中，使用控制变量参数化法（control variables parameterization,CVP）描述控制变量的轨迹。在控制变量参数化方法中，只有控制变量被离散化，而其他变量则仍然按照连续的考虑。控制变量的参数化给无限维的优化问题转化为有限维的NLP提供可能，而保留其他向量的连续特性又大幅度降低了求解规模。

面对批次反应过程的反应周期不定的情况，使用传统的固定网格化离散方法固然是一种可行的方法，然而该方法下，并不能根据过程动态特性自主选择不同控制变量的微调精度。另外，若要更精确地逼近最优控制轨迹，就要将网格宽度设置得短一点，也增加了网格数量，且加大了NLP的维数和计算量。因此对于不同控制变量的参数化定义方法非常重要，这里选择了根据控制变量动态特性合理确定网格，并且随着迭代实时更新的控制序列分段方法，如图1所示。

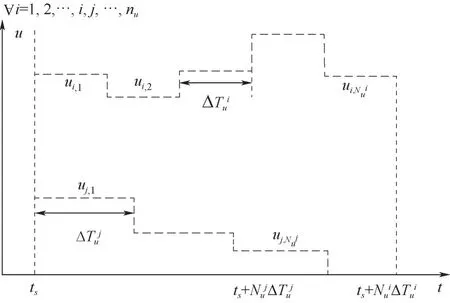
图1 控制变量的独立参数化示意图Fig.1 Schematic diagram of control vectors respectively parameterized

由于批次终端时间并不事先可知，因此当优化所得的批次终端时间变化时，需要在每个优化问题求解之前（即当前时刻ts）时更新分割参数，如式（9）和式（10）所示。

这两个更新公式分别对应于控制范围超过预期的终止时间和控制范围与预期终止时间的比例小于ωi。其中ωi是一个无量纲参数，表示第i个控制变量的控制时域在一个批次周期中合适的占比。

3 优化问题的求解

为解决优化问题，本文将采用内点最优化法（interior point optimizer,IPOPT）进行求解，它通过在目标函数中添加障碍项消去不等式约束，并通过迭代减小障碍权重，不断逼近最优解。通过控制变量参数化方法将式（8）中的优化问题转化为NLP后即可以直接求解，但所需求解的问题是一个含有非线性等式约束、不等式约束的较为复杂的约束优化问题。为了降低求解难度，采用了ODE求解集成和障碍函数法分别解决等式、不等式约束，将有约束的NLP转化为无约束的NLP来求解。

式（7）问题中的等式约束即过程模型的微分方程，将微分方程的求解记作算子D(·)，则t>ts阶段的状态变量的预测值，通过ODE求解器所求的解可以表达成如下形式：

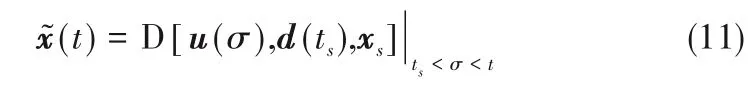
其中，边界条件x(ts)=xs，且ts<σts)时刻状态变量的数值解x͂(t)。在目标函数式（8）中将所有的状态变量用式（11）替代，即将微分方程的数值解集成到目标函数的计算中，则自动满足等式约束。则新的优化问题转化为如式（12）所示的NLP。

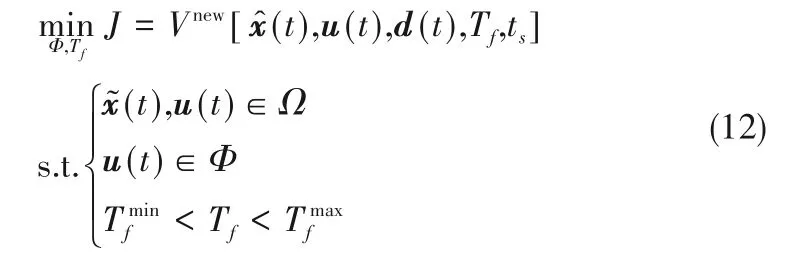
考虑到一些优化问题的极小值点可能位于可行域的边界上，为得到这样的极小值点，内点罚函数需要在迭代过程中不断调整罚因子来逐步削弱障碍函数对最优值点的影响，从而使算法产生的点列在可行域内部逐步逼近原规划问题的极小值点。本方法适合处理求解最优解在可行域边界上但在靠近可行域边界时有次最优解的问题。考虑如式（12）所示的优化问题，通过控制变量参数化后优化操纵变量为m=[u'1,…,u'nu,Tf]'，不等式约束条件用fi表示，ncon是约束条件的个数，即可行域内点集为：

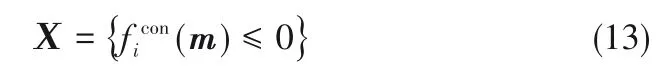
建立惩罚项

其中，π是惩罚障碍权重，fbarrier为障碍函数，为了获得连续梯度，选取对数形式：

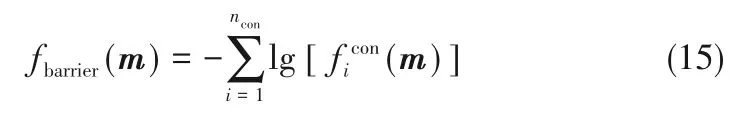
给定初始π0>0，m0∈X，权重衰减系数γ>1，允许误差δ>0。求解P(mk,πk)的近似最优解，即|∇m P(mk,πk)|≤δ，如果fbarrier(mk)/πk>δ则令πk+1=γπk，否则结束迭代计算，而近似最优解即为mk。

假设存在最优解m*，则同时存在对偶最优变量λ*与原始操纵变量一同满足Karush-Kuhn-Tucker（KKT）条件：

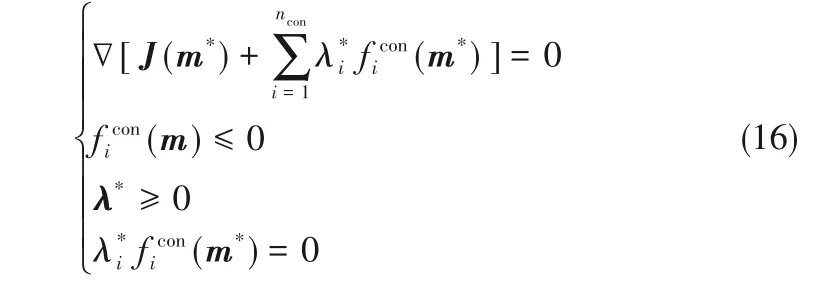
在这个问题中，λi可相当于

且

则当π→∞时，互补松弛条件成立，即内点法产生的最优解相当于满足KKT条件。

4 非固定终端经济优化控制流程

非固定终端经济优化控制遵循滚动时域优化控制，直到满足终止条件为止。如图2所示，在初始化系统后，根据式（8）的目标函数和式（7）中的等式、不等式约束，形成一个动态优化问题。根据当前的测量信息[x(ts),u(ts),d(ts)]，用式（11）将ODE求解器集成到目标函数的计算中，用以根据当前时刻状态估计未来时刻状态变量的值。通过CVP离散化操纵变量，将动态优化问题转化为NLP。通过IPOPT方法求解带有边界约束的NLP，从而获得最优批次生产时间Tf*与最优操纵变量序列uij*，以ΔtOC执行操纵变量，依据式（9）、式（10）更新Nu，并且向前推进ts。通过判断Nu的个数判断所剩时间是否不足以进行一次优化控制，如果小于1则不再进行优化求解，再根据时间ts是否达到Tf结束一批次的生产，否则，重新测量当前状态信息，在下一时刻重新求解优化问题。

图2 非固定终端经济优化控制流程Fig.2 Flow chart of economic optimization control with unfixed terminal

根据流程图，非固定终端经济优化控制的具体步骤如下：

（1）初始化参数设置与初始操作条件;

（2）从时间ts开始，根据优化问题式（12）求解出最优控制参数集（Φ*）和最佳批次终端时间（Tf*），并计算终端状态与该时刻下的经济目标函数；

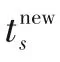
5 实验测试

5.1 分批补料反应过程机理模型

本算法使用的测试案例来自文献[28]的苯胺（aniline,A）加氢制环己胺（cyclohexylamine,CHA）模型，其反应方程式如下：

苯胺加氢通常采取批次生产的模式，在连续搅拌釜式反应器内一次性加入苯胺，然后以批次或半批次的方式加入氢气，反应是放热的，需要对反应器降温以带走多余的热量。反应所需的夹套换热反应器如图3所示。

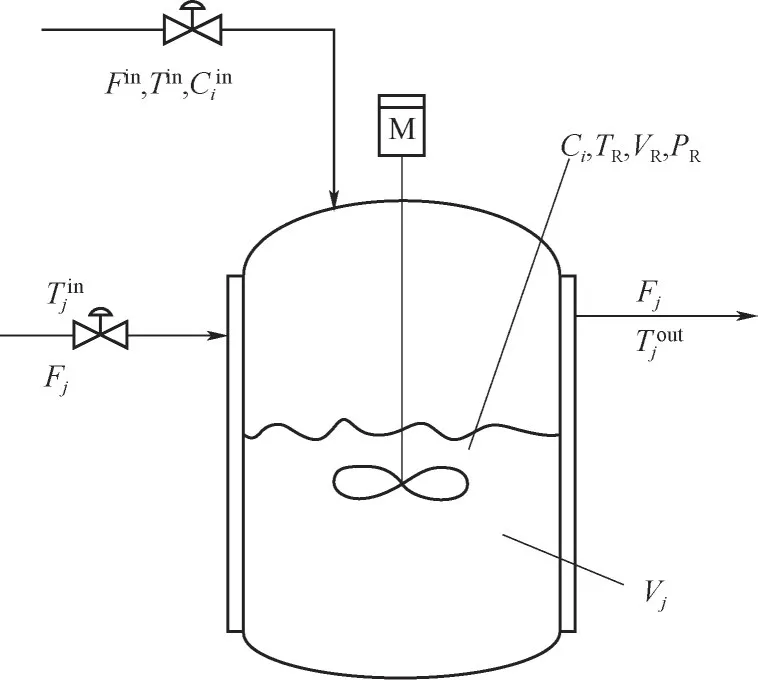
图3 分批进料反应器示意图Fig.3 Schematic diagramof fed-batch reactor

描述该系统的动态数学模型由总质量平衡、3个成分的平衡、反应器液体上的能量平衡和夹套能量平衡组成。

假设密度恒定，质量平衡如下：

其中，Fin是氢气进料的体积流量，VR是容器内反应物的体积。

成分平衡如下：

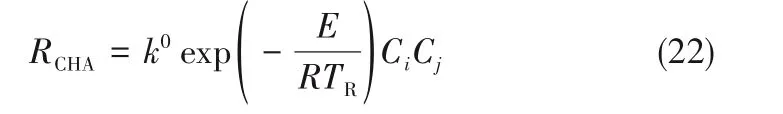
反应器的能量平衡如下：

夹套的能量平衡如下：

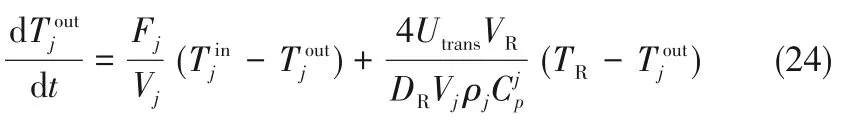
反应器压力由温度和液体组成计算得出，苯胺和环己胺的蒸气压常数以及氢的亨利定律常数是使用Chao-Seader物理性能数据包从Aspen Plus获得的数据计算得出。

其中，Xa、Xb、Xc分别为苯胺、氢气、环己胺在反应器中的摩尔分数。

5.2 目标函数的设置

苯胺加氢过程的经济目标函数设置如下：

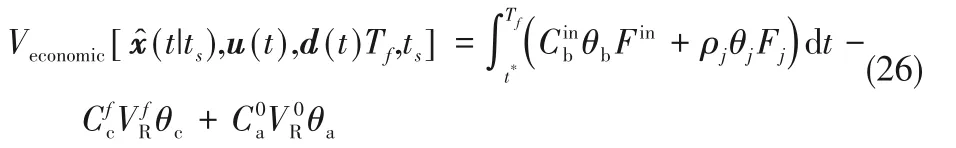
其中，上角标“f”代表t=Tf时各种变量的值，从其物理意义中可以看出，经济目标函数的值即过程加料、冷却水消耗和一次性投料的成本减去产品收益。然而由于实际上的目标函数还有关于稳定运行的项，因此会将经济函数的数量级缩放到0～1之间，即在Veconomic外乘系数ε=1/Vmax，Vmax是理论上能达到的最大收益，即不需要任何成本，将所有一次性投料都转化为产品所能获得的收益。然而实际上这是不存在的，所以经济项永远小于1。

在约束条件的问题上，各个操纵变量、状态变量的边界约束不仅包括生产时的物理约束、安全约束，还包括根据实际化工过程经验所得的可行约束。即根据所需产品的质量，估计推导出操纵变量的操纵范围，并作为过程约束加在优化问题中。由于无终端约束，收紧了过程约束，因此求解的速度大幅度提升。在无扰动发生时，生产目标的可达性有了新的保障。而大的扰动发生时，生产指标达到的概率急剧降低，此时基于最大化收益的优化方法也能极力止损。

进料流量的变化会引起苯胺加氢反应过程系统状态发生更大的变化，而系统状态变量中需要进行安全约束的主要就是氢气浓度和反应器温度，反应器压力和冷却剂出口温度也几乎完全分别取决于这两个变量，因此为了限制温度上升的速度需要对温度经行斜率限制。除此以外，开环下整个批次的时间大约在300 min以内，取控制范围在预测范围的1/10左右，为了对过程速率有更加细致的控制，将氢气进料的控制变量离散化参数设置得比冷却剂进料参数更细腻。因此针对α、β、Nu、ΔTu四个参数的整定结果见表2。

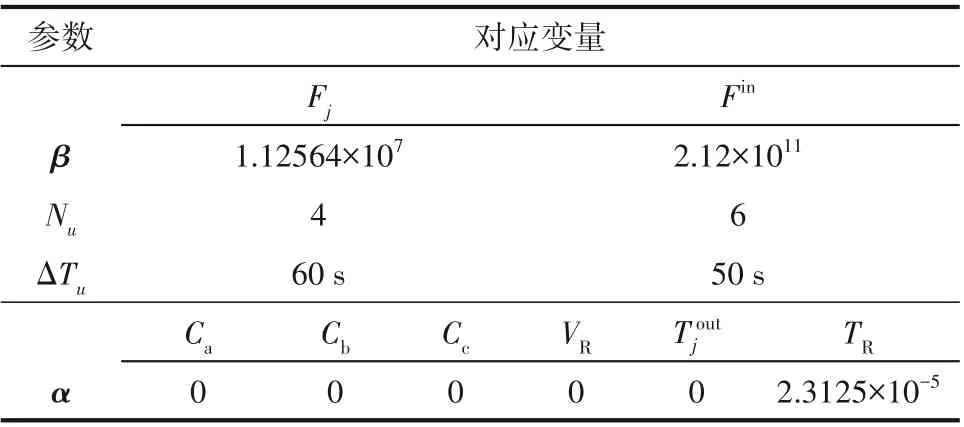
表2 优化过程的参数整定Table 2 Tuning parameter settings of the optimized control

5.3 仿真测试

基于上述苯胺加氢反应模型，采用C++语言进行批次反应过程控制与优化仿真，实现环己胺制备过程的单批次周期的最优化。为了测试本方法在变批次长度上的优势，将优化控制与选择与分程结构的多回路PI控制进行了对比。PI控制的条件设定参照文献[29]用离线优化得到的最佳参数运行，分别用冷却液进料与氢气进料进行独立回路控制，再为氢气进料增加低选控制结构，避免进料导致压力过大，而温度控制采用两种输入的分程控制结构。PI控制的参数调节依据文献[30-31]，为KcTC=0.05，TiTC=10 min，KcPC=0.3，TiPC=30 min。在50 min时对冷却剂入口温度加入了扰动，从350 K升高到400 K，分别测试了有无扰动状况下的两种方法控制输出情况对比，见图4～图9。

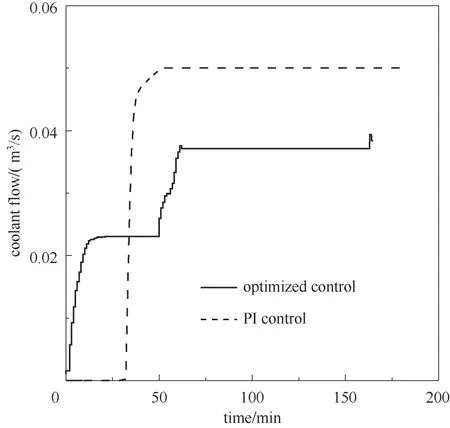
图4 有扰动下冷却水流量曲线对比Fig.4 Comparison of coolant flow with disturbance

控制稳定性如图4和图5所示。在PI控制下所需的冷却剂用量明显多于优化控制下，扰动发生时控制变量也发生了振荡。相比本文提出的优化控制方法的控制曲线一直处在可接受的变化速率中。从图6和图7中在扰动发生时温度、压力这两个重要被控变量曲线来看，PI控制下的压力曲线在扰动发生时总是会出现振荡。实际上，在反复调试PID参数后发现扰动带来的振荡是与反应机理模型相关的，是单回路闭环控制不可避免的。而优化控制采用一种滚动优化控制的策略，通过求解一连串控制序列和预测状态变量可以很好地避免振荡的发生。

图5 有扰动下进料流量曲线对比Fig.5 Comparison of feed flow with disturbance

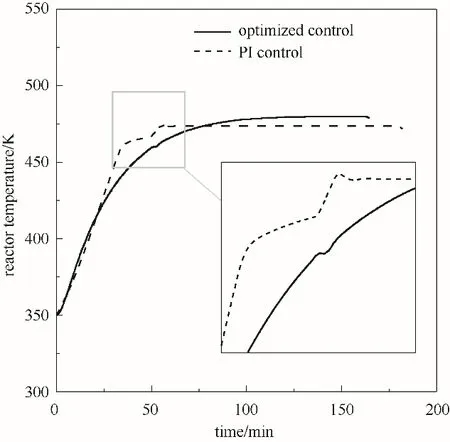
图6 温度控制抗扰动Fig.6 Anti-disturbance comparison of temperature control

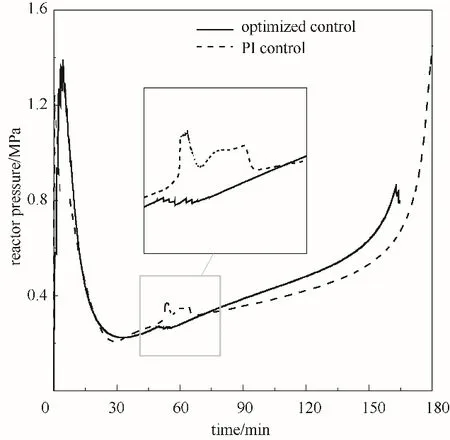
图7 压力控制抗扰动Fig.7 Anti-disturbance comparison of pressure control

反应终止时间如图8和图9所示。在扰动的影响下批次的反应明显变缓慢了，这是因为温度升高后必须降低送料速度，以避免反应器内温度超标。因此两种控制方法下批次终止时间都变长了。除此以外，可以观察到PI控制下的反应在接近反应结束时，反应速率急剧下降。根据式（22）可以推断出，此刻反应器中的苯胺浓度较低，则反应速度会下降，为了促使反应的继续，则需要提高另一种反应物的浓度，即需要向反应器中加入大量的氢，促使反应速率保持在较高的水平，这也是反应器中压力在这段时间骤然升高的原因。在PI选择控制的策略下，压力过高时选择牺牲温度控制。对于优化控制而言所有变量都在同一个优化中求解，因此压力过高的情况在预测、优化中被避免了。

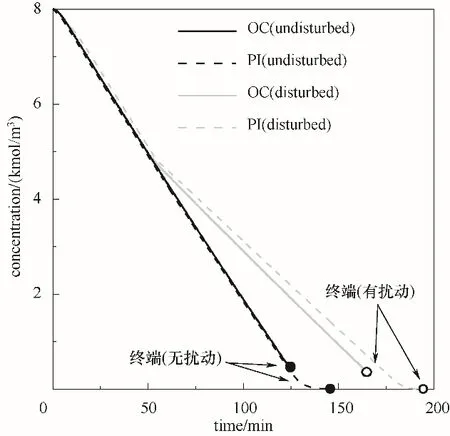
图8 反应器内苯胺浓度变化Fig.8 Changes of aniline concentration

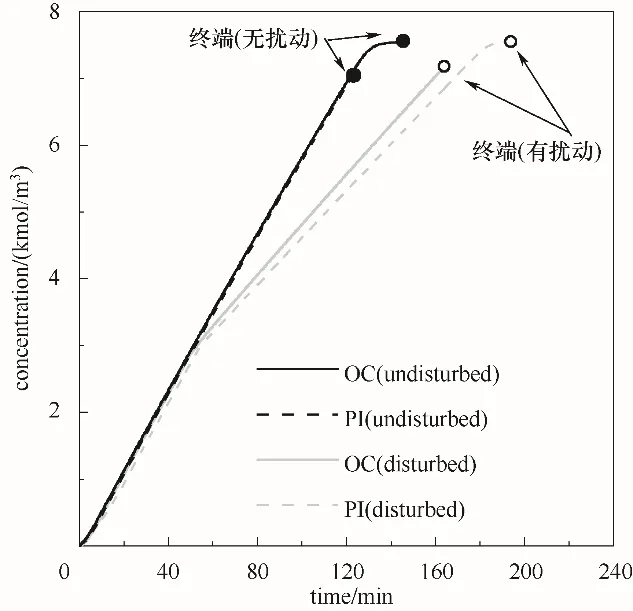
图9 反应器内环己胺浓度变化Fig.9 Changesof cyclohexylamine concentration

两种控制下的反应经济情况如表3所示。其中的净收入计算方法是：净收入=反应产物获益-反应过程消耗（包括一次性投入物料、加料、冷却等消耗）。可以看到无扰动情况下，PI控制的净收入甚至比优化控制要高，因为在无扰动的情况下PI控制的反馈控制足够将反应稳定在较优的操作区间。但是算上时间成本后，PI控制的平均收益则略低于优化控制。在有扰动的情况下，两种控制下的经济收益均低于无扰动，且PI控制的净收入下降了45%，相比之下优化控制净收入降低了25%的情况较好。

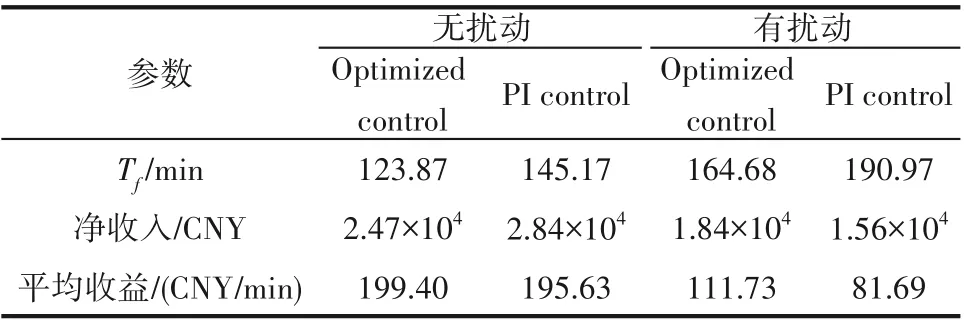
表3 两种控制下的经济情况对比Table 3 Economic profitability of two kinds of control

除此以外，对于分批补料过程的特性，当容器内的一次性投料的反应物浓度低时，需要反应速率大幅下降，大量的投入消耗和时间成本对反应物产量的提升不大。因此在终端不固定的情况下可以获得更多方面的收益。

6 结 论

本文提出了一种分批补料过程的非固定终端的经济优化控制方法，该方法将非固定终端经济优化与多变量协同控制集成在滚动时域控制结构中，可以更好地实现单批次内生产利益最大化。由于将批次生产过程的关键操纵变量和批生产周期的持续时间都视为优化和控制问题的自由度，因此可以较为准确地管理批次生产的终止时间，在反应条件允许范围内最大程度压缩低效率的生产阶段。基于目标函数去预测评估优化最佳操纵变量和操作时间，能够稳定地将过程中发生的不确定扰动引起的偏移尽快反馈调控现有条件下经济更优的操作区间，不断更新关键操纵变量的控制分段函数的分割数及其宽度，从而可灵活优化操纵变量和操作时间的轨迹。单层的经济优化控制算法避免了双层优化控制的滞后性，并且基于惩罚函数内点法的实时优化在有效范围能最快地求解最优轨迹线，解决单批次周期的优化和控制问题，与复杂多回路PI控制对比分析发现，本方法明显更灵活有效，测试结果明显优于基于选择-分程的复杂控制方法，通过优化计算每个批次生产的最佳操作条件及其生产周期，实现批次反应过程生产时间与经济效益的最优化管理。

符号说明

——分别为反应器内苯胺、氢气、环己胺的初始浓度，kmol/m3

——冷却液的比热容，kJ/(kmol∙K)

DR——反应器底部直径，m

Fin,0——加料流量初值，m3/s

Fj0——冷却液流量初值，m3/s

Fjmax，Fjmin——分别为冷却液流量的最大、最小值，m3/s

Fin,max，Fin,min——分别为加料流量的最大、最小值，m3/s

ΔHR——反应放热，kJ/kmol

k0——反应速率常数，m3/(s∙kmol)

Tin——反应物进料温度，K

Tjin——冷却液入口温度，K

Tjout,0——冷却液出口初始温度，K

TRmax,TRmin——分别为反应器温度的最大、最小值，K

TR0——反应器温度的初值，K

Vj——冷却液体积，m3

VRmax,VRmin——分别为反应器内反应物体积的最大、最小值，m3

——反应器内反应物初始体积，m3

θa,θb,θc,θj——分别为苯胺、氢气、环己胺、冷却液的经济参数，CNY/mol

ρj——冷却液的密度，kg/m3