LTNE条件下界面对流传热系数对部分填充多孔介质通道传热特性的影响

李琪，张容铭，胡鹏飞

（东北电力大学能源与动力工程学院，吉林省吉林市 132012）

引 言

自然界与工程实际中有许多涉及多孔介质内的流动和传热现象，如热交换器、催化化学反应装置、过滤设备、太阳能集热器、核能工程、地热工程等。但由于多孔介质内部及其与自由流体界面存在复杂的物质及能量传递，所以在研究过程中采用的流动及传热的模型并不统一。

Vafai等[1]指出局部热平衡模型（LTE模型）是基于假设多孔介质内固相和流相的温度是一致的，因此只有当固相和流相的温差很小时，LTE模型才成立。而在实际应用中这种温差可能无法忽略，因此需要采用局部热非平衡（LTNE）模型进行传热分析。同时，在应用LTNE模型时，还需要在界面处附加一个热边界条件。为了解决此问题，Amiri等[2]首先提出了两种方法，第一种方法（模型A）假设流相和固相根据各自温度梯度和热导率划分总热流，第二种方法（模型B）假设流固两相所接收的热流相等并都等于总热流。Vafai等[3]基于LTNE模型获得了全部填充多孔介质通道内流固两相温度及Nusselt数的解析解，并在此基础上研究了LTE模型的有效性。Mhimid等[4]同时考虑了LTE和LTNE两种模型，数值研究了垂直圆柱形颗粒堆积床内的颗粒干燥过程。Marafie等[5]进一步研究了全部填充多孔介质通道内考虑惯性效应影响下LTE模型的有效性，指出Darcy数和惯性参数对建立局部热平衡假设的有效性影响较小。Alazmi等[6-7]分析了多孔介质中不同流动和热界面条件的影响。数值研究和分析了半无限多孔介质在不同参数下的不同流动和热界面条件之间的差异[6]。在LTNE模型的不同热边界条件下，得到了完全填充多孔介质通道内温度场和Nusselt数的数值解。发现在不同的边界条件下多孔通道的Nusselt数可能有很大的不同[7]。Min等[8]通过假设固相和流相在多孔区交替分布，对部分填充多孔介质平行平板通道中的传热和流动进行了分析，得到了温度场和Nusselt数的解析解，并且该结果与已有的数值和实验结果吻合较好。Dehghan等[9-11]对多孔通道或微通道中具有LTNE条件的热对流发展进行了摄动分析。

上述文献都是基于完全填充多孔介质通道内进行流动和传热分析。而Yang等[12-14]获得了不同热界面条件下全部填充多孔介质通道及中间填充多孔介质通道内流固两相温度及Nusselt数解析解，发现并强调了界面处流固两相的温度梯度分岔现象。Mahmoudi等[15-16]分析了在通道中心处填充多孔介质通道内流体的流动及传热特性。发现当多孔介质填充高度与通道高度之比即多孔介质填充率大于0.6时，LTE模型是无效的，为了以合理的压降为代价使传热效果最大化，多孔材料的最佳填充率为0.8[15]。通过对比模型A与模型B，发现采用模型A所获得的流固两相温差要小于采用模型B所获得的流固两相温差，并且发现当两种模型的多孔介质填充率小于0.9时，整体传热性能与热界面模型的选取及Darcy数的值无关[16]。在体积平均理论的基础上，Ochoa-Tapia等[17]提出了部分填充多孔介质通道的界面热通量条件（模型C），认为界面附近多孔介质区固相的热通量是基于其与自由流区域流体对流换热，并通过该条件确定界面附近多孔介质区流固相热流分布。通过应用上述三种热边界条件（模型A、B和C）并结合速度滑移界面条件，Yang等[18]研究了中间填充多孔介质平行板通道内的传热特性，推导出LTNE模型下的温度场精确解，并讨论了不同热边界条件之间的关系。Xu等[19]基于LTNE模型并结合模型C及速度和动量均连续界面条件研究了部分填充金属泡沫通道的流动和传热特性，分析了孔密度、孔隙率、Reynolds数及多孔层填充厚度等参数对流动和传热的影响。Torabi等[20]采用LTNE模型并结合模型A分析了底部填充多孔介质非对称通道内的传热，发现了Nusselt数、温度场和熵产率的分岔现象。后来，Torabi等[21-22]分别研究了模型A和C下的部分填充多孔介质通道内的强制对流传热，得到了温度场和熵产的半解析解，着重分析了热导率比、Biot数、Darcy数、流固两相的内热源项等对通道传热的影响。Li等[23-24]采用LTNE模型并结合模型A分析了部分填充多孔介质通道中的传热，得到了温度场和Nusselt数的解析解和精确解，分析了应力跳跃系数对传热和流体流动的影响，并讨论了LTE模型的有效性[23]，引入内热源后，发现Nusselt数的精确解存在奇异性，并对这种奇异性现象进行了分析[24]。

综上所述，前人对于部分填充多孔介质通道内传热特性的研究中，几何模型、多孔介质内部和界面区的动量及能量传递模型都有所不同。而在考虑局部热非平衡时，针对模型C下界面附近的对流换热的研究还不够充分，特别是目前的研究都是基于速度和应力均连续的界面条件进行的。因此，本文针对部分填充多孔介质通道，在多孔介质区采用Brinkman-extended Darcy模型及LTNE模型并结合应力跳跃及模型C界面条件，得到了通道各区域流相及固相温度分布和Nusselt数解析解，并在此基础上分析和研究界面对流传热系数、Darcy数、空心率、固流两相热导率之比以及Biot数等对通道传热效果的影响，比较界面对流传热系数与界面应力跳跃系数分别对部分填充多孔介质通道内传热效果的影响，并进一步分析了本文基于模型C所获得的传热特性与前人模型A所得结果的区别及联系。

1 物理及数学模型

1.1 部分填充多孔介质通道物理模型

如图1所示，本文研究的物理模型为两侧对称布置等高多孔介质层的平行板通道。通道壁面施以恒热流。通道的总高度为2h0，自由流体区的总高度为2hf，则空心率S=hf/h0。假设通道中的流体是由水平压力梯度∂p/∂x驱动的不可压缩层流，强制流动换热充分发展，多孔介质各向同性且流体饱和渗透，渗透率、孔隙率、热导率等物理参数均为常数。

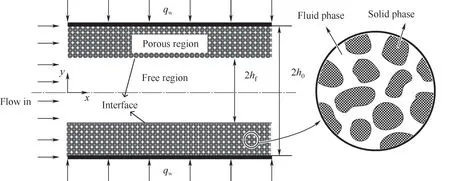
图1 多孔介质-自由流体通道物理模型Fig.1 Physical model of the porous-fluid channel

1.2 部分填充多孔介质通道数学模型

假设通道内流体运动状态为水平压力梯度dp/dx驱动的充分发展层流状态且y方向压力梯度为0（即（-∂p）/∂y=0），流动与换热充分发展，忽略自然对流和辐射换热的影响，忽略热弥散和黏性扩散的影响，则流体流动与换热控制方程可简化[13,15-16,23]，其中自由流体区的运动方程为：

多孔介质区的运动方程采用Brinkmanextended Darcy模型:

式中，uf和up分别是自由流体区和多孔介质区的流体速度，μf表示自由流体区流体的动力黏度，μeff表示多孔介质区流体的有效动力黏度，p为压力。上述运动方程对应的流动边界条件为：

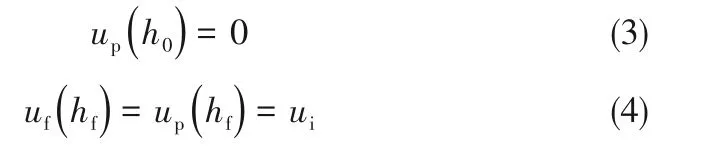
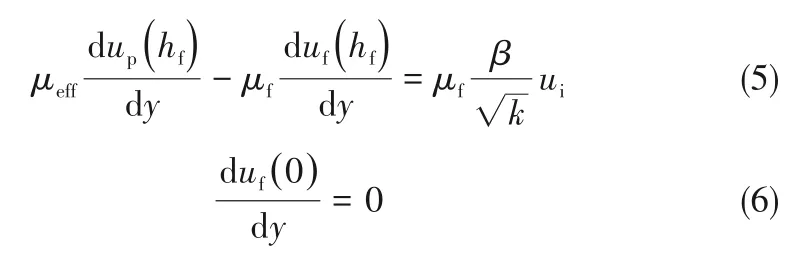
式中，ui是流体在界面处流速，β为界面应力跳跃系数。如式（5）所示，本研究将采用Ochoa-Tapia等[25]提出的界面应力跳跃条件。并且Ochoa-Tapia等[26]发现β的值在-1～1.5之间时界面应力跳跃条件与Beavers等[27]提出的速度滑移模型吻合良好，当β=0时该条件为应力连续性界面条件。

自由流体区的能量方程为：

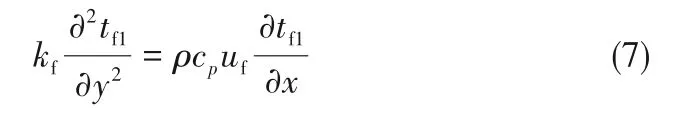
多孔介质区流相和固相的能量方程分别为:

式中，tf1和tf2分别表示自由流体区和多孔介质区的流相温度，ts为多孔介质区的固相温度，kf是自由流体区流体热导率，kef和kes分别为多孔介质区流相和固相有效热导率，hsf为流体与固体之间的对流传热系数，asf为多孔介质区流相与固相之间接触的单位面积。热边界条件为：

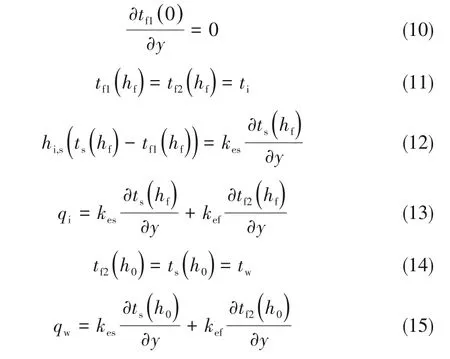
在本研究中，利用模型C[式（12）]为热边界条件来获得温度分布和Nusselt数Nu的精确解。其中hi,s是界面对流传热系数。将式（7）从0到hf积分：

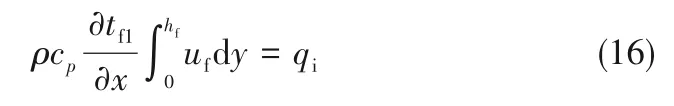
将式（8）和式（9）相加，并将结果从hf到h0积分，可得：

将式（11）和式（12）代入式（17），得:

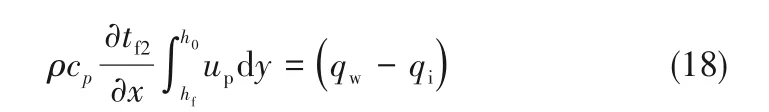
其中，um定义为通道内的平均速度:

在模型C下，qi和qw之间的关系可表示为:

2 数学模型解析解

2.1 方程无量纲化

为了减少方程变量，引入下列无量纲化参数:

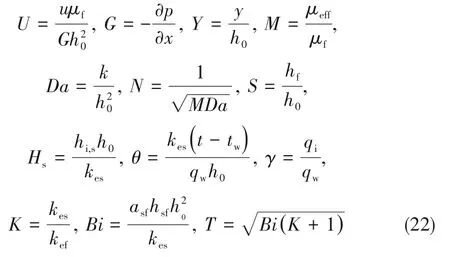
将无量纲化参数代入式（1）～式（6），可得到无量纲化的运动方程

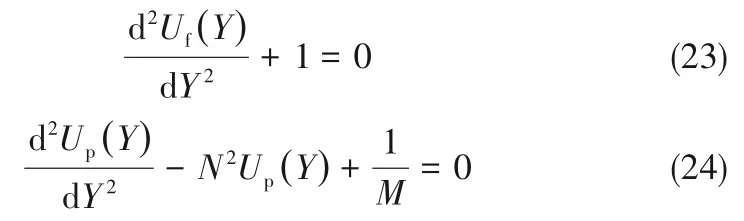
及其边界条件：

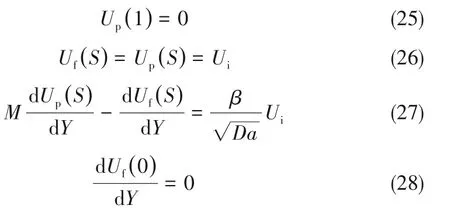
联立式（23）～式（28）可以求解上述微分方程并得到通道内各区域速度分布的解析解，具体求解方法可参考文献[28]。文献[28]对底部填充多孔介质通道内流体流动特性进行了研究，其方法类似。本文通道内速度分布的解析解与Li等[23]得到的结果一致，其为：

其中

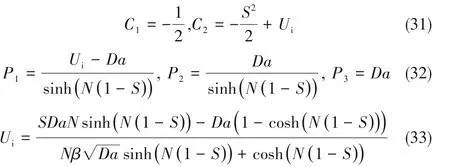
把式（29）～式（33）代入式（20），通道内的平均流速为：

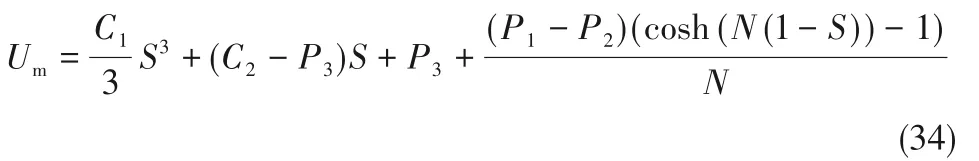
根据式（21）和式（22），界面热流之比的无量纲形式为：

将式（29）～式（33）代入式（35），结果为：

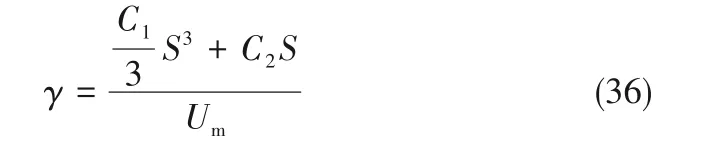
2.2 温度分布

将式（22）代入式（7）～式（15）为模型C下的无量纲能量方程和热边界条件：

通过Matlab编程求解式（37）～式（45）可以得到模型C下的温度分布：

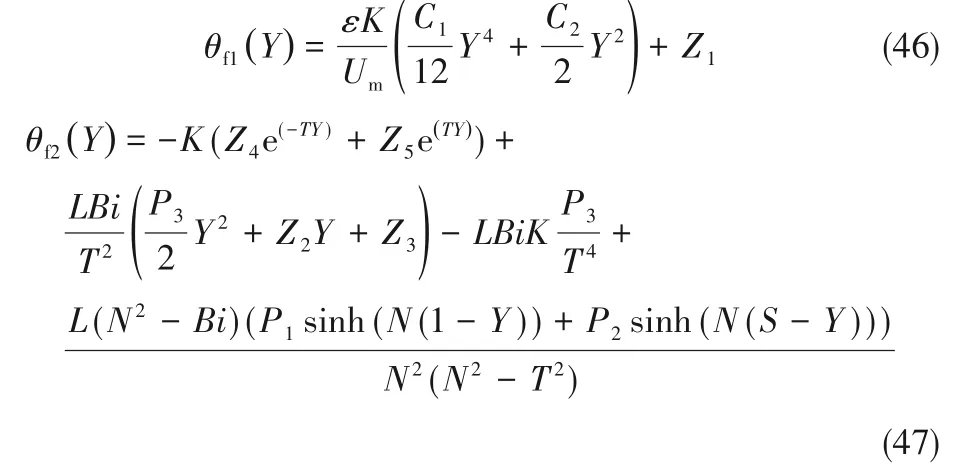
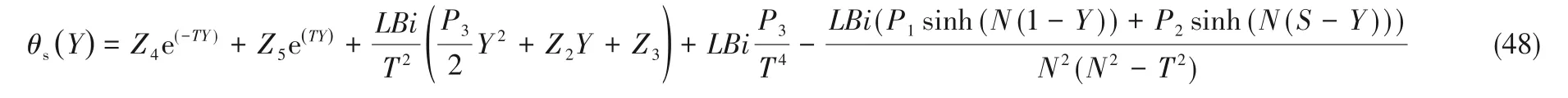
其中

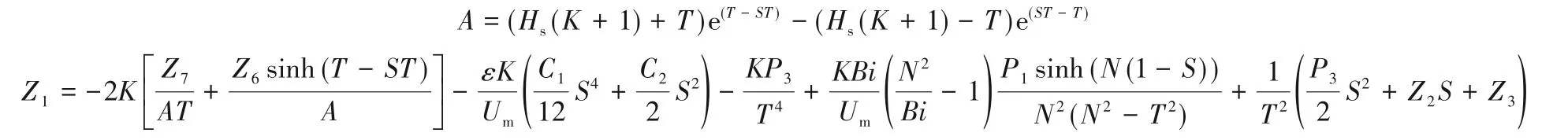
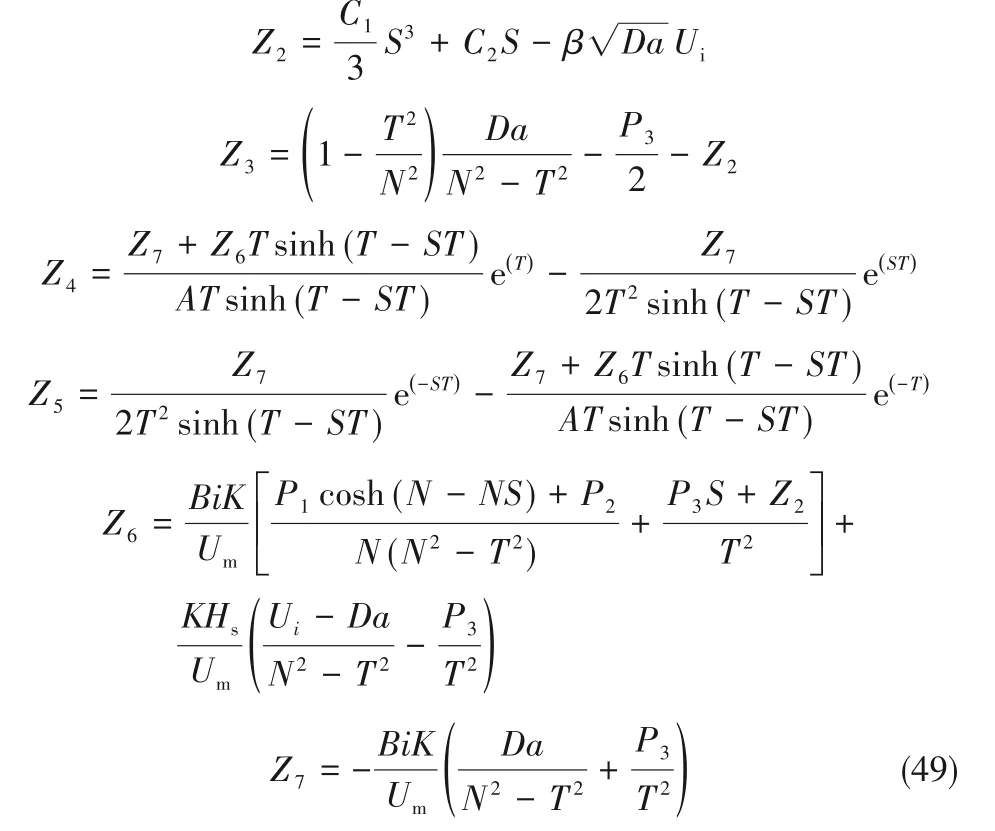
2.3 Nusselt数

部分填充多孔介质通道的Nusselt数Nu的计算公式为[29]：

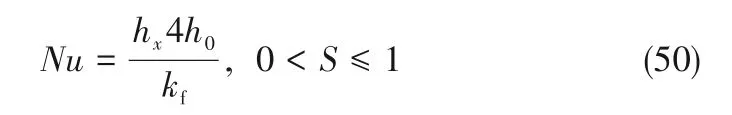
其中，hx是对流传热系数[30]：

将式（22）代入式（50）和式（51），Nu的无量纲表现形式为：

由式（40）可知：

因此Nu可写作：

其中，θm为通道平均温度：

2.4 平均温度

将所得流场精确解式（29）～式（33）及温度场精确解式（46）～式（49）代入式（55），则通道内流相的平均温度为：

其中

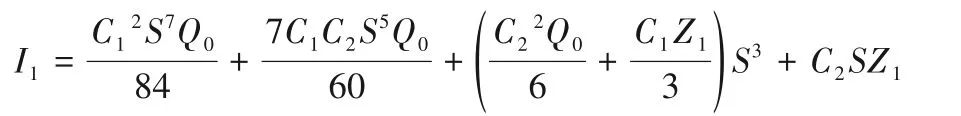
其中

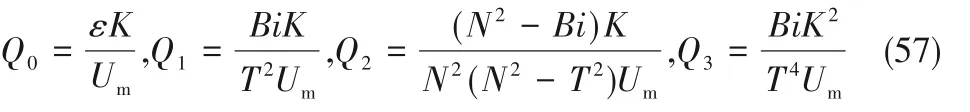
将式（56）、式（57）代入式（54）可以得到Nu的解析解。

3 解析解模型的验证

将本文计算得到的温度场解析解方程式（46）～式（49）与文献[22]中相同条件下的结果比较，结果见图2。发现在β=0，S=0.5，K=2，Bi=10，Da=10-3，ε=0.5的情况下，本文所计算的流相与固相温度的结果与Torabi等[22]所计算的两侧填充多孔介质平行板通道内流固两相温度分布的半解析解结果吻合良好。表1为Bi=10，Da=10-5，ε=0.9，Hs=1，S→0时，不同K下本文Nu计算结果与Yang等[12]计算的在完全填充多孔介质通道内Nu解析解结果对比。由于本文计算为部分填充通道，在近似计算完全填充多孔介质通道的Nu结果会产生一定误差，但误差很小。同时，根据式（54）～式（57），当S→1时，本文基于模型C预测的Nu为8.235，与无填充多孔介质的平行板通道内的流体传热Nu一致[29]。综上，证明了本文计算结果的正确性。

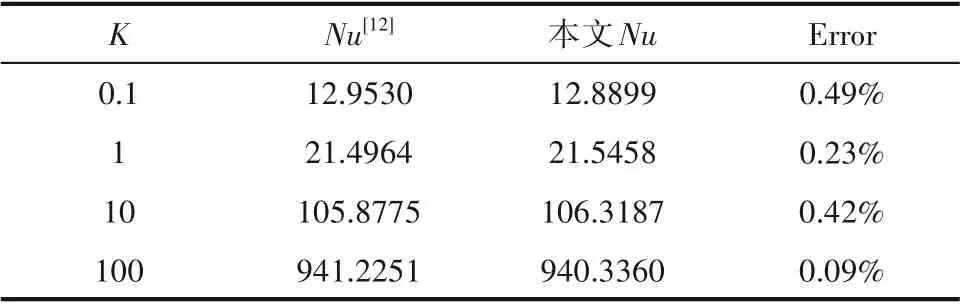
表1 在Bi=10，Da=10-5，ε=0.9，Hs=1，S→0时，本文与文献［12］Nu计算结果的对比Table 1 Comparison between the calculated results of Nu in this paper and those in Ref.［12］at Bi=10，Da=10-5，ε=0.9，Hs=1，S→0

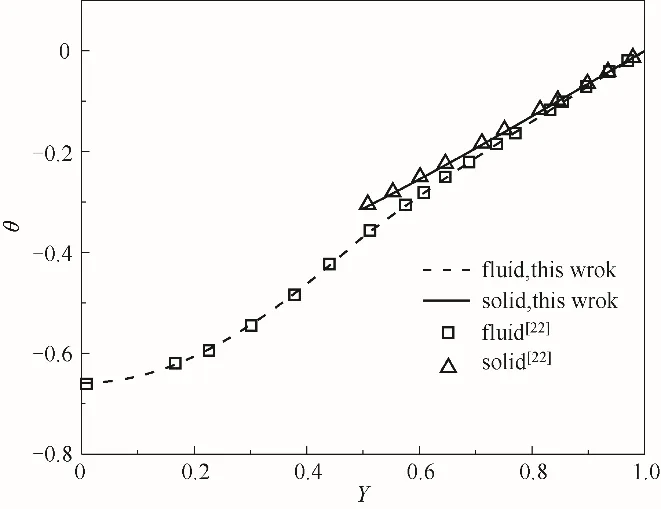
图2 在β=0，S=0.5，K=2，Bi=10，Da=10-3，ε=0.5时，本文温度场计算结果与文献[22]的比较Fig.2 The comparison between the calculated results of temperature field in this paper and Ref.[22]atβ=0，S=0.5，K=2，Bi=10，Da=10-3，ε=0.5

4 分析与讨论

4.1 不同参数对温度场的影响

图3所示为在固流两相热导率之比K=10，Biot数Bi=0.1，Darcy数Da=10-3，界面应力跳跃系数β=0时，不同空心率S下，界面对流传热系数Hs对通道温度分布的影响。由图3（a）可以看到在S=0.1，Hs=10.0时，多孔介质区内的流相温度先降低后升高，而固相温度则变化不大，导致多孔介质区接近中部位置处固相和流相温度之间出现最大温差。而随着Hs的减小，此最大温差所处的位置逐渐向界面处移动，如Hs=0.1时，多孔介质区内流固两相温差最大位置已发生在界面处，这是由于Hs较小时界面处流体和固体骨架之间的换热减弱。此外，随着Hs的减小，流固两相的温差逐渐增加，此规律也可以从图3（b）～（d）中看出。但在图3（c）、（d）中，即当S=0.5和0.9时，Hs取值0.1～10.0时，最大两相温差均发生在界面处，这是因为随着多孔介质填充厚度的减小即S增加，固相导热热阻减小造成固相温度逐渐接近壁面温度而流相温度也近似线性发展。在图3中，Hs为定值时，随着S的增加，自由流体区内流相温度逐渐减小；改变Hs时，流相温度变化比固相温度更明显。此外，Hs较大且S较大时，流固两相温差较小，这时可认为LTE模型在相应条件下有效。

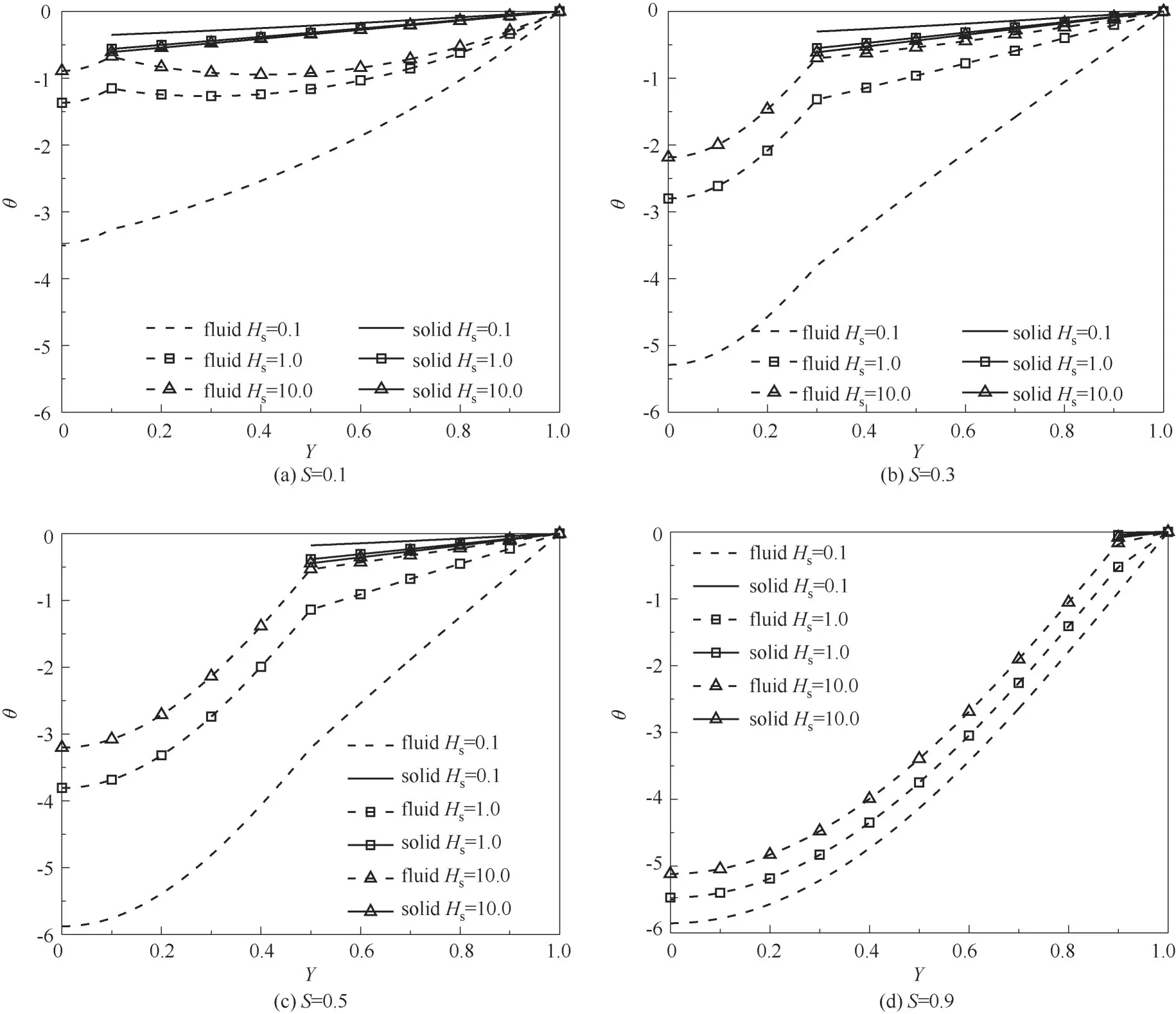
图3 在Da=10-3，K=10，Bi=0.1，β=0时，Hs对不同S下温度场的影响Fig.3 Effect of Hs on the temperature field in different S at Da=10-3,K=10,Bi=0.1 andβ=0

图4是在S=0.1，ε=0.9，β=0时，不同界面对流传热系数Hs，热导率之比K，Biot数Bi下的固相和流相温度场曲线。图4（a）中当K=0.1且Bi=0.1时，与图3（a）相比流固两相温度的变化范围明显减小，Hs的变化对温度场中流相温度的作用被削弱。而图4（b）中K=0.1且Bi=10，与图4（a）相比Bi增加，多孔介质区内流固两相间的换热增强，因此两相温差明显减小，且低Hs下的固相的温度曲线不再近似线性；而由于K较小两相温度变化的范围仍然较小，流固两相温差仍然较小。图4（c）中当K=10和Bi=10时，与图4（b）相比K增加，两相温度变化范围增加，且两相温度与K较小时的两相温度相比减小；与图3（a）相比Bi增加，流固两相之间的换热增加，使得在任何Hs下的两相温度的差距明显小于Bi较小时两种情况下两相温差，这种现象也可以在图3（a）、（b）的比较中看出。图4（d）中Da=10-5，与图3（a）相比Da减小，低Hs下两相温差增大，但是高Hs下的多孔介质区内两相温差减小。这与模型A不同[23]，使用模型C时，Da对两相温度的影响与Hs的取值有关。

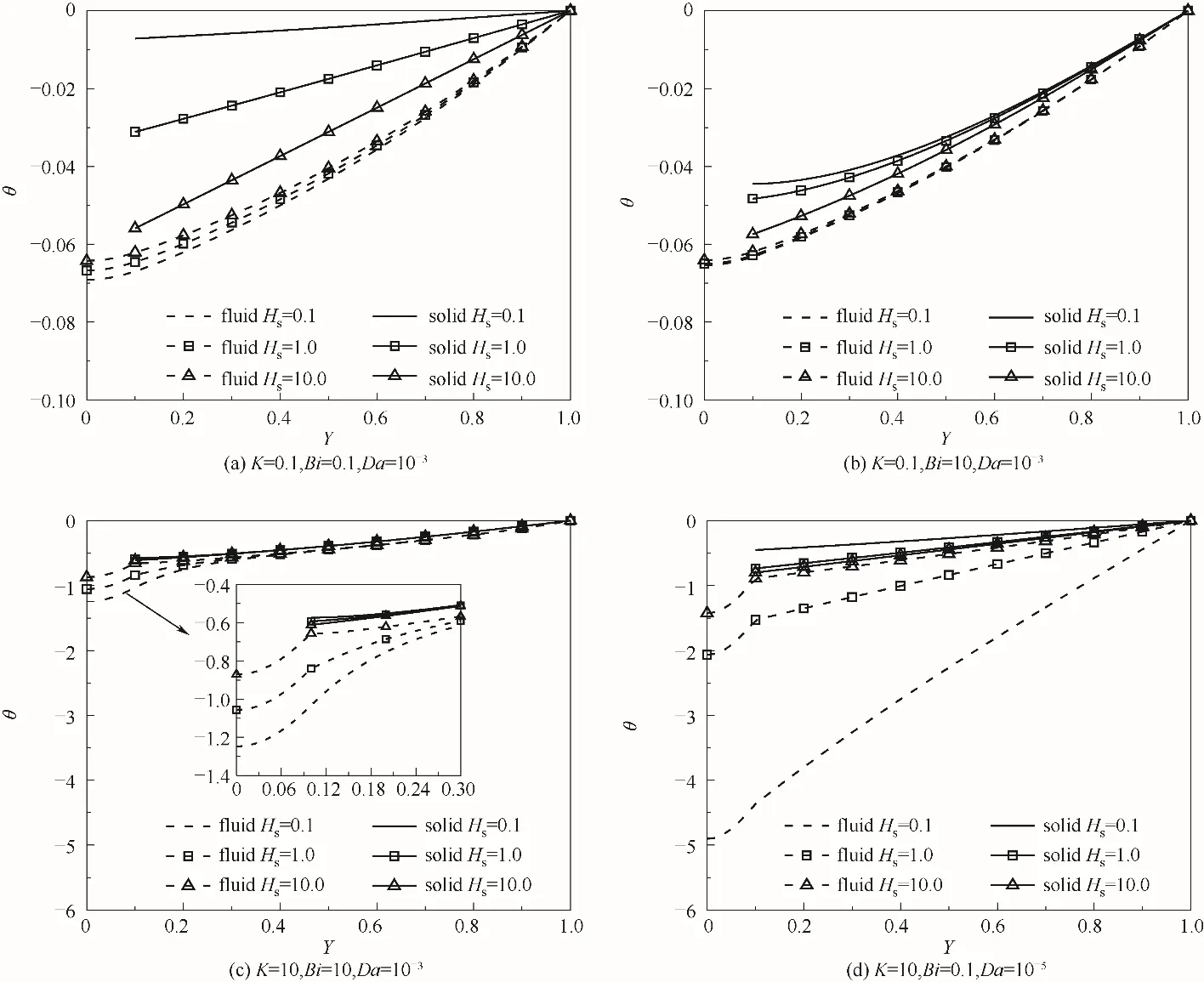
图4 在S=0.1，ε=0.9，β=0时，Hs对不同K，Bi和Da下温度场的影响Fig.4 Effect of Hs on the temperature field in different K,Bi and Da at S=0.1,ε=0.9 andβ=0

图5为在S=0.1，ε=0.9，Da=10-3，Hs=0.1时，不同K和Bi下，应力跳跃系数β对温度场的影响。在图5（a）中K=0.1和Bi=0.1时，β对固相温度的影响可以忽略，而随着β的增加流固两相温差逐渐减小，但总体来看由于K较小，流固两相温差仍然较小。在图5（b）中当K=0.1和Bi=10时，与图5（a）相比β对固相温度的影响增强，且此时Bi增加使流固两相温差进一步减小，且这一现象通过图5（c）、（d）也可以发现。此外随着β的增加，多孔介质区内流固两相温差逐渐减小，且减小的程度随着β的增加而降低。通过图5（c）、（d）与图5（a）、（b）对比也可以发现，K较大时，流固两相的温差较大，而在K较小时，流固两相温差则较小，且增大Bi可以进一步减小两相温差。

图5 在S=0.1，ε=0.9，Hs=0.1，Da=10-3时，不同K和Bi下β对温度场的影响Fig.5 Effect ofβon the temperature field in different K and Bi at S=0.1,ε=0.9,Hs=0.1 and Da=10-3

4.2 不同参数对Nu的影响

图6（a）中，在K较小时，如K<0.1时，Hs和K的变化对Nu的影响并不明显，但在K较大时，随K的增大Nu明显增加，且在K>1时，随Hs的增加Nu明显增加，这是由于在高K下，Hs对两相温度的影响较大。特别地，在低K区域S=0.3时的Nu小于S=0.1时的Nu，但S=0.9时的Nu明显要大于S=0.1时的Nu，因此Nu与S的关系并非单调的。对比图6（a）、（b）可以发现，增加Bi对低K区Nu的影响并不明显，这从图4与图3（a）的对比中也可以看到，在高K下Bi的变化对温度场的影响更明显；在高K区，不同Hs下的Nu之间差异明显减小，可以认为Bi的增加削弱了Hs对Nu的影响。为了进一步研究S与Nu之间的关系，得到了ε=0.9,β=0时不同K，Bi，Da和Hs下Nu随S的变化曲线，如图7所示。

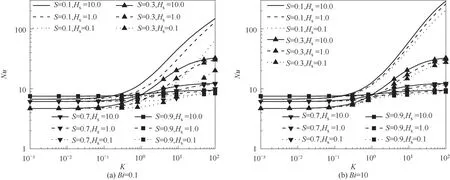
图6 Da=10-3，ε=0.9，β=0时，不同Bi，Hs及S下，Nusselt数与热导率比之间的关系Fig.6 Nusselt number versus effctive thermal conductivity ratio in different Bi,Hs and S at Da=10-3,ε=0.9,β=0

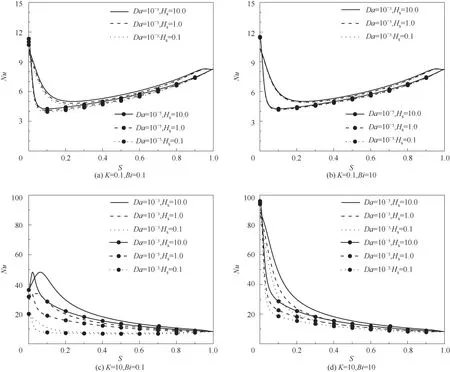
图7 在ε=0.9，β=0时，不同Hs，K，Da和Bi下Nusselt数与空心率（S>0）的关系Fig.7 Nusselt number versus hollow ratio（S>0）atε=0.9,β=0 with different values of Hs,K,Da and Bi

对于图7（a），K和Bi都为0.1，图中存在第一种曲线类型：Nu随着S增加先减小后增加，Da=10-3时，在S=0.2附近存在一个临界空心率Scr使得Nu最小；并且这个Scr在Da=10-5时会减小到0.05左右。同时Da减小时，低S下的Nu会随着S的增加加速下降，并且此时Nu最小值小于Da=10-3时Nu最小值。图7（b）中在K较小时的Nu曲线情况与图7（a）中的大致相同，Nu都较小，且在K较小时增加Bi对Nu影响可以忽略，这是因为K表示固相有效热导率与流相有效热导率之比，减小K意味着固相有效热导率降低，影响壁面热流传递到固相，降低整个通道内的传热效果，即使增强流固相之间对流传热效果也可忽略。但是由于Bi的增加，Hs对各种情况下Nu的影响被削弱，这与图3（a）与图4对比得到的结果一致。在图7（c）中，Nu与S的关系与图7（a）、（b）相比发生很大变化，在Hs=10.0和1.0时，呈现第二种曲线类型：当Da=10-3时，Nu会随着S的增加先增加后减小，在S=0.1附近存在Scr使得Nu最大，并且这个Scr会在Da=10-5时明显减小，而Da对Nu最大值的影响则并不明显，但Hs的减小却会明显减小通道内的Nu，且Nu与S之间的变化关系也因为Hs的变化发生变化。Hs=0.1时，可以看到Nu曲线呈现第三种曲线类型：Nu与S关系曲线中的极值点消失，曲线变为Nu随着S的增加单调降低。而这种单调曲线也呈现在图7（d）中的各种条件下的Nu曲线。Da=10-5与Da=10-3的情况相比，低S下的Nu会随着S的增加加速下降，即Nu对于较小的S更加敏感。图7（d）与图7（c）相比Bi增加，多孔介质区内流固两相换热增强，使整个通道Nu增加，各Hs下的Nu曲线的差距明显减小。基于模型C得到的Nu曲线与Li等[23]基于模型A得到的在相同条件下的Nu曲线对比发现，在Hs较大时，模型C与模型A的Nu随S变化曲线非常相似，当Hs继续增加时，模型C的Nu会无限接近于模型A的Nu但不会超越，并且具有相同的三种曲线类型，这是由于界面流固两相对流换热的存在使得界面处流固两相始终存在温差，因此模型C的Nu在数值上要小于模型A；而在Hs较小时，特别是在K较大Bi较小的情况下，两种模型的差异较大。总地来看，在K较小时，Hs对Nu的影响可以忽略，而在其他情况下，特别是K较大时，Hs对Nu的影响不可忽略，Nu会随着Hs的增加而增加，并且Hs的减小会减小Scr下的Nu最值。

为了讨论应力跳跃系数β对Nu的影响，图8给出了在ε=0.9，Hs=0.1时，不同β，K，Da和Bi下Nu与S的关系。在图8（a）中，K=0.1，Bi=0.1，Da=10-3且S<0.25时，可以看到Nu会随着β增加而增加，而S>0.25时Nu会随着β的增加而减小，整体来看β对Nu的影响程度会随着自身的增加而减弱。而在Da=10-5时，β对Nu的影响非常小，可以被忽略。图8（b）与图8（a）相比Bi增加，β对Nu的影响没有明显变化。而对于图8（c）、（d）而言，与图8（a）、（b）相比，K的增加提高了Nu，且在图8（d）中，Bi的增加进一步提高了Nu，使部分填充多孔介质通道传热增强，原因同图7。另外，图8（c）、（d）中，与图8（a）、（b）一样在S<0.25时，Nu随着β的增加而增加，且β对Nu的影响比S较大时的影响更加明显，而在S>0.25时，β对Nu的影响则可以忽略。总地来看，β的变化并不会改变Nu与S关系曲线的类型。对比图7和图8可以发现，K较小时（K=0.1），β对Nu的影响要大于Hs对Nu的影响，而K较大时（K=10），Hs对Nu的影响要明显强于β对Nu的影响。同时，Bi对Hs在Nu上作用的影响明显要强于其对β在Nu上作用的影响，且Da的减小会极大削弱β对Nu的影响。

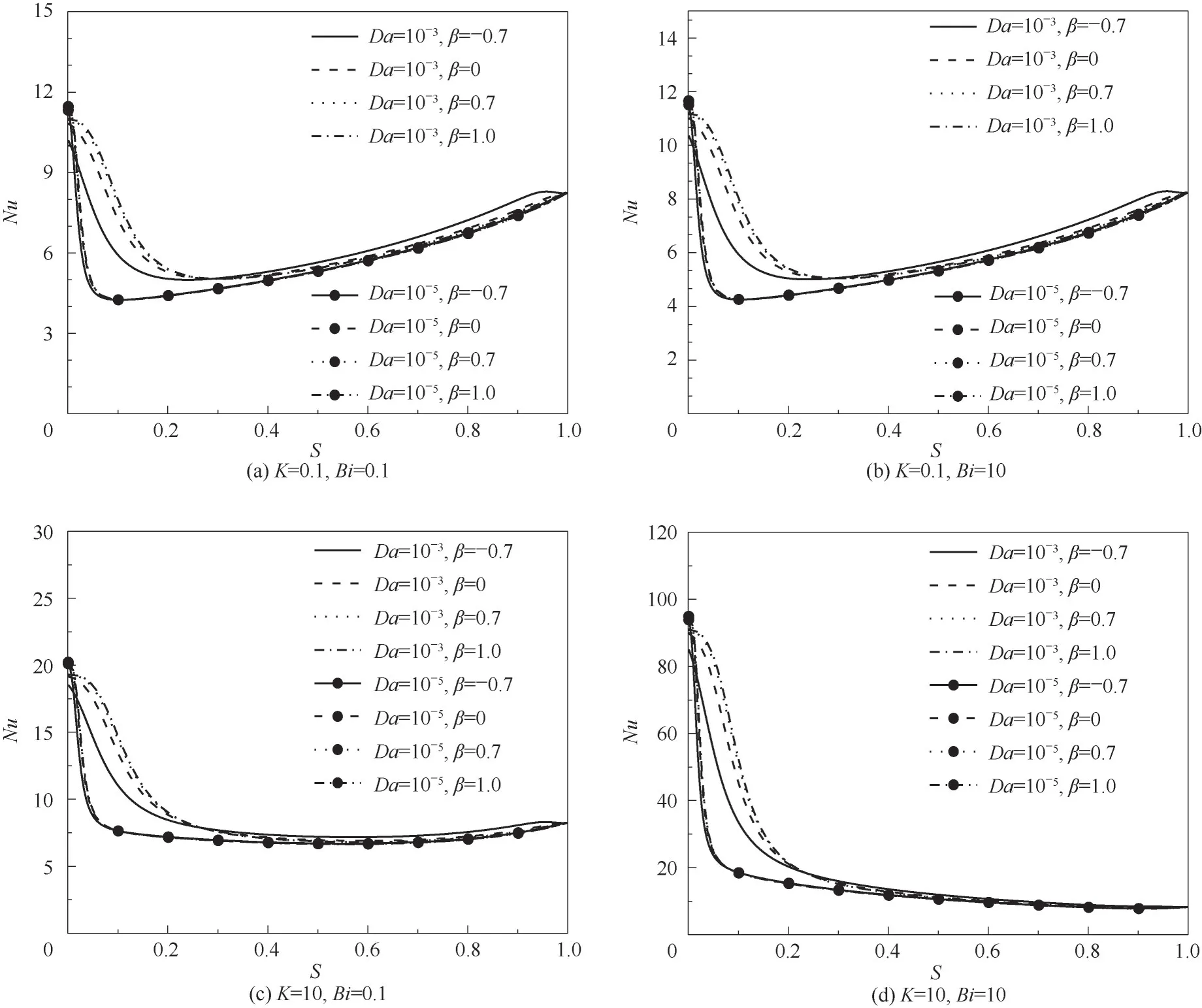
图8 在ε=0.9，Hs=0.1时，不同β，K，Da和Bi下Nusselt数与空心率（S>0）的关系Fig.8 Nusselt number versus hollow ratio（S>0）atε=0.9,Hs=0.1 with different values ofβ,K,Da and Bi

5 结 论

本文研究了上下壁面内侧填充多孔介质层平行板通道内的强制对流换热特性。通道壁面施以恒热流边界条件。在多孔介质区内采用Brinkmanextended Darcy模型和LTNE模型为运动及能量方程，并采用应力跳跃条件和模型C为其界面条件。得到了通道内流相与固相温度以及Nusselt数的精确解析解，并在此基础上分析和研究了界面对流传热系数Hs、应力跳跃系数β、空心率S、固流两相热导率之比K、Darcy数Da以及Biot数Bi等对通道内流体传热效果的影响，得到如下结论。

(1)Hs较小时，β和Da的增加会减小两相温差。而在高Hs下，Da减小也会减小两相温差，这与模型A下计算得到的结果一致[23]。

(2)Da，K和Hs较大且Bi和S较小时，流固两相间会在接近多孔介质区中部出现最大温差，而该最大温差会随着S增加和Da及Hs的减小向界面区移动。

(3)对于不同K（K=0.1，10）与Bi（Bi=0.1，10），Nu与S的关系曲线存在不同的类型，与模型A不同的是，模型C的Nu曲线类型与Hs有关。Hs较大时，模型C的Nu曲线类型与模型A下的结果相似，有三种类型：存在Nu最小值，存在Nu最大值以及Nu随S增加单调递减；而Hs较小时，有两种类型：存在Nu最小值以及Nu随S增加单调递减。且总体而言，模型C下的Nu要小于相同条件下模型A下的Nu，增大Hs会使模型C的Nu逐渐接近模型A的Nu但不会超越。

（4）在K较小时（K=0.1），β对Nu的影响要大于Hs对Nu的影响，Hs对Nu的影响则可以忽略，并且β在较小时与应力连续界面的Nu稍有区别；而在K较大时（K=10），Hs对Nu的影响要远大于β对Nu的影响，且Hs增加会明显提高通道内流体传热强度Nu。

符号说明

asf——多孔介质区流相与固相之间接触的单位面积，m-1

Bi——Biot数

cp——流体的比定压热容，J·kg-1·K-1

Da——Darcy数

f——摩擦系数

G——x方向压力梯度

Hs——无量纲界面对流传热系数

hf,h0——分别为自由流体区的一半高度和通道一半高度，m

hsf,hi,s——分别为多孔介质区内孔隙对流传热系数和界面对流传热系数，W·m-2·K-1

hx——局部传热系数，W·m-2·K-1

k——多孔介质渗透率，m2

kef,kes,kf——分别为多孔介质区流相有效热导率，多孔介质区固相有效热导率和自由流体区液相热导率，W·m-1·K-1

Nu——Nusselt数

p——压力，Pa

q——热流量，W·m-2

S——通道空心率

t——温度，K

U——无量纲速度

u——速度，m·s-1

x——径向坐标，m

Y——y方向无量纲坐标

y——纵坐标，m

β——界面应力跳跃系数

γ——界面热流与壁面热流之比

ε——多孔介质孔隙率

θ——无量纲温度

μ——动力黏度，kg·m-1·s-1

ρ——流体密度，kg·m-3

下角标

eff——有效参数

f——流体

f1——自由流体区流相

f2——多孔介质区流相

i——界面

m——平均

p——多孔介质

s——多孔介质区固相

w——壁面