壁面脉动传热对气波制冷性能影响研究

刘庭江，王静娴，于洋，赵一鸣，胡大鹏

（1大连理工大学化工学院，辽宁大连 116024；2大连工业大学机械工程与自动化学院，辽宁大连 116034）

引 言

气波制冷技术[1-8]是一种通过压缩波和膨胀波等压力波的交互作用实现冷热分离的新型膨胀制冷技术。双开口气波制冷机凭借体积小、转速低、可带液运行、有利于能量回收等特点，成为气波制冷机发展的主流，拥有广泛的应用前景。其核心工作部件为一系列周向排列的振荡管组成的管束，振荡管束两侧布置高压进气喷嘴、高温出气喷嘴、常压回气腔与低温排气腔[9-11]。振荡管通过旋转与喷嘴、腔体周期性接通，从而产生压力波实现制冷。目前，已成功研发出外循环耗散式气波制冷技术[12-14]，随后基于降低循环系统损失思想，研发出过膨胀气波制冷技术[15-17]和二次增压气波制冷技术[18-20]。

双开口气波制冷机作为一种典型的流体机械，振荡管内气体发生对流换热是不可避免的，是造成气波制冷等熵膨胀损失的重要因素之一。特别对于低流量小型气波设备来说，边界效应显著，导致制冷效率急剧下降。振荡管内非定常对流换热行为会造成振荡管温度呈不均匀分布状态[21-24]，此时必然存在导热现象。振荡管内导热与对流换热是相互影响的，通过合理控制振荡管导热程度可以弱化对流换热强度，提高气波制冷性能。

Welch等[25]、Paxson等[26]、Elloye等[27]先后通过理论分析、Colburn经典传热模型、一维非稳态耦合传热模型，对气波压力交换机中壁面传热导致的能量损失进行研究。Li[28]建立恒壁温数值模型，对气波增压设备热边界层效应进行研究；Deng等[29]建立单通道热流耦合三维模型，研究微型波转子增压性能受对流换热的影响。上述研究对象均为气波增压设备，与气波制冷设备工作环境和工作过程存在较大差异，且制冷关注于壁面传热造成的冷量损失，与增压设备研究目标不同。同时，以上研究振荡管壁面温度均采用恒温条件，但对于绝大多数气波设备来说，振荡管束作为旋转部件，获取其温度分布数据存在难度。

为了研究双开口振荡管壁面传热对制冷性能的影响，本文在振荡管束静止、两端喷嘴周期旋转的双开口气波制冷实验设备基础上[30]，搭建多点温度测量实验平台，对振荡管壁面温度进行测量。通过不同厚度振荡管温度测量结果，分析温度分布特征和导热的关系。基于温度分布特征建立数值传热模型，对振荡管内流体与固壁间对流换热行为规律进行研究，分析对流换热对制冷性能的影响。最终，通过对不同壁厚振荡管束进行制冷性能实验，验证壁面导热对制冷性能的影响。该研究为双开口气波制冷优化设计提供理论与实验基础，对于提升设备自身制冷深度具有重要意义。

1 气波制冷实验平台

1.1 实验装置及流程

为了方便对温度进行测量，实验装置为振荡管束静止、两端喷嘴周期旋转的双开口气波制冷机[30]。气波制冷实验流程如图1所示，实验介质为空气。为获得稳定气源，高压气体由螺杆式压缩机与储气罐共同提供。高压气体在气波制冷机内与常压气体进行换热作用，排出低温气体，同时常压气体被加热为高温气体排出。排出的高温气体经过换热器重新降温为常压气体进行循环。在管道上布置仪表监测进出口温度与压力，压力表精度等级为0.4级，温度传感器为Pt100热电阻传感器。实验现场图如图2所示。设备主要参数如表1所示。

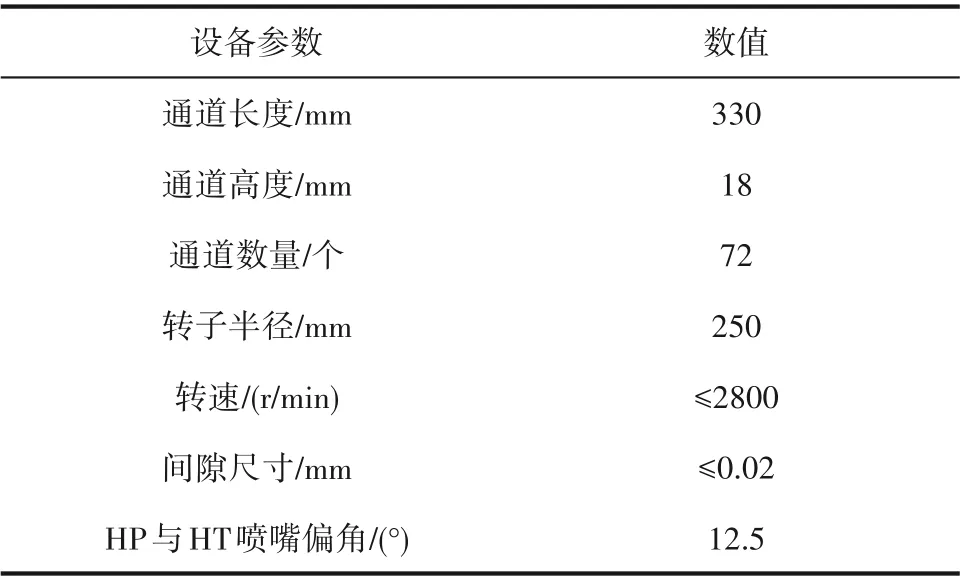
表1 设备设计参数Table 1 Design specifications

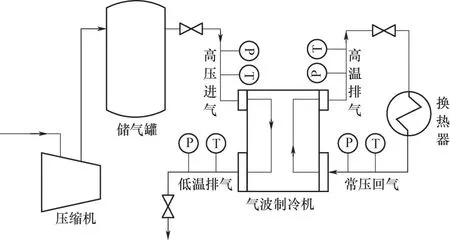
图1 实验流程示意图Fig.1 Schematic diagramof the experimental process

图2 实验装置现场图Fig.2 Field diagram of experimental device

1.2 温度测量系统

温度测量系统包括27个薄膜电阻（Pt100）和32通道巡检仪，本实验采用的薄膜电阻的探头尺寸为2.1 mm×2.3 mm×0.9 mm，精度0.3%FS，测温范围-70～100℃。巡检仪是上海驰控有限公司的XMD-32型32路智能多路温度巡检仪，最多同时采集32个温度值，数值采集精度0.2%FS。为了降低系统的随机误差，每个温度测量的最终值采用五次连续测量的平均值。

1.3 阶梯振荡管束壁面

为了研究轴向导热面积对壁面温度分布的影响。将振荡管束外壁面加工为厚度10 mm、8 mm、6 mm三个区域，如图3所示。每个区域对应7根气波管束，以降低不同区域之间的影响。在每一区域沿轴向均布9个温度传感器，对三个不同区域的壁面温度进行同步采集。实验过程中，气波管束内壁及外壁表面均覆盖有陶瓷纤维绝缘材料，以排除外界环境的干扰。薄膜电阻由具有良好导热性能的硅橡胶材料，固定在气波管束外边面上。

图3 不同壁厚气波管束Fig.3 Gas-wave tube bundles with different wall thicknesses

2 非定常流动数值计算方法

2.1 数值计算模型

数值计算中所涉及的气体被假设为可压缩理想气体。基于密度的求解器，满足质量守恒定律、动量守恒定律和能量守恒定律。湍流模型采用增强壁面处理的低Reynolds数Realizablek-ε模型，低Reynolds数法在近壁区分布网格，对近壁区与湍流核心区分别求解，能有效解决流体边界对流换热的传热问题。为准确捕捉管内各类波及间断，采用AUSM离散格式。

2.2 网格划分与无关性验证

振荡管束沿轴向展开，简化为二维计算模型进行计算[20]。计算区域包括气波管流道（tubes）、高压口（HP）、高温口（HT）、低温口（LT）、常压回气口（MP）和两侧间隙。气波管区域与各端口间采用滑移网格；HP、HT、LT设置为压力进出口，MP采用流量入口，其流量值采用udf（user defined functions）定义为与HT出口流量相等。由于壁面温度稳定时间过长，一个制冷周期内的流体与管壁间发生的非稳态热量传递不足以使壁面产生明显的温度变化，振荡管壁面赋值基于实验所得振荡管轴向坐标的温度函数。并进行边界层网格划分，如图4所示。振荡管上下近壁流体域第一层网格厚度为1.5×10-3mm，计算过程中基本保证了尺寸网格满足y+≈1的条件。为了使计算更容易收敛，在进出气腔与气波管相通侧及气波管两开口端也进行了一定的网格加密。该模型具有82.8万网格。

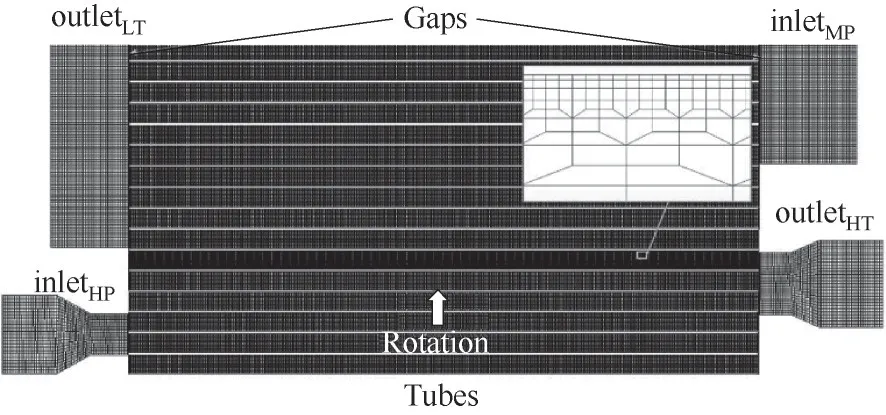
图4 传热数值计算物理模型及其网格划分Fig.4 Physical model and meshing of heat transfer numerical calculation

固体壁面与实验设备一致为碳钢材料，比热容取460 J/(kg·K)，热导率取46 W/(m·K)。本次数值计算主要求解振荡管内流体与管壁之间的对流换热量。流固间对流换热行为发生在紧邻壁面的计算单元内。若紧邻壁面网格节点P在近壁区内，流动处于层流状态，若壁面温度为Tw，从壁面传递到近壁网格的热量为

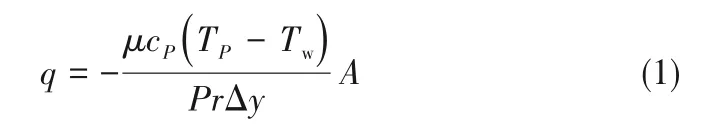
其中，TP是流体的温度；Pr是流体的Prandtl数；Δy是近壁节点P到固壁的距离；A是节点对应控制体积在壁面处的面积。

从经济角度分析，需在满足计算精度的条件下，尽量增大网格尺寸与时间步长来降低计算成本。建立局部计算模型，每隔1×10-5s提取壁面对流换热量，进行网格无关性与时间步长无关性验证。结果如表2所示。当时间步长由1×10-7s减小到1×10-8s，第一层边界层高度由0.0015 mm减小到0.0010 mm时，计算结果无显著性差异。

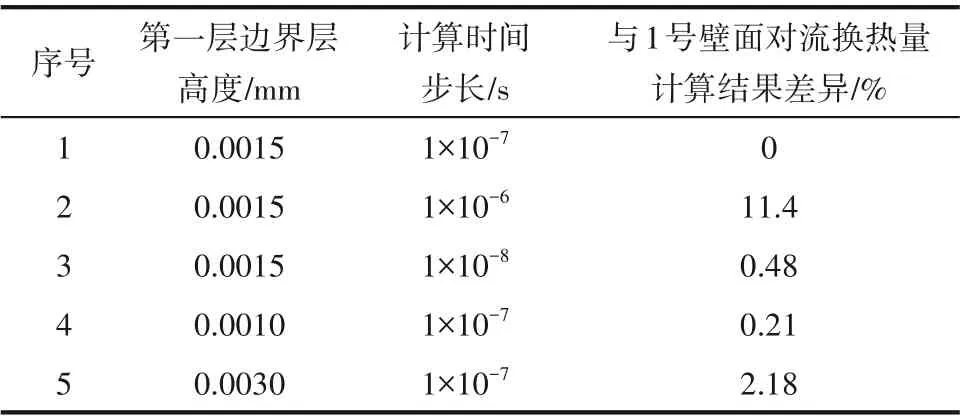
表2 网格与时间步长无关性验证Table 2 Grid and time step independence test

2.3 数值传热模型验证

本文的数值传热模型通过Ozawa激波管实验进行验证。激波管内部气体发生的运动行为与气波制冷过程有相似性，均是运用非定常波系实现能量传递的非稳态流动过程；且激波管内气体运动温差大，易于实验数据的获得。Ozawa[31]通过高速摄像技术对激波传递过程中的壁面温度进行测量，利用高频热电偶采集振荡管温度变化。实验驱动气体压力550 kPa，温度293 K；被驱动气体压力5 kPa，温度293 K。对实验中x0测量点的传热行为进行对比计算，所得壁面温度与热通量结果如图5所示。

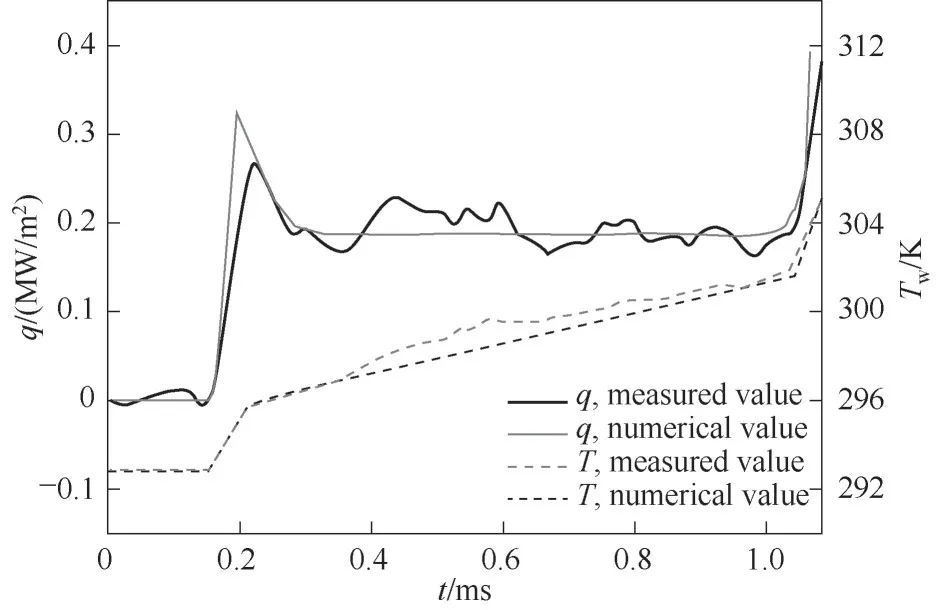
图5 热通量和壁温实验与计算结果Fig.5 Experimental and numerical calculation results of heat flux and wall temperature

图中虚线为Ozawa激波管实验中测量点的热通量和壁面温度实验结果。把温度实测曲线线性拟合，拟合结果作为数值计算中流体域壁面的边界条件。对比发现，热通量变化趋势整体一致，由于在数值计算中，将实验测得的壁面温度进行了近似线性处理，使得计算的热通量相比实验值较为平稳。第一道激波约在0.12 ms时到达测量点，因固壁反射发生的反射激波约在0.8 ms时到达测量点，在激波与反射激波经过测量点均有能量激增，实验测量中激波到达测量点时间约比数值计算值滞后0.03 ms，主要原因为温度测量本质是热量的积累，所以会稍显滞后。说明该模型可以较准确模拟非稳态流动的固壁传热。

3 结果与讨论

3.1 壁面温度分布实验

膨胀制冷过程由高压进气与低温排气阶段构成，类似于膨胀机。将膨胀前后压力的比值定义为膨胀压比α

将膨胀前后温度的差值定义为制冷深度ΔT

在3种不同膨胀比的工况条件下，对不同厚度振荡管进行壁面温度测量实验。稳定后不同工况高温进气温度、低温排气温度以及壁面温度分布如表3与图6所示。实验研究发现，高温端口侧壁面温度逐渐升高，低温腔侧温度逐渐降低，壁面温度形成最终稳定的不均匀分布约需要90 min，经历数十万个制冷周期，远大于一个制冷周期所用时间。相同10 mm壁厚下在不同工况下，膨胀比由小至大制冷深度分别为11.9、17.7、20.0 K；对应壁面温度变化分别为10.0、19.3、26.0 K。由实验结果可知，膨胀比越大，气体制冷深度越大，温度变化越明显，相应管束壁面沿轴向温度分布不均匀程度越大。以膨胀比1.8工况为例，不同壁厚壁面由厚至薄温度变化分别为19.3、20.4、21.7 K，且高温端温度上升，低温端温度下降。

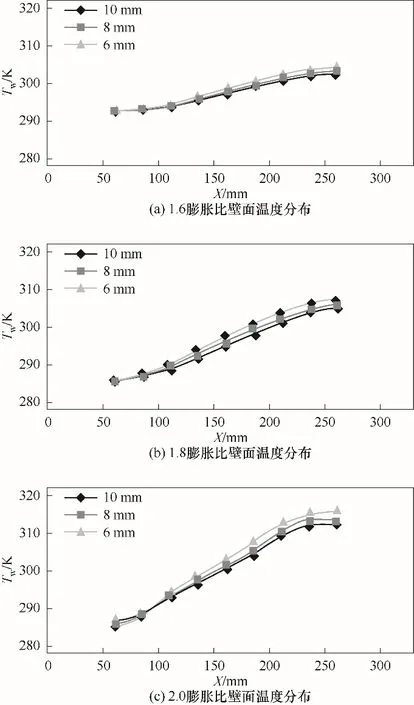
图6 不同壁面厚度轴向温度Fig.6 Axial temperature of gas-wave tube under different wall thickness

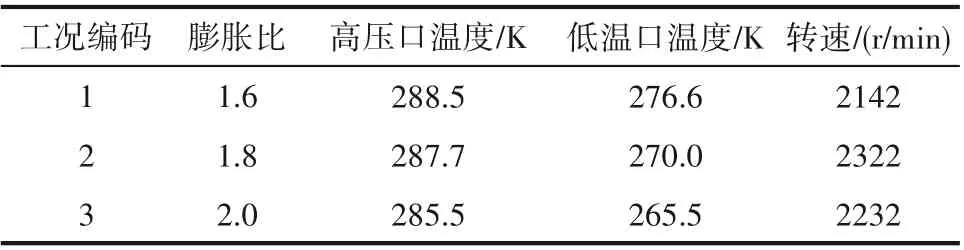
表3 壁面温度测量实验工况Table 3 Experimental conditions for temperature measurement

由于壁面温度变化并不均匀，计算其具体轴向导热量值。导热量计算以靠近高压端口的测量点为起始数据点，计算不同壁厚下后一个数据点到前一个数据点的轴向导热量。所得导热值如图7所示。由图可知，轴向导热主要发生在中间区域，在接近振荡管束的正中间位置，距冷端热端较远且管内主要为中压常温气体，壁面温度变化相对平缓，轴向导热量减小。随着壁面厚度减薄，振荡管束的轴向导热量减少。说明外壁面厚度越薄，轴向导热面积越小，导热量越小，壁面轴向温度分布越陡峭。

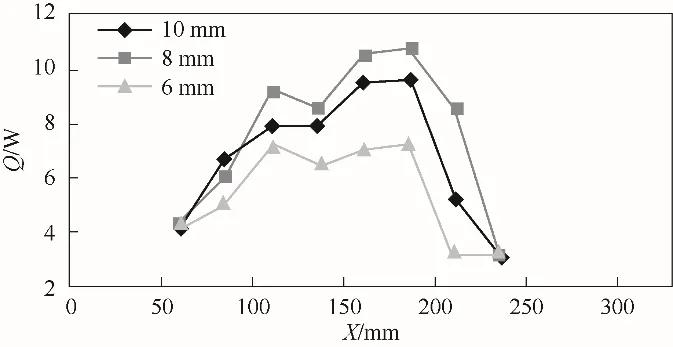
图7 工况2下轴向导热量Fig.7 Axial heat conduction under working condition 2

3.2 对流换热数值分析

由3.1节分析可知，由于轴向导热的影响，会形成不同的壁面温度分布。而在对流换热中，流固接触的固体壁面温度分布是影响对流换热量的重要因素，能够直接影响最终的制冷效率。采用数值分析的方法，以膨胀比1.8工况为例，将3.1节实验所得10 mm厚度壁面温度实测结果进行拟合，作为数值计算中流体域壁面边界条件。所得流体温度分布以及与壁面对流换热热流量云图如图8所示。

计算由高压进气开始，至低温开始排气结束。为直观展示温度与对流换热量。温度值与对流换热量值x轴沿振荡管轴向位置展开，y轴沿时间展开。图8(b)负值为气体对振荡管放热，正值为气体从振荡管吸热。气体在振荡管内进行周期性非定常流动。振荡管吸热主要发生在高压射气阶段，因为该阶段管内气体经过激波的作用温度与速度突升，加强了与壁面的对流换热，且气体温度高于壁面温度，释放出热量；振荡管放热主要发生在低温排气阶段，在该阶段中通过膨胀波的反复作用，高压气体膨胀为低温气体。振荡管温度高于管内气体温度，对气体放热，气体吸收热量约为19.7 W，计算读取低温排气流量为0.2 kg/s，该热量会使气体温度升高1.96 K，在整机模型中，低温区域远大于计算中的低温区，对流换热对低温气体的影响将更为严重。

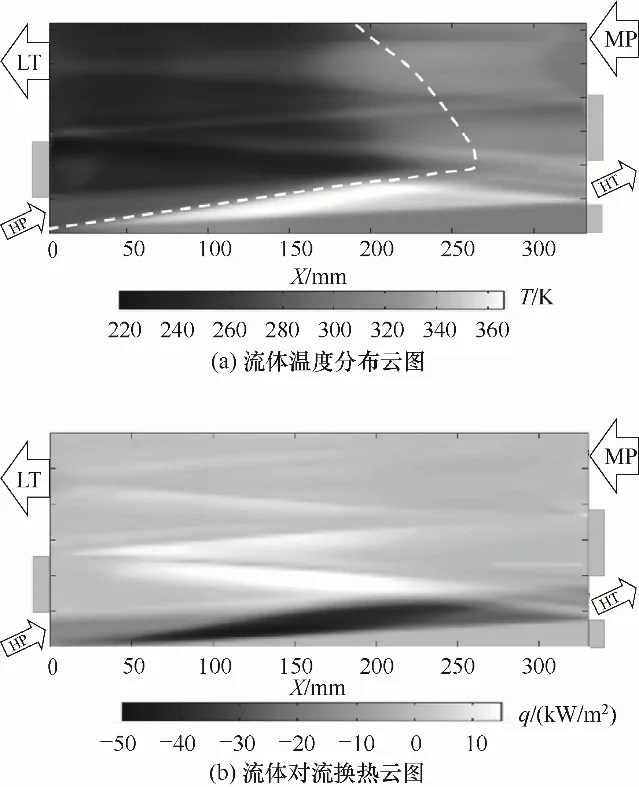
图8 温度与对流换热云图Fig.8 Temperature and convective heat transfer nephogram

因此可知，低温排气阶段管壁与管内流体的对流换热会降低设备制冷效率。由3.1节分析可知，壁面厚度增加，会增加管束轴向导热量，使冷端壁面温度增加。冷端壁面温度越高，壁面与冷气的对流换热行为越剧烈，换热量越大，冷量损失越严重。应尽量减小轴向导热面积以降低冷端的壁面温度。

3.3 不同厚度振荡管制冷深度实验研究

由以上分析可知，振荡管壁面换热是一个复杂的过程，振荡管束能通过其本身的轴向导热改变其轴向温度分布，进而通过对流换热影响设备的制冷深度。为验证该分析，将气波管束壁面厚度整体从10 mm减薄至5 mm。实验中管束内、外壁面均进行绝热处理。设备结构尺寸不变，对比对壁厚减薄前后设备的制冷性能。得到种不同工况下制冷深度随转速变化如图9所示。最大制冷深度ΔT如表4所示。由图可知，随着转速增加，制冷深度先增大后减小，存在最佳转速使得制冷深度达到最大。在三个工况下的制冷深度均提升，最大制冷深度增加了0.2、0.5和0.4 K。因此可知，振荡管耦合换热会对设备的制冷效率产生影响，减小振荡管的轴向面积，能够有效提升设备的制冷效率。

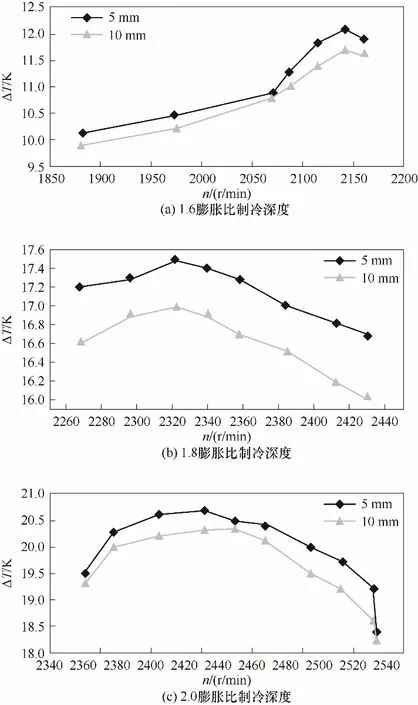
图9 不同转速制冷深度Fig.9 Refrigeration depth at different rotating speeds

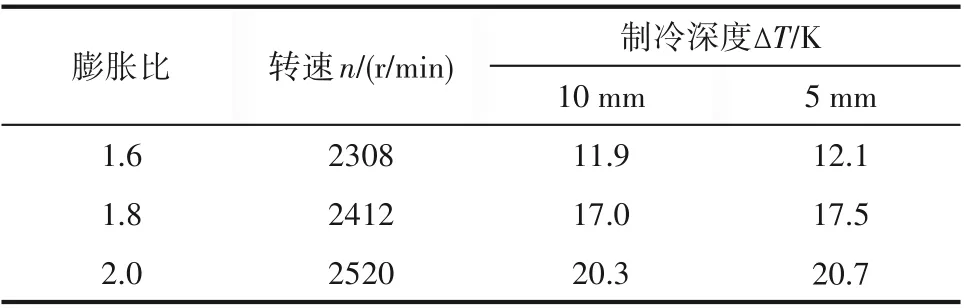
表4 不同壁厚制冷深度Table 4 The refrigeration depth with defferent thickness

4 结 论

（1）壁面温度稳定时间远大于一个制冷周期的时间，壁面温度变化最终会达到稳定状态，稳定后振荡管束壁面会形成沿轴向不均匀温度分布。振荡管束的轴向导热会影响最终壁面温度的分布，轴向导热面积越小，轴向导热量越小，温度分布越陡峭，不均匀程度越大。

（2）振荡管束与管内流体对流换热会导致低温气体温度升高，直接造成制冷深度损失。以1.8膨胀比计算结果为例，管壁对气体放热19.7 W，从而造成制冷深度下降了1.96 K。低温侧壁面温度越高，冷量损失越严重，制冷深度越小。

（3）经过不同壁厚对比实验验证，在三种膨胀比工况下，5 mm壁厚实验相较于10 mm壁厚实验最大制冷深度提升了0.2、0.5、0.4 K。说明减小管束轴向面积能够削弱壁面脉动传热，提升制冷效率，进而验证了脉动壁面传热对制冷性能的影响。