波利亚“怎样解题”理论指导下的一次教学实践

胡宇

摘要：培养学生解题能力是数学教育的核心，也是贯穿于教学始终的一项基本任务。本文以一道经典的“线段和的最小值问题”为例，展示了波利亚“怎样解题”理论中“弄清问题、拟订计划、实现计划、回顾反思”四个步骤。从核心素养培养的视角来看，在数学教学中贯彻波利亚“怎样解题”理论，有助于学生学会用数学的眼光发现问题并提出问题，用数学的思维分析问题，用数学的语言表达问题并解决问题，从而进一步理解其数学本质。

关键词：弄清问题  拟订计划  实现计划  回顾反思

解题即解决问题，是数学教学活动的核心。波利亚“怎样解题”理论把解题过程分成四个步骤，即弄清问题、拟订计划、实现计划、回顾反思，每一个步骤分别由多个具体的子部分组成。这一理论注重引导学生首先弄清问题，分析条件和结论，接着拟订计划，探索条件和结论之间的联系，最后实现计划，及时回顾反思，并尝试改变条件或结论，将问题推广，从而使学生进一步理解其数学本质。

笔者结合校内教研课例《线段和的最小值问题》，基于波利亚“怎样解题”理论指导下的一次初中数学课堂教学实践活动，谈一谈自己的一些思考。

一、问题呈现

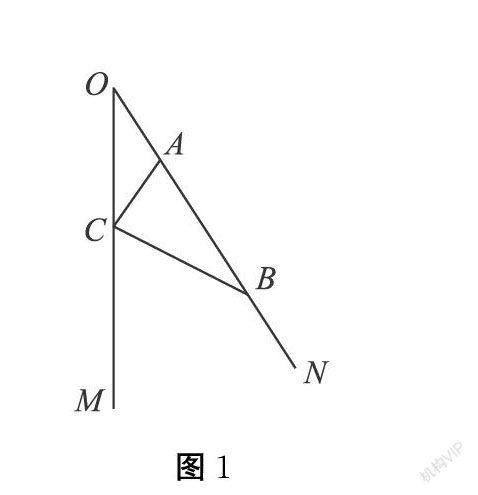
如图1，∠MON=30°，点A，C分别是边ON，OM上的动点，点B在ON上，OB=2，求AC+BC的最小值。

本题属于平面几何中线段和的最小值问题，对于初中生来说是棘手问题之一，也是中考数学命题热点之一。此类问题经常出现于各省市中考试题中，出题主要有角、三角形、四边形、圆、函数等，基本解题思路是：注意观察动点的运动规律或存在的特殊位置，可以先把一个动点看作定点，化“动”为“静”;然后找出定点关于直线的对称点，通过对称化“折”为“直”，化“散”为“集”;再与勾股定理联系在一起，求出线段的长;依据垂线段最短，进而得到线段和的最小值。

二、教学实录

活动1 弄清问题

师：题目已知什么，求什么？

生1：已知∠MON=30°，点A、点C是动点，OB=2。

生2：求AC+BC的最小值。

师：求线段的最小值，也就是最值问题，以前我们有过这样的解题经历吗？是利用什么解决的？

生1：两点之间线段最短。

生2：垂线段最短。

生2：利用最短路径求解，如图2所示。

活动2 拟订计划

师：我们进行怎样的转化，利用它们就能求出AC+BC的最小值呢？

师：点A、点C都是动点，可不可以先把一个点固定，让另一个点为动点？

生1：固定点C。

生2：固定点A。

学生思考，分小组合作、交流，制订解决方案，教师巡视指导。

活动3 实现计划

生：固定点C，如图3所示。

师：此时BC长固定，要使AC+BC的值最小，需要AC长最小即可，怎么办？

生：过点C作ON的垂线段CA。

师：按照这个思路，C点變化，BC+AC的值也发生变化吗？

生1：变化。

生2：BC与OM垂直时，AC+BC的值最小。

师：这种情况下AC+BC的值最小吗？

生：不一定。

师：下面，我们换另一个点A，再试着思考。

生1：固定点A，如图4所示。

生2：转化为最短路径问题了。

师：我们现在可以解决问题吗？

生：作A点关于直线OM的对称点A′，连接BA′，与OM交于C点，连接AC，AC+BC的值最小。

师：A点其实是一个动点，这种做法能不能进行改进？

生：作B点关于直线OM的对称点就可以了。

师：是的，如图4右图，AC+BC的值就是B′A的长。想一想什么情况下它的值最小。

生：B′A与OB垂直时最小。

师：你能算出这个值吗？

生：利用勾股定理，可得3。

活动4 回顾反思

师：请重新叙述题目已知什么和求什么，是怎样计算出结果的。

生：……

师：本节课，我们学习了哪些数学知识和数学思想方法？

生1：利用数学基本事实和最短路径模型求出线段和的最小值。

生2：转化思想、模型思想。

师：把这个问题进行变形，能不能求出BC+AB或AC+BC+AB的最小值？同学们接着进行思考和总结。

生：……

三、几点思考

（一）以生为本，注重探究

对于当前的基础教育，专家强调：教师要立足教材，还原课堂的本色，展现学生的个性，关注学生人格的养成，让学生充分发挥自己的主动性和能动性。可见，我们的课堂教学应该回归本真，力求简洁和实效。本节课仅安排了一个主要问题，充分诠释了这一理念。教师开门见山地出示问题，以问题为载体，从学生已经掌握的数学知识和经验出发，引导学生从待求问题联想到最短路径几何模型，运用数学公理“两点之间线段最短”和“垂线段最短”，依据模型化动为静，再联系勾股定理求出线段的长，从而得到线段和的最小值。在“分析问题”教学过程中，学生结合已经掌握的数学知识和经验、思维和灵感参与课堂活动全过程，尝试画一画、议一议、做一做。教师引导每一位学生动脑、动手、动口，进行展示与交流。一系列的探究交流活动，让学生主动思考与讨论，交流收获与体会，逐步感悟数学思想方法，积累数学活动经验。

（二）经历过程，关注生成

“生成”是课程改革倡导的一个重要的教学理念。数学教师的任务不仅仅是教给学生数学知识，更重要的是培养学生的思维能力，使其感悟数学知识的生成过程，让枯燥的数学知识变得鲜活。本节课教师首先引导学生明确题目已知什么、待求什么，让学生养成“聚焦”“标注”关键条件的审题习惯。然后让学生分组合作、交流讨论，拟订解决方案。教师引导学生明确解题思路，根据“有什么”，确定“要什么”，把握“做什么”。接着学生实行计划，给出解题过程，若过程中出错或思维受阻，及时进行方案或计划的调整，并检验每一步保证都正确，直到问题解决。最后学生回顾反思，从知识、思想、方法、基本模型、解题策略等角度进行总结，明确问题本质，并思考其他解法（即一题多解），同时学生从条件、结论入手，延伸、改编问题，或提出新问题（即一题多变，多题归一）。在“解决问题”教学过程中，既有解决问题前的分析——弄清条件与结论，明确解决思路，又有解决问题后的反思——积淀转化问题的数学活动经验，感悟问题中蕴含的数学思想方法和核心素养。既有教师引导下学生的思考与交流，又有教师的经典性评析。这一过程极大地促进了学生数学能力的提高。

（三）促进发展，落实素养

《义务教育数学课程标准（2011年版）》把问题解决作为课程目标之一，并指出：要使学生获得分析问题和解决问题的一些基本方法，体验解决问题方法的多样性，发展创新意识。数学解题是数学学习中的核心活动，是数学思维的实质化，解题的核心价值就是运用数学知识。解题教学如果仅限于教会学生解课堂上的题目，不能举一反三，学生就会陷入茫茫题海，导致思维固化，渐渐失去学习数学的兴趣。根据波利亚“怎样解题”理论，只有引导学生深入了解问题中的已知条件，分析已知条件和待求结论的内在联系，把握解决问题的关键所在，才能把握每一类数学问题的本质。教学中，教师不能只关注题目的结果，更应该了解学生的思维方式和思路的形成过程。学生在解决问题的每一次思维过程中，不断体验基本数学活动经验，获得基本数学思想方法，发展综合能力。

波利亚“怎样解题”理论在数学教材中并没有明显地呈现出来，但在大多数情况下，它隐含于数学知识和问题解决的过程中，需要教师不断地进行提炼和概括。在课堂教学中，教师应当设计有效的数学活动，引导学生提炼问题情境，检索数学知识，激活解题思路，不断地反思解题过程。在解决问题的过程中，既培养学生良好的思维习惯，使其学会学习的技能，理解数学知识的本质，又给学生提供可应用于其他学科的推理方法，培养学生的数学核心素养，从而促进学生的全面发展。

参考文献：

[1]G.波利亚.怎样解题[M].上海：上海科技教育出版社，2007年.

[2]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.