直流偏磁下变压器绕组振动特性分析

吕舒艺，李晓华，章李烽，赵文彬，夏能弘，黄堃，杨勇

（1.上海电力大学电力工程学院，上海 200090；2.广州供电局有限公司，广东广州 510245）

变压器作为电网运行中重要的设备之一，其安全稳定的运行与整个电力系统的可靠性密切相关，随着超高压直流输电系统（high voltage direct current，HVDC）在我国的广泛使用，在变电站附近中性点接地的变压器中出现了直流偏磁现象[1-2]。直流偏磁会导致变压器振动异常、噪声加剧，长期处于偏磁影响下的变压器发生绕组变形、松动等故障的概率加大，影响变压器的稳定运行[3-4]。因此，有必要对直流偏磁下绕组振动特性进行研究和分析。

国内外对于直流偏磁下变压器的偏磁及振动特性研究已有一定基础。Hassan等人建立了单相变压器仿真模型，通过谐波特性分析研究了直流偏磁分量对变压器励磁特性的影响[5]。梁贵书等人提出了用两个质量单元表示绕组的一个线饼，单元之间由弹簧连接的二维模型。但是该模型将垫块等效为弹簧时仅能考虑其弹性特征，未能考虑垫块的材料特性，同时无法考虑绕组几何结构对振动的影响，导致其与绕组实际振动存在一定误差[6]。第二类模型是利用有限元进行建模分析。罗彤等人采用有限元模型研究了在额定负载条件下变压器的电磁特性和振动特性，并通过实验进行了验证[7]。徐永明等人计算了变压器在短路时的短路电动力和在电动力影响下绕组的应力特性，得出了绕组不同位置的应力分布[8]。但是现有的研究在研究绕组的电动力时，对于直流偏磁下发生短路故障时绕组的振动特性研究较少。变压器长期处于偏磁影响下时，即使偏磁电流不大，但长期以往其机械稳定性会受到影响，发生短路故障时造成绕组损坏的概率会变大。

文中借助仿真软件建立了变压器三维仿真模型，仿真分析了有/无偏磁条件下发生短路故障时绕组的短路电流和振动位移特性及其变化规律，并使用分布反馈光纤激光器（distributed feedback fiber laser，DFB-FL）搭建实验平台对模型进行了验证。

1 变压器绕组振动机理及DFB 激光器测量原理

1.1 绕组振动电磁力分析

当变压器带负载运行时，由于绕组中电流的影响，除了在变压器铁心中流动的主磁通外，还有漏磁通穿过绕组及结构件。绕组在交变漏磁通的影响下产生交变的电动力，绕组在交变的电动力的作用下会产生振动。振动的大小与漏磁通的大小和绕组中流过电流的大小有关。

绕组中电流在轴向产生轴向漏磁场Bzt，轴向漏磁场与绕组电流相互作用产生辐向力Fx；同样，绕组电流在辐向产生辐向漏磁场Bxt，辐向漏磁场与负载电流相互作用产生轴向力Fz，轴向力向内压缩低压和高压绕组，在辐向力的作用下，低压绕组向内压缩，高压绕组向外扩张。绕组在磁场中的受力如图1所示。

图1 绕组在磁场中的受力Fig.1 The force of the winding in the magnetic field

依据前面对绕组的受力分析可知，作用在绕组上的电磁力可表示为[9]

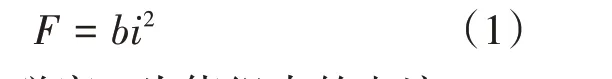
式中：b为流过绕组的磁密；i为绕组中的电流。

当有直流偏磁时，绕组中会有直流分量流过，同时激磁电流中还包含其他频率的谐波分量，此时i可表示为

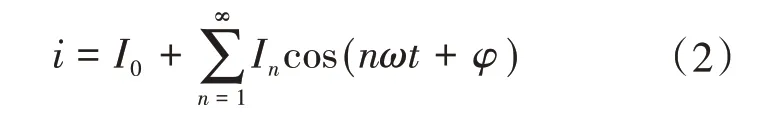
式中：I0为直流分量；n为偏磁电流中常见的谐波分量，一般为2 次、3 次、4 次、5 次谐波；ω为外部磁场的变化频率；φ为相位角。将式（2）代入式（1）可得：

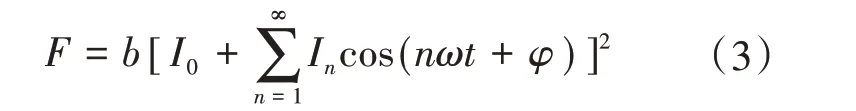
单独计算每次谐波电流产生的F并求和可以得出直流偏磁下变压器绕组所受到得电磁力表达式[10]如下式：

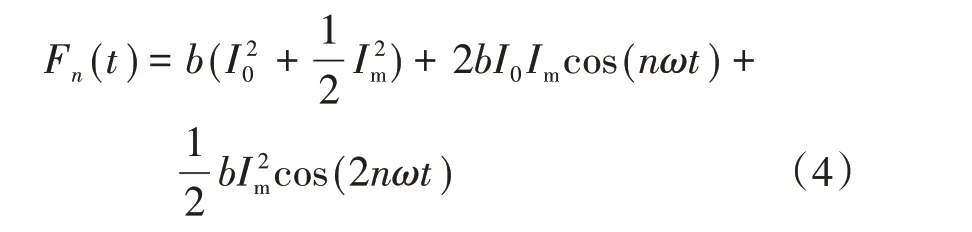
式中：Im为电流幅值。

通过对式（4）中等号右侧的第2 项、第3 项分析可知：当有直流偏磁时，由于受到电流中暂态分量的影响，绕组振动中同时包含偶倍频和奇倍频分量。

1.2 绕组振动位移分析

在绕组的振动位移分析中，将绕组按照由绝缘垫块层层分开的结构进行分析，此时绕组假设为质量为m的质量块，绝缘垫块假设为弹簧，用KB，K，KH表示，绕组间的阻尼系数为CB，C，CH，绕组的位移用z表示，绕组的受力表示为F。此时建立出绕组的振动位移方程如下式所示：

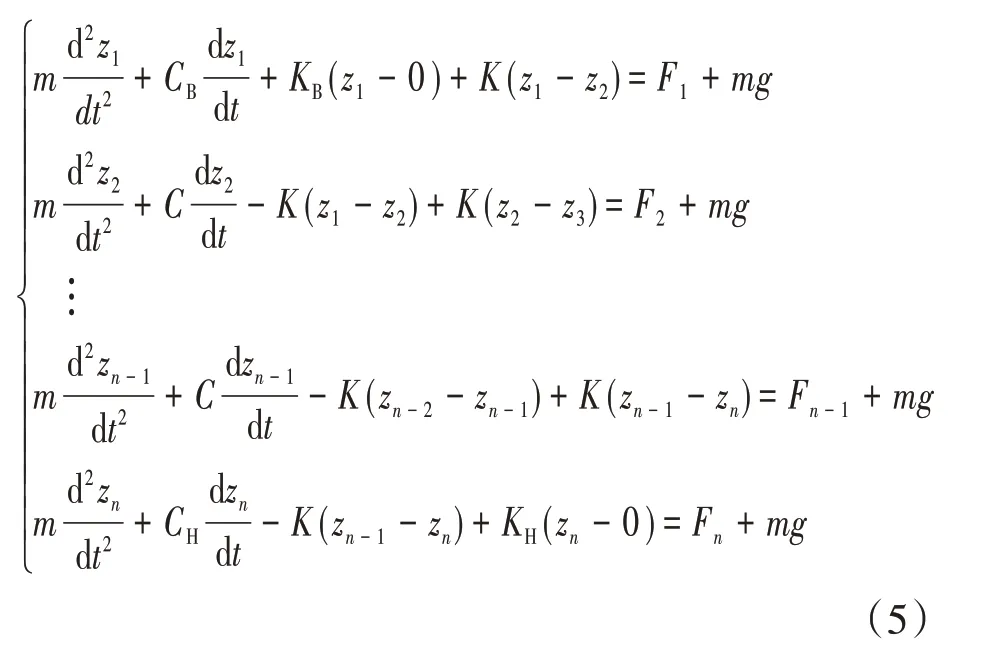
由方程可知其中未知数和方程数相同，即此时方程有唯一解，但每个绕组的阻尼系数和弹性系数都不相同，若直接使用会使计算不易收敛。为了简化计算，将绕组的振动看作为整体的振动，即z1=z2=…=zn=z，将方程左右两边相加可得：

式中：mˉ为数个绝缘垫块质量的平均数；N为绝缘垫块个数。

将式（6）和上文求出的绕组所受电磁力结合得到：

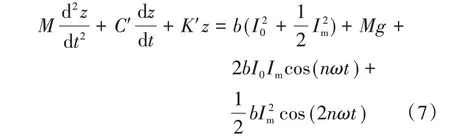
1.3 DFB激光器测量原理

传统的压电式传感器易受到电磁干扰，影响测量结果，并且体积大，不宜放置，因此，文中在进行试验验证时，采用分布式反馈光纤激光器（DFB-FL）作为测量设备。

DFB 光纤激光器上刻有光栅。光纤光栅周期长度为Λ时，只有满足布拉格反射条件波长为λB的光波，才能产生激光震荡，使激光器得到单频输出。由于分布式反馈激光器是由光栅选择单纵模，因而在高速调制下仍维持单纵模输出。Λ的计算式如下式：

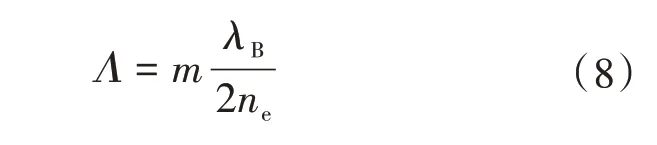
式中：Λ为光栅周期；ne为光纤有效折射率；λB为反射波长。

以往的DFB 激光器多用在水听器、温度的检测中[11-12]，作为振动检测使用较为少见。图2是DFB 激光器的测振原理，λn表示反射波长。980 nm 泵浦光源发出的泵浦光经980/1 550 nm波分复用器（wavelength division multiplexing，WDM）的980 nm 端口传输到由DFB 激光器组成的传感头上，利用WDM 能够将多种携带各种信息的光载波信号整合和分离的能力，可以将由DFB 激光器产生的激光经过980/1 550 nm WDM的1 550 nm 端输出，通过波长解调仪进行振动数据的分析。

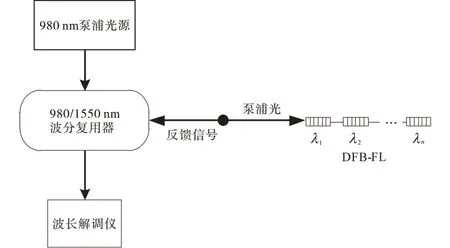
图2 DFB激光器测振原理图Fig.2 DFB laser measurement vibration schematic

DFB 激光器粘贴在悬臂梁上，当悬臂梁振动的时候，刻写在DFB 激光器上的光纤光栅的中心波长会移动，从而引起DFB 激光器中心波长的移动，振动越大，中心波长的移动越多，从而可以根据激光器中心波长移动的大小来判断振动的大小。

2 有限元模型及振动仿真分析

2.1 有限元模型

文中以一台匝数比77/1 785，电压等级220/5 000 V，额定容量20 kV·A 的单相实验变压器为对象进行有限元建模分析，主要研究在有/无直流偏磁的影响下变压器绕组的振动特性。由于真实的变压器结构比较复杂，对模型进行了适当的简化。忽略了夹件和螺杆等部件，将铁心和绕组的外部空间设为空气，并利用插值函数的方法定义B—H曲线来定义铁磁材料，为绕组添加线圈几何分析并将材料属性设定为铜，绕组首末两端设置固定约束来模拟实际情况。绝缘垫块的弹性模量随其受到的力的变化而变化，所以在材料设置中将绝缘垫块的材料属性定义为非线性弹性材料。为了提高整体仿真的精确度，对变压器不同的部位采用不同的网络结构，需要重点分析的绕组部位采用较细化的网格，其他部分采用常规网格。

为了提高运算效率，绕组共分6层，初级和次级绕组每层初始垫块数量为4个。整体模型如图3所示，共104 515个域单元。

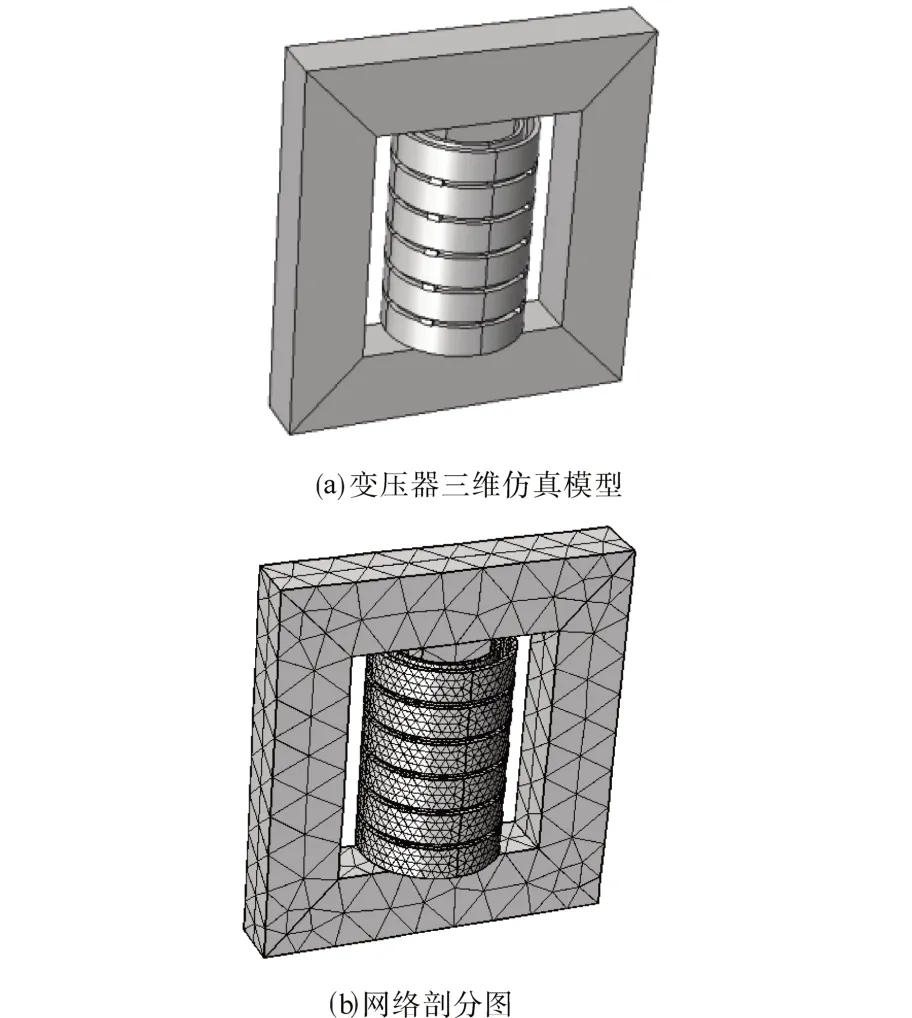
图3 变压器有限元模型Fig.3 Finite element model of transformer

在以往对变压器绕组振动的研究中，对于在直流偏磁的影响下发生短路故障时绕组振动的研究较为少见。文中通过有限元模型和外电路的耦合，建立由低压、高压绕组和交流、直流源组成的等效电路，其中直流偏磁通过直流源引入，外电路由交、直流源叠加组成，同时设置单相变压器仿真模型在40 ms 时发生短路故障，研究有/无偏磁情况下发生短路故障时，绕组振动特性的变化。偏磁仿真电路图和绕组振动有限元分析流程图如图4、图5所示。

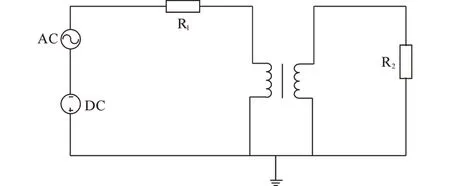
图4 偏磁仿真电路图Fig.4 Bias magnetic simulation circuit diagram

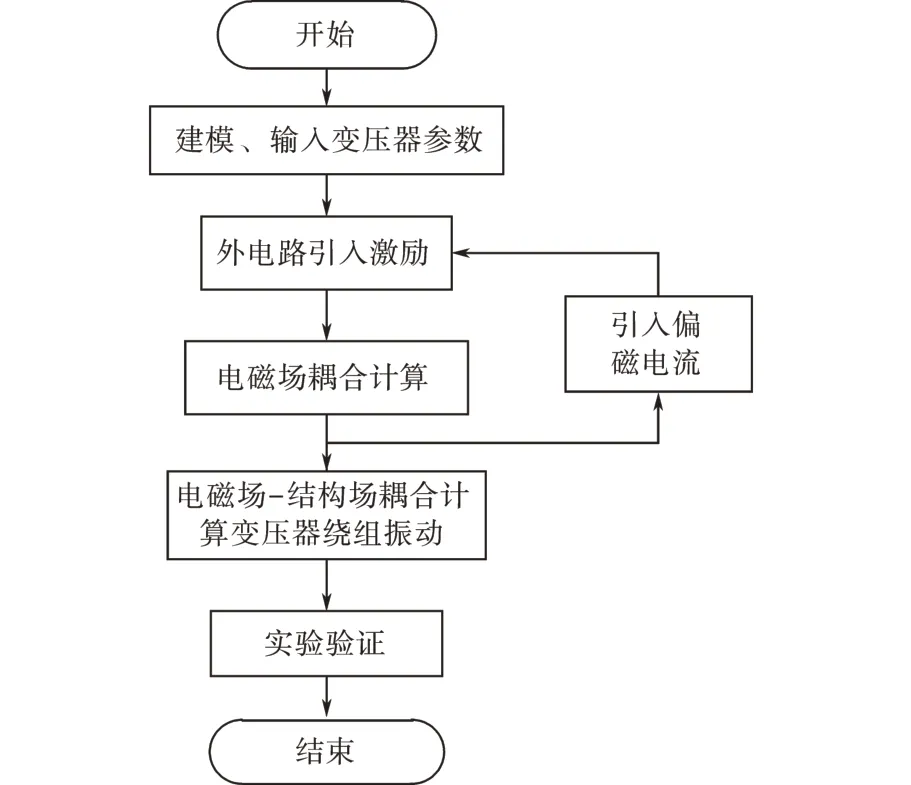
图5 绕组振动有限元分析流程图Fig.5 Windings vibration finite element analysis flow chart

电场模块方程为

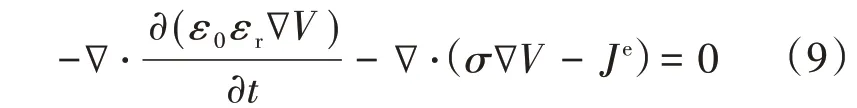
式中：ε0为自由空间的介电常数；εr为相对介电常数；σ为电导率；Je为外部电流密度；V为电势。

将图4外电路中计算出来的电流作为激励引入到变压器模型中的线圈中，实现电场和磁场的耦合，磁场模块的方程为

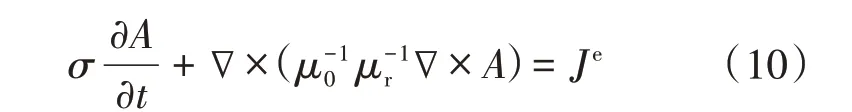
式中：μ0为自由空间的磁导率：μr为相对磁导率：A为矢量磁位。

将电磁场模块中求得的b，Je等参数作为初值代入到式（10）中，实现电磁场和结构场的二次耦合，计算得到绕组的加速度和应力应变，结构场的求解域方程为

式中：md2u/dt2为绕组惯性力；ζdu/dt为绕组阻尼力；ku为绕组绝缘弹性力；Ft为绕组受到的随时变化的电磁力。

绝缘垫块的应力-应变关系可表示为[17]

式中：σ，ε为绝缘垫块的应力、应变；ao，bo为线性系数和硬化系数。

由式（12）可推出垫块弹性模量的计算公式为

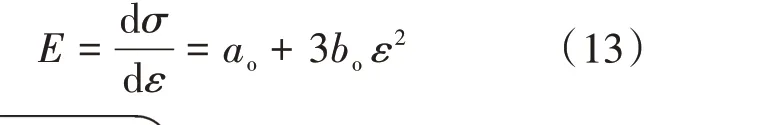
2.2 仿真结果及分析

变压器在突发短路故障时，短路电流的峰值可达额定电流的数十倍之多。为了研究突发短路故障时绕组的振动特性，文章在软件中设置单相变压器仿真模型在40 ms 时发生短路故障，分析在有/无偏磁情况下发生短路故障时绕组的振动特性。在实际情况中绕组上、下部都有紧固件进行约束，文中在仿真软件中忽略了上、下部的紧固件，通过在绕组上、下底面施加固定约束来模拟紧固件的作用，使仿真和实际更加贴近。

图6 是有/无偏磁情况下绕组发生短路故障时二次侧的电流波形。从图6 中可以看出，在无偏磁时短路电流的峰值约为正常额定电流的17倍，在偏磁情况下短路电流在达到第1个峰值时会发生偏移，随着偏磁电流的增大，偏移也随之增大，经过约6个周期后波形衰减为稳态短路电流。

图6 短路时二次侧电流波形Fig.6 Secondary side current waveforms during short circuit

由于不同偏磁电流下短路电流峰值的偏移较整体来说不易从图中看出变化趋势，将不同偏磁情况下短路电流的峰值单独取出作图，如图7所示。从图7中可知，随着偏磁电流的增加，短路电流峰值呈现出逐步稳定增加的趋势，当偏磁电流接近4 A 时，增加逐渐平缓，这是因为文中研究的实验变压器容量较小，所能承受的偏磁电流幅值较低，在偏磁电流达到4 A 左右时，就已接近所允许通入的偏磁电流幅值。当偏磁达到2 A 时，短路电流峰值较无偏磁情况下增加了约5.43%。

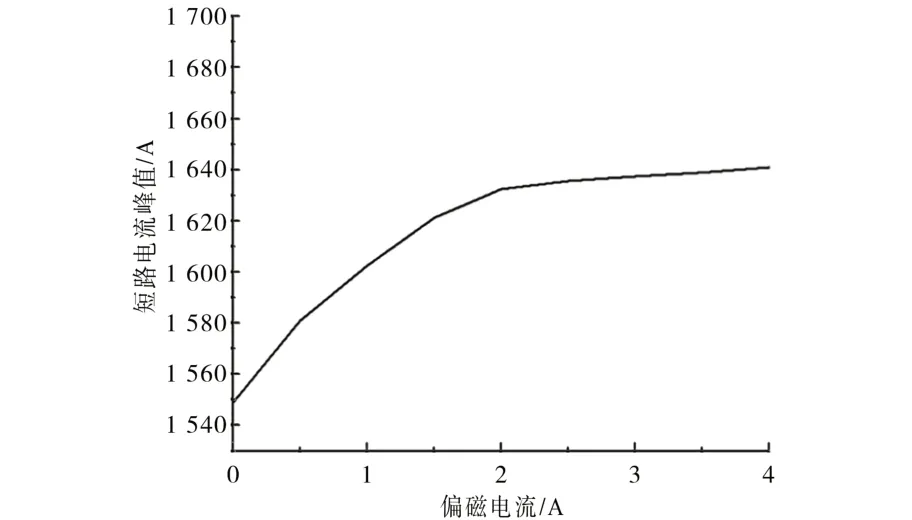
图7 不同偏磁电流下短路电流峰值Fig.7 Short-circuit current peak under different bias currents

图8是不同偏磁电流下短路电流各次谐波的含量及变化趋势，电流基频为50 Hz。由图8 可知，短路电流谐波频谱中2 次、3 次、4 次谐波含量较多，同时含有少量其他倍频谐波分量。

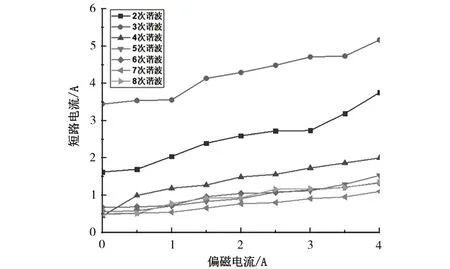
图8 不同偏磁电流下短路电流各次谐波Fig.8 Short-circuit current harmonics under different bias currents

由于在绕组端部漏磁较大，绕组会受到较大的短路电动力，所以以第1饼为例，分析此处在有/无偏磁情况下发生短路故障时所受到的应力，结果如图9 所示。由图9 可知，在发生短路故障时，绕组受到巨大的短路电动力，其中包含暂态分量和稳态分量，随着暂态分量的逐渐衰减，短路电动力逐渐趋于稳定。在不同的偏磁电流下，绕组受到的短路电动力最大值变化如图10 所示。由图10可知，随着偏磁电流的增加，绕组受到的最大短路电动力逐步增加，当偏磁2 A 时，较无偏磁情况下的最大短路电动力增加了约6.68%。

图9 短路冲击下低压绕组1饼处的应力分布Fig.9 Stress distribution of first low voltage winding under short-circuit impulse

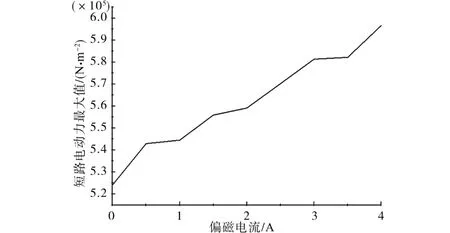
图10 不同偏磁电流下短路电动力最大值Fig.10 Short-circuit electric power maximum under different bias currents

图11 是不同偏磁电流下绕组短路电动力的谐波分布。由图11 可知，在不同的偏磁电流下，短路电动力各次谐波中150 Hz，200 Hz，250 Hz 等谐波分量含量较多，同时增长趋势较其他谐波分量也更明显。

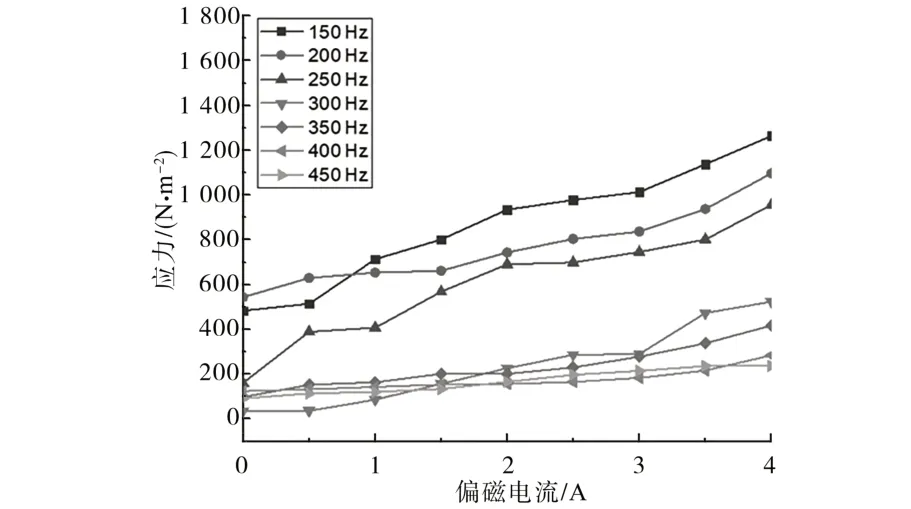
图11 不同偏磁电流下短路电动力各次谐波Fig.11 Short-circuit electric dynamic harmonic under different bias currents

图12 是有/无偏磁情况下发生短路故障时低压绕组1 饼处的振动位移波形。由图12 可知，当发生短路故障时绕组振动出现更加复杂的变化特性，位移特性和电流及应力一样，也存在暂态分量和稳态分量，在短路后约10 ms 时达到最大值，随着暂态分量的衰减逐渐趋于稳定。

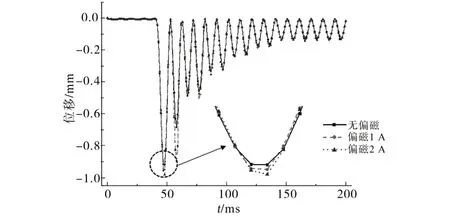
图12 短路冲击下低压绕组1饼处的位移波形Fig.12 Displacement waveforms of the low-voltage winding 1 under the short-circuit impact

在不同偏磁电流下突发短路故障时，位移最大值的变化趋势不易从波形图中直接看出，故将不同偏磁电流下突发短路故障时绕组位移的最大值取出分析，如图13 所示。由图13 可知，绕组最大位移在偏磁电流的影响下呈现出和应力相似的变化趋势。当偏磁2 A 时，绕组位移最大值增加了约6.75%。

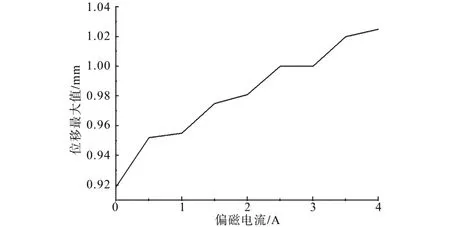
图13 不同偏磁电流下绕组位移最大值Fig.13 Maximum winding displacement under different bias currents

图14 是不同偏磁电流下低压绕组1 饼处的振动位移频谱分布。由图14可知，其谐波分量分布和应力的谐波分量相似，包含150 Hz，200 Hz，250 Hz 等谐波分量，并且随着偏磁电流的增加，有着较为明显的增长趋势。

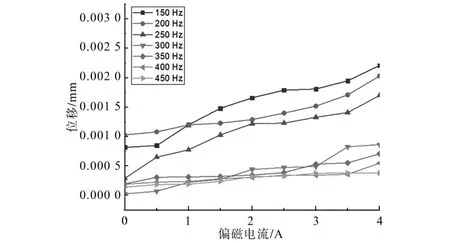
图14 不同偏磁电流下低压绕组1饼处的振动频谱Fig.14 Vibration spectrum of cake at low voltage winding 1 under different bias currents

通过对直流偏磁下变压器绕组振动的仿真结果分析可知，短路电流、短路电动力、振动位移都包含暂态分量和稳态分量，当偏磁电流达到2 A 时，最大短路电流增加了5.43%，最大短路电动力增加了6.68%，随着偏磁电流的增加，短路电流频谱中除了占据主要分量的基波外，还包含部分的100 Hz，150 Hz 及少量其他倍频谐波分量，短路电动力除了基频分量外还包含部分150 Hz，200 Hz，250 Hz 等谐波分量。虽然直流偏磁造成的短路电流和振动位移偏移量较整体而言没有很大，但是变压器在实际运行中长期受到偏磁的影响时，因其包含各种谐波分量，会造成变压器振动更加复杂，长期以往会对机械稳定性和使用寿命造成影响。

3 试验研究

为了验证的方便，选择无偏磁情况下绕组的加速度仿真结果和实验结果进行对比。以一台容量20 kV·A、电压等级5 000/220 V 的实验变压器为研究对象建立了变压器振动测试平台。由于传统的压电式传感器容易受到电磁场等外部干扰的影响，本次试验采用DFB 激光器进行测试。实验平台由高灵敏度DFB 光纤振动传感器、传输光纤、解调仪、笔记本组成。实验装置如图15所示。

图15 振动测试装置现场图Fig.15 Vibration test device site map

以仿真模型中绕组1/5 处的振动为例，仿真此位置振动加速度及频谱分析，如图16所示。在试验时将绕组低压侧短路，测得的加速度及频谱分析如图17所示。

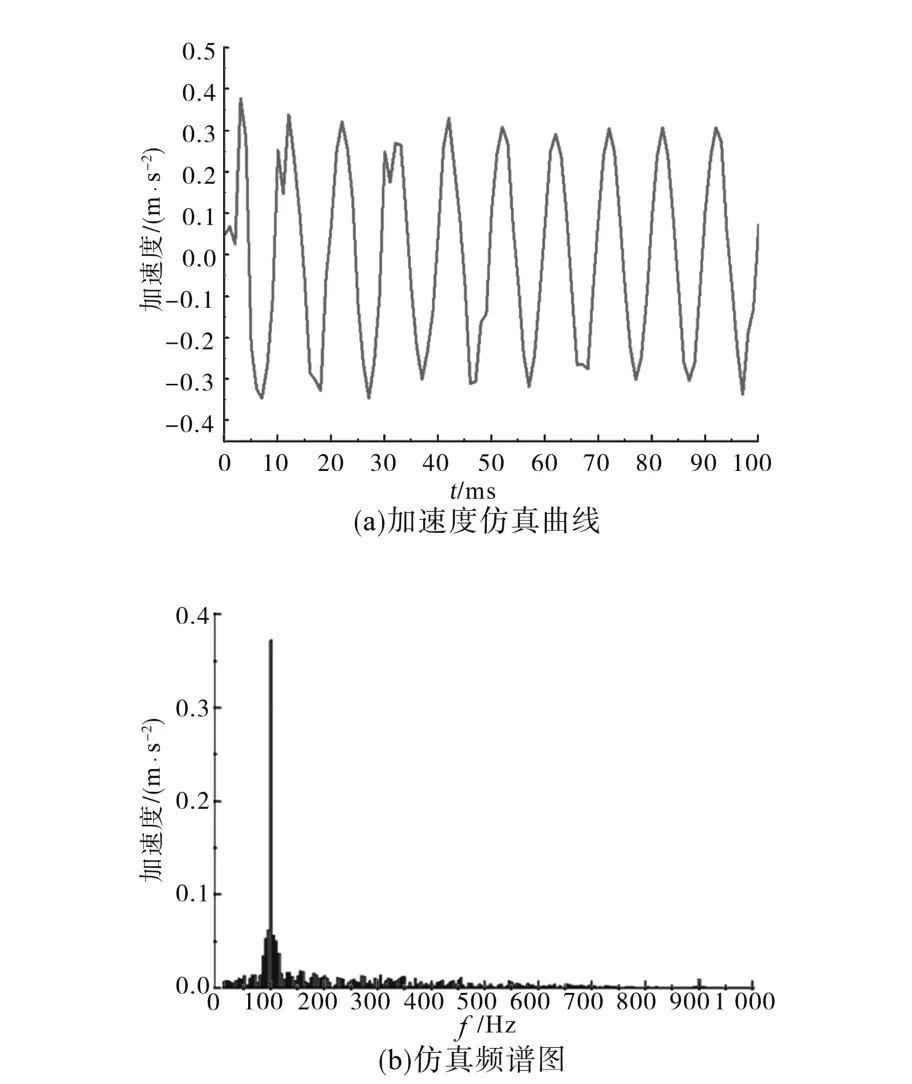
图16 绕组加速度仿真值Fig.16 Winding acceleration simulation value

图17 绕组加速度实测值Fig.17 Winding acceleration measured value

对比加速度的仿真和实测值可知，频谱结果都是以100 Hz 为基准值，并且占主要分量，这与已有结论一致。仿真频谱中含有少量的低次谐波信号，主要都分布在500 Hz 以下，这是由于仿真模型中考虑了材料的非线性，使得加速度曲线中含有毛刺所致。仿真和实验加速度曲线的幅值和振动波形基本一致，总体上仿真结果和实验结果吻合较好，证明了所建的变压器绕组仿真模型的准确性。

4 结论

文中借助于有限元软件对不同偏磁情况下变压器发生短路故障时的绕组振动进行了仿真分析，结果表明：

1）所搭建的变压器三维仿真模型基于多物理场的耦合，能够有效实现不同偏磁电流下发生短路故障时变压器绕组振动的仿真。

2）在不同偏磁电流下发生短路故障时，短路电流及短路电动力瞬间增大，且随着暂态分量的衰减逐渐平稳。绕组振动特征呈现出更加复杂的变化，其频谱分量中包含150 Hz，200 Hz，250 Hz等低次谐波分量。

3）通过试验和仿真结果的对比，验证了仿真模型及分析方法的正确性，文中的模型对分析直流偏磁下变压器绕组的振动和变压器的在线监测有一定的借鉴意义。