轨道方程平滑方法在轨道预报中的应用

朱时银，刘利军，李 曦

(中国人民解放军63620部队，甘肃 酒泉 732750)

航天器的轨道预报和落点预报是航天活动的一项主要任务。轨道预报是指根据测量设备的观测数据，按航天器轨道模型和摄动因素计算轨道根数，然后再推算航天器未来时刻的运行轨道。落点预报计算过程中还需要考虑气动模型。轨道预报的关键是由观测数据计算轨道根数，观测数据通常只有航天器的定位测元信息，并且受测量数据随机误差影响，限制了轨道预报精度。本文就如何提高航天器轨道根数计算精度开展讨论，即如何消弱测量数据的随机误差以提高预报的速度参数精度。

轨道观测设备通常不具备测速能力，速度参数需要由其他方式来获取，例如多项式平滑微分和卡尔曼滤波等[1-4]。文献[1]和文献[3]基于航天器轨道局部可用多项式来表示这一假设，使用多项式拟合平滑来消弱随机误差，通过微分运算计算速度参数。由于此类方法只使用部分测量数据，且存在模型误差，获取的航天器速度参数精度有限，只适用于短时段轨道预报。文献[2]给出了基于卡尔曼滤波的观测数据处理方法，其状态方程本质还是多项式，效果与多项式平滑类似。文献[4]给出了基于动力学方程的弹道预报方法。但该文重点是利用轨道根数计算未来时刻运行轨道，没有给出初始轨道根数计算方法。

本文依据航天器自由段轨道符合椭圆轨道方程这一事实，提出使用轨道方程来拟合自由段轨道，以获取高精度的速度参数。由于这种表示方法对整个自由段轨道都是有效的，可以使用全部测量数据来进行估计，极大消弱了随机误差的影响，显著提高了航天器轨道参数，特别是速度参数的解算精度，为进行航天器轨道预报和落点预报提供了高精度的初始轨道，从而可以显著提高预报数据的稳定性和预报精度。

1 轨道方程平滑方法

1.1 开普勒轨道根数及计算

由开普勒定理可知，自由段轨道可以看成椭圆轨道的一部分，可以由6个基本参数完全确定，这些基本参数称为轨道根数，分别是：长半轴a、轨道偏心率e、轨道倾角i、升交点赤经Ω、近地点幅角ω和过近地点时刻tp[5-6]。在这6个开普勒轨道根数中，长半轴a和偏心率e决定了椭圆轨道的大小和形状；倾角i和升交点赤经Ω决定了轨道平面在空间的位置；近地点幅角ω决定了椭圆在轨道平面上的方位；由于长半轴a已决定了轨道运行一周的周期，又由开普勒第二定律可知，只要已知近地点时刻tp，就可以确定任意时刻(历元)在轨道上的近地点到该点的平近点角M(M为假定航天器以平均角速度在轨道上运行，从过近地点时刻到该时刻运行的角度)。

如果已知某历元时刻t0的平近点角M0(0≤M0≤360°)，则轨道在其过近地点时刻t0的假想平均角速度为2π/T，记为n，而经过的角距等于n(t0-tp)，这样任意时刻t的平近点角M=M0+n(t-t0)=n(t-tp)。因此，有时开普勒根数可用某历元时刻t0的平近点角M0代替过近地点时刻tp，作为轨道根数之一。

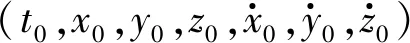
1.2 基于轨道方程的拟合平滑

轨道方程平滑就是使用已获取的所有自由段轨道数据来确定轨道根数，即使用轨道方程来拟合轨道，也可以看作为精确轨道的确定，具体计算方法如下。

(1)

(2)

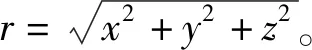
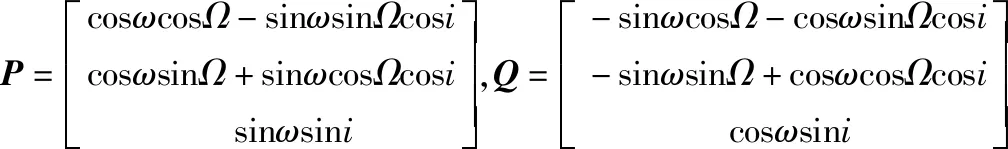
(3)

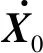
(4)

式中，

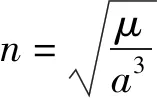
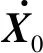
2 轨道方程拟合平滑方法的应用

2.1 轨道预报方法

使用的轨道预报方法基于地心坐标系，考虑了重力、牵连惯性力、柯氏惯性力和空气阻力等外力[10-11]，相对地心直角坐标系的被动段目标运动方程为

(5)

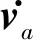
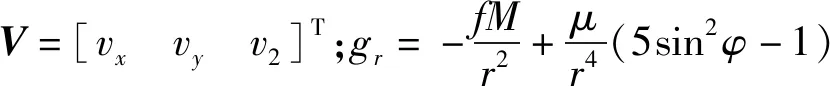
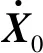
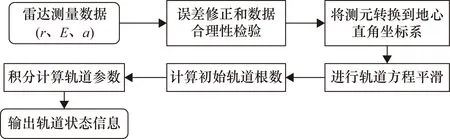
图1 基于轨道方程平滑的轨道与落点预报处理流程

将某航天器GNSS测量数据预报轨道与实测轨道作差(预报起始时间为300 s和400 s)，结果如图2所示。从比对结果来看，向后预报350 s和250 s的轨道误差分别小于100 m和70 m。这说明本文采用的经典轨道预报算法可以满足轨道预报处理的高精度要求，关键是起始历元t0状态的精度，特别是速度参数的精度。

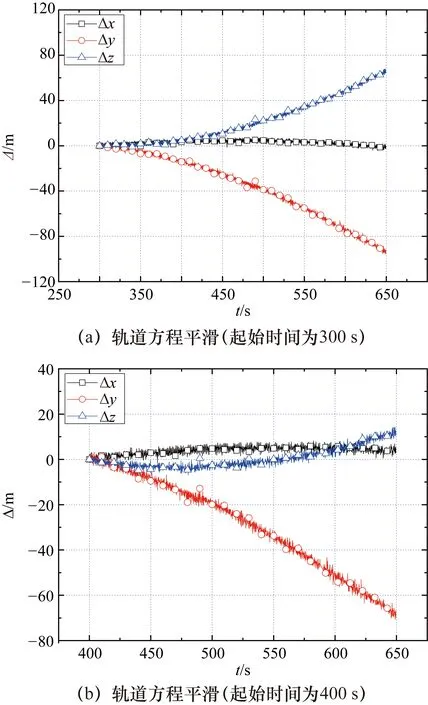
图2 某航天器GNSS预报轨道和实测轨道作差结果

下面从轨道预报和落点预报两个应用情况来比较多项式平滑和轨道方程平滑的精度。

2.2 轨道预报应用情况

使用前面某航天器雷达测量数据进行计算分析。某雷达从相对时295 s开始获取目标轨道数据。使用400 s前测量数据计算轨道根数，然后从400 s开始进行轨道预报，将雷达预报轨道与GNSS实测轨道进行比对，以评估预报初始状态估计方法的精度。使用多项式平滑和轨道平滑的比对结果如图3所示。

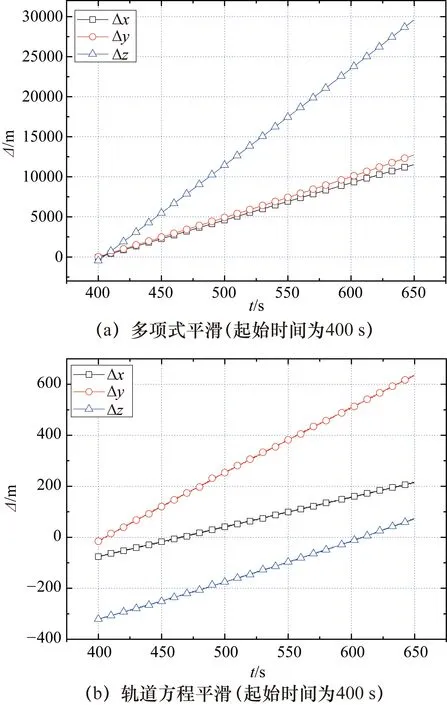
图3 某雷达预报轨道和GNSS实测轨道作差结果

由图3可见，采用轨道方程方法对航天器测量数据进行平滑，航天器轨道预报结果从30000 m减小至600 m，预报精度提高了1～2个数量级，效果明显。

同样在此测试项目中，某雷达获取了航天器及其伴飞物的504～547 s轨道数据，从295 s开始获取主目标轨道数据。项目分析过程中，需要确定伴飞物从主目标分离的时间，这样就需要计算伴飞物的飞行轨道。将伴飞物测量数据平滑处理后计算初始轨道，并向前预报，然后与主目标轨道进行比对，以估计分离时间。多项式平滑和轨道方程平滑预报轨道计算的伴飞物与主目标的相对距离如图4所示。

从图4可知，使用轨道方程平滑计算的距离更可信，伴飞物与主目标的相对距离最小约为200 m，更接近实际情况(得到目标实际分离时间约为125 s)。采用雷达测量数据进行航天器轨道和落点预报，与使用GNSS测量数据的预报结果相比，其预报精度还有差距。这与雷达测量设备的系统误差有关，平滑只能消弱随机误差的影响。因此，轨道测量设备系统误差实时估计也是提高预报精度的关键技术。

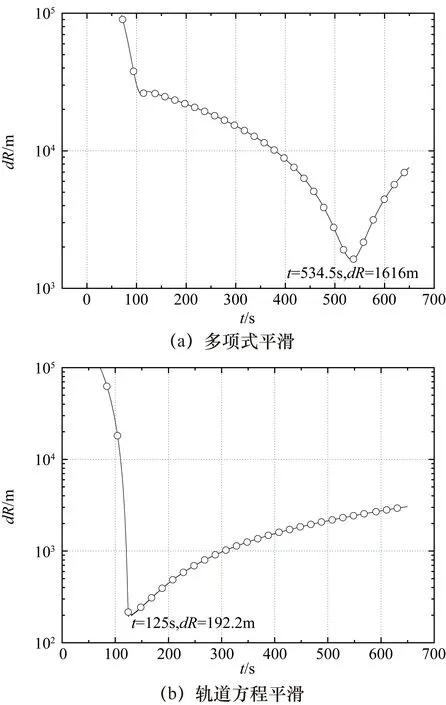
图4 雷达轨道预报的目标相对距离

2.3 落点预报应用情况

针对不机动飞行目标，可以使用前面计算的轨道预报方法(加空气阻力模型)预报其落点。如果获取了目标再入大气的轨道，则可以估计空气阻力参数(即质阻比)；否则，可以使用经验值，圆锥状航天器的空气阻力系数取0.0001～0.0002、火箭箭体的空气阻力系数取0.01～0.05[14-15]。

在某落点预报仿真测试项目中，航天器返回大气层前为无动力飞行(即飞行过程中未发生机动)，使用雷达获取的轨道测量数据计算其落点散布(即使用不同时间段数据分别进行落点预报)，采用散布密度衡量落点预报方法的精度，即落点散布范围小的认为预报精度较高。某测试项目多项式平滑和轨道方程平滑计算的落点散布如图5所示。

图5 雷达轨道测量数据预报落点散布(经纬度偏差)

从落点经纬度偏差来看，轨道方程平滑落点预报相对多项式平滑方法散布范围更小，预报精度明显要高于多项式平滑。

3 结束语

为了提高轨道预报初始点的坐标和速度参数精度，根据航天器自由段轨道可以准确地使用轨道方程来逼近的理论，提出了基于轨道方程拟合的轨道平滑方法。从轨道预报和落点预报的应用效果来看，该方法较多项式平滑方法具有更高的精度，在航天测量数据处理中有较高的应用价值。但通过测试项目预报轨道和落点数据的处理结果分析可知，该方法只能消弱随机误差，因此对测量设备系统误差的估计还需进行后续研究。