盘车数据在水导摆度偏大处理中的应用
何旭辉,袁世铎,杨 环
(五凌电力有限公司五强溪水电厂,湖南 沅陵 419642)
0 引言
按设计间隙均调的导轴承瓦间隙,常常因为机组检修,轴线发生变化,而与机组实际运行不相匹配,其安全隐患在于间隙过大或过小引起的瓦温高、摆度大等问题,为保障机组持续安全稳定运行,需要一种更加科学的瓦间隙调整方法,将机组实际轴线,纳入到计算之中,从而将瓦间隙调整与机组实际运行工况相结合,优化机组运行摆度。
1 实例概述
某电厂水导瓦设计间隙为单边0.285 mm,按GB/T 8564-2003《水轮发电机组安装技术规范》要求,机组稳定工况下水导摆度值应不大于0.285×2×75%=0.428 mm,该电厂在此基础上,另设置此上限的80%为实际预警值,即在机组稳定运行过程中,水导摆度应满足小于0.342 mm的要求。
2019年,某电厂某号机组在检修过程中进行了轴线调整,轴线调整后,机组满负荷下水导X向摆度始终高于Y向摆度近0.15 mm,工况较差时,X向摆度平均值越上限可达0.395 mm,不满足电厂安全稳定运行要求。
针对该问题,电厂立即进行分析,最终根据瓦温、轴线轨迹图,确定根本问题由轴线与瓦间隙不匹配所致。
为确保新调整间隙符合机组安全稳定运行要求,需将机组轴线考虑到间隙调整计算中,为此,电厂根据盘车数据,结合瓦间隙调整工艺,得出一组更适用于新轴线的瓦间隙调整方案。
首先,需确定关键部位尺寸数据,该电厂的基本参数如表1所示。

表1 某电厂某号机组基本参数
2 调整方案计算
在水导瓦间隙调整过程中,首先应当确定机组中心符合要求,即空气间隙、迷宫环间隙符合要求,在机组中心满足要求后,再去进行水导瓦间隙调整。
为避免大轴移位,调整水导瓦前,应抱紧上导瓦,某电厂水导瓦型式为楔形块型,该型式通过楔形块与瓦背面接触,由楔形块下降推动瓦朝轴移动,其下降行程与瓦间隙动作比例为50∶1,即楔形块下降50 mm,水导瓦间隙减少1 mm。
2.1 水导瓦间隙测量过程
(1)在大轴+X,+Y方向分别打上一块监视百分表(调零),其区域的划分方法应与机组盘车时的划分方法一致;
(2)用深度游标卡尺测量瓦抱紧大轴前楔形块行程;
(3)将X、Y方向水导瓦抱紧大轴,其方法为用铜锤敲击楔形块至百分表动作至0.01 mm,再在对侧同样敲击楔形块至百分表动作至-0.01 mm,再回到首次敲击侧敲击楔形块至百分表动作至0,此时认为X、Y方向的水导瓦已抱紧大轴;
(4)将所有水导瓦抱紧大轴,其方法为用铜锤敲击楔形块至百分表动作至0.01 mm,再在对侧同样敲击楔形块至百分表动作至0;
(5)用深度游标卡尺测量瓦抱紧大轴后的楔形块行程;
(6)用抱紧后行程-抱紧前行程再通过比例换算,即为水导瓦间隙。
2.2 水导瓦间隙调整原则
(1)各方位总间隙应在设计值0.57±0.04 mm;
(2)水导瓦间隙分布应呈正弦曲线规律[1],不应忽大忽小,防止出现梅花状轴心轨迹引起大轴跳动;
(3)调整间隙双幅值不可超过设定值0.285×2=0.57±0.04 mm;
(4)计算应排除轴径向位移,即采用盘车数据中的净全摆度数据计算;
(5)间隙计算应以最大净全摆度数据确定,即间隙满足最大净全摆度要求。
现测的机组中心数据如表2和表3所示。

表2 空气间隙与上迷宫环间隙 mm

表3 下迷宫环间隙 mm
由此可知,机组中心合格,如机组中心不合格,应先推轴后,再进行瓦间隙调整。
本次间隙调整,选取盘车数据中的Y表数据进行计算,具体数据如表4所示。

表4 检修后盘车数据Y表 0.01 mm
应注意,表格中净全摆度数据,是在假定轴完全竖直情况下得出的计算数据,该方法只适用于刚性油箱下刚性盘车数据计算,而对于弹性油箱盘车数据,应再考虑镜板倾斜值,根据电厂设备实际尺寸及净全摆度数据,将推力净全摆度做轴对称,因摆度相对于轴长可忽略不计,因此近似可画出轴线图如图1所示。
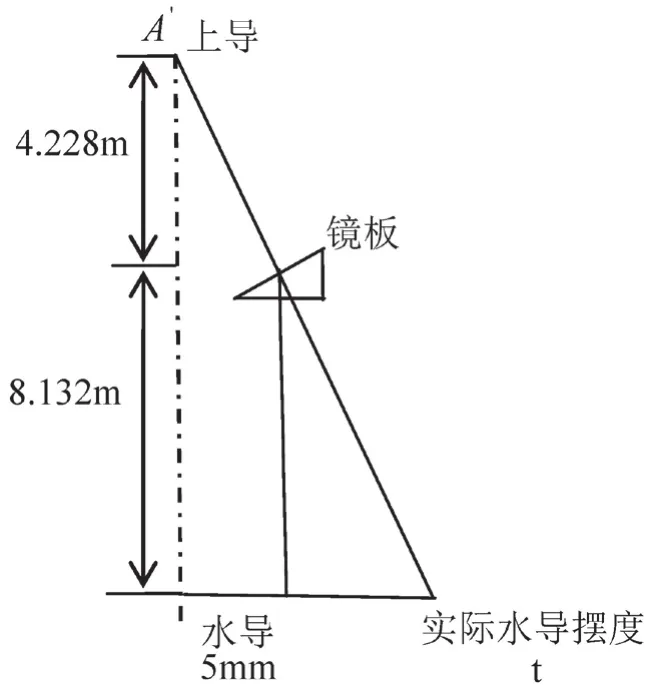
图1 轴线图
由相似三角形原理[2-5],镜板直径4.1 m可知:

因此,净全摆度修正见表5。

表5 修正后水导摆度数据表 0.01 mm
盘车净全摆度数据因测点数量限制,记录数据可能并非水导净全摆度最大处,因此需对数据进行处理,处理过程中将已有净全摆度数据进行向量合成,取其最大值,详情如下:

由计算可知,e(1-5,3-7)>e(2-6,4-8),因此取e(1-5,3-7)作为最大净摆度值,设为e,画出图形如图2所示。
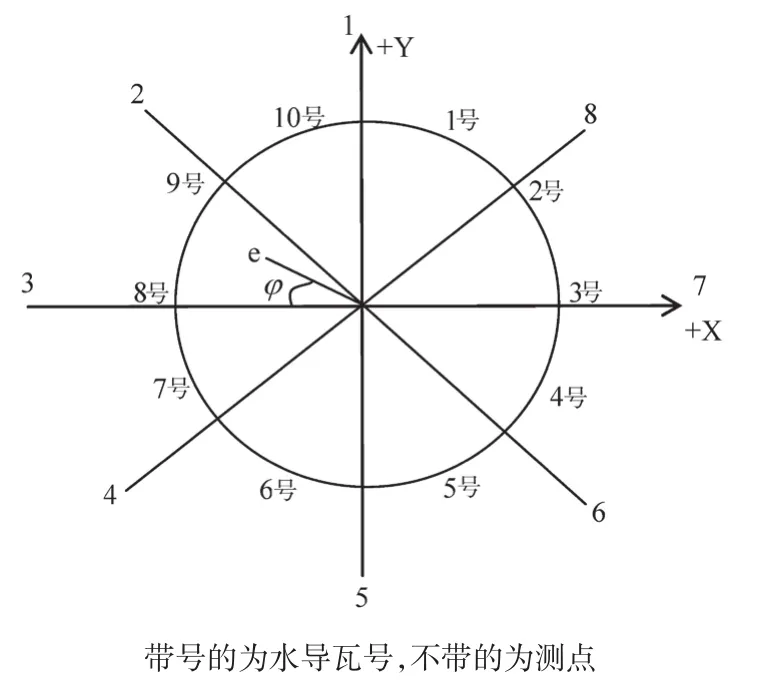
图2 轴瓦位置及测点位置图
现量得4号机水导瓦间隙如表6。

表6 水导瓦间隙实际测量图
将数据导入EXCEL表格,利用雷达图功能,可得出测量数据的方位分布图,如图3所示。
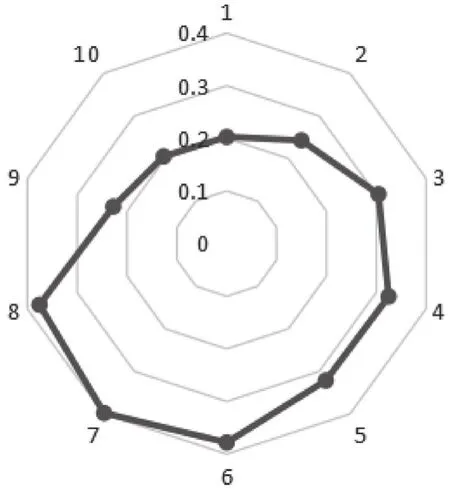
图3 水导瓦测量间隙分布图
由图3可知,测量间隙数据呈椭圆形状,不符合水导瓦间隙正弦(圆形)分布规律,可能由测量误差、读数误差、抱轴不紧等多因素导致,需对测量数据值进行正弦拟合修正,将误差降为最小,修正过程中,采用matlab进行编程,对测量数据进行y=esin(x+t)+k正弦拟合得出图4。
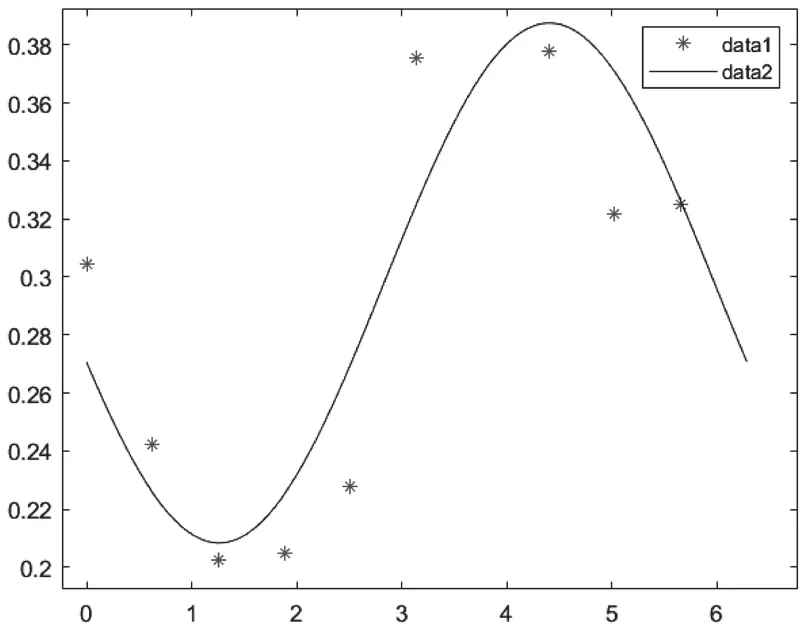
图4 测量间隙正弦拟合曲线
图中红点为实际数据点,曲线为拟合曲线,找出相同横坐标对应的拟合纵坐标,汇总得表7。

表7 水导瓦间隙正弦修正值 mm
通过验证,该数据修正与通过公式修正得出的结果相同,因拟合数据总间隙略大于设计间隙,对其数据再减0.01 mm,得到表8。

表8 水导瓦间隙设计修正值 mm
其雷达分布图如图5所示。
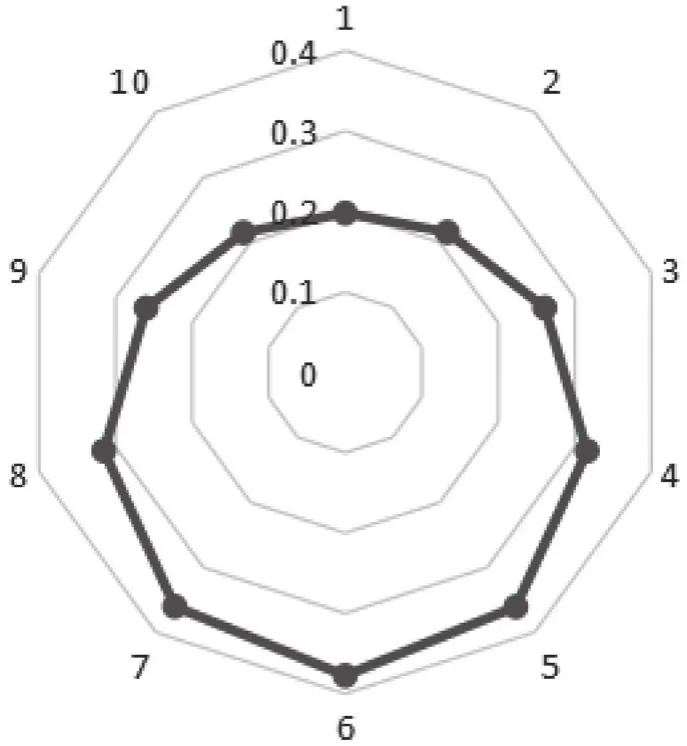
图5 水导瓦间隙修正分布图
由图可知,此时修正后的水导瓦间隙满足正弦分 布(圆形)规律,由 偏 转 量e=0.113 5,角 度φ=15.43°,各轴瓦间隙应调值=测量间隙,其中θ为最大净全摆度线与轴瓦的角度,由现场实际作业可调整的精度得出调瓦方案如表9所示。

表9 水导瓦间隙调整方案表 mm
调整后,对应瓦间隙分布图如图6所示。
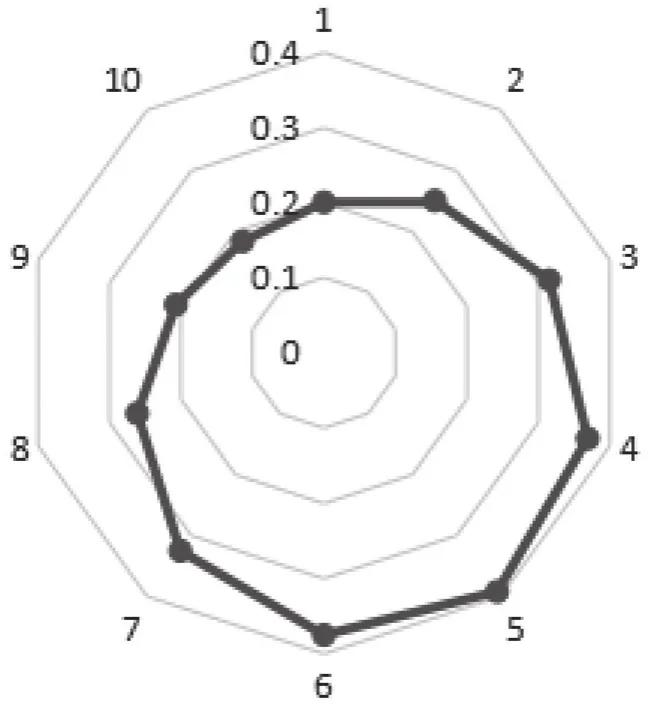
图6 应调瓦间隙分布图
由现场实际运行情况可知,5号瓦方向瓦温较高,8号瓦方向摆度较大,根据调整方案,瓦温高的5号瓦方向减垫间隙调大,温度降低,摆度大的8号瓦方向加垫间隙调小,摆度减少,符合现场实际情况。
在瓦间隙调整后,水导X向与Y向运行摆度近似相同,且最高摆度由近400 um恢复至300 um,瓦温最高由46 ℃恢复至42 ℃,符合生产运行各项标准条件,满足机组长周期安全稳定运行要求。
3 结语
本案例中使用的数据处理方法,较好的处理了因轴线与瓦间隙不匹配造成的X、Y向摆度差别大、摆度超标、瓦温过高等问题,实际调整过程中,可选取摆度较小的导轴承位置作为基准点,查询以往轴线调整后的盘车数据,进而进行瓦间隙适应性调整。
本次案例分析,为瓦间隙调整提供了理论依据,为我国水轮发电机组安全稳定运行,做出了贡献。

