GNSS辅助UWB基站位置估计方法

欧阳文，王安成，蒋理兴，罗豪龙

（信息工程大学 地理空间信息学院，郑州 450000）

0 引言

随着位置服务应用场景的不断拓展，室内外无缝定位问题被广泛关注。在开阔的室外，通常可以利用全球卫星导航系统（global navigation satellite system,GNSS）获得较高精度的位置信息。室内定位技术中，超宽带（ultra wide band,UWB）技术具有低功耗、抗干扰性强、穿透性强、定位精度高等特性，广泛应用于工厂、商场、养老院、煤矿和城市地下空间等场景[1-3]。因此，利用GNSS/UWB 组合实现室内外无缝定位成为研究热点。

在GNSS/UWB 室内外无缝定位系统中，GNSS一般使用大地坐标系作为基准，而UWB 室内定位基准取决于UWB基站的位置基准，与基站布设时位置确定方式有关，二者通常并不一致。在UWB基站布设问题上，已有文献大多借助全站仪[4]、测距仪[5]、运动捕捉系统[6]等高精度设备，也有学者提出了一些自标定方法。例如：文献[7]利用基站之间的距离约束信息采用卡尔曼滤波进行解算，这种方法定义的坐标系为局部的自由坐标系，基站不能得到室内外无缝定位场景所需的区域坐标；文献[8]提出了一种鲁棒的矩形形状UWB基站自标定方法，该方法过于依赖于基站之间的形状约束；文献[9]提出利用误差状态卡尔曼滤波（error state Kalman filtering,ESKF）对超宽带和惯性测量信息进行紧耦合，得到UWB基站位置，其本质是利用移动站的惯性测量单元（inertial measurement unit,IMU）位置姿态解算信息和UWB 测距信息对基站和移动站自身位置进行估计，该方法说明利用移动站坐标融合距离信息对基站进行位置估计是可行的。

受到文献[9]中利用移动站信息去估计基站位置方法的启发，考虑到室内外无缝定位中的坐标基准统一问题，本文提出室外利用GNSS辅助室内UWB基站位置估计的方法：首先选取基站平面坐标作为状态量，UWB 测距值和移动站坐标作为观测信息，在室外区域由移动站获取GNSS 坐标；再通过测距获取移动站到室内各个UWB基站的距离信息，建立状态方程和量测方程，得到基站位置估计的扩展卡尔曼滤波（extended Kalman filtering,EKF）模型。

1 算法原理

方法的总体方案是：在室外区域利用携带GNSS 坐标的移动站以一定的轨迹进行运动，同时获取室内区域各个UWB基站到移动站的距离。基站位置估计方案如图1 所示。

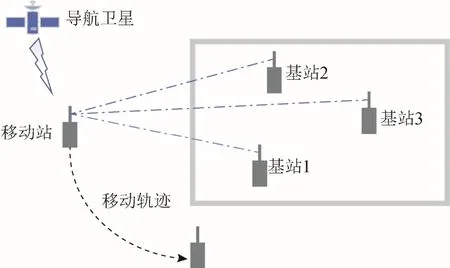
图1 UWB 位置估计

利用移动站坐标融合自身到基站的距离信息，加入EKF 模型进行紧组合，组合的模型如图2 所示。图中：di表示第i个基站到移动站的距离；(xs,ys)表示移动站坐标；(x i,yi)表示第i个基站坐标。

图2 基站位置估计组合模型

1.1 状态方程

选取基站的平面位置为状态量，并且设

式中：m为基站个数；Xi为第i个基站坐标，Xi=[xi yi]，0≤i≤m。

考虑基站在过程中保持静止，状态转移矩阵为单位矩阵，噪声驱动矩阵为对角矩阵，因此系统的状态方程为

式中：X(k)和X(k−1)表示前后2 个时刻的状态量；Φ(k/k−1)表示状态转移矩阵；Γ(k−1)表示k− 1时刻噪声驱动矩阵。并且有：

式中：I(2m)表示对角线元素为2m的单位矩阵；m为基站个数；T为采样间隔。

W(k)表示状态方程的过程噪声，它的均方根为

式中w为一个可调节的参数，w≪1。

1.2 观测方程

选取移动站到基站的距离值作为观测量，并且设

式中Zm为第m个基站到移动站的观测量。根据平面上2 个点的距离公式，有

对式（4）进行线性化并得到相应的雅可比矩阵

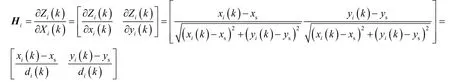
式中d i(k)表示k时刻的距离分量。联立观测量Z1～Zm，得到系统的量测方程为：

式中

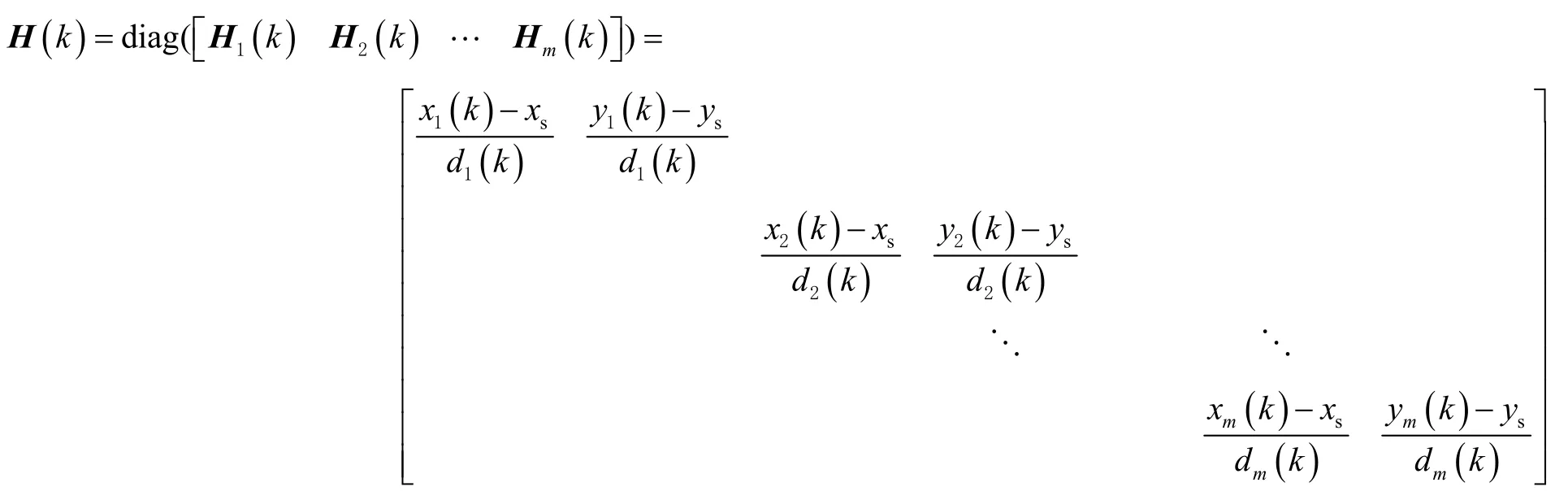
1.3 EKF 位置估计模型

通过以上公式推导，得到基站位置估计模型的状态方程和观测方程，并且通过对观测方程进行线性化和微分处理后得到雅可比矩阵H(k)。结合离散型线性化卡尔曼滤波方程组[10]，EKF基站位置估计模型的量测更新过程如图3 所示。

图3 EKF基站位置估计模型

2 实验与结果分析

2.1 仿真实验

利用矩阵实验室（MATLAB）软件对基站位置估计模型进行实验。选取平面上的3 个基站和1 个移动站，移动站轨迹坐标和移动站到3 个基站的距离值由仿真生成。给定基站真值坐标如表1 所示。

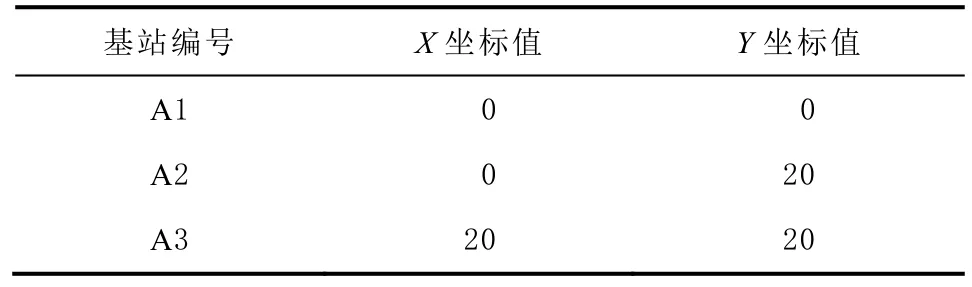
表1 基站真值坐标 m

移动站轨迹和基站坐标分布如图4 所示。

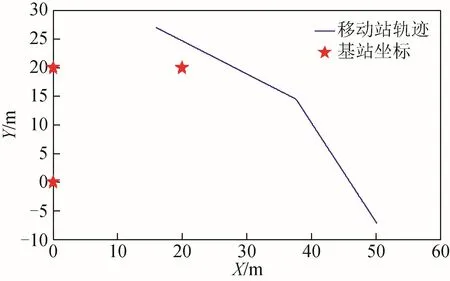
图4 移动站轨迹和基站分布

仿真实验中，初始值和参数选择为：

式（8）中δs表示移动站在2 个坐标方向上叠加的随机误差，是单个方向的标准差，取δs=1 m。将上述初始值和参数代入基站位置估计模型中，对估计结果进行处理后，得到3 个基站在X、Y方向上的估计误差，如图5～图7 所示。

图5 基站1 坐标估计误差

图6 基站2 坐标估计误差

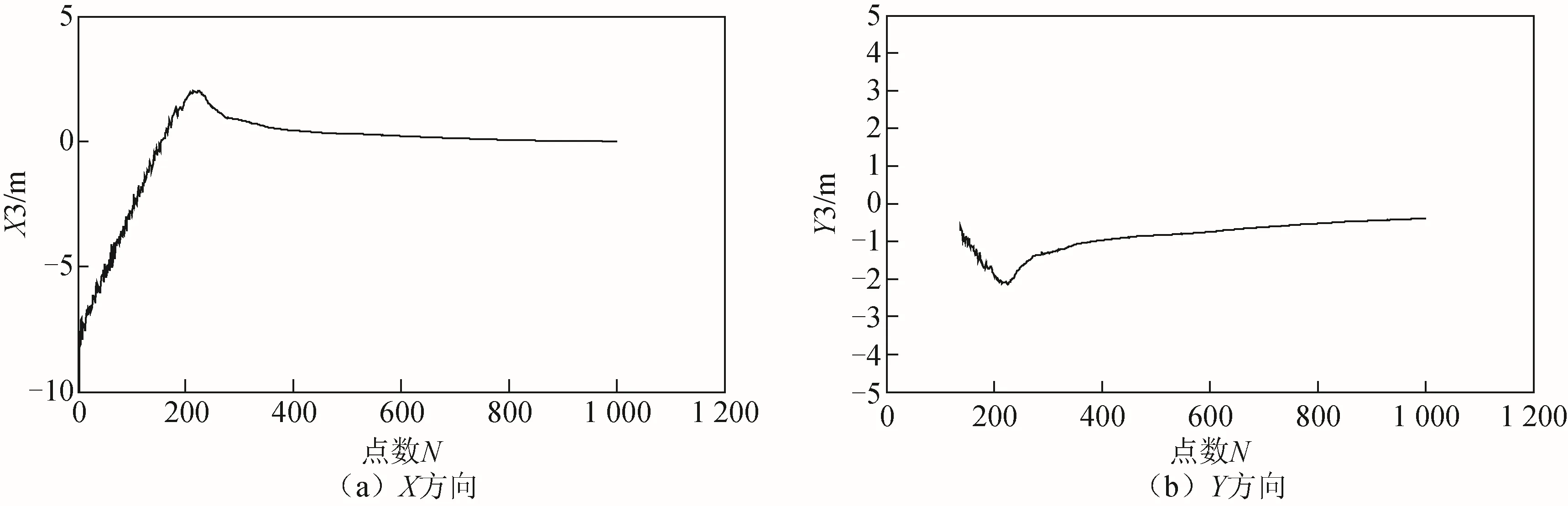
图7 基站3 坐标估计误差

利用均方根误差（root mean square error,RMSE）作为估计精度的评判标准。RMSE的计算公式为

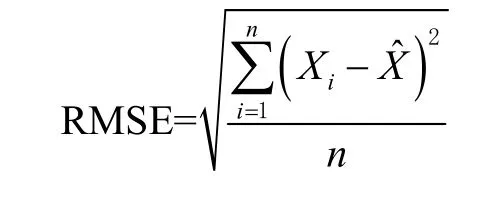
3 个基站在X、Y方向上的均方根误差如表2所示。

表2 基站坐标均方根误差 m

仿真结果表明，在给定移动站平面位置2 个方向上标准差为1 m的随机噪声，经过模型估计和解算后，3 个基站的平面坐标在2 个方向上的均方根误差都要小于1 m，最大误差为0.726 7 m，最小误差为0.159 1 m，估计效果良好。

2.2 实测

使用4 个UWB 定位标签、1 个NEO-7M 型号GNSS 接收机模块、1 辆机器人小车、1 台笔记本电脑组成实验平台。由GNSS 接收机模块获取经纬度坐标，坐标系选取 1984 世界大地坐标系（world geodetic coordinate system 1984,WGS84），利用文献[11]中的坐标投影公式将GNSS 坐标转换为通用横轴墨卡托（universal transverse Mercator,UTM）投影平面坐标，采样频率10 Hz；用3 个UWB 标签当基站，接收机和1 个UWB 标签当移动站获取距离值，获取的斜距可换算成平距，测距采样频率10 Hz。利用程序对电脑进行授时，保证GNSS 坐标和UWB 测距值输出时间同步。UWB 标签和移动站如图8、图9 所示。

图8 UWB 标签

利用千寻CORS（连续运行参考站系统）提供的高精度位置差分服务获取基站坐标[12]，基站真值坐标及其UTM 投影坐标如表3 所示。

表3 基站真值坐标及其UTM 投影坐标

移动站获取的GNSS 坐标同样利用UTM 投影公式转换为投影平面坐标。为防止计算量级过大带来影响，对每个移动站坐标减去初始点UTM 坐标，得到移动站轨迹和基站坐标的分布，如图10 所示。

图10 移动站轨迹和基站分布

实测的初始值和参数设置与仿真实验一致，并取δs=2 m。代入基站位置估计模型中，对估计结果进行处理后，得到3 个基站在X、Y方向上的估计误差，如图11～图13 所示。

图11 基站1 坐标估计误差

图12 基站2 坐标估计误差

图13 基站3 坐标估计误差

3 个基站X、Y方向上的均方根误差如表4 所示。

表4 基站坐标均方根误差 m

实测结果表明，利用室外GNSS辅助UWB基站位置估计方法能够有效地估计UWB基站平面位置，在假定GNSS 坐标存在2 m的随机噪声时，模型估计的结果能将基站平面2 个方向上的误差削弱到米级左右，最大方向上均方根误差为1.380 9 m，最小为0.510 4 m。

3 结束语

本文提出了GNSS辅助UWB基站的位置估计方法，选取基站平面坐标为状态量，对移动站的GNSS 坐标和UWB 测距值进行紧组合，使用EKF对基站坐标进行解算。通过仿真和实测实验对方法进行验证，结果表明方法具有较好的估计效果：仿真实验中基站坐标在2 个方向上的均方根误差在1 m 以内；实测实验中基站坐标在平面2 个方向上的误差在1 m 左右，最大为1.380 9 m，最小为0.510 4 m。该方法解决了在GNSS/UWB 组合的室内外无缝定位系统中室内定位基准与GNSS 坐标基准不一致的问题——UWB基站无须提前布设，自然统一到大地坐标系下，可为室内外无缝定位提供参考。