曲面拼接光顺方法研究

苏红磊 雍耀维 王婷 马维

【摘  要】依据A级曲面的几何连续条件，论文从控制点入手对曲面拼接的连续性进行分析。对于大曲率半径的简单曲面拼接，曲面分段的方法可以有效地提高曲面连续性调整效率和质量;对于复杂的小曲率半径多面拼接，从特征线入手，创建基础曲面，与相交的过渡面倒圆角，再合理地划分曲面片，确保曲面拟合精度和曲率连续过渡。经过实际应用表明，合理地设置控制点，从特征线开始构面，再以圆角面为基础进行曲面拼接，有效地提高了曲面光顺效率和质量，可以得到良好的品质。

【Abstract】According to the geometrical continuity condition of class A surface， this paper analyzes the continuity of surface stitching from the control points. For simple surface stitching with large radius of curvature， the segmented method can effectively improve the efficiency and quality of surface continuity adjustment. For complex multi-surface stitching with small radius of curvature， the basic surface was created from the feature line， and the intersecting transition surface was filled-off， and then the surface pieces were divided reasonably to ensure the fitting accuracy and continuous transition of curvature. The practical application shows that the reasonable setting of control points， starting from the feature line， and then using the rounded surface as the basis for surface stitching， can effectively improve the surface smoothing efficiency and quality， and can get good quality.

【關键词】曲面分段;控制点;圆角面

【Keywords】surface segmentation; control point; fillet face

【中图分类号】U463.82                                             【文献标志码】A                                                 【文章编号】1673-1069（2021）09-0177-05

1 引言

汽车曲面品质是影响汽车外观设计以及汽车性能的一个重要环节。车身的A级曲面，是指汽车车身外表面中的高可见区域，包括发动机引擎罩、车门、后背门、顶盖、前后翼子板、前后保险杠等。在A级曲面重构过程中，如何构建曲率连续的拼接曲面是难点。目前，对A级曲面的研究主要从精度和光顺2个方面进行。陈廉清等人（2006）提出自由曲面的控制点数量对曲面重构精度有很大影响，控制顶点的增加，控制网格相应增加，曲面拟合精度提高，没有结合光顺性。孔令德等人（2020）采用NURBS插入节点技术作为实现曲面细分建模，解决了建模中曲面裁剪与拼接的问题，数值计算稳定，算法简单，并可部分细分，但更适合于CG动画和雕刻曲面的设计。王鹏等人（2019）针对汽车车身拼接曲面光顺方法进行研究，提出不同曲率半径拼接曲面的光顺方法，在建模过程中，对曲面阶数的选取进行概括性总结，没有进行深入分析。

本文以Bezier曲面为研究对象，针对现有研究情况，从曲面阶次和控制点的角度，对其合理性进行理论分析，为构建曲率连续的拼接曲面奠定基础。同时从双面拼接和多面拼接的三面圆角、渐消角以及翼子板入手，从光顺实践的方向给出了更具操作性的方法。

2 曲面连续几何条件

2.1 Bezier曲线

Bezier曲线由端点和控制顶点组成，通过修改点的坐标可以改变曲线的形状，使用Bernstein多项式来表示：

其中，Bi，n（u）=ui（1-u）n-i是Bernstein多项式，是构成Bezier曲线的基本函数;Pi（i=0，1，…，n）构成了曲线的特征多边形，为曲线控制多边形的n+1个控制顶点。n表示的是曲线的阶数。增加了一个控制顶点后，定义同一条曲线的新控制点为Pi（i=0，1，…，n+1），则在保持曲线形态不变的情况下，可以增加控制点提高曲面阶次，升阶公式为：

曲线升阶后，增加控制顶点调整曲线，2个端点位置不变，因此，灵活度更强。应用升阶的方法，可以把曲线的阶次提高，升阶后的特征多边形更靠近曲线，当n较大时，特征多边形对曲线控制减弱，因此过高的阶数只能造成计算的难度，一般不高于8阶。

2.2 曲面连续性

一般情况，在A级曲面光顺实践中，为了便于曲面调整，更好地实现连续要求，拼接边界处相邻曲面在拼接方向上，每个曲面控制顶点都有相同的数量，曲面的连续性就归结为曲线的连续性，可以通过曲率来体现。如图1所示，同一线条用Bezier和NURBS来表示，其曲率梳发生变化，Bezier曲线整体性和全局性较好，曲率梳变化较为平缓、波动小、品质较高，所以在A级曲面中使用Bezier曲线和Bezier曲面片。

设2条Bezier曲线L1和L2，2条相切曲线端点处曲率半径大小相等，密切面重合，曲率梳轮廓线有折角，首末端相拼接达到G2连续。曲线L1和L2的控制点列为Pi（i=0，1，…，n）和Qj（j=0，1，…，m），先要满足G0连续，即控制点重合Pn=Q0;同时，满足G1连续，曲线L1末端2个控制点Pn-1、Pn与曲线L2首端2个控制点Q0、Q1共线，Pn-1、Pn=Q0、Q1顺序排列，即Pn-1-Pn=k（Q0-Q1），且有公共曲率，副法线向量相同：

式中，？驻Pn-2=？驻Pn-1-Pn-2、？驻Pn-1=Pn-Pn-1、？驻Q0=？驻Q1-Q0、？驻Q1=Q2-Q1为控制点的差分矢量，则Pn-2、Pn-1、Pn=Q0、Q1、Q2六点有公共密切面，Pn-2、Q2在其余顶点的公切线同侧。从控制点角度来看，拼接处曲率是由Pn=Q0处左右相邻3个控制点来决定的，即连接处曲率受左右共6个点影响，在Q0和Q1连线方向上移动Q2，端点曲率不变，只影响内部曲率分布。因此，G0两点重合，G1四点共线、G2六点共线、G3八点共线，调整曲面时，一般采用从低阶开始逐步增大，不超过8阶。

3 曲面拼接

产品外形一般比较复杂，要根据形体特征分割为多个面，曲率变化大的地方要用较多曲面表达，曲率变化小的地方应该尽量避免分割。为使数据满足外观和设计要求，曲面间需要达到必要的拼接连续性要求。曲面类零件按设计等级的不同。通常划分为4种连续等级，分别为：G0（位置连续）、G1（切线连续）、G2（曲率连续）、G3（曲率变化率连续）。拼接公共边界处的位置连续误差δG0≤0.002 mm，相切连续误差δG1≤0.02°，曲率连续误差δG2≤0.2mm-1。在曲面光顺中，控制顶点的排列对曲面拼接的质量和效率有极大影响。

3.1 简单曲面拼接

对于大曲率半径的拼接曲面，曲面相对比较平坦，如图3a所示。2个曲面片连接处有缝隙，要实现2个曲面曲率连续，就要保证有公共的边界，首先满足位置连续，再实现相切连续，并在公共主曲率下曲率主方向保持一致。控制点分布要均匀，曲率大的区域曲面控制顶点密集一些，曲率小的区域曲面控制顶点稀疏一些。从前面的分析得出，曲面阶数，过大不利于光顺，因而从4阶开始，最终不大于8即可，控制点排列要整齐。公共边界处，控制点部分不重合，逐一调整控制点会带来较大波动，所以先整排再单个，缩小连接缝隙，再重点调整圈中突变较为明显的控制点，调整完成，进行2个曲面片的匹配，公共边线实现重合如图3b。

从控制点来看，有突变，影响曲面间的曲率连续，观察曲率梳（见图4），曲率梳轮廓线基本重合，高度不一致，达到G0、G1连续，G2不连续，从图5b位置关系详细数据中，可以看出数值在0.160～0.573，与曲率梳判断情况保持一致。

采用增加曲面分段数的方法可以有效地改善曲面片的连续拼接情况，如图6所示，在不理想的区域增加分段边界，将左边曲面内部分割成为2部分，曲面阶数在U方向从以前的4增加到了6，再进行第二次匹配，控制点排列均匀很多，通过图5c曲面片2次匹配位置关系数据可以看出，G0、G1、G2、G3连续数据都有改善，效果较为明显。

结合曲面曲率梳断面，对控制点进行调整，具体看曲率轮廓线重合情况，并不能直接调整最靠近公共位置的控制点。先将红色曲率轮廓线调整重合，再沿着曲线切线方向微量调整，移动方向曲率增加，反之减小。反复多次调整，匹配最终完成如图7所示，从曲率梳过渡顺畅，轮廓线不存在折角，曲率连续，效果较好。

3.2 复杂曲面拼接

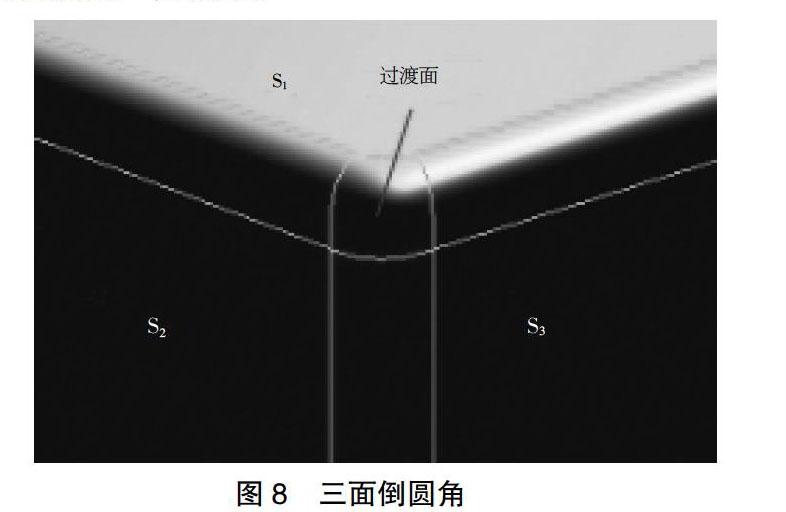
3.2.1 三面倒圆角

倒圆角在建模过程中是比较常用的一种方式，在G2连续的要求下，倒圆角也就变得比较复杂，尤其三面倒圆角，同样转化成为多面拼接的一种情况。如图8所示，S1、S2和S3为基础面，过渡面属于小曲率半径，所以在保证基础大面的贴合精度后，分别进行面圆角过渡，再构造过渡面轮廓特征线，轮廓线的精度直接影响最后曲面拼接精度。观察光照斑马线分析如图9所示，曲面拼接边界处P1、P2、P3、P4斑马线错开不连续，面与面之间只是边界重合，只达到了位置连续，需要对过渡面进行进一步调整。

检查过渡面拼接处位置连续误差如表1所示，不满足G0拼接连续精度要求。重新提取过渡圆角曲面拼接处的轮廓特征线，调整曲率梳，进行光顺处理，线、面剪裁，再根据边界轮廓生成曲面。调整过渡面的控制点由UV方向的5×4改为6×6，微调控制点，保证其排列整齐、顺畅，规律没有突点，最终完成如图10所示，斑马线过渡流畅、自然，满足G2的拼接连续精度要求。

3.2.2 渐消角

特征消失是一种常见的增加工业产品外表面动感的设计方式，应用广泛。在曲面重构过程中，也作为比较复杂的多面拼接形式进行处理。曲面重构时需要根据点云形状进行合理的曲面划分（见图11），在断面线上选取合适的点，将数据点通过插值或逼近拟合成曲线，构建特征线，再由线到面。

由特征线构建出基础面B1、B2和B3，再分别进行倒圓角处理，完成渐消角。B2和B3倒圆角得到圆角面A5，再根据四边轮廓线构建曲面片A4。通过曲率梳检查，拼接处曲率梳错位没有重合，表明公共点没有重合，如图12所示。需要重新对特征线进行修改，保持A4下边线端点的位置和切矢量关系，光顺后，投影至B2并剪裁，重新构建A4曲面。检查拼接边界处连续性精度：δG0 = 0.001mm，δG1 = 0.0124°，δG2 = 0.0034 mm-1，满足光顺精度要求。

最后对B1和B3之间进行倒圆角，得到A2和A3。对于A1、A2和A3，先调整好A2面，再完成左右相邻面的拼接。在进行调整时，UV方向阶数由4×4开始增加到6×6。控制点排列整齐，符合曲面造型趋势，并且与相邻面的控制点尽量保持一致，便于边界处连续处理。UV方向阶数一般不大于8×8，如图13所示控制点为10×6，中间区域点异常凸起，曲面明显起包，但是边界处控制点影响很小。因此，阶次增高虽然能增加曲面重构精度，但是过高对曲面的光顺性不利。渐消角部分最终调整完成的光照斑马线如图14所示，斑马线过渡自然流畅，达到G2连续要求。

3.2.3 翼子板曲面拼接

某车型翼子板如图15所示，沿着特征线划分所需曲面，构造符合造型趋势，较为规则的曲面片，大体分为S1、S2和S3三部分。以断面线为基准拟合曲线创建曲面，在拟合断面线时，尽量用一根曲线，如果拟合精度不高，可以采用分段的方式。为更好地保证曲面质量，通常先做基础大面，精调阶段再进行曲面分块，提高拼接质量，最终完成曲面片的逆向重构。在曲面构建过程中，曲面片需要多次调整以达到连续要求，控制点从4阶开始逐渐增加到6、8阶，曲面间相互交替调整。

在调整过程中，为保证过渡曲面的光顺质量，曲面间各个边界轮廓线要对齐，划分要规整，曲面片调整到8阶还不能达到较好的拼接质量，则需要进行曲面分片。曲面S2曲率变化较小，但面积相对较大，将S1和S2进行曲面划分，以达到更好的拼接质量。检查拼接后曲面贴近点云的精度最大偏差为0.1028，边界处连续性精度：δG0 = 0.000mm，δG1 = 0.0102°，δG2 = 0.0005 mm-1，满足光顺精度要求。

曲面S3根据特征线做面，相交面倒圆角。曲面S3与S2拼接处，以S2面的各个分块曲面边界线为起始点，画线进行分割，如图16a所示。调整时，一般把靠近外轮廓边缘的曲面作为基础面，中间为过渡曲面，更有利于提高拼接效率。把中间过渡分块曲面f1在U方向的控制点调整为8，观察S2和S3拼接处斑马线如图16b所示，线条发生错位，没有达到G2连续要求，还需要进一步调整。

f1曲面在8阶情况下，依旧不能很好地保证拼接质量，则需要对曲面片进行分片处理，沿着边界线交点A和B开始向对面边界做线，要尽量保证与相交线的切线方向垂直，有利于曲面进一步地调整。实际工程应用中，也时常提取边界曲线进行光顺处理，再用边界曲线进行曲面剪裁，重新构造曲面。最终完成翼子板逆向重构如图17所示，根据斑马线光照图可以看出，线条过渡均匀、自然、流畅，品质较高，达到G2连续要求，检查拼接后曲面贴近点云的精度最大偏差为0.3015，边界处连续性精度：δG0 = 0.000mm，δG1 = 0.0202°，δG2 = 0.0016 mm-1，满足光顺精度要求。

4 结语

为提高A级曲面的曲面拼接质量和效率，从简单双曲面到复杂多曲面2个方面进行了论述，针对曲率大的简单曲面拼接，采取曲面分段的方式可以快速得到高质量曲面;对于复杂的小曲率半径的曲面，从特征线入手，以基础曲面和过渡曲面的圆角面为基础结合轮廓线进行曲面拟合。在连续性调整过程中，曲面的阶次如果达到8还不能满足要求，则需要进行曲面分片处理，尽量避免分片曲面边缘出现尖角。实际应用表明，该方法可以提高曲面光顺效率和质量，获得良好的品质。

【参考文献】

【1】李和.汽车曲面品质分析及光顺优化方法研究[J].制造业自动化，2011，33（02）：114-115.

【2】陳廉清，王龙山，王乔冠.基于NURBS自由曲面重构的精度分析[J].农业机械学报，2006，37（3）：130-133.

【3】孔令德，康凤娥.NURBS曲面细分建模技术的研究与实现[J].洛阳师范学院学报，2020，39（5）：26-31.

【4】王鹏，徐家川，孙凯，等.汽车车身拼接曲面光顺方法研究[J].汽车技术，2019（2）：53-57.

【5】武镇锋，朱黎.空间曲面连续性的分类及其数学解释[J].机械设计，2011，28（2）：5-7.

【6】于济业，徐家川，李迪，等.汽车车身曲面光顺中控制顶点的排列[J].汽车技术，2011（7）：51-54.

【7】徐家川，薛远水，宋增祥，等.曲率对车身A级曲面控制顶点排列的影响[J].汽车技术，2013（09）：13-16.

【8】Dejun Liu 1.2 1.Mathematical Institute Beihua University Jilin China 2.Department of Mathematics Chengdu Armed Police Command College Chengdu China Fushun Gao Mathematical Institute Beihua University Jilin China. The G～1 Smooth Connection Algorithm between Biquartic B-spline Patches[A]. IEEE Beijing Section，China、Shanghai Jiaotong University，China、Xiamen University，China.Proceedings of 2009 IEEE International Conference on Intelligent Computing and Intelligent Systems（ICIS2009） Vol.3[C].IEEE Beijing Section，China、Shanghai Jiaotong University，China、Xiamen University，China：IEEE BEIJING SECTION（跨国电气电子工程师学会北京分会），2009：5.

【9】Shi Xiquan，Zhao Yan.G1continuity conditions of bicubic B-spline surfaces[J].Journal of Computer-Aided Design&Com-puter Graphics，2002，14（7）：676-682.