一种加速时间差分算法收敛的方法

何斌 刘全,2,3,4 张琳琳 时圣苗 陈红名 闫岩

强化学习是机器学习领域中最接近人类和动物学习的方法[1],在机器人自主决策和学习、复杂动态系统的优化控制和自动驾驶等领域中有着广泛的应用[2−5].强化学习算法分为基于模型和无模型两种.基于模型的算法需要一个精确且完整的环境模型,而无模型算法没有这个要求.无模型的强化学习算法中基于值函数的算法较为常用.该算法需要根据值函数得出最优的策略.如果值函数无法准确地被评估,或者评估的效率过低,那么将得不到最优的策略,或者耗时过长.所以,一个精确和高效的值函数评估方法对于基于值函数的强化学习算法至关重要[6−7].

对于值函数评估问题,经典的解决方法是TD(Temporal difference methods)算法和MC(Monte Carlo methods)算法.其中,TD 算法可以像动态规划(Dynamic program)方法一样使用自举(Bootstrap)的方式,即利用已经评估过的状态值来进行新的评估.这也使得TD 算法可以不需要等待情节结束,就可以进行值函数的更新,从而实现了在线学习的方式.MC 算法必须等到情节结束后才能进行值函数的更新,因而只能使用离线学习(Offline)的方式[1].但是如果TD 算法所利用的评估过的状态值有偏差,那么评估的结果往往在真实值附近.另外,TD 算法的收敛效率很大程度上取决于初值和步长参数的设定.优秀的初值和恰当的步长参数可以极大地缩小所需要策略迭代的次数,但是初值的设定往往需要丰富的经验和相关领域的专业知识.对于步长参数设定的问题,有许多自动设置步长参数的算法可以解决[8−9].然而,尽管这些算法有许多理论上的优势,但是由于其自身的复杂性和进一步增加了TD 算法的时间复杂度而得不到广泛的运用,实际应用中更多地采用固定步长参数的方法[10].这也就造成了加速一个特定TD 算法收敛速率的方法的匮乏.

论文提出的ATDMC 方法是利用MC 算法的无偏的性质,在TD 算法完成一次值函数评估后,进行值函数改进.即在广义策略迭代中加入减少值函数和真实值函数的之间距离的步骤,使得在不改变TD 算法的在线学习的方式基础上,加速算法的收敛.

文中第1 节描述了强化学习的相关基本概念和所用到的符号的定义.第2 节给出TD 算法的收敛速率的分析和ATDMC 方法的详细推导过程.第3节用实验分别展示在同策略评估、异策略评估和控制三个方面的加速效果.最后一节给出结论和后续的工作方向.

1 强化学习相关基本概念

1.1 马尔科夫决策过程

马尔科夫决策过程(Markov decision process,MDP)是研究各种强化学习算法的理论基础,可以对大多数强化学习问题进行建模[11].这是因为MDP 是在交互过程中学习以期达到某种目标的问题的框架,而强化学习问题是指如何在和环境交互过程中使得收到的累计奖赏最大化的问题.其中,学习和决定动作的对象称为智能体(Agent),智能体交互的对象为环境.

MDP 是由一个4 元组 (S,A,R,P) 构成.其中,S是指智能体在和环境进行交互过程中,环境的所有状态构成的集合.A是指智能体采取的动作构成的集合,收到的奖赏构成的集合为R.P是由状态转移函数构成.智能体和环境的一次交互是指智能体采取一个动作(Action)后,环境返回一个奖赏(Reward),然后智能体对环境进行观测,得到一个新的状态(State).为了表述简单,将一次完整的交互定义在时间步t发生,智能体所处的状态记为S t,采取的动作记为At,获得的奖赏记为Rt+1,到达的下一个状态记为St+1.将由时间步 0 到终止时间步T的整个过程称为一个情节(Episode).可见,一个情节中智能体经过的状态、采取的动作和获得的奖赏构成了一个序列:

将其中的奖赏的累计求和称为累计奖赏.从状态S t开始,直至结束状态S T获得的累计奖赏定义为:

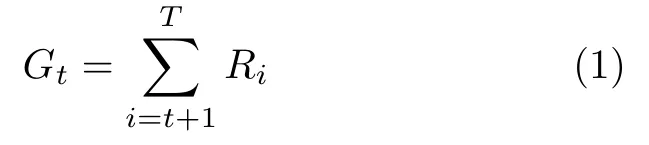
在一些强化学习任务中,最近获得的奖赏往往被赋予更大的权重值.因为相比于过去获得的奖赏,新的奖赏更值得关注.另外,当情节的时间步较长时,Gt将会变为一个比较大的值.对此,往往需要对获得的奖赏乘上一个折扣因子γ,来控制Gt的大小,则:

可见,如何使Gt最大化的问题即为强化学习在MDP 框架下所要解决的问题.

1.2 广义策略迭代

广义策略迭代(Generalized policy iteration,GPI)是强化学习中最一般的思想,几乎所有的强化学习算法都可以描述成广义策略迭代的形式.强化学习算法所要最大化的目标G t的值是由在各个状态下采取的动作决定的,而在某个状态采取何种动作是由策略决定的.强化学习的目标即为寻找一个策略使得Gt最大化,GPI 对此提供了具体思路.

GPI 可以分为策略评估(Policy evaluation)和策略改进(Policy improvement)两部分,由这两部分交替进行从而实现该思想.其中,策略评估是指在一个特定的状态下,对遵循一个固定策略的智能体将会收到的累计奖赏的期望进行估值.对于一个给定的策略 π,从t时间步开始,获得的累计奖赏的期望记为:

这个值被称为状态S t的v值,也称为S t在策略π的真实值.相应地,如果在时间步采取的动作为A t,那么获得的累计奖赏的期望为:

这个值也被称为状态动作对 (S t,A t) 的q值.由v值和q值的定义可知:

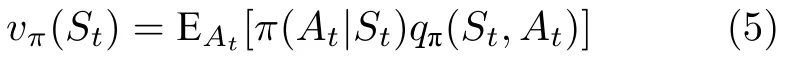
其中,π(A t|S t) 是在状态S t采取动作At的概率.

策略评估后,会根据评估出来的q值函数进行策略改进.策略改进一般采用ϵ-greedy 算法,即最大的q值对应的动作被选取的概率为 1−ϵ,另外有ϵ的概率任取一个动作.一次策略评估和策略改进形成了一次完整的策略迭代.下一轮迭代将根据新的策略继续评估,然后再改进策略.经过多次策略迭代后,策略达到了稳定的状态,各个状态的值函数达到最大值.此时的策略称为最优策略,对应的值函数称为最优值函数,记为

1.3 TD 算法

TD 算法是强化学习中最核心的算法,可以用来评估v值和q值函数.如果一些状态的值函数已被评估过或是被赋予了初值(虽然初值可能是错误的,但也可以视为被评估过),则可以利用这些评估过的值来评估其他状态的值函数.TD 算法会对每一个v值或者q值进行赋初值,再利用这些初值进行新的评估,然后进行策略改进,不断循环进行从而实现GPI.

TD 算法策略迭代的过程可以看作是值函数不断向v⋆靠近的过程.在具体的TD 算法中,v⋆是未知的值,往往被替换成相应算法的目标UTD.根据所利用的评估过的值函数是一步还是多步之后的状态的值函数,将TD 算法分为一步或n步TD.对于n步TD 算法而言,UTD为:

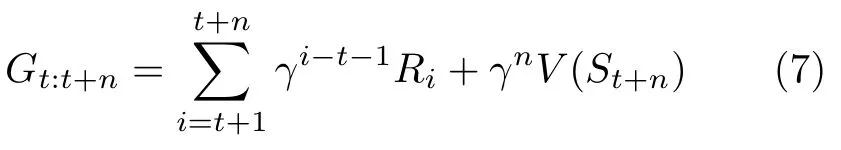
其中,V(S t+n) 为n步之后的状态的v值的估计值,而这个值可能是错误的.如果该值为对应状态的真实值,则显然Gt:t+n的期望也为真实值.另外,n=1的情况即为一步TD 的UTD.利用n步TD 算法的目标,TD 算法的值函数的更新公式为:

其中,α为步长参数.

强化学习在处理状态空间很大的问题时,往往采用函数逼近的方法.使用状态的特征向量x(S t)和权重向量w来表示状态的值函数.在使用线性逼近方法的情况下,值函数记为:

显然在函数逼近的条件下,并不一定存在一个权重向量w使得所有状态的值都能等于对应的vπ.所以,为了求出使得值函数和vπ之间的距离的平方和最小的w,将损失函数定义为:

由于vπ(S t) 值未知,将其替换为UTD. 那么TD算法的权重向量的更新公式定义为:

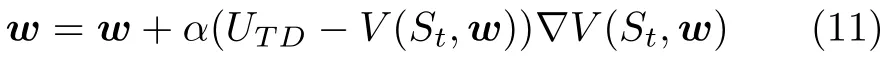
1.4 MC 算法

MC 算法是另外一种强化学习中评估值函数的算法.MC 算法的值函数的更新公式为:

其中,n是情节数.从公式可见MC 算法的目标为G t,而由Gt的定义可知Gt的值是整个情节中所有的奖赏的累计和.也就意味着如果情节不结束,Gt的值都是未知的,从而使得MC 算法只能使用离线学习的方式.

从vπ的定义可知MC 算法的更新目标G t的期望值为vπ,即Gt是vπ的无偏估计.而TD 算法的目标只有在V(S t+n) 为真实值的情况下,其期望值才等于真实值.再有,策略迭代开始时V(S t+n) 的值都为初值(往往都被设为0),距离真实值较远.所以在初期,MC 算法的更新量Gt −V(S t) 是大于TD 算法的更新量.另外,对于使用步长参数 1/n的MC 算法和使用固定步长参数的TD 算法,它们步长参数的不同也使得策略迭代初期MC 算法的收敛速率更快.

2 ATDMC 方法

本节将通过分析得出影响TD 算法收敛速率的因素,然后通过减少这些因素的影响来加快TD 算法的收敛速率.

2.1 TD 算法的收敛速率

任取一个状态S t,将其n+1 次更新后的估计值记为Vn+1,策略π下该状态的真实值记为vπ. 将V n+1值和真实值之间距离的平方的期望定义为误差en+1,则:

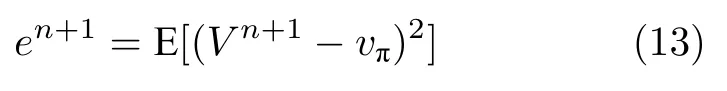
显然en+1减小到0 的速率即为TD 算法收敛的速率.将TD 算法的更新公式代入式(13),得

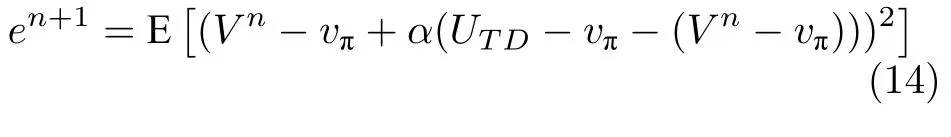
假定UTD的期望等于vπ,将式(14)展开得:

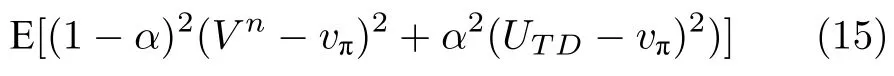
整理得:

进一步,展开得:

式(17)中e0是由初值所确定的,而UTD的方差则是由具体的TD 算法所决定的.随着α →0 且n →∞,en+1逐步变小,最后收敛到0.可见,收敛的速率是由步长参数、初值和TD 算法本身的性质三者共同决定的.在实际使用TD 算法时,往往采用固定的步长参数,en+1变为一个有上界的量.如果设置步长参数较小时,等式的第一项收敛到0 的速率较慢,第二项一直保持为一个很小的值,所以最终的收敛的效果是速率慢,但是很稳定.而如果步长参数设置较大时,第一项会很快收敛,第二项的值对算法的收敛速率起主要的影响作用,表现为虽然收敛速率快,但是波动程度大.这一点与调试步长参数的过往经验是一致的,只有当步长参数设置适中时,算法的效果才能达到最优.

对于一个给定的策略和一个固定的步长参数条件下,如果想要加速TD 算法,D[U TD] 对于给定TD 算法是无法改变的,那么只有减少e n.虽然e0是由初值确定的,但是e1,e2,···等都是可以减小的.

2.2 TD 算法的目标

在第2.1 节中,论文假定UTD的期望等于vπ,而在策略迭代初期该条件是不满足的.实际上,在一个给定策略下,一个情节中不同时间步的同一状态的TD 算法的目标UTD构成了一个不稳定的序列(A non-stationary series).即在收敛之前,U TD的期望值一直在变化,直至收敛后,UTD的期望才能达到稳定状态.假设所有状态初值都为0,奖赏都为正时,构成的序列如图1 所示,图中的点是U TD的估计值,图中的线是由UTD的期望构成.这也说明在策略迭代初期,各个状态的值和UTD之间的距离较小.并且加上步长参数的作用,使得初期的收敛速率较慢.但是MC 方法的目标是一个稳定的序列,其期望值始终等于vπ.如果采用MC 算法的目标作为再次更新的目标则可以减小e n,从而加速收敛.

图1 由 UTD 构成的不稳定序列Fig.1 A non-stationary series

2.3 ATDMC 方法的推导过程

根据前面两节的分析,TD 算法在策略迭代初期收敛速率慢的问题可以通过减小e n来解决.而MC 方法的目标在策略迭代初期相较于TD 算法的目标距离真实值更近,可以借助其来减小en. 对此,在一般的GPI 中加入值改进的步骤,使得e n减小.改进后的GPI 如图2 所示.具体的方式是在TD 算法更新完成后,再以MC 算法的目标作为新目标来更新.

图2 改进后的GPIFig.2 The improved GPI

为了再以MC 算法的目标进行更新,线性函数逼近的方式下,将损失函数定义为:

其中,w为经过TD 算法更新后的权重向量.对损失函数求w的偏导:

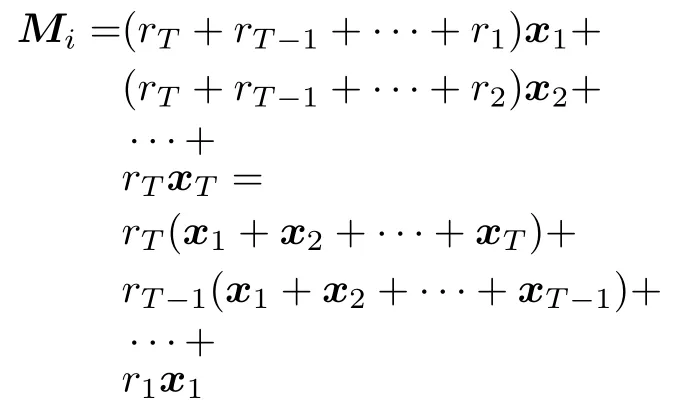
观察第二个等号后面的式子,可知r1x1可以在时间步1 求出,相应地r T−1(x1+x2+···+x T−1)可以在情节结束前一个时间步求出.再令P i则:

可见,使用均摊迹只需要保存两个变量P i和M i,然后在各个时间步不停地更新这两个值.最终ATDMC 方法的更新公式为:

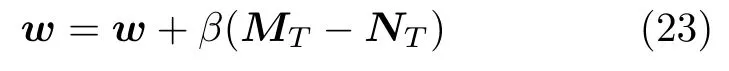
另外,M0、N0、P0都为 0向量.β为步长参数.式(20)、(21)和(22)在TD 算法更新完权重向量后执行,式(23)在情节结束后执行.这样并没有改变原TD 算法的结构,也就不会改变在线学习的方式.

在异策略学习中,由于目标策略和行为策略不一致,需要采取重要性采样方法来放大或缩小值函数.只需要将式(22)改为

其中,ρi为重要性采样因子.

3 实验及结果分析

本节将分别在同策略评估、异策略评估和控制三个方面进行实验,展示ATDMC 方法可以对多种TD 算法进行加速收敛,以及原TD 算法的步长参数α和ATDMC 方法的步长参数β对加速效果的影响.其中,策略评估的实验侧重覆盖多种TD算法,而控制的实验则更多的体现步长参数的影响.

3.1 同策略评估

博扬链(Boyan chain)是强化学习中用于比较不同TD 算法性能的问题[12].这个问题中一共有13个状态.其中,状态12 是开始状态,状态0 是终止状态.每个状态都有两个动作(状态1 两个动作都到达终止状态0),如图3 所示.除了状态1 到状态0 的奖赏是−2,其他收到的奖赏都是−3.状态12、8、4、0 的特征向量分别为[1,0,0,0]、[0,1,0,0]、[0,0,1,0]、[0,0,0,1].处于这些状态之间的状态的特征向量可以用插值法求得.例如,状态11、10、9 的特征向量分别为[3/4,1/4,0,0]、[1/2,1/2,0,0]、[1/4,3/4,0,0].所要评估的策略设定为每个状态的两个动作被执行的概率相等.

图3 博扬链Fig.3 Boyan chain

为了覆盖较多的TD 算法,用ATDMC 方法分别加速TD(0)、GTD[13]、GTD2 和TDC[14]算法.这4 种算法相比于其他的TD 算法(如LSTD、KTD和GPTD 等)收敛速率更快[15].另外,实验通过比较均方根误差(Root mean square of er r or,RMSE)的减小速率来体现ATDMC 方法的加速效果.RMSE是衡量TD 算法求出的值和真实值之间误差的常用指标.如果ATDMC 方法的RMSE 减小速率更快,则可以体现ATDMC 方法的加速效果.为了让步长参数的大小一致,原TD 算法和加速后的算法的步长参数α都设为0.5.如果算法存在次级权重向量,那么其对应的步长参数也都设为0.25.ATDMC 方法的步长参数β都为0.1.每个实验都是重复100 次取平均值,且折扣因子γ都为1,权重向量的初值都为 0 向量.

比较结果如图4 所示.图中实线对应原TD 算法,虚线是加速后的效果.可见,虽然各个TD 算法收敛速率不尽相同,但是都得到了加速.另外,ATDMC 方法利用MC 算法目标的无偏性质进行一次值改进后,误差就已经显著减少.

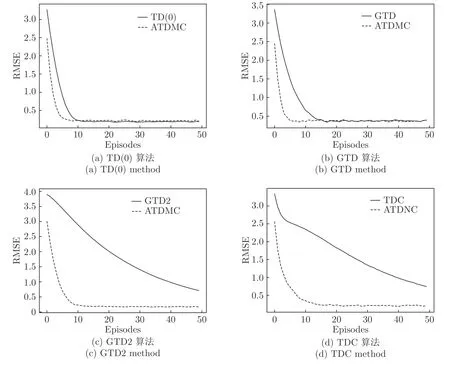
图4 同策略评估Fig.4 On-policy estimation

3.2 异策略评估

本节是在11 状态的随机漫步问题上做实验,并在一般的随机漫步问题上进行了修改[16],如图5所示.这个问题共有11 个状态,状态1 是开始状态,状态11 是终止状态,每个状态都有向左和向右两个动作,除了状态1 的向左的动作是到达自己外,其他的动作都是到达相邻状态.可以看出,由于向左和向右动作的作用使得实验一个情节的时间步数可能会很长.而较长的情节才能体现异策略评估算法的优劣性.前一节中的博扬链的情节最长为12 步,最短为6 步,不再适用于异策略评估,所以换为随机漫步问题.只有到达终止状态11 才能获得1 的奖赏.其他所有的奖赏都为0.特征向量是一个10维向量.状态1 的特征向量是前1维√为后面为0.状态2的特征向量是前2维为,后面为0,以此类推.状态11 的特征向量为 0 向量.评估的目标策略为采取向左的动作概率为0.4,采取向右的动作概率等于0.6.而行为策略采取向左和向右动作的概率相等.

图5 11 状态的随机漫步Fig.5 11-State random walk

资格迹是强化学习的重要方法[17−19].在异策略评估方面,TD 算法和资格迹相结合使得收敛速率和准确度都得到了提升.为了证明使用资格迹加速后,ATDMC 方法仍然可以加速,实验采用了TD(0)和GTD 算法的资格迹版本:TD (λ)[20−21]、GTD(λ)[22].另外,为了进一步覆盖更多的TD 算法,又选取了另外两种算法:HTD (λ)[23]和ETD (λ)[24−25].参数设置方面,λ都设为0.6,ATDMC 方法的步长参数β都为0.001.其他参数与同策略评估设置一致.每个实验也同样重复100 次取平均值.

比较的结果如图6 所示.可见,异策略评估方面采用资格迹的TD 算法的收敛速率也都得到了加速.需要特别指出的是异策略评估算法中HTD 的收敛速率最快,但是牺牲了准确度.ATDMC 方法在保证收敛速率不变的条件下,提高了HTD 算法的准确度.

图6 异策略评估Fig.6 Off-policy estimation

3.3 控制

山地车(Mountain car)和平衡杆(Cart pole)问题是强化学习控制方面的经典问题,许多算法都是在这两个问题上进行实验.关于这两个问题的细节在许多文献中有着详细的描述.另外,选用这两个问题还因为这两者的目标刚好相反,山地车问题的目标是小车尽可能快地到达山顶,平衡杆问题是尽可能久地保持杆子的平衡,一个是让一个情节的时间步数尽可能的少,而另一个让时间步数尽可能的多.

山地车问题采用的是sarsa (λ) 算法[26]来解决.为了体现算法收敛速率的快慢,实验只关心前50个情节的时间步数.前50 个情节的平均时间步数越短,说明收敛速率越快.实验采用了瓦片编码(Tile coding),选择动作的ϵ-greedy 算法的参数ϵ设为0.

为了展示相同步长参数β和不同的α对加速效果的影响,第一个实验固定β=0.0001,而sarsa(λ)算法采取不同的步长参数α,实验结果如图7 所示.纵坐标的步数是前50 个情节的时间步数的平均值.从图中看出当α较大时,β设为0.0001 没有加速,反而减慢了速率.当然在α较大时,sarsa (λ) 算法的效果也比较差,所以需要调整步长参数.当α较小时,虽然α不同但是都得到了加速.

图7 山地车问题 (β 固定)Fig.7 Mountain car(fixedβ)

接着,为了展现不同的β和同一α加速效果,α分别取了0.8/8、1/8、1.4/8 和2/8.结果如图8 所式.当α较小时,随着β逐渐变大,加速效果由逐渐变好再逐渐变坏.当α较大时,ATDMC 方法的并没有加速效果.这一点与其他强化学习算法一致,过大的步长参数将会使算法效果变差.

图8 山地车问题 (α 固定)Fig.8 Mountain car(fixedα)

第二个实验是平衡杆问题.平衡杆的每个情节的步长最大值为200,当连续100 个情节的平均步长大于195 视为该问题得到解决.易知,解决问题所花费的情节数越短说明算法收敛得越快.实验设计和山地车问题是一致的,但是采用的是一步sarsa 算法,选择动作的ϵ-greedy 算法的参数ϵ设为0.08.首先也是比较相同的β和不同的α的对加速效果的影响,固定β为0.0005.实验结果如图9 所示.接着也比较不同β和相同α的影响.α分别等于0.2/16、0.4/16、0.6/16 和0.8/16.实验结果如图10所示.图中纵座标是总共进行的情节数,其中最后100 个情节是验证问题是否解决,前面的情节是学习花费的情节.和山地车问题的实验结果相比,虽然实验内容不同,但是加速效果类似.

图9 平衡杆问题 (β 固定)Fig.9 Cart pole(fixedβ)

图10 平衡杆问题 (α 固定)Fig.10 Cart pole(fixedα)

从这两个实验可以看出在TD 算法步长参数α过大时,ATDMC 方法并没有加速效果.而当步长参数α较小时,可以实现不同程度的加速,但是还没有达到最好效果.只有当步长参数α适中时,ATDMC 方法的步长参数β也适中时,才能达到算法的最好效果.

4 结论和后续工作方向

针对加速特定TD 算法收敛速率的方法匮乏的问题,本文提出利用MC 算法无偏的性质来加速TD算法收敛的ATDMC 方法.通过分析TD 算法的收敛速率得出可以通过减小e1,e2,···来加速收敛,而MC 算法的目标可以在学习初期减小这些值,进一步推导得出了最终的方法.从推导过程可知,加速的实现并不需要改变原TD 算法,也即TD 算法的在线实现的方式不会被改变.同时,只引入了3 个额外的变量,并没有增加算法的空间复杂度.从实验结果可以看出,本文提出的方法可以有效地加速各类TD 算法,恰当的步长参数使得算法达到最优的加速效果.

另外,需要指出的是ATDMC 方法只适用于情节式任务.对于连续任务,有两种解决方案:一种是引入可变的折扣因子γ,在恰当的时间步设置γ等于0(相当于主动结束任务),从而转换为一个情节任务,但并不影响对应MDP 的流程;另外一种是采用平均奖赏设定(Average-reward setting),MC方法的目标需要重新用奖赏和奖赏的平均值的差值来定义.更多的细节需要进一步研究.