Observation of Internal Tides in the Qiongzhou Strait by Coastal Acoustic Tomography

CHEN Minmo, ZHU Zenan, ZHANG Chuanzheng, ZHU Xiaohua, 2), 3), *, LIU Zhaojun, and KANEKO Arata

Observation of Internal Tides in the Qiongzhou Strait by Coastal Acoustic Tomography

CHEN Minmo1), ZHU Zenan1), ZHANG Chuanzheng1), ZHU Xiaohua1), 2), 3), *, LIU Zhaojun1), and KANEKO Arata4)

1) State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography, Ministry of Natural Resources, Hangzhou 310012, China 2) School of Oceanography, Shanghai Jiao Tong University, Shanghai 200240, China 3) Southern Marine Science and Engineering Guangdong Laboratory (Zhuhai), Zhuhai 519000, China 4) Graduate School of Advanced Science and Engineering, Hiroshima University, Higashi-Hiroshima, Hiroshima 739-8527, Japan

In this study, power spectral density and inverse analyses were performed to obtain the frequency characteristics and spatial distribution of temperature in the Qiongzhou Strait using reciprocal sound transmission data obtained in a coastal acoustic tomography experiment conducted in 2013. The results reveal three dominant types of internal tides (diurnal, semidiurnal, and terdiurnal). Spectral analysis of the range-average temperature deviation along the northern and southern transmission paths shows that along the northern path, the energy of the diurnal internal tides was significantly larger than that of the semidiurnal tides. The semidiurnal internal tides, in contrast, were more pronounced along the southern path. A terdiurnal spectrum with an energy level equivalent to that of the semidiurnal internal tide was discernable for both the northern and southern paths. These three types of internal tides can also be recognized in the time variation of the zonal-average temperature deviation. The diurnal internal tides were strengthened along the northern coast, implying their westward propagation and the existence of coastally trapped effects. The other two types of internal tides, which have smaller wavelengths than the diurnal internal tides, were less resolved over the entire tomographic domain due to the insufficient resolution of the inversion. The data quality was verified to be satisfactory by error estimation.

coastal acoustic tomography; inverse analysis; diurnal internal tides; semidiurnal internal tides; terdiurnal internal tides;Qiongzhou Strait

1 Introduction

The Qiongzhou Strait, which connects the northern South China Sea in the east and the Gulf of Beibu (Gulf of Tonkin) in the west, is a passageway for tidal waves that intrude into the strait from both the east and west. The thermal and fishery environments of the coastal regions surrounding the strait and the thermal connection between the northern South China Sea and Gulf of Beibu may be controlled by these tidal waves and the associated internal tides. The tidal environments are characterized by the dominance of diurnal over semidiurnal tides (Shi, 2002; Zhu, 2014). The diurnal tides intrude into the strait from both the western and eastern entrances, whereasthe semidiurnal tides propagate eastward through the strait. Diurnal internal tides generated locally at the shelf break east of Hainan Island propagate westward and reach the eastern entrance of the Qiongzhou Strait (Xu, 2010;Zhao, 2018). Observation data obtained further north- east also indicate the propagation of a diurnal internal tide toward the shelf sea from the continental slope region (Duda, 2004). This propagation of the diurnal internal tides has also been simulated by a baroclinic ocean model (Bai, 2015). However, the propagation behavior of internal tides inside the strait has never been reported.A number of studies have been devoted to the generation of nonlinear tides in the coastal seas (Shengand Wang, 2004; Zhu, 2017a; Aruni, 2020). However, the non- linearityofthetidalsignalsremainsunknownintheQiong- zhou Strait due to the lack of observation data.

Coastal acoustic tomography (CAT), an application of deep-sea tomography (Munk, 1995) in coastal seas, is considered to be an innovative technology for mapping the 2D or 3D structures of current and sound speeds (which are mainly determined by temperature) (Kaneko, 2020). The coastal environment, which varies rapidly, can be measured by the snap-shot capability of CAT (Park and Kaneko, 2000; Yamaoka, 2002; Kaneko, 2005; Lin, 2005; Yamaguchi, 2005; Zhu, 2013; Zhang, 2015, 2017; Chen, 2017; Zhu, 2017b). In 2013, a CAT experiment was conducted in the Qiongzhou Strait to measure the tidal and residual currents and the volume transport through the strait (Zhu, 2015). The current fields inside the tomographic domain werereconstructedbytheinversionofthedifferentialtravel times. The accuracy of the current fields was validated against shipboard ADCP data, and the root-mean-square difference was determined to be as small as 3.5cms−1.

In this study, the internal tides are investigated using the mean travel time data obtained in the 2013 Qiongzhou Strait experiment. The observations are described in Section 2. The inverse method used to reconstruct temperature fields from the mean travel time data is described in Section 3. Observed internal tides are analyzed in Section 4, and detailed discussions are presented in Section 5,followed by our conclusions in Section 6.

2 Observations

A CAT experiment conducted in the Qiongzhou Strait from March 17 to April 1, 2013 included four CAT stations (C1–C4), which enabled the construction of six sound transmission paths (Fig.1). A detailed description of the experiment is provided by Zhu(2015). Using anchored fishing boats, the four CAT stations were deployed on the northern and southern sides of the Qiongzhou Strait, which surround the tomographic domain of 11.5km×16.5km. Due to tidal currents, the anchored boats rotated clockwise to draw a circle with a radius of approximately 100m. The ship movement was tracked us ing the global positioning system (GPS) of the CAT system. However, the accuracy of the GPS data was not sufficient due to the offsets between the positions of the GPS antenna and the subsurface acoustic transducer. As such, more precise transducer positions were calculated with errors of less than 3m for every sound transmission. This was achieved by taking the product of the variable CAT mean travel times and the fixed depth-average sound speedfrom the conductivity-temperature-depth (CTD) meter (Ka- neko, 2020).

Fig.1 Map showing the location of the Qiongzhou Strait and the measurement sites: (a), location of the South China Sea; (b), location and bathymetry of the Qiongzhou Strait, with the red and green arrows showing the propagation of diurnal (O1+K1) and semidiurnal (M2) tides, respectively; (c), location of the CAT experiment sites, where the four acoustic stations (C1–C4) are indicated by the red squares, and the transmission paths connecting each station are indicated by the red lines; the black dashed line connecting E and F indicates the north–south line where the meridional distribution and temporal variation of inverted temperature are examined in Fig.3; C indicates the conductivity-temperature-depth (CTD) cast point; the 5-km scale is shown in the lower right corner.

A 5-kHz sound modulated by an eleventh-order M sequence was simultaneously transmitted from each station every 5min. The temperature and salinity were measured using the CTD data in the center of the tomographic domain on March 24 and 28 to correct the ship positions, acquire reference sound speed profiles for range-independent ray simulation, and perform dynamic mode analysis. The original data obtained at 5-min intervals were band-pass filtered using 14–30h, 10–14h, and 6–10h bandwidths, respectively, to retrieve the diurnal, semidiurnal, and terdiurnal internal tides (the conventional terminology of tides with an eight-hour period).

Reciprocal travel times were determined at each station using the largest correlation peak corresponding to a ray traveling from the surface to a depth of 30m. As a result, the vertical temperature, salinity, and current profiles were not resolved in this study, although these targets were ac- complished in a previous paper for which multipeaks were available (Chen, 2017). The mean travel time data obtained along the six sound transmission paths were con-verted to range-average sound speeds. These data were fur-ther converted to range-average temperatures (RATs) using Mackenzie’s sound speed formula (Mackenzie, 1981), assuming fixed salinity and depth. The power spectral densities were then calculated using the hourly mean RAT.

3 Methods

3.1 Inverse Method

An inverse method for reconstructing temperature fields from observed mean travel time data was proposed by Huang(2019). Here we briefly describe this inversion method, which is based on the Fourier function expansion of the sound speed deviation. The-th refracted ray between acoustic stations A and B is projected to a horizontal slice. The mean travel time deviationδtfor the-th projected ray with horizontal lengthLis represented by:

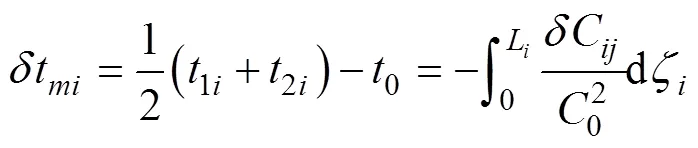
where1iand2idenote the travel time of the-th ray from A to B and from B to A, respectively.δCdenotes the sound speed deviation of the-th grid along the-th ray, dζdenotes the segmented length for the-th ray, and0and0i(=L/0) denote the reference sound speed and travel times, respectively.

δCis expanded into a Fourier series as follows:

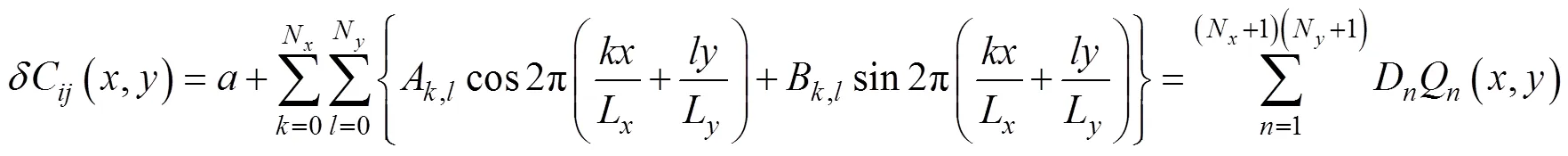
where (,) is the two-dimensional Cartesian coordinate, andLandLare the lengths of the tomographic domain in theanddirections, respectively.

is the vector of the unknown coefficients, and

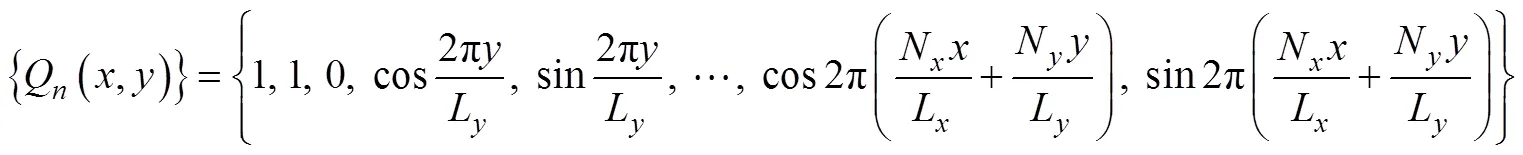
is the expansion function vector. Substituting Eq. (2) into Eq. (1), we obtain the following:

whereNandNdenote the total number of expansions in theanddirections, respectively. In this study, we usedN=N=2, so the total number of unknown variables became 19. Eq. (3) is solved using the tapered least-squares method with the L-curve method (Munk, 1995). The inverted sound speed was converted to temperature using the following formula for a fixed salinity of 32 and a fixed depth of 15m:

Thus, by repeating the above inversion process at each time step, a time series of temperature oscillations was obtained inside the CAT domain. These were used to analyze internal tides in the Qiongzhou Strait. Note that the mean spatial resolution of the inversion is 4.4km for the six transmission paths (Zhu, 2015).

3.2 Dynamic Mode Analysis

As indicated by Gill (1982), the basic equation for inertial gravity waves is as follows:

whereis the vertical velocity of fluid motion,is the Coriolis parameter, and

is the buoyance frequency. When the wavelength is much greater than the water depth, the inertial gravity waves reduce to long gravity waves, which propagate only in the horizontal direction. Thus, the solution to Eq. (5) can be expressed as follows:

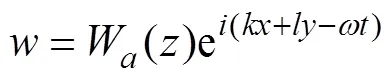
whereW() is the amplitude function, which depends on the depthand the wave frequency. By substituting Eq. (6) into Eq. (5) and neglecting the Coriolis effect, we have the following:

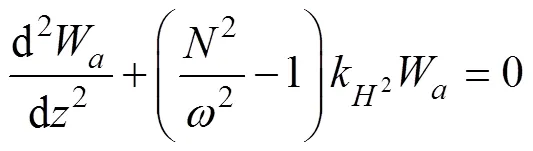
The set of Eqs. (7) and (8) constructs an eigenvalue problem, which means their solution is a finite number of normal modes.

4 Results

4.1 Range-Average Temperature (RAT)

Fig.2 shows the time series of the RAT deviations for the March 17–April 1 period, which were calculated along the southern and northern transmission paths (C1C2 and C3C4, respectively) from the range-average sound speed deviationsusingEq.(4).Thenorthern-pathdataweredomi- nated by diurnal oscillation, whereas the southern-path data, with higher frequency variations, were embedded within the diurnal oscillations. The amplitude of oscillation was approximately 0.7℃ for both sets of data. and the phase of oscillation showed adequate agreement between the two. The 25-h mean temperature showed seasonal warming from 20.6℃ to 22.3℃ during the entire period. Due to operational problems, data were missing for March 28 along the northern path and March 26–29 along the southern path.

Fig.3 shows the power spectral densities calculated using the hourly mean RAT deviation data in the period band from March 18 to 25 (Fig.2) for the northern (black) and southern (red) transmission paths. For the northern path, the diurnal peak was significantly higher than the semidiurnal peak. In contrast, the semidiurnal peak was more pronounced for the southern path than for the northern path. A terdiurnal peak was visible for both the northern and southern paths, with the peak height comparable to that of the semidiurnal tide. However, the peak heights for the southern path were higher than those for the northern path.

4.2 Inverted Temperature

Fig.4 shows the two-dimensional distribution of the inverted temperature deviations for the 14–30h band duringMarch 18–19 with a 3-h interval. The temperature data show a diurnal cycle. The east-west structures, which feature cores of warm and cold water in the central region, are visible around the mean waters (Figs.4b, 4f, and 4n) and are diminished around the high waters (Figs.4a, 4i, 4h, and 4p) and low waters (Fig.4d). The diurnal temperature oscillation is strengthened along the northern coast, in com- parison with that of the remaining region, ranging from-0.7℃ to 0.5℃. The diurnal temperature oscillation is ir- regular along the southern coast.

Figs.5 and 6 show the two-dimensional distributions of the inverted temperature deviations for the 10–14-h and 6–10-h bands during March at 3-h and 2-h intervals, respectively. The semidiurnal and terdiurnal temperature oscillations are visible in both Figs.5 and 6. In Fig.5, the temperature oscillated between the northern and southern regions. Except for Fig.5h, the northern regions arer wider than the southern regions, and exhibit a narrow zone in the northeast (Figs.5a, 5c, 5e, and 5g) and northwest (Figs.5b, 5d, 5f, and 5h) corners. Overall, the temperature oscillation in Fig.6 is nearly identical to that in Fig.5, except that the three zones in the northern, central, and south- ern regions exhibit a pronounced 8-h interval (Figs.6a, 6c, 6e, 6g, 6i, and 6k).

Fig.2 Time plots of the range-average termperature (RAT) for (a) the northern (C3C4) and (b) southern (C1C2) transmission paths. Red dots indicate the original 5-min interval data; solid black and blue lines indicate the hourly mean data and 25-h mean data, respectively; the time band used in the spectral analyses is bounded by the blue dashed lines.

Fig.3 Power spectral density diagrams for the range-average temperature (RAT) deviation along the transmission paths C1C2 (red solid line) and C3C4 (black solid line).

The inverted temperature deviations were zonally averaged over the tomographic domain at all grid points along the meridional line EF (see Fig.1). Fig.7 shows the resulting temperature deviations along EF with the time plots for the 25-h mean temperature and diurnal, semidiurnal, and terdiurnal internal tides. In the figure, we can see that the water becomes increasingly warm. The range of 22℃ water increases from the northern coast to the central strait, and the 20℃ water in the central region gradually diminishes with time (Fig.7a). The temperature oscillation caused by the diurnal, semidiurnal, and terdiurnal internal tides are also clarified in Fig.7. Regarding the diurnal internal tides, the oscillation is regular in the central region and significantly strengthens along the northern coast with a delayed occurrence in the central region. The width of the northern coastal zones with strengthened oscillation is approximately 3 km. In contrast, the diurnal internal tides are less strengthened along the southern coast, forming an irregular pattern. The semidiurnal and terdiurnal internal tides generate a sporadic array of isolated cores in the central regions and weakly strengthen along the southern coast.

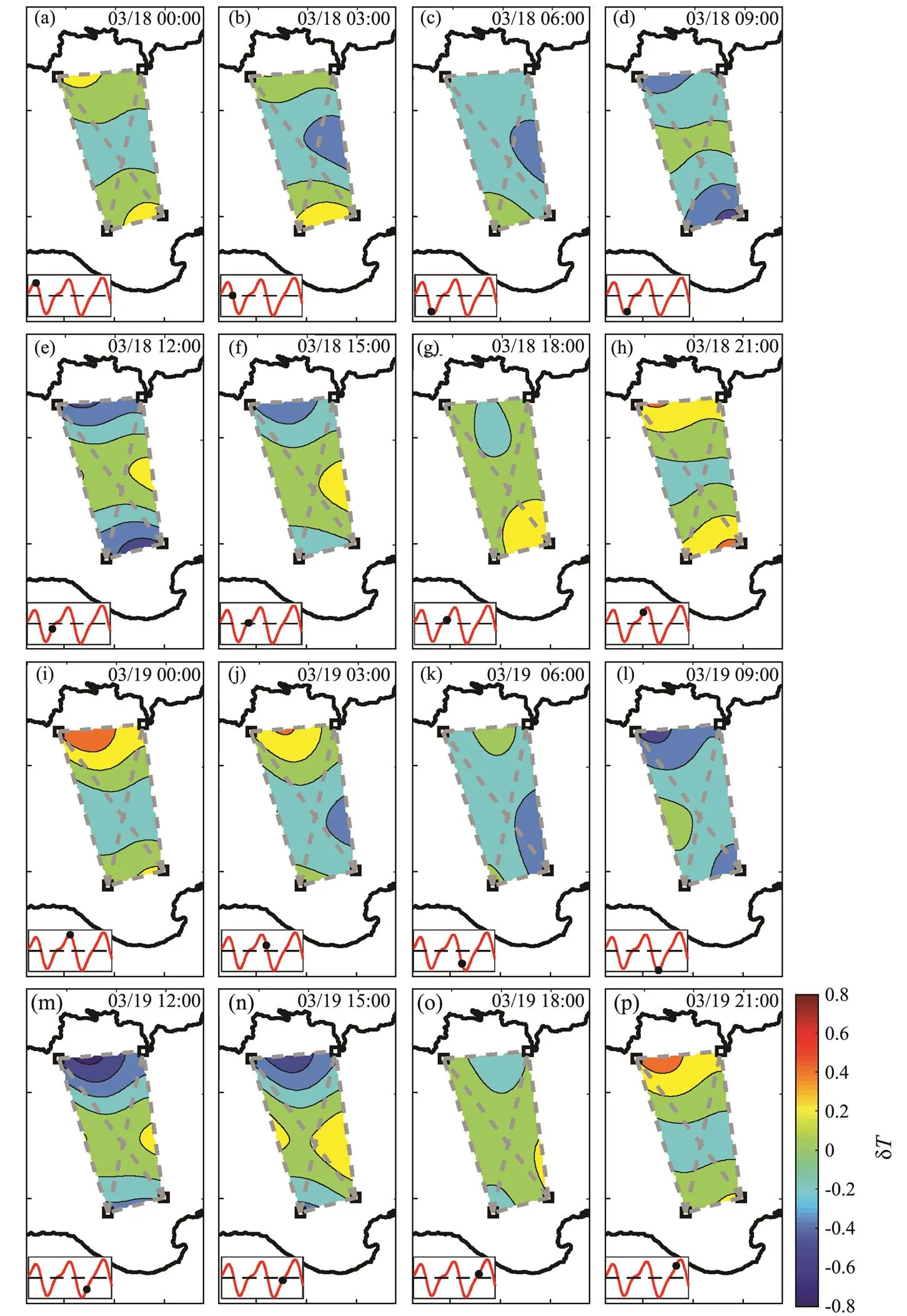
Fig.4 Three-hourly horizontal distribution of temperature (a–p) for the diurnal internal tide from March 18 to March 19. The observation times and the corresponding sea level heights (black dots) are indicated in the upper-right and lower-left corners, respectively.

Fig.5 Three-hourly horizontal temperature distributions (a–h) of the semidiurnal internal tide. The observation times and corresponding sea level heights (black dot) are indicated in the upper-right and lower-left corners, respectively.

Fig.6 Bihourly horizontal temperature distributions (a–i) of the terdiurnal internal tide. The observation times and corresponding sea level heights (black dot) are indicated in the upper-right and lower-left corners, respectively.

Fig.7 Meridional distributions and temporal variations of the 25-h mean and inverted temperature deviations along the EF: (a), 25-h mean temperature; (b), diurnal internal tide; (c), semidiurnal internal tide; and (d), terdiurnal internal tide. The dashed line in Fig.3b indicates the offshore boundary of the coastally trapped zone; the color bar on the right side of each figure indicates temperature.

4.3 Dynamic Modes

Dynamic mode analysis was performed on the CTD data, which was obtained in the center of the tomographic region. The vertical profiles and phase speeds of the dynamic modes, which can occur at the observation site, were determined from the analysis. Fig.8 shows the vertical velocity profiles for the first three dynamic modes, with the temperature, salinity, and density profiles. In the figure, we can see that the temperature decreases from 23.1℃ at the surface to 21.9℃ at 15m in depth and then remains constant from 15m to 70m. A thermocline is observed in the upper 10m. The salinity remains nearly constant from the surface to bottom. The depths of the maximum vertical velocity increase with the mode number,, 15m, 35m, and 38m for first, second, and third modes, respectively. The phase speeds are1=0.14ms−1,2=0.07ms−1, and3=0.05ms−1for the first, second, and third modes, respectively.

5 Discussion

The diurnal, semidiurnal, and terdiurnal internal tides in the Qiongzhou Strait were first presented based on direct observations, although numerical model results pre- dicted the intrusion of internal tides (Bai, 2015). In this study, dynamic mode analysis was performed to calculate the phase speed of these internal tides. The first internal mode of1=0.14ms−1may be a pronounced mode of the internal tides in this region, as it has been observed in various other seas (, Buijsman, 2014). If this first-mode identification is acceptable, the wavelengths are reduced to 12.1km, 6.3km, and 4.2km for the diurnal, semidiurnal, and terdiurnal internal tides, respectively, by multiplying1with the corresponding periods. This means that only the diurnal internal tide with a wavelength of 12.1km is well resolved by inversion with a spatial resolution of 4.4km (Figs.4, 5, and 6). Accurate measurement of the vertical profiles of the internal tides is required for more correct mode identification.

Fig.8 Vertical profiles of CTD data obtained on March 28 and vertical velocities of first, second, and third internal modes. (a) The red, black, and blue lines indicate density, temperature, and salinity, respectively. (b) The red, green, and black lines indicate the first, second, and third internal modes, respectively.

The diurnal internal tides generated at the shelf break east of Hainan Island may intrude into the Qiongzhou Strait from the east. The westward propagating internal tides are likely to be strengthened along the northern coast of the strait, where the Coriolis and pressure gradient terms in the momentum conservation equation are balanced within the scale of the Rossby internal radius of deformation (R); then, the coastally trapped effect is manifested in the zone with a width ofRalong the northern coast (Gill, 1982; Hsueh and Pang, 1989). The diurnal internal tide,1is represented by:

where1denotes the phase speed of the diurnal internal tide, and(=2Ωsin) denotes the Coriolis parameter. Ωanddenote the angular velocity of the Earth’s rotation and the latitude, respectively.1is reduced to 3km, which specifies the width of the coastally trapped zone confined along the northern coast (Fig.7b). In contrast, the coastally trapped zone generated along the southern coast by the eastward-propagating semidiurnal and terdiurnal internal tides are not resolvable as the wavelengths are equivalent to or smaller than the resolution of the inversion.

We note that the terdiurnal internal tides are generated by a nonlinear interaction between the semidiurnal and diurnal internal tides,,

Normally, M4tides dominate in coastal seas with strong semidiurnal tides (Zhu, 2017a). However, terdiurnal tides have replaced M4 tides in the Qiongzhou Strait where both diurnal and semidiurnal tides are pronounced.

The standard deviation (STD) of the mean travel times in a high-frequency band of 5min–1h was determined to be 0.0017s, which corresponds to a temperature STD of 0.12℃. This temperature error of 0.12℃ is significantly smaller than the amplitude of the diurnal internal tides (0.7℃), and the amplitudes of the semidiurnal and terdiurnal internal tides (0.4℃). The error estimation validated the accuracy of inverted results.

6 Conclusions

Three types of internal tides (diurnal, semidiurnal, and terdiurnal) were identified by the spectral analysis of RAT data and inverse analysis of mean travel time data obtained during the 2013 CAT experiment in the Qiongzhou Strait. For the northern transmission path, the diurnal spectrum was found to be significantly larger than the semidiurnal spectrum, but the semidiurnal energy was more pronounced along the southern transmission path than on the northern path. The energy of the terdiurnal internal tides was greater along the southern path than the northern path, and its spectrum was equivalent to the semidiurnal internal tides for both the northern and southern paths. These three types of internal tides were also distinguished by their two-dimensional distributions of the inverted temperature deviation. However, only the diurnal internal tides were re- solvablebecausetheirwavelength(12.1km)islongenough relative to the spatial resolution (4.4km) of the inversion.

The zonally averaged inverted temperature deviations over the tomographic domain showed that the diurnal internal tides were strengthened along the northern coast, which implies their westward propagation and the existence of coastally trapped effects due to the Earth’s rotation. The other two eastward-propagating internal tides were less strengthened along the southern coast due to the insufficient resolution of the inversion. We propose that the terdiurnal internal tides are generated by the nonlinear interaction between the semidiurnal and diurnal internal tides. The data quality was validated as satisfactory by error estimation using the STD of the mean travel times in a high-frequency band (5min–1h).

The source region of these internal tides is suspected to be located outside the tomographic region. In future work, a regional ocean model will be used to investigate the propagation of internal tides toward the Qiongzhou Strait from the northern South China Sea and Gulf of Beibu.

Acknowledgements

This study was supported by the National Natural Science Foundation of China (Nos. 41776107, 41920104006, 41906024,41906023,41806020,52071293,and41976001), the Scientific Research Fund of SIO (Nos. JB2004, JZ2001 and JT1801), and the Project of State Key Laboratory of Satellite Ocean Environment Dynamics, SIO (No. SOEDZZ2106).

Aruni, D. H., Fadli, S., Zhang, C., Mutsuda, H., Chen, M., Zhu, X. H.,, 2020. Tomographic measurement of tidal current and associated 3-h oscillation in Bali Strait., 236: 106655, https://doi.org/10.1016/j.ecss.2020.106655.

Bai, P., Li, P. L., Gu, Y. Z., and Wu, K. J., 2015. Interaction between upwelling and internal tide in the East Qiongzhou Strait areas., 1092: 1160-1164, DOI:10.4028/www.scientific.net/AMR.1092-1093.1160.

Buijsman, M. C., Klymak, J. M., Legg, S., Alford, M. H., Farmer, D., MacKinnon, J. A.,, 2014. Three-dimensional double-ridge internal tide resonance in Luzon Strait., 44: 850-869, https://doi.org/10.1175/JPO-D-13-024.1.

Chen, M., Kaneko, A., Lin, J., and Zhang, C., 2017. Mapping of a typhoon-driven coastal upwelling by assimilating coastal acoustic tomography data., 122: 7822-7837.

Duda, T. F., Lynch, J. F., Irish, J. D., Beardsley, R. C., Ramp, S. R., Chiu, C.-S.,, 2004. Internal tide and nonlinear internal wave behavior at the continental slope in the northern South China Sea., 29: 1105-1131, DOI: 10.1109/JOE.2004.836998.

Gill, A. E., 1982.. Academic Press, New York, 662pp.

Hsueh, Y., and Pang, I., 1989. Coastally trapped long waves in the Yellow Sea., 19 (5): 612-625.

Huang, H., Guo, Y., Wang, Z., Shen, Y., and Wei, Y., 2019. Water temperature observation by coastal acoustic tomography in artificial upwelling area., 19: 2655.

Kaneko, A., Yamaguchi, K., Yamamoto, T., Gohda, N., Zheng, H., Fadli, S.,, 2005. A coastal acoustic tomography experiment in Tokyo Bay., 24 (1): 86-94.

Kaneko, A., Zhu, X. H., and Lin, J., 2020.. Elsevier, Amsterdam, Netherlands, 347pp, https://doi.org/10.1016/B978-0-12-818507-0.00013-5.

Lin, J., Kaneko, A., Gohda, N., and Yamaguchi, K., 2005. Accurate imaging and prediction of Kanmon Strait tidal current structures by the coastal acoustic tomography data., 32: L14607, DOI: 10.1029/2005GL022914.

Mackenzie, K. V., 1981. Nine-term equation for sound speed in the ocean., 70807-812.

Munk, W., Worceser, P. F., and Wunsch, C., 1995.. Cambridge University Press, New York, 433pp.

Park, J-H., and Kaneko, A., 2000. Assimilation of coastal acoustic tomography data into a barotropic ocean model., 27: 3373-3376.

Sheng, J., and Wang, L., 2004. Numerical study of tidal circulation and nonlinear dynamics in Lunenburg Bay, Nova Scotia.,109: C10018, DOI: 10.1029/2004JC002404.

Shi, M. C., Chen, C. S., Xu, Q. C., Lin, H., Liu, G., Wang, H.,, 2002. The role of Qiongzhou Strait in the seasonal variation of the South China Sea circulation., 32 (1): 103-121.

Xu, Z., Yin, B., Hou, Y., Fan, Z., and Liu, A. K., 2010. A study of internal solitary waves observed on the continental shelf in the northwestern South China Sea., 29 (3): 18-25.

Yamaguchi, K., Lin, J., Kaneko, A., Yamamoto, T., Gohda, N., Nguyen, H.-Q.,, 2005. A continuous mapping of tidal current structures in the Kanmon Strait., 61 (2): 283-294.

Yamaoka, H., Kaneko, A., Park, J.-H., Zheng, H., Gohda, N., Takano, T.,, 2002. Coastal acoustic tomography system and its field application., 27 (2): 283-295.

Zhang, C., Kaneko, A., Zhu, X. H., and Gohda, N., 2015. Tomographic mapping of a coastal upwelling and the associated diurnal internal tides in Hiroshima Bay, Japan., 120 (6): 4288-4305, DOI: 10.1002/2014JC010676.

Zhang, C., Zhu, X. H., Zhu, Z. N., Liu, W., Zhang, Z. Z., Fan, X. P.,, 2017. High-precision measurement of tidal current structuresusingcoastalacoustictomography., 193: 12-24.

Zhao, R., Zhu, X. H., Park, J. H., and Li, Q., 2018. Internal tides in the northwestern South China Sea observed by pressure-recording inverted echo sounders., 168: 112-122, https://doi.org/10.1016/j.pocean.2018.09.019.

Zhu, X. H., Kaneko, A., Wu, Q., Zhang, C., Taniguchi, N., and Gohda, N., 2013. Mapping tidal current structures in Zhitouyang Bay, China, using coastal acoustic tomography., 38 (2): 285-296.

Zhu, X. H., Ma, Y. L., Guo, X. Y., Fan, X., Long, Y., Yuan, Y. C.,, 2014. Tidal and residual currents in the Qiongzhou Strait estimated from shipboard ADCP data using a modified tidal harmonic analysis method., 119 (11): 8039-8060, DOI: 10.1002/2014JC009855.

Zhu, X. H., Zhu, Z. N., Guo, X., Ma, Y. L., Fan, X., Dong, M. H.,, 2015. Measurement of tidal and residual currents and volume transport through the Qiongzhou Strait using coastal acoustic tomography., 108: 65-75.

Zhu, Z. N., Zhu, X. H., and Guo, X., 2017a. Coastal tomographic mapping of nonlinear tidal currents and residual currents.,143: 219-227, https://doi.org/10.1016/j.csr.2016.06.014.

Zhu, Z. N., Zhu, X. H., Guo, X., Fan, X., and Zhang, C., 2017b. Assimilation of coastal acoustic tomography data using an unstructured triangular grid ocean model for water with complex coastlines and islands., 122: 7013-7030, DOI: 10.1002/2017JC012715.

. E-mail: xhzhu@sio.org.cn

May 12, 2020;

August 1, 2020;

December 29, 2020

© Ocean University of China, Science Press and Springer-Verlag GmbH Germany 2021

(Edited by Xie Jun)