基于PSO-SVR-LSTM水位预测模型研究
顾乾晖,胡 翌,涂振宇
(1.南昌工程学院 信息工程学院,江西 南昌,330099;2.江西省赣抚平原水利工程管理局,江西 南昌,330096)
0 引言
水位预测的精确性对于防汛抗旱、航道管理和水资源调度与利用有着重大意义。河流水位具有复杂性、季节性、波动性等特点[1]。并且受到降水量、支流和气候变化等多种因素的影响,特别是近年来的异常气候,这使得对河流水位预测变得更加复杂、更加困难。
近些年,随着人工智能和大数据的快速发展,越来越多的学者利用机器学习和深度学习对水位进行预测。许国艳和朱进[2]等人利用CNN和MC组合模型对水位进行预测,并与其他模型进行对比,实验结果表明取得良好的效果。郭燕和赖军[3]把支流作为影响因子输入LSTM神经网络预测鄱阳湖水位,取得不错的精度。商其亚和程耀东[4]等人利用混沌粒子群优化SVM参数,以此来对水位进行预测。要震[5]等人利用遗传算法优化Elman模型对水位进行预测,实验结果表明精确度得到了提高。
在实际环境下,影响河流水位的因素众多,河流水文数据不仅呈现出非线性特征也有时序性、复杂性和波动性特征[6]。SVR虽然在捕捉非线性数据上表现出强大的能力,但无法考虑时序变化。同时影响水位数据因素众多并且水文数据中包含许多复杂和不确定信息,运用单一模型往往预测效果不理想。而LSTM神经网络不仅能处理多元变量之间的非线性映射关系,也能很好的处理时间序列数据[7]。
因此,为了更好的提高预测效果,本文首先利用PSO分别对SVR和LSTM这两种模型进行寻优,之后将优化后的SVR和LSTM这两种模型进行按比例组合。本文提出的模型既可以处理水位变化的非线性特征,也能同时考虑水位变化的时序性和复杂性。利用该组合模型去预测修河水系的万家埠逐日水位量变化,取得很好的预测效果。
2 基于PSO-SVR-LSTM水位预测模型
2.1 LSTM神经网络概述
LSTM神经网络是从RNN神经网络基础上改进而来,LSTM神经网络中的门控单元(输入门、输出门、遗忘门)使得模型具有较长时间的“记忆功能”,因此LSTM神经网络适用于长时间非线性序列预测问题,LSTM神经网络的结构图如图1所示。
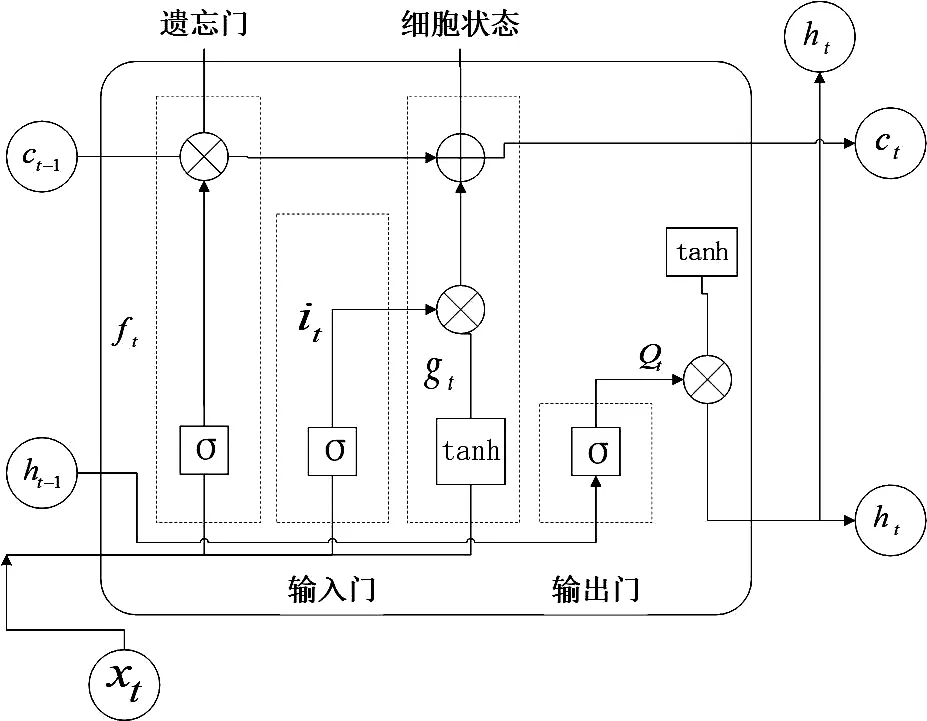
图1 LSTM基本单元结构
模型的输入数据分别为t时刻的输入数据xt,t-1时刻的记忆值ct-1和t-1时刻的LSTM的输出值ht-1,输出数据分别为t时刻的记忆值ct和LSTM输出值ht。
“遗忘门”通过ft保留和丢弃上一时刻的记忆单元ct-1的信息来影响当前时刻的细胞状态[8]。ft公式如下:
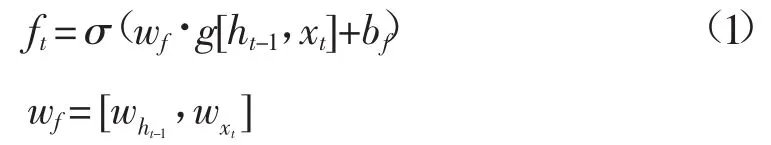
式中,σ为 sigmoid激活函数;bf为偏置顶;wht-1为输入数据ht-1对应的权重;wxt为输入数据xt对应的权重。
“输入门”通过激活函数sigmoid将变量控制在[0,1]之间,并输出 it。公式如下:
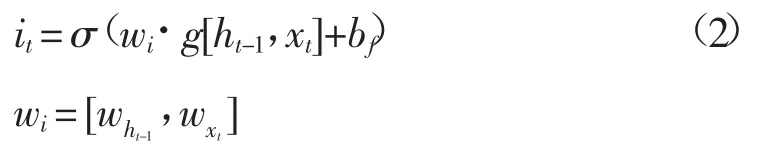
“遗忘门”和“输入门”的变化决定了细胞状态ct的变化。公式如下:
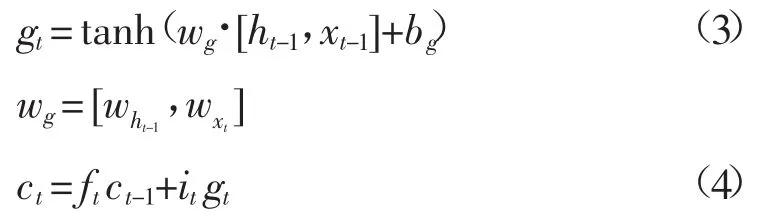
式中,bg为偏置顶;其余符号意义同前。
“输出门”用来控制当时时刻细胞状态值的输出。公式如下:
2.2 SVR概述
SVR(支持向量回归机)是Vapnik等人[9]在1995年提出的一种以统计学理论为基础的回归预测算法。SVR以结构风险最小化的核心思想,通过构建非线性映射,将原始数据集从低维空间映射到更高维的特征空间,然后在高维空间中通过创建一个线性函数得到预测值,改线性函数公式为:

式中:φ(x)为原始数据映射到高维空间的映射函数;w为权值向量;b为偏置顶。
在SVR训练过程中可以将建模问题转换为二次凸规划问题,其形式如下:
式中:c为惩罚项系数;ξi,ξ^i为松弛变量;ε 为不敏感损失函数。通过引入拉格朗日乘子算法将约束条件融入到公式(8)中,最终得到SVR模型如下所示:
式中:a 为大于 0 的拉格朗日乘子;K(x,xi)为满足Mercer条件的核函数。
2.3 PSO-SVR-LSTM组合模型
2.3.1 粒子群(PSO)优化SVR和LSTM
SVR模型的预测效果受到惩罚系数c以及核参数g取值的影响,因此c和g的选择对SVR模型的性能有着重大影响[10]。LSTM神经网络虽然在处理长时间序列数据上有着很好的效果,但是LSTM计算过于复杂,并且当输入越长,数据间包含的信息量就越大,传统的LSTM模型在训练过程中会表现出明显的不稳定性,甚至会出现梯度消失的现象[11]。
粒子群优化算法(PSO)是一种群智能优化算法。粒子群的优化是将种群中的个体当成多维搜索空间的粒子,每个粒子都有一个由目标函数决定的适应度值,在每一次迭代中,每一个粒子通过寻找个体最优位置和全局最优位置来不断更新自己的位置和速度,直至到达寻优条件[12]。
因此本文通过粒子群优化(PSO)算法自动迭代寻优LSTM模型两个重要参数:神经元个数(m)和学习率(lr)以及SVR模型的两个重要参数惩罚系数c以及核参数g,并把水位预测结果的均方误差(MSE)作为目标函数,MSE公式如下所示:
式中:yt是真实数据,pt是预测值。
2.3.2 SVR-LSTM模型组合
多变量时序单元的输入即LSTM神经网络的输入,把前7天的日均水位、日均水流量、日降水量值作为LSTM模型的输入,后1天的水位值作为输出。输入数据表达式见公式(11)。
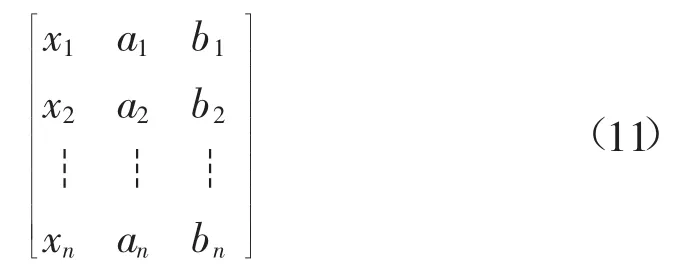
式中:x、a、b分别表示日均水位、日均水流量、日降水量数据。
非线性单元的输入即SVR模型的输入,把前7天的水位值作为SVR模型的输入,后1天的水位值作为输出。输入数据表达式见公式(12)。

式中:x表示水位数据。
2.3.3 PSO优化SVR-LSTM组合模型
通过PSO优化SVR-LSTM组合模型,得到PSOSVR-LSTM组合模型的输出值为PSO-LSTM时序单元的预测值和PSO-SVR非线性单元的预测值的比例组合,组合模型的表达式如下:

式中,XT表示1日水位预测值;LT表示PSO-LSTM时序性单元输出的1日水位预测值;ST表示PSO-SVR非线性单元输出的1日水位预测值;a表示为(0,1)之间的数值。图2为PSO-SVR-LSTM组合模型结构图。
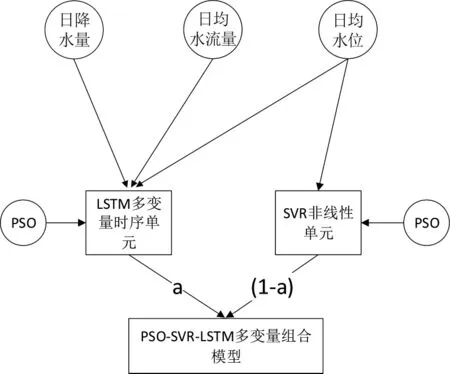
图2 PSO-SVR-LSTM组合模结构图
2.4 整体流程
组合预测模型流程图如图3所示,其具体步骤如下。
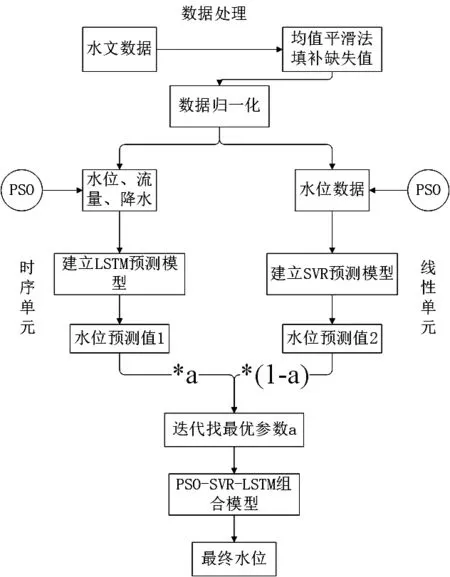
图3 PSO-SVR-LSTM组合模型流程图
Step1:为了降低数据的波动性,对日均水位、日降水量和日均水流量这三组数据进行最大最小值归一化。
Step2:构建LSTM神经网络时序水位预测单元。把日均水位、日降水量、日均水流量这三组数据作为LSTM模型的输入,在LSTM模型中进行训练,同时把LSTM模型预测到的水位数据作为该模型的输出。
Step3:构建SVR非线性水位预测单元。把水位这个单独变量作为SVR模型的输入,同时把SVR模型预测到的水位数据作为该模型的输出。
Step4:利用粒子群(PSO)分别优化SVR和LSTM模型参数,选取均方误差MSE作为评价标准和各粒子的适应度值,得到两组模型的最优参数。
Step5:令经过PSO优化后的LSTM模型的权重值为a。同时令经过PSO优化后的SVR模型的权重值为(1-a)。分别利用各自的权重值组合成水位组合预测模型,其表达式具体见公式(13)。
Step6:通过不断迭代寻找最优的权值参数a,并利用组合模型对水位进行预测,得到最终水位预测值。
3 仿真分析
3.1 实验平台与环境
实验所使用计算机配置如下:处理器为(英特尔)Intel(R) Core(TM) i5-8400 CPU@2.80GHz,显卡为NVIDIA GeForce GTX 1050 Ti,内存为 16 GB,操作系统为windows10;程序设计语言为Python3.7;集成开发环境为Anaconda和Visual Code;程序中TensorFlow由2.1.0版本实现,scikit-learn由0.2.0版本实现。
3.2 数据选择
本文所用的数据是江西南昌潦水水域万家埠水文站,选择从2017年1月1号至2020年12月30号的逐日平均水位、日均流量、日降水量数据,共1462条数据,其中日降水量为整个潦水流域的日降水量的算术平均值。将前三年数据作为训练集,后一年数据作为测试集。训练集与测试集按比例分别划分为80%与20%,数据集划分如图4所示。
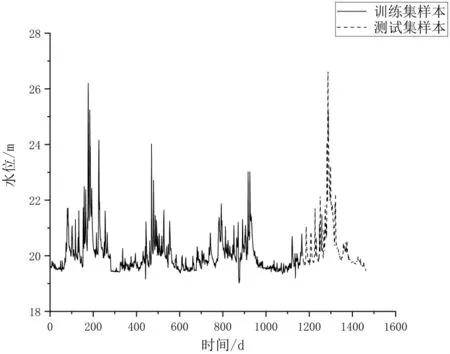
图4 万家埠水位数据集
3.3 数据预处理
由于水文数据类型不同,为了提高模型的收敛速度和计算精度,需要对样本数据进行最大最小值归一化处理,即:

式中,ximax表示变量i的最大值;ximin表示变量i的最小值。
3.4 网络模型参数选择与实验结果
将收集到的在线水文数据经过数据归一化后作为PSO-SVR-LSTM组合模型的输入参数,并利用均方误差MSE作为评价指标。
为了验证本文提出的预测模型的有效性,选取BP、SVR、PSO-SVR、PSO-LSTM 和 PSO-BP-LSTM 等预测模型与PSO-SVR-LSTM模型进行对比实验。这几种预测模型均在相同的实验平台和环境下进行实验。
首先利用粒子群算法(PSO)分别对LSTM神经网络的神经元个数m1、学习率lr和拥有rbf核函数SVR的惩罚因子c、核参数g以及单隐含层的BP神经网络的神经元个数m2进行寻优,将MSE作为目标函数,最后优化后的各个模型的参数取值见表1。
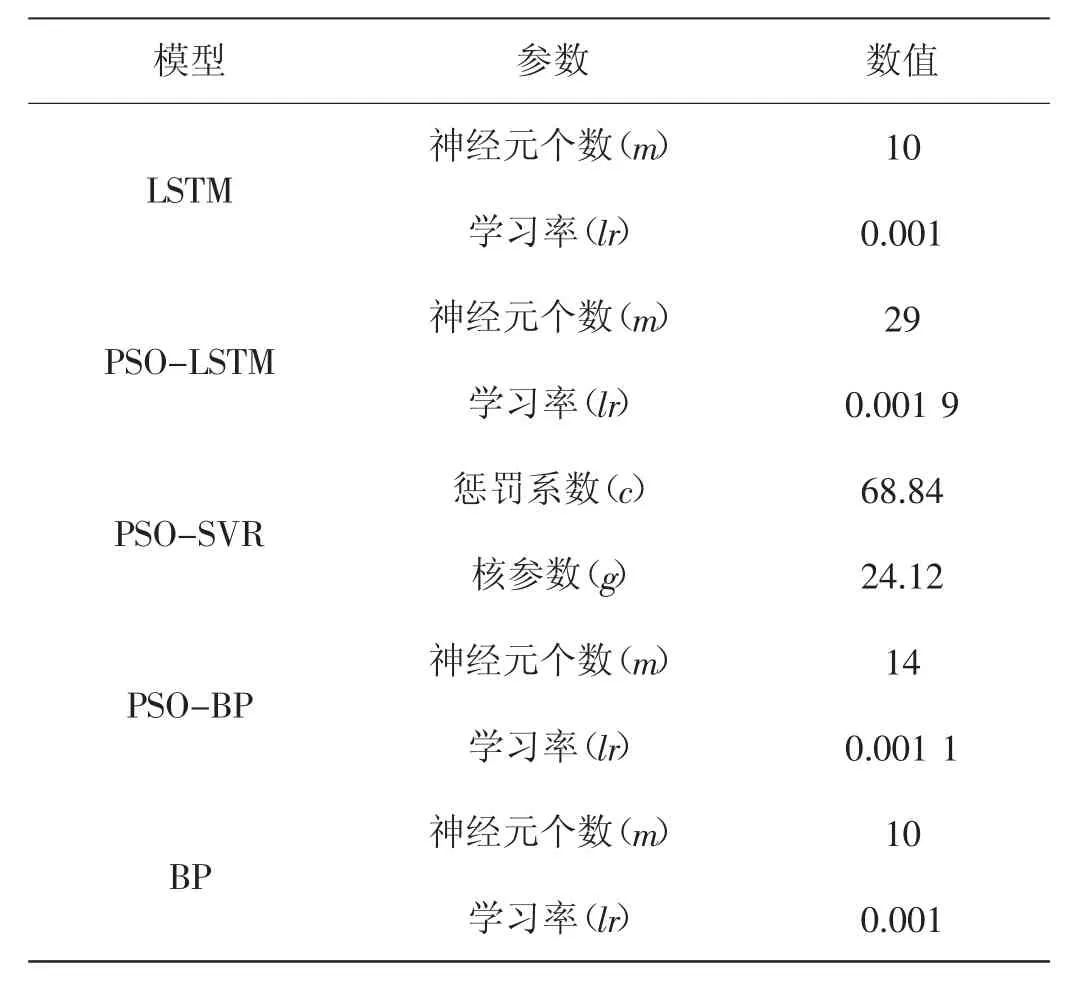
表1 对比模型参数设置
接着对于PSO-SVR-LSTM组合模型,利用不断迭代寻找组合的模型的最优权重a。最终经过PSO寻优后,得出权重值a为0.82。
为了更加直观的看出本文提出的PSO-SVR-LSTM模型在预测精度上的提高,分别对各个模型进行绘图。如图5和图6所示,经过PSO优化后的LSTM和BP模型都要比普通LSTM和BP的准确度效果要好。如图7所示,虽然PSO-SVR模型与水位真实数据偏离度较高,但是相对于其他模型,PSO-SVR在波峰点以及线型上与真实数据更相似。如图8所示PSO-SVR-LSTM模型在精确度以及拟合度上都要比PSO-LSTM和PSOSVR效果好。
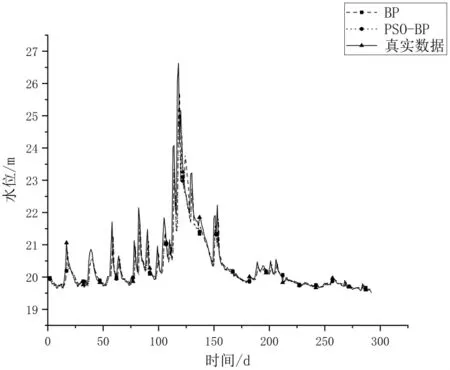
图5 BP与PSO-BP模型预测值
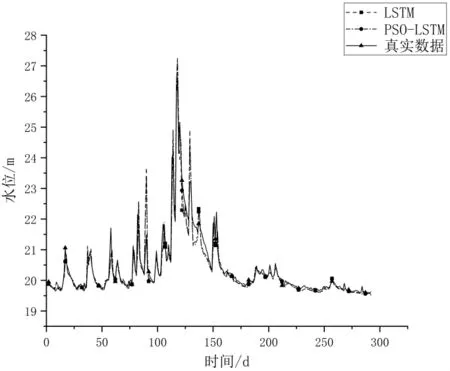
图6 LSTM、PSO-LSTM预测值
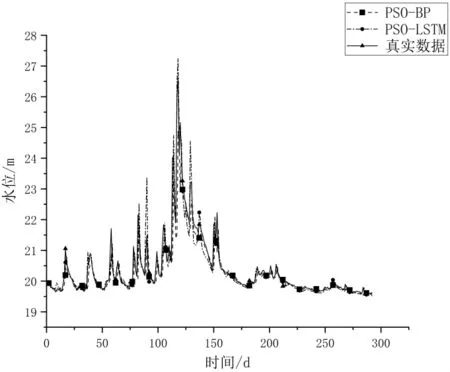
图7 PSO-BP、PSO-LSTM预测值
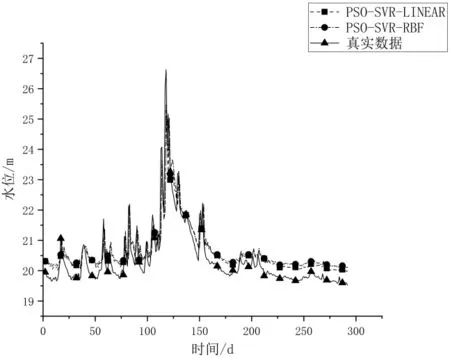
图8 PSO-SVR-LINEAR与PSO-SVR-RBF预测值
为了更加精确体现各种模型之间的性能对比,根据真实数据与预测数据绘制出这四种模型的性能对比表,如表2。可以从表中看出,PSO-SVR-LSTM组合模型在MSE、MAE、R2以及RMSE四种评价指标上都比其他模型效果要好。
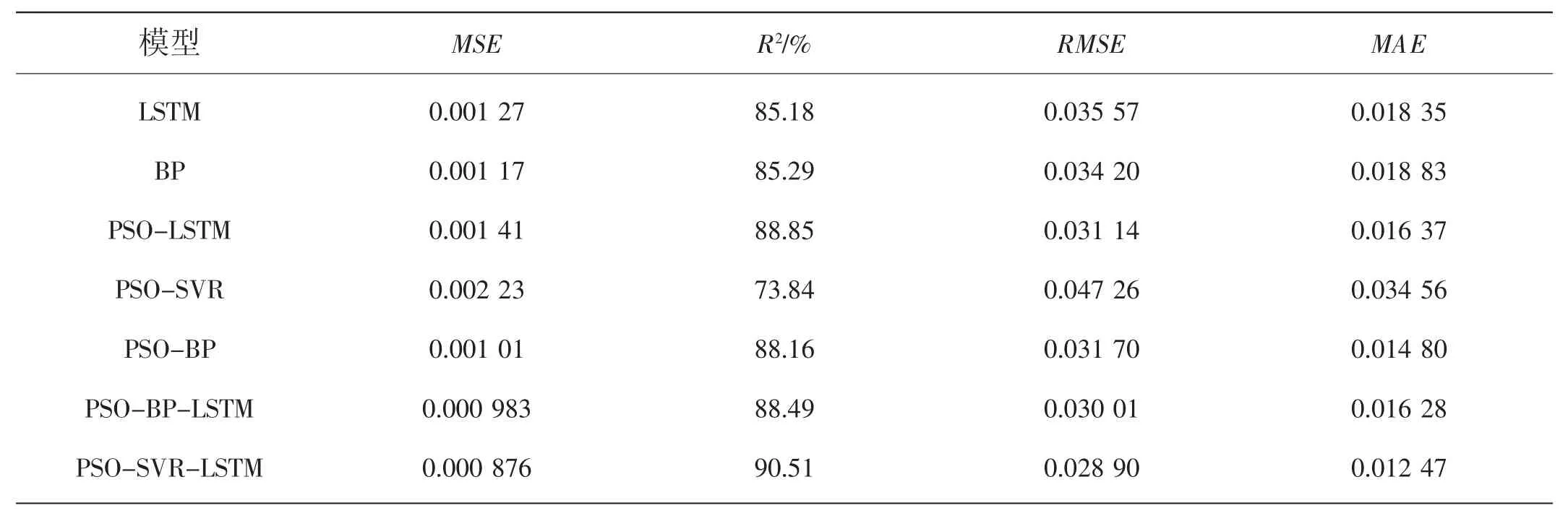
表2 模型性能对比表
从以上实验结果可知,本文提出的PSO-SVRLSTM组合模型预测模型均方误差(MSE)和平均绝对误差(MAE)最小,决定系数(R2)最大。相对于其他水位模型,PSO-SVR-LSTM组合模型有着较强的泛化能力和预测精度。因此本文提出的PSO-SVR-LSTM模型可以有效运用于河流的水位预测当中。
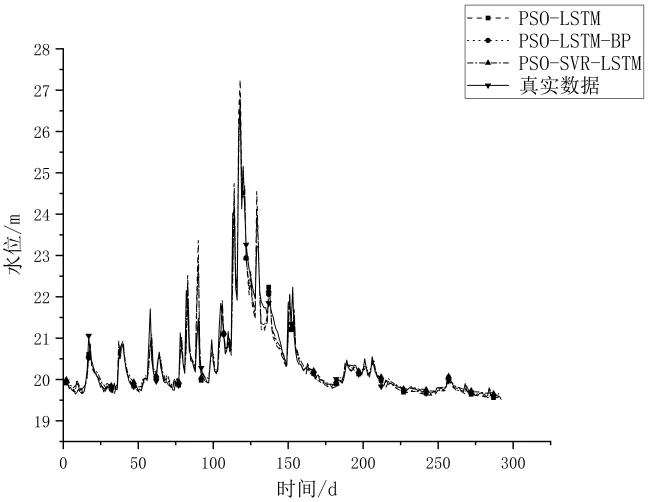
图9 PSO-LSTM-BP、PSO-LSTM、PSO-SVR-LSTM 预测值
4 结论
本文首先将河流日均水位、日降水量、日均水流量数据通过均值平滑法填补缺失值。为了减少数据的波动,通过最大最小值归一化方法对数据进行处理。然后把处理后水位数据放入SVR非线性单元中,把日均水位、日降水量、日均水流量数据放入LSTM单元中。通过粒子群(PSO)分别优化SVR和LSTM,再通过迭代找出最优权值a。实验结果表明本文提出的PSO-SVRLSTM预测模型的误差最小,与真实数据更加吻合,预测模型的性能比 PSO-LSTM、PSO-SVR、PSO-BP和PSO-BP-LSTM等预测模型更加准确、取得更好的预测效果,为水位预报决策和防洪抗旱提供更有力的参考依据。

