部分框支剪力墙结构转换构件及上部剪力墙分析

朱德胜

（重庆建普城市建设发展集团有限公司，重庆400014）

0 引言

现代高层建筑中，由于底部要求设置大空间，上部框架柱或剪力墙不能直接连续贯通落地，需设置转换层，在结构转换层布置转换结构构件。主要结构转换方式有：梁式转换、桁架转换、厚板转换等。梁式转换具有传力途径明确直接、受力性能好、构造相对简单、施工方便、结构设计相对容易等优点，被广泛应用[1]。本文主要分析梁式转换结构的转换梁及上部剪力墙在竖向荷载作用下的内力、应力和变形，以及不同分析模型对分析结构的影响对比。

转换构件由于承受上部多层柱或剪力墙传递的竖向、水平向荷载以及底部弯矩，转换构件受力较大且较为复杂。水平转换构件的竖向刚度（在竖向荷载作用下的变形）对上部被转换的墙柱内力影响较大，过大的变形将导致上部竖向构件内力突变严重，使得上部被转换竖向构件处于多向的复杂应力状态，影响构件的抗震性能[2]。设置转换层，结构沿竖向刚度发生突变，荷载传递途径发生变化，荷载作用下转换构件的内力集中，故转换结构设计将重点关注转换构件和其上部竖向构件的受力。

在做转换层结构设计时，经常会遇到转换层上一层的剪力墙墙肢轴力、水平“剪力”、弯矩很大甚至部分构件超限的问题，而转换层以上二层墙肢内力又正常。本文采用midas Gen通用有限元软件，以梁单元、板（壳）单元和实体单元模拟转换梁，通过力学分析转换梁及上部剪力墙的受力状态，分析产生这种现象的原因。

1 分析模型

为探究转换梁及上部剪力墙的力学现象及受力本质，采用一简单规则的框架剪力墙结构，在一层通过转换梁转换上部剪力墙，采用不同的力学假定分析对比不同模型的内力情况。

采用12层框架剪力墙结构模型，平面尺寸采用对称的2跨9m×9m，转换梁尺寸400mm×1000mm，剪力墙厚度250mm，地震烈度7度（0.10g），场地II类，场地特征周期Tg=0.35s，阻尼比0.05，基本风压0.4kN/m2，具体模型如图1所示。

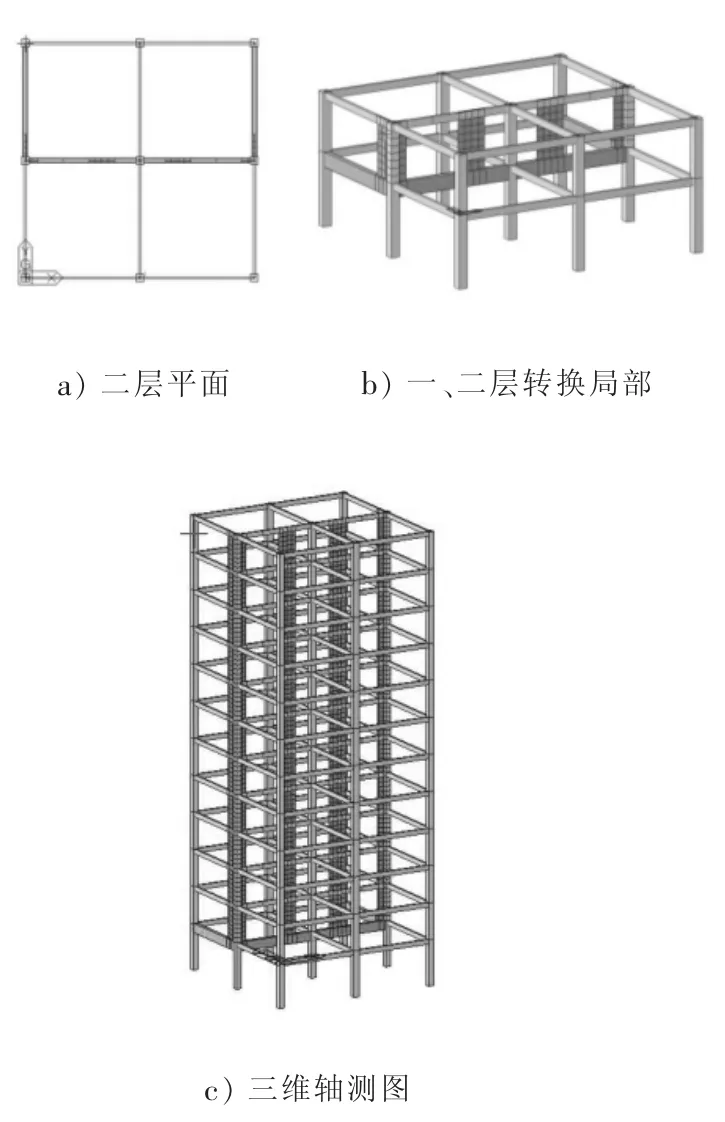
图1 模型基本情况

转换梁计算模型假定：模型一采用梁单元；模型二采用板单元；模型三采用实体单元。二层不考虑刚性楼板，为了更清晰了解转换梁受力情况，也不考虑二层转换层板厚，只考虑楼板导荷。转换层上部剪力墙采用板单元模拟，midas Gen板单元能真实模拟墙面内、外刚度，可以进行水平和竖向有限元划分，方便分析应力分布，真实反映墙体实际受力。

2 整体计算指标对比

2.1 周期对比

不同模型周期对比如表1所示。

表1 不同模型周期对比

2.2 层间位移角对比

各模型层间位移角如表2、表3、表4所示（仅列出下部5层数据，经分析其余楼层规律基本相同）。

表2 模型一层间位移角

表3 模型二层间位移角

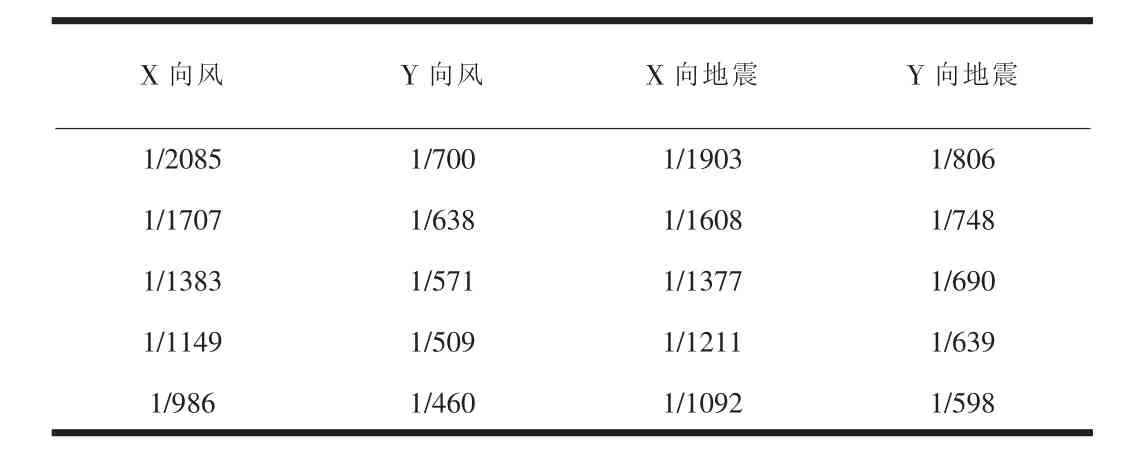
表4 模型三层间位移角

通过以上三个模型周期、层间位移角对比，不同的转换梁模型假定计算的整体指标基本相同，误差较小，故结构构件所分配的外力也基本相同，局部对比分析具有可行性。由于本次分析的重点是转换梁及其上部剪力墙在竖向荷载作用下的力学现象和应力分布规律，采用模型较为简单，实际工程中不同模型计算数据误差可能会大于该模型。

3 转换梁计算内力对比分析

选取中部转换梁进行分析，由于此转换梁分别在支座和跨中有承托的剪力墙，受力更具有典型性。具体转换梁位置如图2所示。

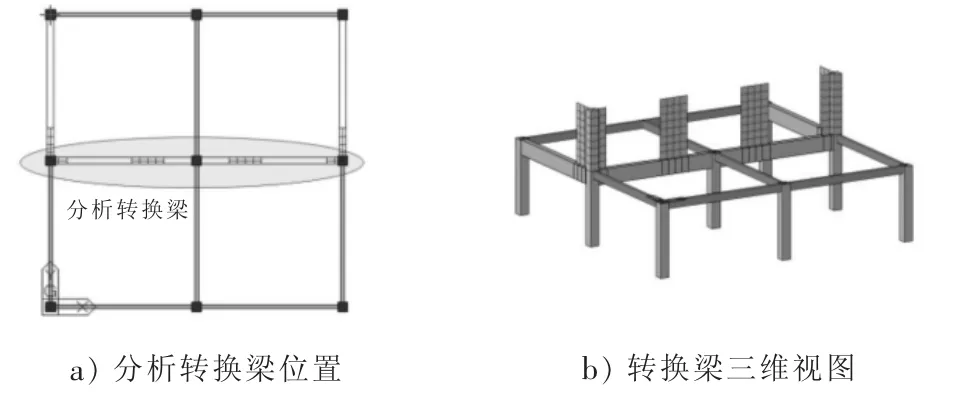
图2 选取转换梁位置

3.1 不同模型转换梁内力对比分析

软件只能显示梁单元的内力计算结果，板单元和实体单元不能直接输出内力结果，只能通过应力积分得到内力值[3]。板单元和实体单元模拟转换梁在与上部剪力墙端交接处均出现局部应力集中，若以此处截面积分得到内力，会产生局部内力突变。为了能更真实反映不同模型真实受力情况，分别选取应力变化相对均匀的截面进行对比，如图3截面1、截面2、截面3、截面4。对比结果如表5所示。

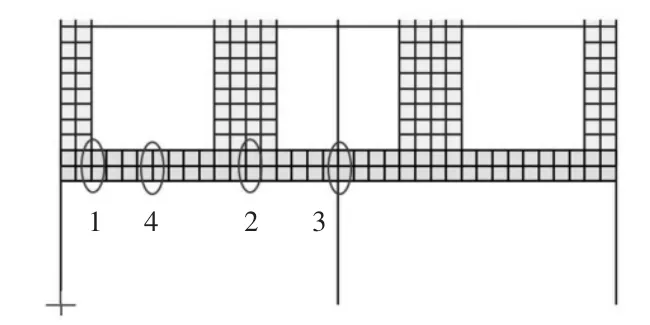
图3 对比选取截面位置

表5 工况（1.2恒+1.4活）单位（kN·m）

通过以上数据，发现板单元和实体单元模拟转换梁计算结果较为接近，和梁单元计算结果相比，没有特定规律，主要由被转换剪力墙作用位置、转换梁截面尺寸及抗弯刚度等因素决定，剪力墙作用范围外转换梁段及4截面计算结果比较接近。

3.2 不同单元模拟计算结果出现差异的原因

（1）单元自由度和边界条件的差异。板单元每个节点具有x、y、z轴方向的移动的线性位移自由度和绕x、y轴旋转的旋转位移自由度，及板单元节点无平面内旋转自由度[4]，故在板单元节点与两端柱连接处只传递拉压力，类似桁架单元连接，节点内力精度与有限元划分数量及连接节点数量有关，连接节点越多精度越高。

（2）不同单元模拟转换梁对截面尺寸的假定。有限元软件梁单元截面尺寸仅提供轴向和抗弯刚度，及简化为被赋予梁截面特性的位于中性轴的线单元，转换梁上部的剪力墙实际与梁中性轴相连接，忽略了梁的尺寸效应，在支座节点仅能保证与梁柱的中性轴转角位移相协调，梁顶和梁底节点与之相邻的柱实际转角位移是不协调的。转换梁顶面与剪力墙底端节点实际位移也是不协调的，故梁单元模拟转换梁计算结果有一定近似性。板单元和实体单元模拟的转换梁顶与上部剪力墙按实际连接，可以做到接触面的变形协调，计算结果更合理。

以上三种模型计算结果转换梁均出现较大轴力，且同一跨梁被上部剪力墙节点分割后出现拉力和压力，受力类似于桁架下弦杆，剪力墙类似于腹杆。在框支剪力墙结构设计分析计算时，转换层楼板应按弹性板考虑，这样才能真实计算出转换梁轴力，转换梁按拉弯或压弯构件考虑，若按刚性楼板考虑，楼板平面内节点刚性约束于楼板形心处，面内无变形，不能真实反映转换梁及其上部剪力墙的受力情况。由于转换梁受力复杂且重要，转换层楼板构造厚度较大，在实际设计时为提高转换梁安全储备，软件在模型假定时可能导致计算结果不确定，可以偏安全地不考虑楼板的影响，所有轴向力由转换梁承担。《高规》10.2.7也规定转换梁应加强梁上部通长筋和两侧腰筋[5]。

由于不同单元假定计算结果有一定差异，在剪力墙与下部转换梁连接处内力突变严重，《高规》5.1.15条文中明确说明，对转换构件等受力复杂部位应按应力分析结果进行截面配筋设计校核。

4 转换梁上部剪力墙变形、应力分析

在转换层结构分析时，经常遇到转换梁上一层墙体内力突变（轴力、“剪力”、弯矩），配筋异常大甚至截面超限，上部楼层却受力合理的现象。可从转换梁及其上部墙体的应力分布和变形分析其原因。

由于梁单元不能进行有限元剖分，不能得出应力分布情况。板单元能真实模拟面内面外刚度，剖分后可以得出应力分布规律。转换梁和上部剪力墙均采用板单元[6]，能够真正做到节点变形协调、分析结构可靠。

4.1 竖向荷载作用转换梁和上部剪力墙竖向变形

竖向荷载作用下，转换梁产生竖向变形，由于梁上各点变形差异导致上部剪力墙发生弯曲变形（图4）。

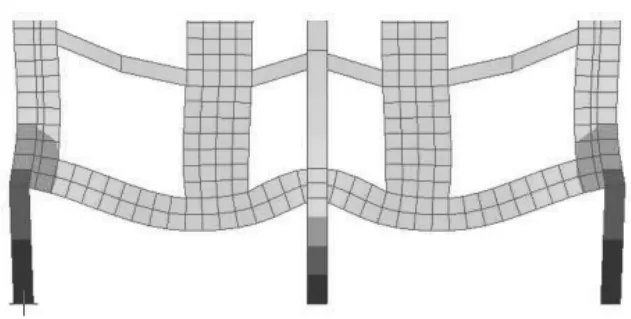
图4 1.0恒+1.0活作用下竖向变形

4.2 竖向荷载作用下剪力墙应力分布

截取转换梁及上部剪力墙在竖向荷载作用下的应力分布，如图5所示。

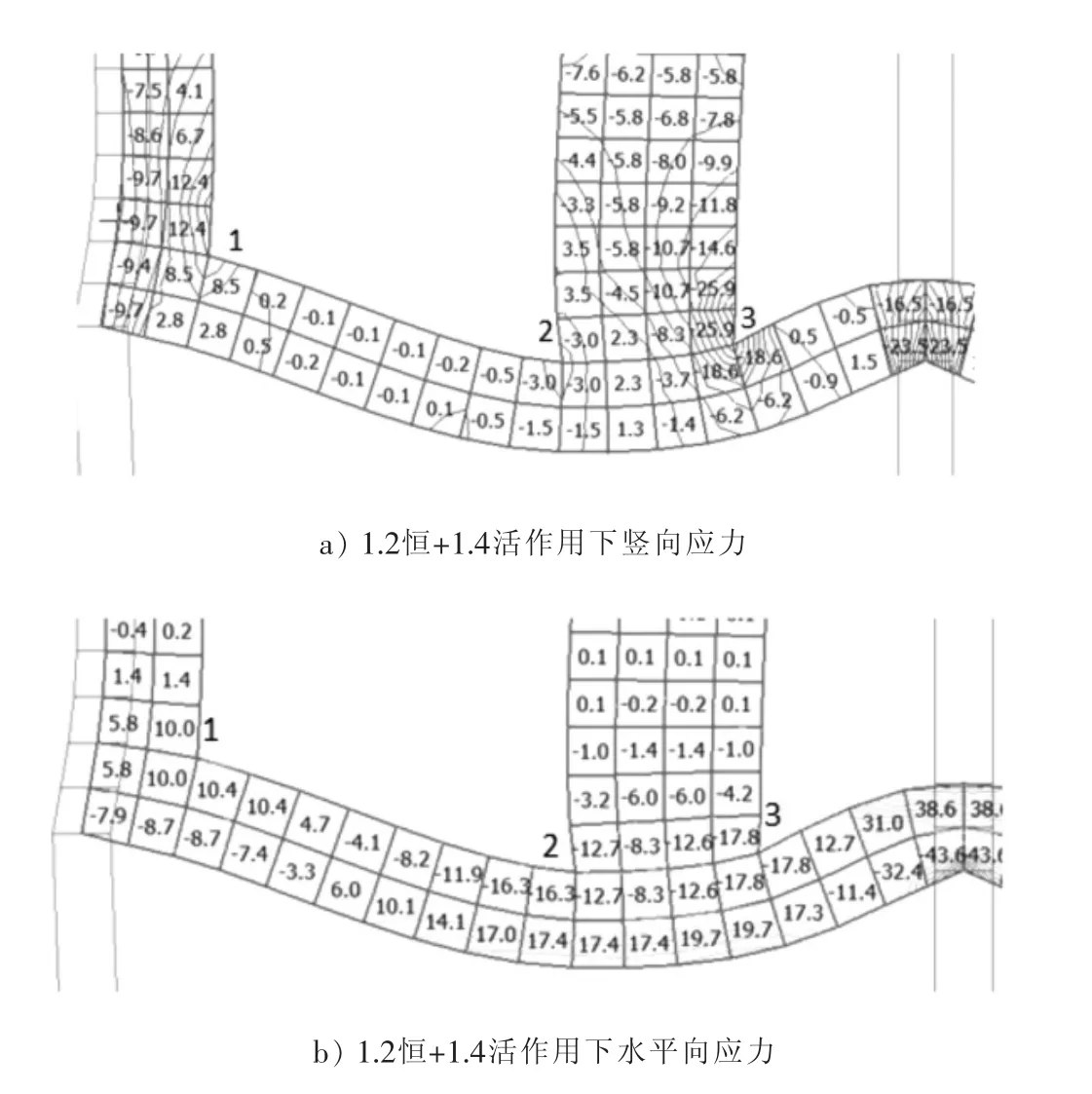
图5 1.2恒+1.4活荷载作用下应力分布

剪力墙端部与转换梁连接处均出现较大应力突变，其中1位置处剪力墙在竖向荷载下出现较大拉压力，主要由于转换梁向下变形导致局部剪力墙受拉，3位置转换梁转角位移较大，导致上部剪力墙单元发生较大变形，应力突变明显，相应转换梁单元也发生较大局部压应力。这就能很好解释转换层上部剪力墙轴力突变轴压比超限现象。

在竖向荷载作用下，转换层上部剪力墙由于水平向受到转换梁约束，最左侧墙肢的左端节点位于柱截面范围内，竖向变形较小，在1位置处右端节点位于跨中产生竖向变形，从而导致水平向出现较大拉压力[6]，这就解释了支座处转换的剪力墙为何有时会出现“剪力”超限问题，墙肢越长越明显，此“剪力”并非由水平向荷载作用产生，而是由竖向荷载作用下两端产生变形差导致墙体受拉。2、3位置位于转换梁跨中，竖向荷载作用下产生明显的挤压变形，水平向出现较大压应力，特别在3位置处，单元受到较大竖向压应力和水平向压应力，最大主应力将发生在斜截面上，σ1∶最大的主应力=，若此时剪力墙轴压比仅按竖向荷载作用计算，斜截面实际主压应力大于竖向压应力值，从而导致斜面上的轴压比超过规范值[7]，剪力墙在地震作用下延性降低，存在一定安全隐患。一般规律是转换梁负弯矩区梁顶面受拉，相应剪力墙受到水平拉力，正弯矩区梁面受压，上部剪力墙水平受压，也可理解为转换梁应力扩散至上抬剪力墙。

对于转换梁上部剪力墙应力突变，可以通过转换和不转换两种方式进行对比。在竖向荷载作用下（1.2恒+1.4活）墙体应力、内力如图6所示。

图6 转换和不转换墙体应力对比

转换与非转换剪力墙底端截面内力对比如表6所示。

表6 墙体落地与墙体转换内力对比

通过对以上两种模型剪力墙体应力分布和内力提取可知，转换层上部剪力墙局部应力集中，从而导致内力突变。根据前文所述，应力突变的原因是，转换梁的竖向变形使上部剪力墙两端变形不一致，导致平面内整体弯曲。提高转换梁抗弯刚度可缓解应力突变，但不能根本消除。

因为转换梁上部墙体的内力突变是由竖向荷载引起的，故在设计时不能忽视此影响，应通过有限元计算，按应力配筋，对于出现水平拉应力较大的墙体，应配置水平钢筋承担此拉应力。对于出现水平压应力较大的墙体，由于墙体处于竖向和水平向双向应力状态，最大主应力出现在斜截面上，故应按斜截面上正应力验算剪力墙轴压比。建议不要在转换层上部的墙体内开洞，若不能避免，应按剪力墙开洞的模型验算剪力墙以及下部的转换梁应力，转换梁上部墙体除计算要求外构造加厚。

5 结论

（1）用梁单元、板单元和实体单元计算框支剪力墙结构整体指标时，结果基本一致。

（2）转换梁用梁单元、板单元和实体单元模拟计算时，结果有一定差异，特别在上部剪力墙与转换梁接触处差异更大，这主要由于不同计算单元模型假定以及边界条件不同，故转换梁配筋采用多模型对比验算并加强构造配筋很有必要性。

（3）竖向荷载作用下，由于上部剪力墙体与下部转换梁竖向变形相协调，产生整体弯曲变形，导致转换梁上一层剪力墙应力突变，墙体水平向产生较大拉（压）力，平面内产生较大弯矩和附加轴力，墙体配筋建议根据应力计算结果验算复核，轴压比建议按照斜截面组合压力验算。

（4）由于转换梁上一层剪力墙受力复杂，设计上建议墙体加厚，尽量避免墙体开洞，避免采用一字形墙肢。