Stein矩阵方程的位移型全局Hess方法和CMRH方法
熊 露,张 婷,李胜坤
(成都信息工程大学 应用数学学院,四川 成都 610225)
0 引言
本文讨论一般的大型稀疏Stein矩阵方程
X+AXB=C
(1)
的数值解法,其中系数矩阵A∈n×n,Β∈s×s,C∈n×s是给定的矩阵,X∈n×s是待求的未知矩阵.方程(1)存在唯一解的充分必要条件为λi(A)λj(B)≠-1,其中λi(A),λj(B)分别是矩阵A,B的特征值[1].
Stein矩阵方程是一类特殊的矩阵方程,在离散时间系统、概率、统计、光谱分析,神经网络和图象复原等领域有着广泛应用[2-9].同时Stein矩阵方程也是控制系统设计的计算工具[10].因此,求解Stein矩阵方程显得尤为重要.
对于低阶稠密的Stein矩阵方程,通常采用Kronecker积将其转化为线性方程组后直接求解.由于实际问题产生的Stein矩阵方程通常都是高阶稀疏的,因此迭代法[11-13]具有更大的优势.对Stein矩阵方程而言,系数矩阵间阶数的不同对迭代法的构造有着重要的影响.
近年来,一些求解不同类型Stein矩阵方程的迭代方法相继被提出.当矩阵B的阶数远远小于矩阵A的阶数时,文献[14]利用块Arnoldi正交化过程和非对称块Lanczos双正交化过程将Stein方程降阶后直接求解,提出了块Arnoldi型Stein方法和非对称块Lanczos型Stein方法.文献[15]则采用推广的块Arnoldi型方法降阶求解.对低秩Stein矩阵方程,即矩阵C=EFT的秩很小时,文献[16-17]利用全局Arnoldi正交化过程对Stein矩阵方程降阶求解,提出了Stein全局Arnoldi算法,得到其低秩解.块Arnoldi型正交化方法[18],推广的块Arnoldi型正交化方法[15],块Hessenberg型方法[19]也相继被提出.对于一般的Stein矩阵方程,文献[20]提出了Smith型迭代法求解Stein矩阵方程,但是这种方法对系数矩阵有一定的要求,即当ρ(Α)ρ(B)<1时方法才收敛,其中ρ(Α)和ρ(B)分别表示矩阵A和B的谱半径.文献[21]利用全局Arnoldi正交化过程提出了全局FOM(the global full orthogonalization method)和全局GMRES算法(the global generalized minimal residual).文献[22]利用矩阵Krylov子空间的位移不变性,提出了位移型全局FOM和位移型全局GMRES算法,降低了全局FOM和全局GMRES算法的计算量.
Hessenberg过程[23]是另外一种构造Krylov子空间基的方法,通常比Arnoldi正交化过程需要更少的计算量.紧接着,块Hessenberg过程[19,24]和全局Hessenberg过程[25-26]相继被提出.本文基于全局Heseenberg过程,提出了位移型全局Hess方法和位移型全局CMRH方法求解Stein矩阵方程.数值结果表明新方法相对于位移型全局Arnoldi型方法而言占有一定的优势.
对给定的两个实矩阵X,Y∈m×n,定义Frobenius内积为〈X,Y〉F=tr(XTY),相应的F范数用‖·‖F表示.如果〈X,Y〉F=0,就称X,Y正交.另外,X⊗Y=[xijY]∈mm×nn表示矩阵X和Y的Kronecker积.
为方便叙述,定义算子
M:X→AXB,
即方程(1)等价转化为
X+M(X)=C.
(2)
1 全局Hessenberg过程
本节介绍全局Hessenberg过程构造矩阵Krylov子空间的基的过程.
给定矩阵V∈n×s和算子M,定义矩阵Krylov子空间
Km(M,V)=span{V,M(V),…,Mm-1(V)},
其中,Mi(V)=M(Mi-1(V)),i=2,…,m-1.
全局Hessenberg过程构造基{V1,V2,…,Vm}满足的正交条件为:
Vk+1⊥FY1,Y2,…,Yk,k=1,2,…,m,
即
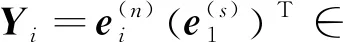

算法1 全局Hessenberg过程[24-25]1.令θ=
假设算法1在第m步之前不中断,则算法1生成的V1,V2,…,Vm构成Krylov子空间Km(M,V)=span{V,M(V),…,Mm-1(V)}的一组非正交基.
若Zm∈Km(M,V),则Zm可以表示为
其中,

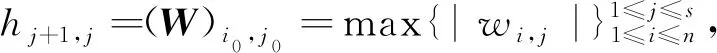

算法2 带主元策略的全局Hessenberg过程[24-25]1.定义i0,j0,满足(V)i0,j0=max{|vi,j|}1≤j≤s1≤i≤n;2.θ=(V)i0,j0,V1=V/θ;p1,1=i0,p1,2=j0;3.Forj=1,2,…,m do4.W=M(Vj);5.Fori=1,2,…,j do6.hi,j=(W)pi,1,pi,1;7.W=W-hi,jVi;8.Endfor9.定义i0,j0,满足(W)i0,j0=max{|wi,j|}1≤j≤s1≤i≤n;10.hj+1,j=(W)i0,j0;11.Vj+1=W/hj+1,j;12.pj+1,1=i0,pj+1,2=j0;13.Endfor
不难看出,全局Hessenberg过程(算法2)构造搜索空间
Km(M,V)=span{V,M(V),…,Mm-1(V)}的基V1,V2,…,Vm满足:

因此,下列关系式成立.
定理1令
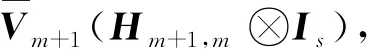
(3)
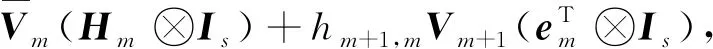
(4)
其中,em=(0,…,0,1)T∈m.
2 位移型全局Hess算法
本节给出求解Stein矩阵方程(2)的位移型全局Hess算法.给定初始近似值X0∈n×s,R0=C-X0-M(X0)为相应的残差.为了能够充分利用初始值的相关信息,第m步迭代解Xm在仿射空间X0+Km(M,R0)中寻找,即Xm∈X0+Km(M,R0),使得残差Rm满足
Rm⊥FY1,Y2,…,Ym.
利用全局Hessenberg过程(算法2),可构造矩阵Krylov子空间Km(M,R0)的一组基V1,V2,…,Vm,从而

相应残差为
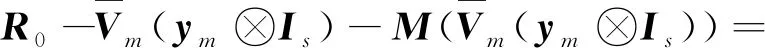
根据正交条件Rm⊥FY1,Y2,…,Yk,k=1,2,…,m,可得
(Im+Hm)ym=θe1,
从而

在实际计算时,随着迭代步数m的增加,算法的计算量和存储量会增加.因此,采用固定步数(m步)的重启型,相应的位移型全局Hess算法(简记为SGl-Hess(m))描述如下:

算法3 SGl-Hess(m)1.选择初始近似矩阵X0和精度ε;2.计算R0=C-X0-M(X0);3.运行算法2,得到一组基V1,V2,…,Vm和Hm;4.计算(Im+Hm)ym=θe1,得到ym;5.计算Xm=X0+Vm(ym Is),Rm=C-Xm-M(Xm);6.若‖Rm‖F<ε,停止迭代,输出Xm,否则继续;7.令X0=Xm,R0=Rm,返回步骤3.
3 位移型全局CMRH算法
本节构造位移型全局CMRH算法求解Stein矩阵方程(2).同样的,给定初始近似值X0,R0为相应的残差.第m步迭代解


其中,
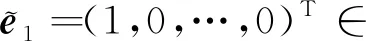
这里,ym采用极小化‖Rm‖F来计算,即


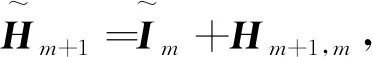
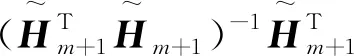

类似于位移型全局Hess算法,位移型全局CMRH算法(简记为SGl-CMRH(m))描述如下:

算法4 SGl-CMRH(m)1.选择初始近似矩阵X0和精度ε;2.计算R0=C-X0-M(X0);3.运行算法2,得到一组基V1,V2,…,Vm和Hm+1,m;4.计算miny∈Rm‖θ e1-I~my-Hm+1,my‖2,得到ym;5.计算Xm=X0+Vm(ym Is),Rm=C-Xm-M(Xm);6.若‖Rm‖F<ε,停止迭代,输出Xm,否则继续;7.令X0=Xm,R0=Rm,返回步骤3.
下面给出位移型全局CMRH算法的残差范数与位移型全局GMRES算法的残差范数之间的一个关系.
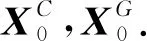
其中


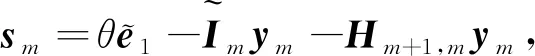
由范数的性质可得
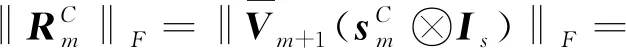
由最小范数条件可得

因此,

4 数值算例
下面给出两个数值算例说明位移型全局Hess算法(SGl-Hess(m))和位移型全局CMRH算法(SGl-CMRH(m))的有效性,并且与位移型全局FOM(SGl-FOM(m))和位移型全局GMRES方法(SGl-GMRES(m))[22]在迭代步数和计算时间等方面进行比较.所有数值计算都是用Matlab R2012a编程.在所有的数值算例中,选择的初始近似矩阵X0为零矩阵,停止迭代的条件为‖Rm‖F<10-8或者重启次数不超过200次.

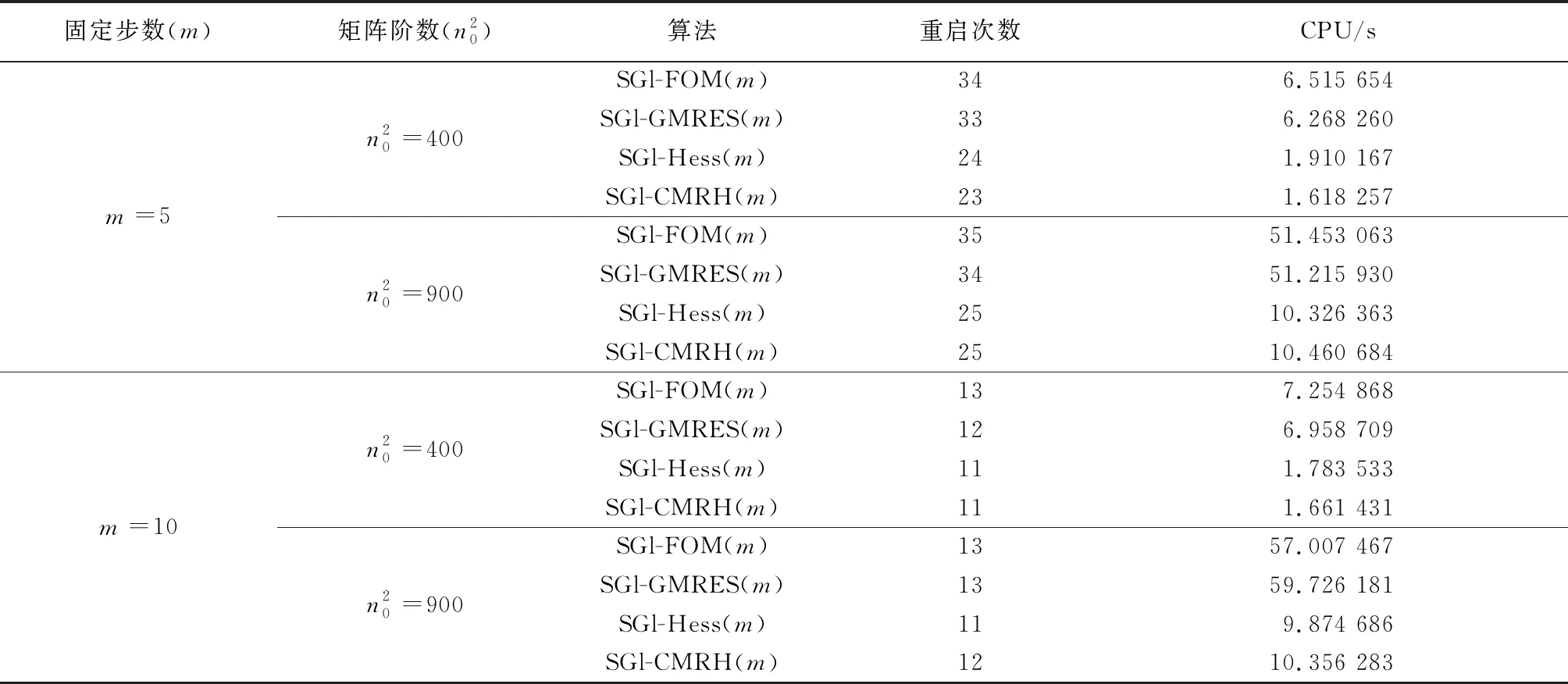
表1 例1的数值结果
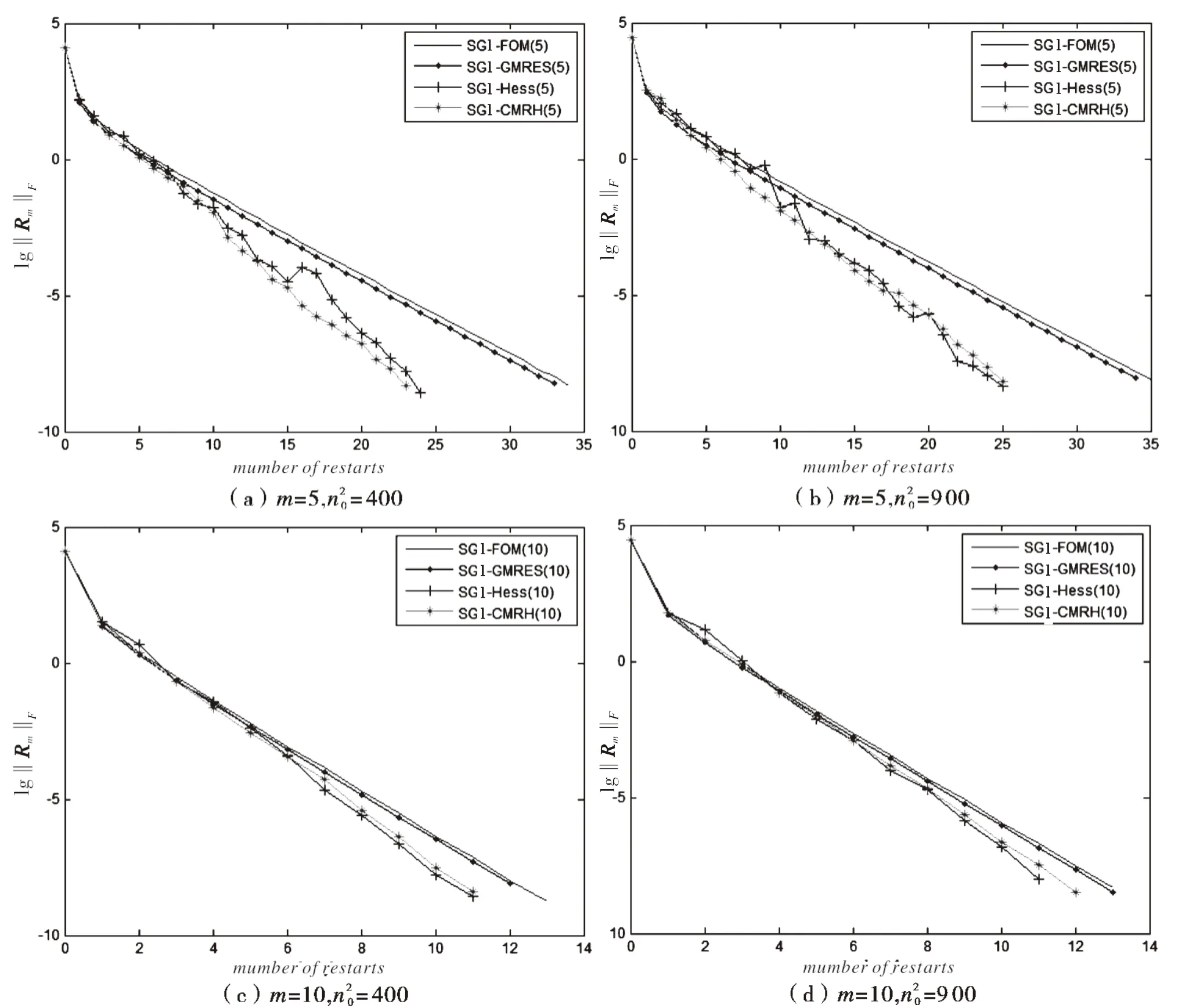
图1 例1的收敛曲线
通过表1可以看出,在给定的相同停止迭代条件下,SGl-Hess(m)和SGl-CMRH(m)方法在迭代步数上略少于SGl-FOM(m)和SGl-GMRES(m)方法,但是在CPU运行时间方面的优势非常明显.原因在于全局Hessenberg过程比全局Arnoldi正交化过程的计算量小,在迭代步数相差不多的情况下,运行时间更少.另外通过图1可以看出,SGl-Hess(m)方法的残差光滑性比其他三种方法稍微差点.
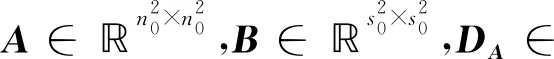

矩阵C的选取满足精确解X=I∈n×s.在这里,取
固定步数分别取m=5和m=10,计算结果见表2和图2.

表2 例2的数值结果

图2 例2的收敛曲线
通过表2可以看出,SGl-Hess(5)和SGl-CMRH(5)方法在重启次数和CPU运行时间方面都优于SGl-FOM(5)和SGl-GMRES(5)方法;SGl-Hess(10),SGl-CMRH(10),SGl-FOM(10)和SGl-GMRES(10)方法的迭代次数相当,但CPU运行时间方面SGl-Hess(10)和SGl-CMRH(10)方法明显优于SGl-FOM(10)和SGl-GMRES(10)方法.图2表明SGl-Hess(m)方法的残差出现一些微小的震荡.
5 总结
基于全局Hessenberg过程,利用矩阵Krylov子空间的位移不变性,构造了新的算法,提出了位移型全局Hess算法和位移型全局CMRH算法求解一般的大型Stein矩阵方程,给出了相应的残差估计.数值例子表明,新方法相对于SGl-FOM(m)和SGl-GMRES(m)方法而言,在运行时间和迭代步数上占有一定的优势.

