基于坡道的城际铁路节能操纵策略

刘 彧

（浙江杭海城际铁路有限公司，浙江海宁 314499）

随着城市空间的拓展，大城市逐渐发展到城市与周边城市融合发展的都市区形态，城际铁路的发展有利于融入国家发展规划、促进区域经济发展、提升综合交通质量、完善交通建设规划[1]。列车运行过程中影响牵引能耗的因素有很多，线路类型、列车性能、站间距大小、线路横纵断面设计均会对牵引能耗产生影响。城际铁路站间距、正线长度较地铁更长，线路包含更加丰富的坡道特征。因此，通过优化列车节能操纵策略，合理的利用线路坡道信息，能够有效降低列车牵引能耗，减少轨道交通运营企业的能耗成本支出，对贯彻国家节能减排政策具有重要意义。

1 坡道节能操纵策略

1.1 既有研究的不足之处

目前，国内外已有大量研究对节能操纵策略进行描述。文献[2]以最大牵引力的牵引终止位置和初次巡航终止位置为决策变量，以列车运行牵引能耗最小为优化目标，采用加入邻域搜索策略的改进遗传算法和Brute Force算法求解改进操纵模型。宋文婷等学者构建定时约束下的列车操纵模型，引入组合优化技术，通过遗传算法为子区间搜索最优的速度码组合序列，将模型求解转换为最优化问题[3]。文献[4]提出列车在起伏坡道和时间约束下的两阶段双层列车节能优化方法，利用优化粒子群算法全面搜索列车最优节能驾驶曲线，同时对列车运行时间进一步分配与优化。HOWLETT等学者利用一种改进的能量最小化原理计算陡坡轨道上全局最优策略的临界切换点，用于计算工况最佳转换点[5]。丁勇提出在起伏坡道与定时约束条件下地铁列车节能运行的两阶段优化方法[6]。

城际铁路列车控制信号系统多采用嵌入式系统，列车运行具有大延时、多目标、多约束、非线性的特点，包含多种噪声，控制复杂度较高。然而，目前的研究方法一类使用精确模型对车辆被控对象及控制策略进行建模并求解，另一类方法使用人工智能等复杂算法对控制策略进行寻优。前者不能良好的应对存在大量噪声、实时性高、不宜频繁调节的工程应用场景；后者计算量较大，不适用于嵌入式系统，因此多用于离线计算，输出工况转换点等关键信息后，再应用于嵌入式系统的实时计算。

本文设计实现一种具有普遍适应性的在线坡道节能操纵策略，能够有效地解决传统节能算法无法直接应用于工程实际的问题。

1.2 降低牵引能耗的关键点

对于自动驾驶系统来说，其核心功能就是计算最佳运行速度目标，并通过控制列车的牵引、制动系统使列车在自动驾驶的全过程有效地跟踪并达成命令速度曲线，所以合理有效的控制策略和控制算法应该在综合评估运行表现的基础上，平衡列车运行能耗、列车运行效率等运营要求。运行效率最高的列车控制由最大牵引、巡航、最大制动阶段构成，在线路条件允许下，列车按照最大允许速度行车，列车的牵引能耗最大。节能最优操纵策略则应包含最大牵引、巡航、惰行、最大制动4个阶段[7]。因此，节能操纵策略的关键点可以转化为寻找牵引-惰行工况转换点的问题，将部分牵引工况转换为惰行工况。

1.3 坡道节能操纵策略

当列车惰行行驶在同一坡道内时，列车的加速或减速趋势由坡道值及阻力特征决定，在列车速度变化范围较小时，可等效认为列车始终保持相同的加速度或减速度不改变。同时，若列车从当前位置惰行至坡道终点时，如果列车速度仍然在坡道终点的运行速度允许范围之内，则列车当前位置就可以作为工况转换点，开启惰行至坡道终点。

如图1所示，以单上坡为例，计算坡道终点的命令速度Vcmd和从列车当前位置惰行至坡道终点的列车速度V。若(V+Para)≥Vcmd，则当前位置至上坡终点不需要加速。Para为速度波动允许阈值。同理，如图2所示，以单下坡为例，计算坡道终点的命令速度Vcmd和从列车当前位置惰行至坡道终点的列车速度V。若(V+Para)≥Vcmd，则当前位置至下坡终点不需要加速。

图1 单上坡惰行策略Fig.1 Single uphill coasting strategy

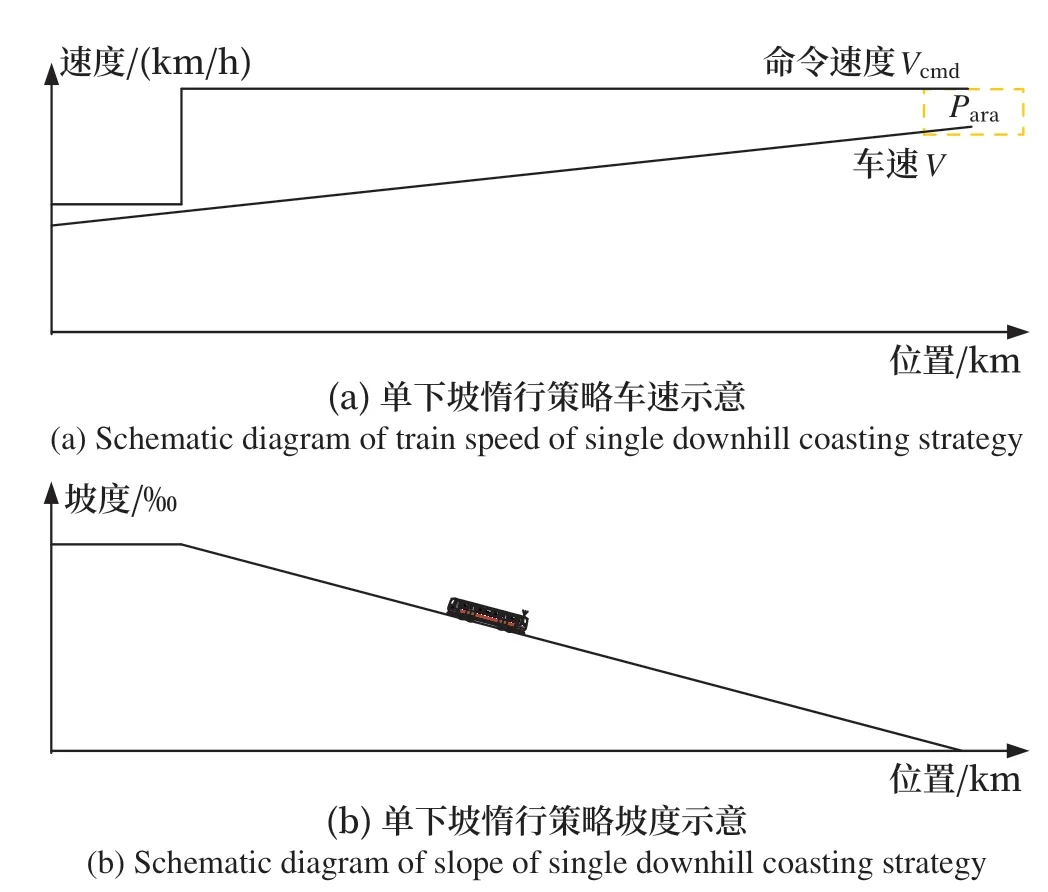
图2 单下坡惰行策略Fig.2 Single downhill coasting strategy

针对多坡道，计算当前位置惰行至各个坡道终点的速度，以及各个坡道终点的命令速度，只要存在一处满足(V+Para)≥Vcmd，则不需要加速。如图3所示，依次计算惰行速度V1～V4。若存在一处满足(V+Para)≥Vcmd，则允许列车进入惰行工况。

图3 多坡道惰行策略Fig.3 Multi ramps coasting strategy

2 列车速度预测

列车速度预测的目的是判断列车以当前位置、当前速度惰行至某位置时，该位置的命令速度与列车速度的差距是否满足要求。本文考虑列车为多质点物体，使用惯性质量、静态质量、基准点势能差、能量守恒计算列车处于多个坡道段时的能量。

能量守恒公式：

Mi代表动态或惯性质量，是静态质量Mp和与惯性相当的质量Mrot的和。如图4所示，解释等效坡道的速度预测方法，车长为L，重力加速度为g，B点车头位置PB，A点车头位置PA，阻力Rf，各弯道的曲线附加阻力Rcramp，各弯道对应的长度Lcramp。

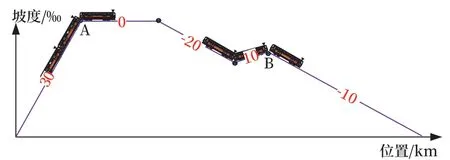
图4 等效坡道动能计算示意Fig.4 Schematic diagram of equivalent ramp kinetic energy calculation

如图4所示，假设A点为势能基准点，速度为VA，列车处于30‰坡的车长为LA1，重心高度为：

车辆动能为：

车辆势能为：

假设B点为势能基准点，列车位于-10‰坡道的车长为LB1，重心高度为：

列车位于10‰坡道的车长为LB2，重心高度为：

列车位于-20‰坡道的车长为LB3，重心高度为：

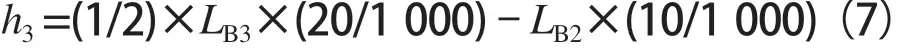
车辆势能为：

考虑基本阻力和弯道影响，B点动能为：

据此可计算从A 点惰行至B点的速度。

3 节能效果评价

ATO运行模式曲线优化是一个具有高实时性、多目标、控制对象非线性等特点的多目标优化问题[8]，通过减少牵引工况进行节能的同时会带来运行效率的下降。另一方面，各个城市、各条线路的坡道特征不同。因此，基于坡道的节能控制，需要在给定线路条件及运行效率的情况下，评价其效果。本文采用真实车辆牵引能耗功率数据，对列车能耗曲线进行建模，并使用仿真实验验证本文提出方法的效果。节能效果示意如图5所示。

图5 节能效果示意Fig.5 Schematic diagram of energy saving effectiveness

如图6所示，采用杭海城际线某区间数据绘制牵引能耗与运行时间关系图，随运行时间增大，牵引能耗明显下降。

图6 杭海线某区间牵引能耗/(kW/h)-运行时间/s关系Fig.6 Relationship between traction energy consumption/ (kW/h) and running time/s on a section of Hang-Hai line

4 结束语

本文提出一种基于坡道的节能运行控制策略，能够在线实时计算列车是否可以进入节能工况，并使用杭海城际铁路数据进行节能效果验证。数据显示，随着运行时分的增加，牵引能耗显著降低。本文所提出方法计算简便，能够应用于嵌入式系统，在列控信号系统节能应用方面具有实用价值。