基于本地化差分隐私保护的频繁项目挖掘算法
朱美琪,杨 庚,白云璐
(1.南京邮电大学 计算机学院、网络空间安全学院,江苏 南京 210023;2.江苏省大数据安全和智能处理重点实验室,江苏 南京 210023;3.南京市医药大学 信息技术学院,江苏 南京 210023)
0 引 言
频繁项目挖掘(frequent items mining)是当前数据挖掘研究的热点问题之一,其算法的核心是找出数据集中频繁出现的项。top-k频繁项目挖掘[1]是挖掘出前k个频繁出现的项。该思想已广泛运用到现实生活中。例如,视频网站可以通过对所有用户观看的影片进行记录、分析,然后向用户推荐本周最受欢迎的前十个电影。在记录用户信息的过程中,如果不做任何隐私保护措施,最后的推荐结果可能会有很高的准确性,但会严重侵犯用户的隐私。因此,在保证用户隐私性的同时要保证挖掘结果的准确性已经成为数据挖掘领域亟待解决的问题之一。
差分隐私[2]作为一个有效的隐私保护机制,现已广泛运用到浏览器、系统等应用中。例如Apple的IOS系统和Google的Chrome都运用了差分隐私的思想来保护用户的隐私。差分隐私又分为中心化差分隐私与本地化差分隐私,其中中心化差分隐私技术中,算法的隐私性通过临近数据集来定义,因此其要求一个可信的第三方数据收集者对数据分析结果进行隐私化处理,而对于本地化差分隐私技术而言,每个用户能够独立地对个体数据进行处理。目前已经有了许多关于本地化差分隐私的频繁项目挖掘算法,例如Zhan Qin提出的LDPMiner[3-4]算法,该算法在保护用户隐私的同时,比较了当前已有的满足本地化差分隐私的保护算法,并对其进行优化,在一些真实数据集上有较好的表现。但该算法在面对大量用户的真实数据挖掘的问题时,面临了一些新的挑战:(1)因为用户量的增大,挖掘的时间复杂度也随之增大;(2)可以对用户进行分组挖掘来降低时间复杂度,但同时需要保持挖掘结果的可用性。所以,如何在保证时间复杂度降低的同时也能提高挖掘频繁项目的可用性就成了研究的关键所在。因此,该文通过基于本地化差分隐私保护,对用户进行分组挖掘的思想,设计了一种频繁项目挖掘的算法GFIM(group-based frequent items mining)。
主要贡献如下:
(1)为了提高挖掘频繁项目的可用性,设计了一种基于分组思想的满足本地化差分隐私挖掘算法,并在理论上证明了该算法满足ε-本地化差分隐私,多个真实数据集上的实验表明该算法的性能要优于LDPMiner算法。
(2)在GFIM算法中,采用将整个运行过程分成两个阶段、用户数据分为两组的策略,在保证高可用性的同时,减少了挖掘时计算的次数,从而加快了挖掘数据的时间,达到了优化算法时间复杂度的效果。
1 相关工作
在Warner首次对随机响应的方法进行研究[5]之后,研究者们开始探索其他扰动机制。Hsu等[6]集中在基于随机投影和测度集中的技术来估计频繁项目。继这项工作,Bassily等[7]提出了一种有效的协议,用于SH(succinct histogram)估计与信息理论上的误差。为了处理隐私预算的问题,提出了RAPPOR[8-9],SH和RAPPOR的相关信息将在第二节进行介绍。此外,关于频繁项集挖掘的文献也很丰富。其中,有几篇与文中的研究方向有关。 Bhaskar等[10]提出了一种基于两阶段的方法,该方法使用截短的频率阈值来缩小频繁项集的候选列表。算法可以概括为如下两步:(1)计算出一个m值,从所有长度不大于m的候选项组成的集合C中挑选出top-k频繁项集;(2)对挑选出的k个项集的真实支持度添加拉普拉斯噪声后发布。该算法的问题在于第一步,因为其候选项集合C呈指数规模增大,即|C|=|I|m(|I|表示项集域的大小),若遍历C中所有项集,则每个项集能分到的隐私预算将会很少,计算结果将会很不准确。TF应用截断频率技术对C中项集进行筛选,只需遍历C中支持度大于fk-γ的项集(其中fk表示第k频繁项集的支持度真实计数,γ是调节参数)。在一般情况下,使用该技术可以对候选项集合C进行有效筛选,但是随着k值的增加,该筛选条件会被弱化,甚至失效。丁哲[11]为了从不确定的数据集中挖掘出基于期望支持度的前k个最频繁的频繁项集,并且保证挖掘结果满足差分隐私,提出了FIMUDDP算法。该算法利用差分隐私的指数机制和拉普拉斯机制确保从不确定数据中挖掘出的基于期望支持度的前k个最频繁的频繁项集和这些频繁项集的期望支持度满足差分隐私小的项,从而降低发布的频繁项集的支持度误差。
然而,所有上述机制都需要对数据集有全局了解,这使得它们不适用于本地化差分隐私。尽管上述已有工作并非所有针对中心化差分隐私的技术都适合于本地化差分隐私,但这些技术背后的思想仍有助于笔者设计符合LDP的算法。
2 理论基础
2.1 本地化差分隐私
近年来,本地化差异隐私作为一种区别于中心化差分隐私的隐私保护模式,引起了人们的广泛关注。它的隐私化处理发生在用户的本地设备中,用户对自己的个人数据进行加噪再发给数据收集者。数据收集者得到的是不准确的用户数据,这样能够避免不可信的第三方造成隐私的泄露。下面给出正式的定义:
定义1(ε-本地化差分隐私):假设有一个随机算法A,A的所有输出构成集合O,A的所有取值构成集合I,如果对于任意两条记录R∈I和R'∈I以及任意一个输出S∈O,存在:
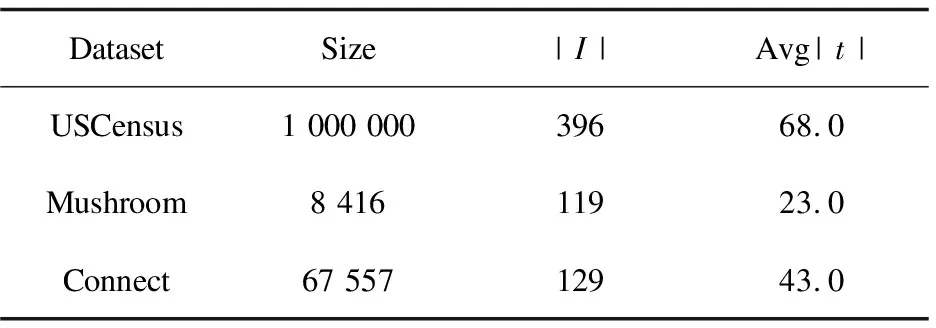
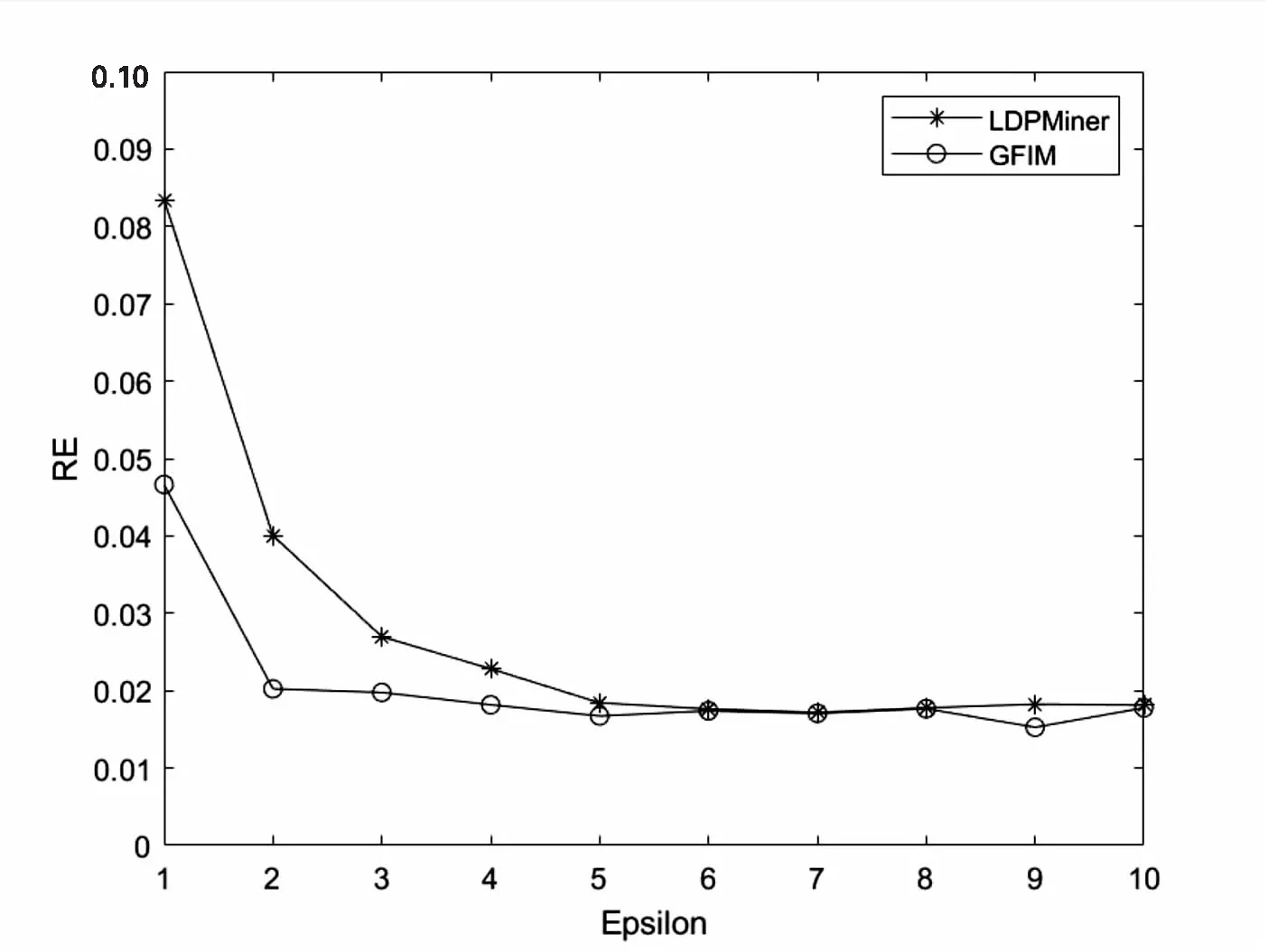
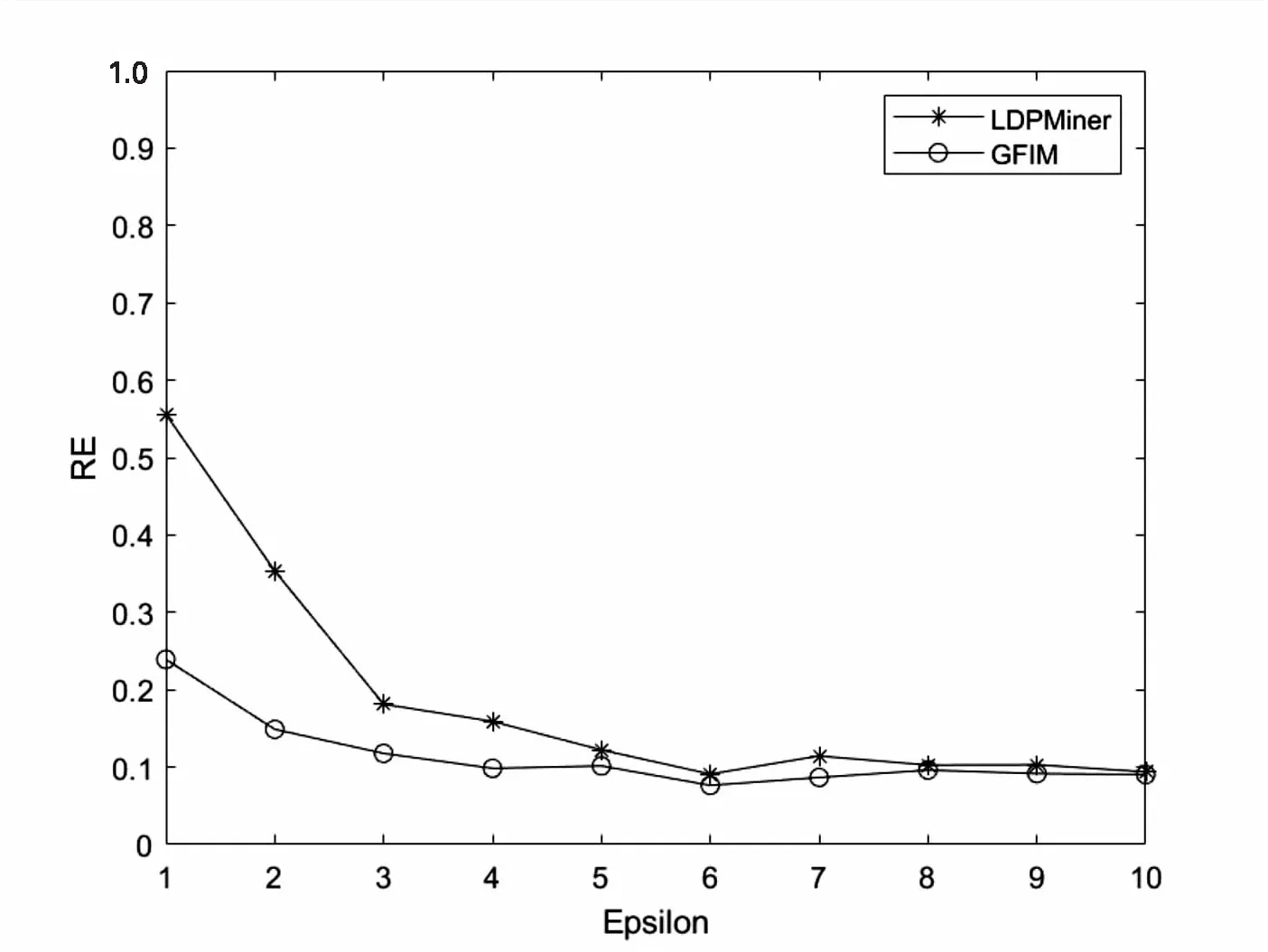
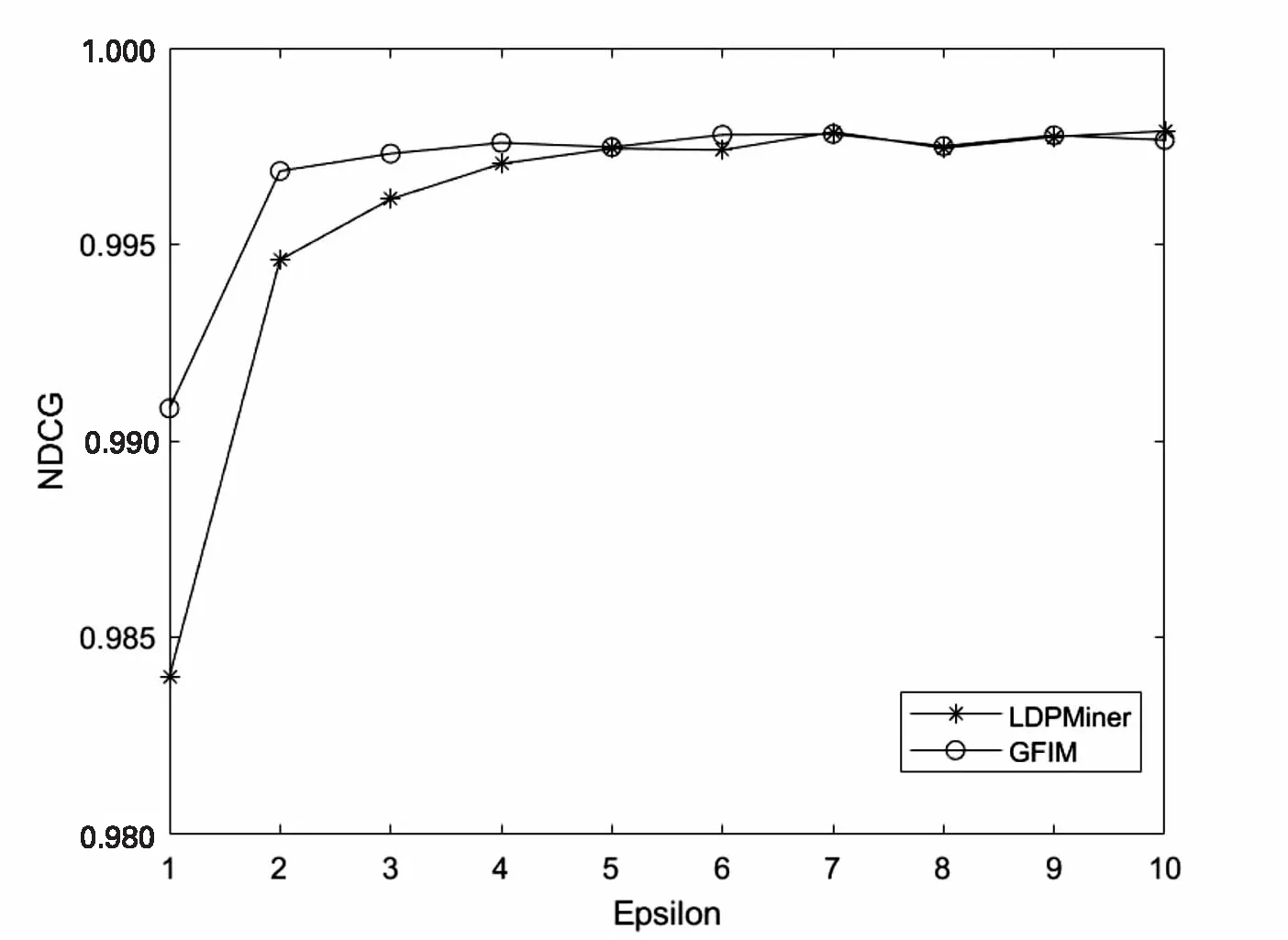
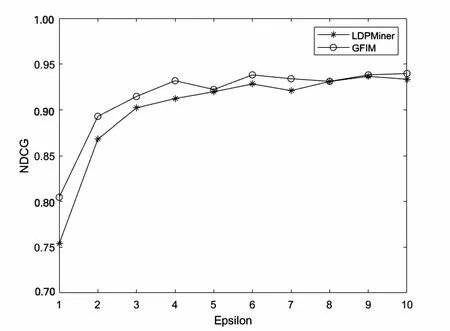
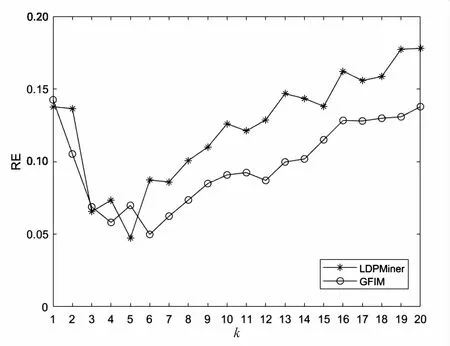
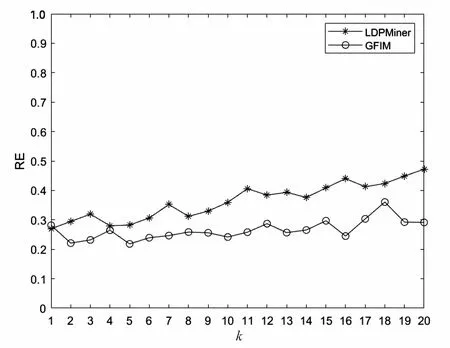
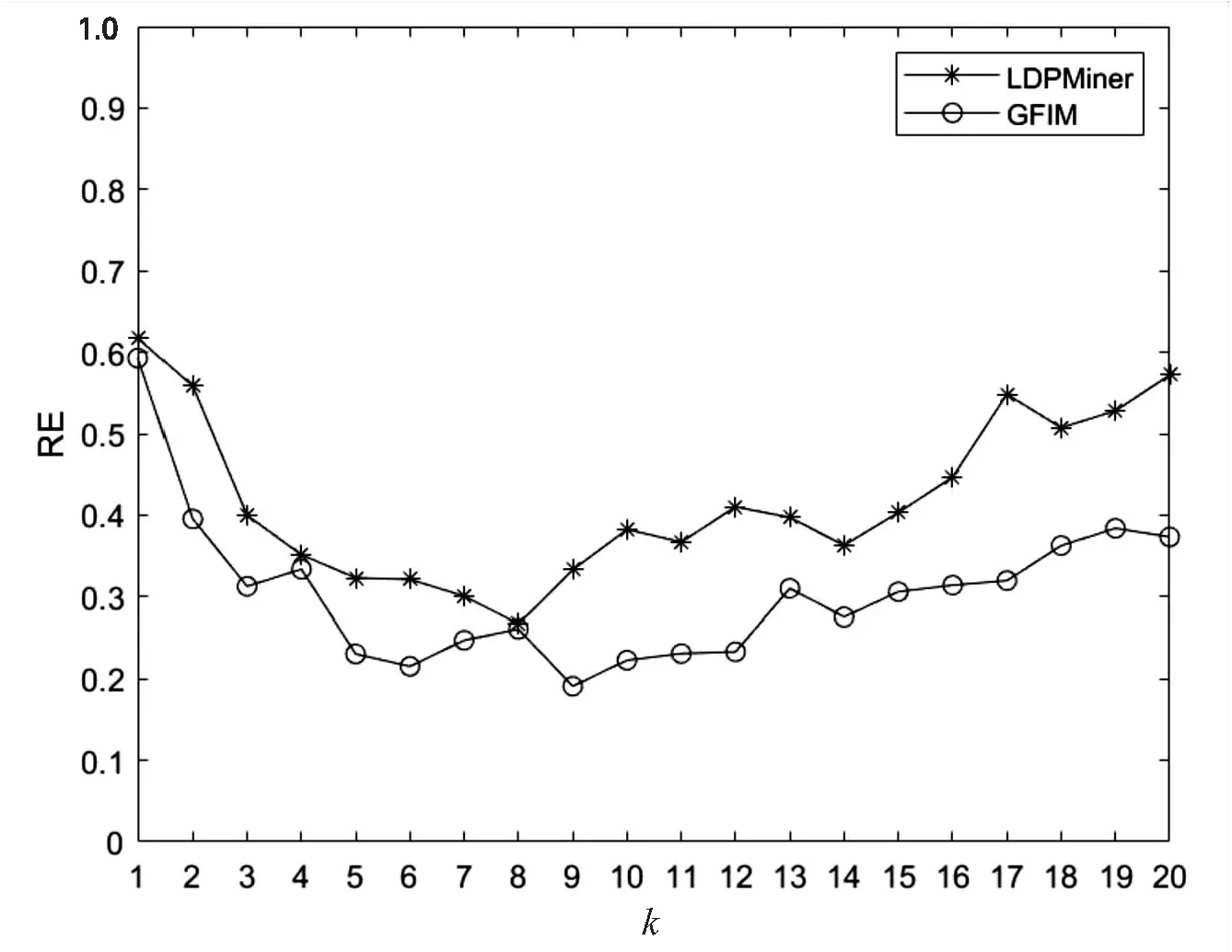
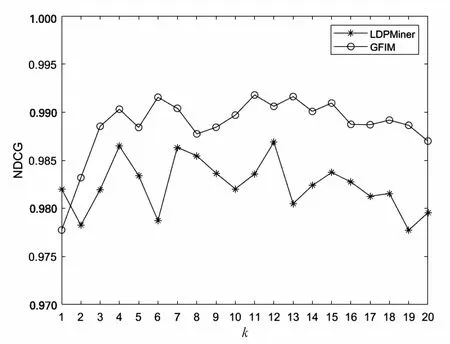
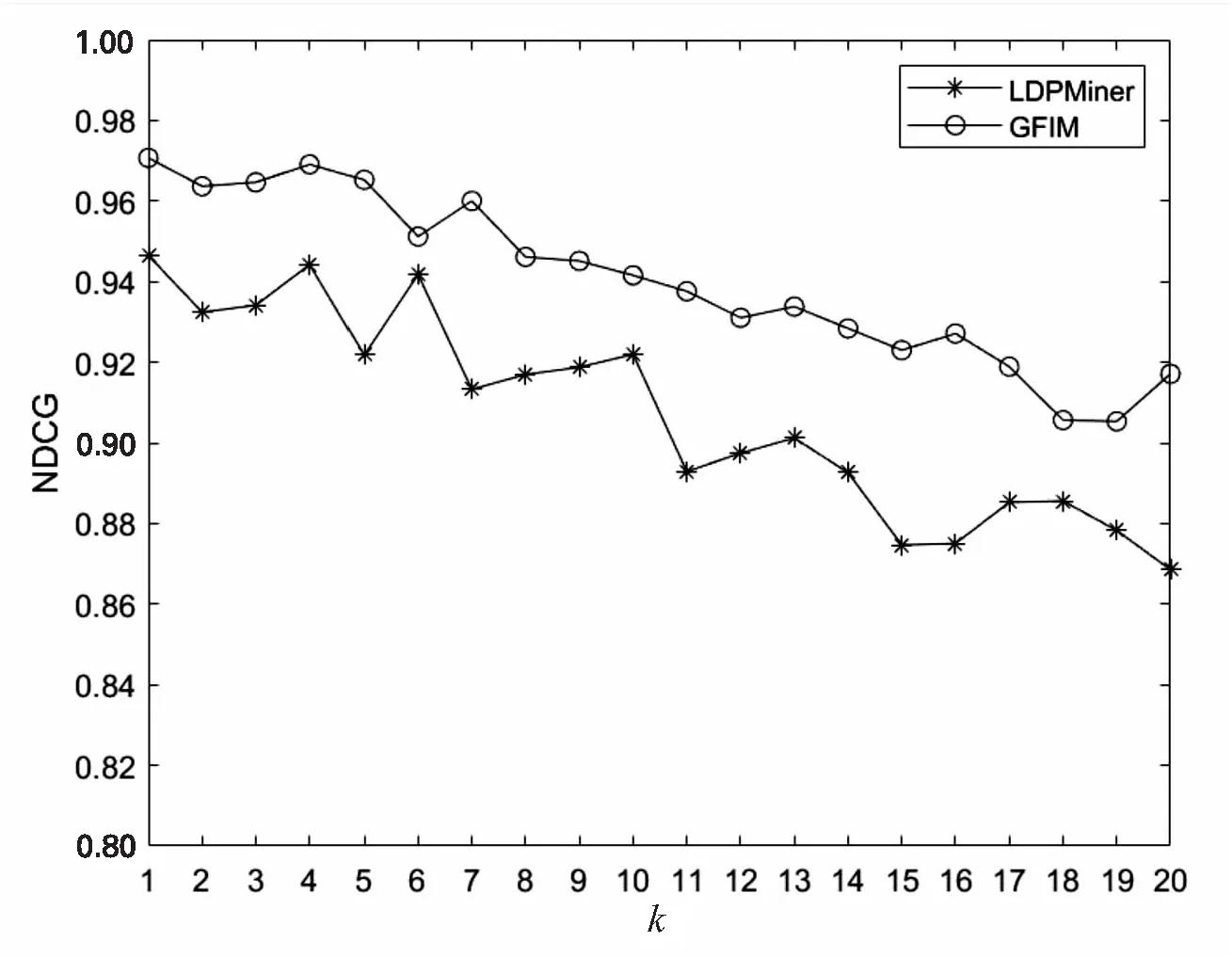
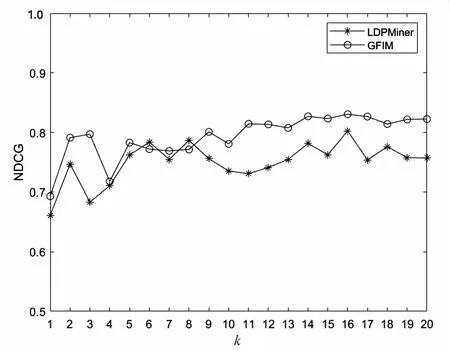
Pr(A(R)∈S) (1) 则称算法A满足ε-本地化差分隐私,其中ε称为隐私参数或隐私预算。 定义3(并行组合性):假设有随机算法A1,A2,…,An,其隐私参数分别为ε1,ε2,…,εn,当这些算法作用于不相交的数据集D1,D2,…,Dn时,这些算法构成的组合算法A(A1(I),A2(I),…,An(I))对这些数据集提供max(εi)-差分隐私保护。 此性质表明,当多个随机算法作用的数据集两两之间互不相交时,它们对所有数据集提供的隐私保护水平取决于max(εi)。特殊地,当A1=A2=…=An时,ε=εi,即当同一个算法多次作用于不相交的数据集时,隐私保护水平不变。 频繁项目挖掘是数据挖掘的研究热点问题之一,旨在找出频繁出现在事务数据集中的top-k项目。具体描述如下:如果一个数据流σ={a1,a2,…,am},其中m为数据流的大小,ai∈{1,2,…,n}。可以定义每个元素出现的次数为F=(f1,f2,…,fn),其中fi为第i个项目出现的次数。如果给定参数k,求top-k频繁项目,那么可以对F进行分析和统计,然后输出的前k个项目就是top-k频繁项目挖掘的过程。 2.3.1 随机响应解决方案 2.3.2 RAPPOR算法 2.3.3 Succinct Histogram算法 本节包括GHHE算法的概述及具体实现细节。GFIM分为两个阶段,并将隐私预算也分为两个部分用来完成这两个阶段,整个过程满足ε-LDP。第一阶段中,每个用户拥有l项,并在ε-DP下向数据收集者报告数据,数据收集者根据用户提交的信息挖掘出一个大小为kmax=O(k)的候选集C。第二个阶段,首先是对用户进行分组,第一组根据挖掘出的候选项集C,把自身拥有的却不在C中的项目设置为冗余项,然后把挖掘出的项集E报告给数据收集者;第二组是根据第一组挖掘出的项集E进行二次挖掘,最终得到top-k频繁项目。 算法1总结了GFIM算法完整的框架。其中1~2行属于预处理部分,3属于GFIM算法的第一阶段,4~6是GFIM算法的第二阶段。 算法1:GFIM算法。 Input:事务数据集D,k,隐私预算ε; Output:top-k频繁项目。 1.将隐私预算ε分为ε1和ε2; 2.计算真实的top-k频繁项集; 3.使用ε1的隐私预算来获取候选项集C; 4.将总用户数随机分成两组; 5.第一组数据使用ε2的隐私,以C为候选项集预算来获取项集E; 6.第二组数据同样使用ε2的隐私预算,以E为候选项集来获取top-k频繁项目。 阶段一是找出频繁项的候选集的过程。上文提到的RAPPOR和SH是两个经典的频繁项目挖掘算法,但它们不能直接运用于阶段一的场景,因为传统的RAPPOR和SH算法均要求每个用户的输入为一个项目,而在文中的场景中用户输入的是一个经过处理后的大小为l的项集。一个直观的解决方案是调用l次RAPPOR或SH,再把每次调用得到的估计频率累加得到最终的估计频率。这个想法是可行的,但也是低效的。对这种想法的一种改进方案是从每个用户的项集Si中随机选取一个项作为输入,然后采用RAPPOR或SH算法。已有的工作[2]证明了该想法的合理性,证明了其优于前面所说的调用l次RAPPOR或SH。但是,因为每个用户只向数据收集者发送一个随机的项而不是所有l个项,这样直接的随机抽取会导致有偏频率估计。为了达到无偏估计,需要将估计的频率乘以l。根据上文描述的RAPPOR和SH算法的对比分析,出于节约通信带宽和提高计算效率的考虑,这里将以SH算法为基础对其进行改造分析,改造后的算法称为抽样SH算法,抽样SH算法将作为阶段一和阶段二的基本算法。抽样SH算法与传统SH算法大体一致。同时,文中采用了一种正交矩阵生成的方法,假设d≪n,参考文献[9]证明了在d≪n的情况下采用正交矩阵取代完全随机矩阵能够提高SH的准确性。 算法2:抽样SH正交矩阵的生成。 Input:项的取值集合大小d; Output:正交矩阵φ。 1.计算m=2「log2d⎤ 2.S={[1,-1],[1,1]} 3.while |S| 4.S'=φ 5. forv∈Sdo 6.S'=S'∪{v‖v,v‖(-v)} 7. end for 8.S←S' 9. end while 10.N=S[1:m] 11.φ=NT 12. returnφ 算法3:抽样SH LR(local randomizer)(用户端部分)。 Output:干扰后的向量zi。 1.从项集Si中随机选取一个项i; 3.ifii=⊥ then 5. else 6. 生成一个标准的基向量eii∈{0,1}; 8.end if 9.returnzi 阶段二的场景与阶段一有所不同,不同之处有二:一是对总用户数进行了随机分组;二是每一组进行挖掘时的候选项集是不同的。针对这两点不同,需要设计出相应的解决方案。阶段二中依旧采用抽样SH作为算法的基础。显然,当候选项集合缩小时,SH中的随机矩阵也会相应缩小。这一方面减少了噪音,另一方面也降低了运算开销,最终会提高估计频率的准确性。针对第二个不同点,在用户端上的LR(local randomizer)做了以下调整:(1)第一组LR收到候选集C后,先求出用户原本的项集Si与候选集C的交集Ti;(2)如果交集N的大小小于kmax,补充若干个冗余项使其大小变为kmax,得到新项集Ni;(3)从Ni中随机选取一个项ii应用随机响应技术。第二组数据也要经历这样的过程,区别是第二组用户收到的不是候选项集C,而是第一组用户响应后的数据。这样处理的好处是能有效增大候选集中的项被抽中的概率,进而提高候选集中的项的估计频率准确性。一个例子能很好解释其中的原因:假设用户ui的原项集Si包含候选集C,Si的大小为l=60,C的大小为kmax=30;在未经过以上处理前,从Si随机抽取一个项,该项属于候选集的概率为1/2,但经过(1)~(3)步处理后,被抽中的项属于候选集的概率为1。可见,这样的处理是很有效的。并且,如果不对长度小于的交集Ti填充冗余项,Ti的大小直接暴露给用户,会给攻击者提供额外的信息,存在着隐私泄露的风险。阶段二中的抽样SH只能计算候选集中各项的估计频率。然而,真实的top-k项并不一定恰好都落到候选集中,为了解决这个问题,需要把两个阶段的结果综合利用起来。这里按以下公式得到最终各项的估计频率: (2) 需要说明的是,阶段二中处理的两组用户数据并不相交,为了保证两组数据与总数据满足同分布,必须保证划分数据时是随机划分的。 算法4:GFIM LR(用户端)。 Output:干扰后的向量zi。 1.求交集Ti=Si∩C; 2.if |Ti| 3. 往Ti中加入若干个冗余项得到新的用户项集|Ni|=kmax; 4.end if 5.从项集Ni中随机选取一个项ii; 7.ifii=⊥ then 9. else 10.生成一个标准的基向量eii∈{0,1}; 12.end if 13.returnzi 本地化差分隐私蕴含着两个极其重要的性质:序列组合性和并行组合性[15]。利用这两个性质,可以很容易地证明某种算法是否满足本地化差分隐私。 GFIM算法将隐私预算ε分为两部分,分配给算法的两个主要步骤:阶段一生成候选集ε1、阶段二分组计算频繁项目ε2。其中,选择ε1=0.6×ε,ε2=0.4×ε。 定理:GFIM算法满足ε-本地化差分隐私。 证明: (1)阶段一安全性证明。 (3) (4) 进而有: (5) 所以抽样SH算法满足ε1-本地化差分隐私,即阶段一满足ε1-本地化差分隐私。阶段一生成一个大小为kmax的候选集。候选项目集大小的选取至关重要。候选项目集太小的话,真实的频繁项可能会没有落在候选集内,导致估计的误差会增大;候选集过大,kmax有可能会大于l,同样会降低估计频率的准确性。 (2)阶段二安全性证明。 假设B为阶段二中第一组用户对数据的处理算法。B的输入是隐私参数ε2、用户ui的项集Si和候选集C。B首先对Si进行修剪得到Ni。之后B对Ni采用抽样SH算法,该处理过程用C表示。由阶段一的证明可知,C满足本地化差分隐私。假设S1,S2为任意两个未修剪前的用户项集,o表示B的任意输出。要证第一组用户对数据的处理算法满足ε2-本地化差分隐私,即证: (6) 因为修剪过程是确定的,所以有: Pr[B(S1,ε2,C)=o]=Pr[C(N1,ε2)=o] (7) 又C满足本地化差分隐私,有: (8) 由上述可知第一组用户对数据的处理算法满足ε2-本地化差分隐私。因为第二组用户对数据的处理与第一组原理相同,所以第二组对数据的处理也满足ε2-本地化差分隐私。又因为,这两组数据不相交,根据差分隐私的并行组合原理可知,整个阶段二满足ε2-本地化差分隐私。 由于阶段一,阶段二分别满足ε1和ε2-本地化差分隐私,由差分隐私的序列组合性知,ε=ε1+ε2。即,GFIM满足ε-本地化差分隐私,证毕。 实验环境为Inter(R) Core(TM) i5-3230M CPU2.60 GHz,4 GB内存,Windows10操作系统。算法均使用Python来实现。在三个真实数据集上进行了测试,这些数据集可从Spmf上下载。分别是USCensus(US Census 1990 dataset),Mushroom(UCI mushrooms dataset)和Connect(UCIconnect-4 dataset)。表1给出了每个数据集中的几种特征,包括事务数量、项集域大小以及平均事务长度。通过实验将LDPMiner算法与文中提出的GFIM算法进行比较,验证该算法的性能。 表1 三种数据集信息描述 为了评估两种算法的性能,采用了两个广泛使用的评价标准,即相对误差(RE)[16]和折扣累计增益(DCG),定义如下: (1)相对误差(RE):用来测量相对于频繁项目实际频率的估计频率的误差。具体来说,令V={v1,v2,…,vk}是前k个频繁项目的集合。 (9) (2)折扣累计增益(DCG):DCG测量数据收集者计算的频繁项目的质量[17]。频繁项目的频率排名列表中的项目vi的相关性或增益是通过相关性计算公式得出的: relvi= log2[|d-|rankactual(vi)-rankestimated(vi)||] (10) 可以直观地发现,vi的估计频率排名与真实频率排名越接近,相关性就越大。给定一个真实的前k个频繁项目V={v1,v2,…,vk},估计频率的排名的DCG计算为: (11) 折扣因子log2(i)可以赋予较高排名的项目更高的权重。通过将估计的排名列表与理想的DCG(IDCG,与实际的频繁项目排名完全一致)进行比较来进行归一化。 (12) 很容易从公式得出,NDCG的结果是在0到1之间,能够比较不同k值上计算的频繁项目的质量。 实验分为两个部分:(1)设定k=10,查看GFIM算法在不同的隐私预算下与LDPMiner算法的RE和NDCG性能对比。USCensus,Mushroom,Connect实验结果按顺序如图1(a)、(b)、(c)和图2的(a)、(b)、(c)所示。 (a)USCensus数据集 (c)Connect数据集 从图1可以看出,随着隐私预算ε的增大,相对误差RE在三个数据集上都是呈总体下降趋势,这符合差分隐私思想中隐私预算越大相对误差越小的性质。同时可以看出,隐私预算参数ε从0变化到10的过程中,改进后的GFIM算法在相对误差上的性能优于LDPMiner算法。 (a)USCensus数据集 (b)Mushroom数据集 (c)Connect数据集 从图中可以看出,随着隐私预算ε的增大,计算频繁项目的质量在三个数据集上都是呈总体上升的趋势,这与NDCG标准定义的理论结果相符。同时,隐私预算参数ε从0变化到10的过程中,改进后的GFIM算法在频繁结果质量上优于LDPMiner算法。 (2)设定隐私预算ε为固定值,观察GFIM算法在不同k值下的RE和NDCG与LDPMiner算法的对比。USCensus,Mushroom,Connect实验结果如图3(a)、(b)、(c)和图4(a)、(b)、(c)所示。 (a)USCensus数据集 (b)Mushroom数据集 (c)Connect数据集 图3中,根据不同的数据集大小设置了不同的隐私预算值。其中Mushroom的隐私预算ε设置为3,Connect和USCensus数据集隐私预算ε设置为1。根据曲线图可以看出,改进后的GFIM算法在相对误差上的性能优于LDPMiner算法。 从图4中可以明显看出,改进后的GFIM算法计算出的频繁项目的质量要高于LDPMiner算法计算出的频繁项目的质量。 (a)USCensus数据集 (b)Mushroom数据集 (c)Connect数据集 该文研究出一个既满足本地化差分隐私又有较高可用性的GFIM算法。整个加噪和挖掘频繁项目的过程划分为两个阶段。在第一个阶段,GFIM实现对整体用户的隐私保护和频繁项候选集的筛选;在第二个阶段,GFIM把用户划分为随机等大小的两组用户,把候选集发送给第一组用户,让用户对自身的项集重新进行打包和加噪,挖掘候选集内各项的频率,再把结果当成候选项集发送给第二组用户。最后,GFIM综合两个阶段得到最后频繁项目和对应频率。为了验证算法GFIM的可行性和对已有方案的改善,选取了LDPMiner算法进行对比,并在三个真实数据集进行多次实验。结果表明,GFIM能够较为准确地挖掘出频繁项目,并且在RE和NDCG这两个指标上的性能表现均优于LDPMiner算法。同时,在实验中发现,针对不同的数据集和不同的k值,kmax有对应的最适合的大小。kmax的大小会对实验结果有重要的影响,一个合适的kmax将极大地提高实验结果的准确性。另外,用户的分组问题也是个可以讨论的研究方向,文中方法是将用户随机等分成两组,可以尝试在用户分组上面再进行研究,观察是否能对频繁项目挖掘的性能有进一步的提高。
2.2 频繁项目挖掘
2.3 LDP解决方案
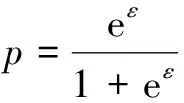
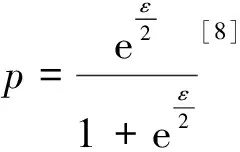
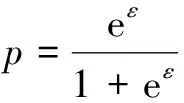
3 GFIM算法
3.1 GFIM算法概述
3.2 GFIM算法中阶段一分析设计

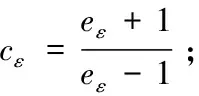

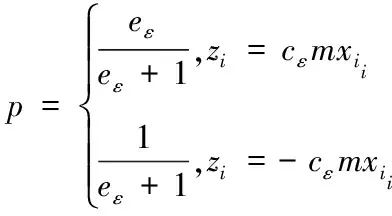
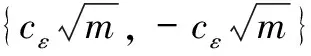
3.3 GFIM算法中阶段二分析设计
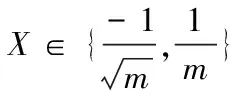
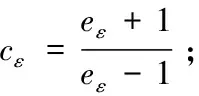

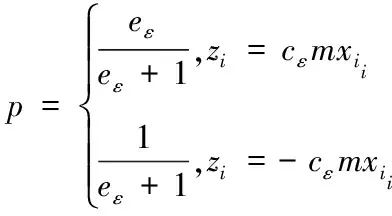
4 GFIM算法隐私保护性能分析
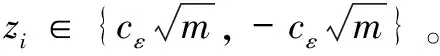
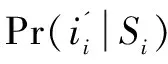
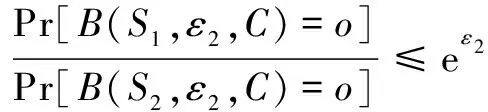
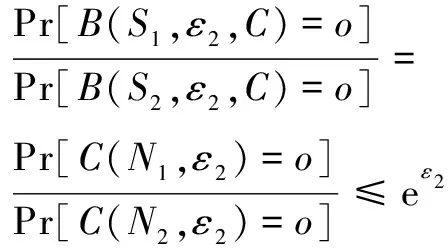
5 实 验
5.1 实验设置
5.2 实验结果与分析

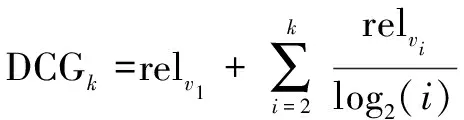
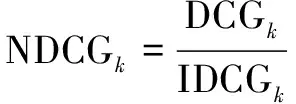

6 结束语

