超大直径盾构掘进引起地表纵向变形规律分析

方小明 张孟喜 张梓升 肖晓春 李磊

摘要：

为建立盾构掘进所引起地表变形的理论分析模型，从上海市北横超大直径盾构隧道工程现场地表纵向变形实测数据统计分析出发，采用有限元软件模拟盾构隧道施工，重点研究刀盘前方地表变形与施工参数间的相互关系。研究结果表明：当土体达到被动极限状态时，刀盘前方最大隆起值约为10 mm，隆起形式近似为二次抛物线;同一埋深比情况下，刀盘前方最大隆起值与支护比成正比;同一支护比情况下，随着埋深比的增大，隆起范围逐渐远离刀盘向前移动，两者变化关系成正比，说明刀盘前方地表的隆起程度及隆起范围分别与施工参数中的支护压力及覆土厚度存在一定关系。根据对有限元模拟结果的分析，并通过数学推导，提出了预测盾构掘进引起地表纵向变形的理论模型。经过工程算例验证，该理论模型预测结果与北横通道现场实测数据吻合情况较好。

关 键 词：

地表变形; 盾构隧道; 盾构掘进; 有限元分析

中图法分类号： U455.43

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2021.07.027

0 引 言

随着城市化进程加快，地下空间的开发规模逐步扩大，盾构法已经成为中国隧道开挖的主要施工方法。盾构法施工质量的主要控制因素为地表变形，因此盾构施工过程及工后地表的变形机理与控制一直受到学界广泛关注。在行业内一般将直径大于14 m的断面称为超大断面。超大直径盾构施工过程中由于开挖土体体量大，对土体扰動大，导致地表变形较大，对穿越建筑物损坏影响大。因此超大直径盾构隧道掘进过程中对地表变形预测尤为重要。

盾构掘进引起地表变形的大致分布规律见图1。依据盾构法施工的开挖工序与变形机理，一般可以将盾构掘进过程引发的地表变形分为4个阶段[1-3]，如图1所示。

Ⅰ、Ⅱ阶段地表变形发生在刀盘前方，主要通过调节刀盘支护压力、排土量、掘进速度进行控制;Ⅲ阶段地表变形发生在隆沉分界点至刀盘正上方之间，由地层损失引起，影响参数主要是刀盘与盾壳外径的差距;Ⅳ阶段地表变形出现在盾构刀盘正上方及其后部分，由土体固结沉降引起，主要通过注浆进行控制[4-7]。目前为止，对于Ⅰ、Ⅱ、Ⅲ阶段的地表变形，仍没有较好的规律总结与理论计算模型，而对于Ⅳ阶段的地表变形，目前已有不少实用的理论计算方法。林存刚等分析了杭州市庆春路过江隧道泥水盾构施工地面沉降监测数据，提出了修正双曲线模型以预测地面总体沉降，经过实测数据拟合认为预测精度高于传统双曲线模型[8-11]。从盾构法的施工特点上看，经过上述4个开挖阶段后最终地表变形往往表现为沉降，但实际工程中为避免过度沉降带来的危害，常通过适当提高支护压力，使刀盘前方地表略微隆起，以抵消后期的部分地层损失，减少最终的地表沉降[12-15]。

大直径盾构隧道施工对地层的影响受到多因素特别是地层与施工参数的控制。施工参数繁多，现有研究成果比较繁杂，本文仅采用支护压力以及覆土厚度施工参数的简化方法来开展研究。

本文从超大直径盾构隧道工程现场地表纵向变形实测数据统计分析出发，分析盾构开挖引起地表纵向变形机理。由于Ⅰ、Ⅱ阶段刀盘前方地表变形影响因素较多，故通过建立三维有限元模型，认为刀盘前方地表的隆起程度及隆起范围分别与施工参数中的支护压力及覆土厚度存在一定关系。对于Ⅲ阶段，主要是刀盘和盾壳外径的差距起主要作用。Ⅳ阶段根据已有双曲线模型结合现场数据进行拟合。

根据Ⅰ、Ⅱ阶段的理论预测公式进一步推导Ⅲ、Ⅳ阶段的曲线模型，因此Ⅰ、Ⅱ阶段曲线模型是Ⅲ、Ⅳ阶段的基础，需要进行数值模拟分析。通过模型与推导方法总结提出有效预测盾构开挖上方地表纵向变形的普适性理论公式，并以实际工程对公式进行验证，为超大直径盾构施工引起的地表变形控制提供参考。

1 研究区域概况

1.1 北横工程现场地质条件

上海市北横工程场地90 m以内分布的土层自上而下可划分为9大层及若干亚层和透镜体夹层，其中①层为填土，②1层～⑤3层为全新世Q4沉积层，⑥层～⑨层为上更新世Q3沉积层。工程沿线穿越的河流主要为吴淞江，受黄浦江潮位影响较为明显，河道周边地层的②3层粉砂渗透性较好，是地表水和地下水良好的联络通道。勘察发现沿线地下水主要是存储于浅部土层中的潜水，分别是：赋存于⑤1T、⑤2层中的微承压水，赋存于⑦层、⑨层中的承压水。根据上海地区的工程实践，本场地环境类型按Ⅲ类考虑。地质剖面及水文条件如图2所示。

1.2 北横通道隧道地表变形实测分析

北横通道范围为威宁路接地点（K1+570.73）～长安路接地点（K9+359.50），全长7 788.77 m。主线盾构隧道段以中山公园工作井划分为东西两段，西线为中江路工作井至中山公园工作井，东线为中山公园工作井至筛网厂工作井。圆形隧道外径为15 m，管片厚度600 mm，中心环宽2.0 m。西线盾构段全长2 751 m，最低标高达到-44.73 m，目前东西线即将全线贯通。

西线隧道大部分区段在苏州河下方开挖，地表变形情况难以监测，而靠近两端工作井隧道埋深变化较大，地表监测数据也无法反映清晰规律。因此选取了地表变形规律、土层厚度变化少的盾构切口位于第388环、第391环、第409环、第412环4个时间节点测得的地表变形数据进行分析。对应环号上方地表沉降曲线如图3所示。

通过对北横超大直径隧道工程现场实测数据图3分析可以发现，超大直径盾构掘进引起地表变形影响范围较大，影响地面变形范围长达120 m。即距离刀盘前方60 m开始隆起，到距离刀盘前方10～20 m为隆沉临界点，然后开始沉降，直至到达刀盘后方50～60 m沉降达到基本稳定。因此超大直径盾构隧道掘进过程对地表变形分析尤为重要。对比图1以及上述工程现场实测数据图3来看，地表变形曲线在Ⅰ、Ⅱ阶段与抛物线拟合度较高，Ⅲ阶段变形曲线与直线拟合度较高，在Ⅳ阶段由于沉降最终会趋于稳定，因此将Ⅳ阶段变形曲线拟合成双曲线。通过调研可知虹梅路越江隧道等其他大直径盾构隧道地表纵向沉降曲线也有此规律。

2 盾构刀盘前方地表变形特征数值分析

2.1 刀盘前方地表变形机理

盾构刀盘前方地表变形主要通过支护压力进行控制。在施工过程中，盾构机通过刀盘旋转切削前方土体实现开挖掘进。对于常见的土压平衡盾构，为了保证刀盘前方土体的稳定性，盾构机主要通过刀盘向开挖面施加支护压力，与前方土压力进行平衡，以控制土层位移乃至地表变形。地表变形主要包括沉降与隆起两种形式：当刀盘支护压力小于前方土压力时，土体向刀盘方向移动，达到极限平衡状态后出现主动破坏，破坏发展至地表而表现为沉降;当刀盘支护压力大于前方土压力时，土体受到刀盘挤压作用逐渐增大，达到极限平衡状态后出现被动破坏，破坏发展至地表而表现为隆起。

2.2 有限元模型建立

为研究不同支护压力作用下刀盘前方地表隆起规律，采用Midas GTS NX 2018软件，参考北横通道新建工程Ⅱ标段工程实践及现场地勘报告，建立三维有限元模型如图4所示。模型中盾构机钢壳参考钢材参数采用弹性本构建立，土体采用摩尔-库伦本构建立，具体计算参数如表1所列。模型底面设置竖向及水平位移约束，侧面设置法向位移约束，顶面不设置约束。

2.3 有限元模拟方案

本次模拟不考虑衬砌管片，开挖土体后生成盾构机钢壳，不针对盾构类型分类，将支护形式简化为仅在开挖面上施加支护压力。通过调整支护压力的大小，研究不同覆土厚度情况下刀盘前方土体的变形规律。模拟方案中以比值的形式对覆土厚度与支护压力进行取值，即以埋深比（覆土厚度C/盾构刀盘直径D）考虑覆土厚度，以支护比（支护压力σ/初始地层压力σ0）考虑支护压力。

考虑到实际工程中大直径盾构支护压力随深度变化，特别是对于超过14 m级超大直径盾构，刀盘顶部与底部压力差较大，为了更真实地还原支护状态，该模型中支护压力均采用上小下大梯形分布，如图5所示。其量值与开挖面前方同埋深段土压力呈倍数关系。据此，本次数值模拟在常规覆土厚度范围内设定了3种埋深比（C/D），分别为1.0，1.5，2.0;在初始静止状态与被动极限状态之间设定了5种支护比（σ/σ0），分别为1.0，1.5，2.0，2.5，3.2。当σ/σ0>3.2，有限元模型计算出现不收敛，因此认为当σ/σ0=3.2时土体处于被动极限状态。

2.4 模拟结果分析

2.4.1 被动极限状态下地表隆起规律

图6为不同埋深比情况下，土体达到被动极限状态时（σ/σ0=3.2）刀盘前方的地表变形曲线。可以看出：当σ/σ0=3.2时，刀盘前方部分地表表现为隆起，且不同埋深比情况下地表隆起程度有所不同;随着埋深比的增加，刀盘前方的地表最大隆起值有所减小，且最大隆起位置逐渐远离刀盘。虽然不同埋深比的地表隆起情况存在差异，但最大隆起值均在10 mm上下浮动，且刀盘前方的部分地表隆起形状基本一致。利用二次抛物线对隆起部分的地表变形数据进行拟合，拟合度因子R2均达到0.99以上，可以认为该部分地表隆起形状基本表现为二次抛物线形式。

2.4.2 埋深比与支护比对地表隆起的影响

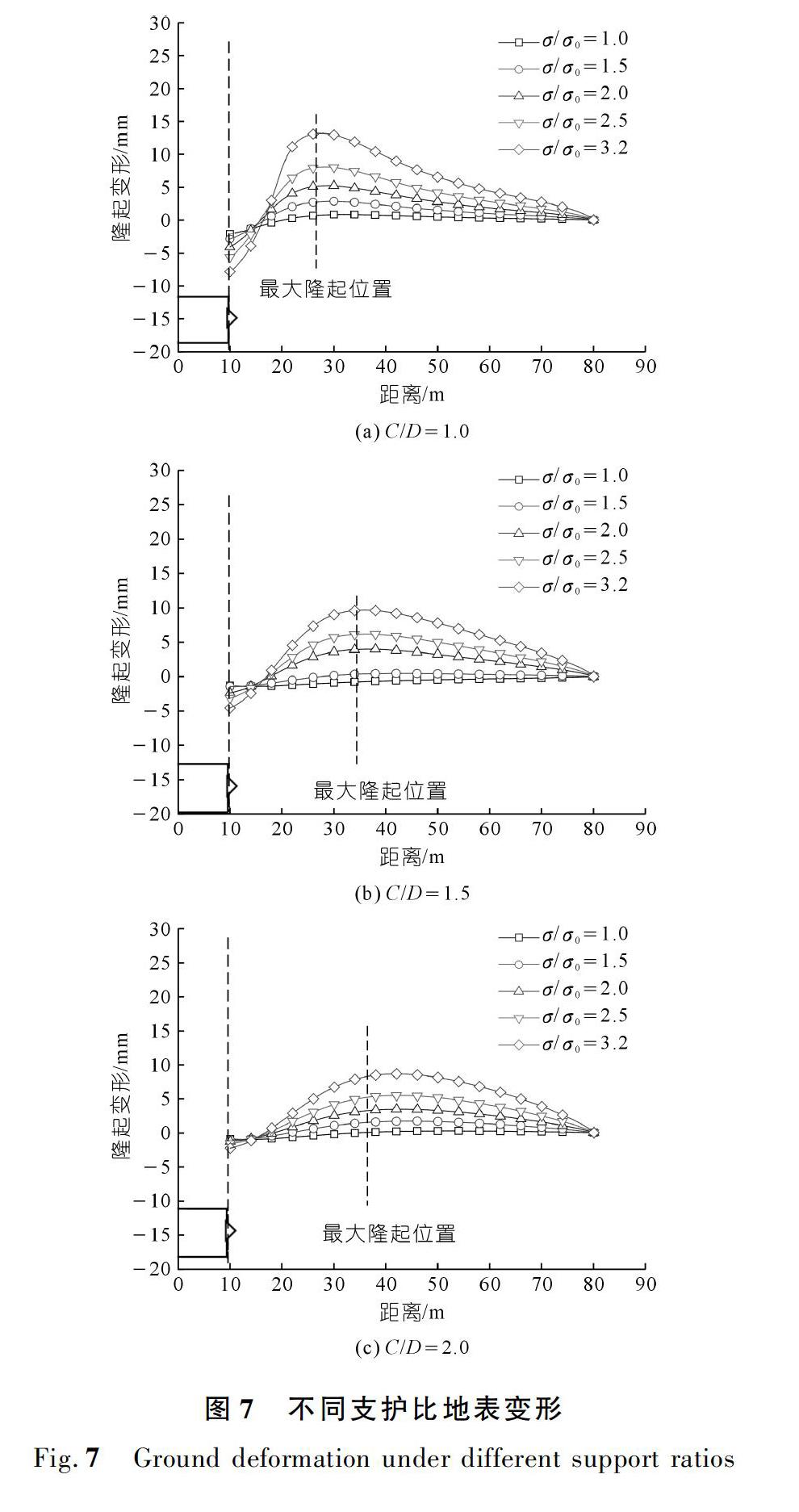
本次模拟在初始静止状态与被动破坏状态之间设置了5种支护比，分别施加在开挖面上，以研究不同支护压力对刀盘前方地表隆起的影响，所得地表隆起变化如图7所示。

由图7可知：同一埋深比情况下，随着支护比增大，刀盘前方地表最大隆起值逐渐增大，但最大隆起位置基本不变;同一支护比情况下，随着埋深比的增大，刀盘前方地表最大隆起值逐渐减小，且最大隆起位置向刀盘前方移动，即隆起范围逐渐远离刀盘。因此，可以认为最大隆起值与支护压力有关，而隆起范围则与覆土厚度有关。

图8为不同埋深比情况下，刀盘前方地表最大隆起值随支护比的变化规律。可以看出，随着支护比的增大，最大隆起值逐渐增大。图9为不同支护比作用下，最大隆起点与刀盘水平距离随埋深比的变化规律。

可以看出，随着埋深比的增大，最大隆起点与刀盘水平距离增大，即最大隆起点逐渐远离刀盘。因此，可以认为支护压力越大，地表隆起程度越大;覆土厚度越大，地表隆起范围距离刀盘越远。

3 超大直径盾构地表变形分析模型

根据前述变形阶段划分原理，提出超大直径盾构施工引起的纵向地表变形计算模型如图10所示。

其中横坐标为地表某点与刀盘的水平距离，纵坐标为地表变形量（正值为隆起，负值为沉降）。预测范围设定为切口压力影响范围至地表沉降稳定基本之间。主要将盾构施工引起的地表纵向变形发展分为 4 个阶段。

图10中横坐标为地表某点与刀盘的水平距离，纵坐标为地表变形量（正值为隆起，负值为沉降）。预测范围设定为切口压力影响范围至地表沉降稳定基本之间。

3.1 I阶段，AB抛物线段（a2≤x≤a1）

根据第2节对有限元模拟结果的分析，认为刀盘前方地表的隆起程度及隆起范围分别与施工参数中的支护压力及覆土厚度存在一定关系，针对这2个主要施工参数，根据图10中A、B两点位置坐标关系，提出刀盘前方地表隆起的理论分析模型计算公式为

式中：S（x）为地表隆起量，mm;x为地表某点与刀盘水平距离，m;Smax为当前支护压力作用下地表最大隆起值;a2为最大隆起点B处与刀盘距离，a1为隆起零点A处距离，计算公式分别为

式中：σ为开挖面支护压力，σ0为静止土压力，σp为被动土压力，Smax0为被动极限情况对应的地表最大隆起值，根据实际支护压力对Smax0进行内插可得Smax，即当σ=σp时，Smax=Smax0，當σ=σ0时，Smax=0。

静止土压力：

式中：C为隧道覆土厚度;D为盾构刀盘直径;q为地表堆积荷载，一般取值为零。其中K0=1-sinφ，φ为内摩擦角。

式中：α为隆起扩散角，表示刀盘前方土体受到挤压后向地表发展的路径方向，在被动破坏土体受挤压状态下一般取值为45°～ 45°+φ/2，当达到极限破坏时最大45°+φ/2。同时，考虑到不同覆土厚度对土体位移发展路径的影响，在隆起范围的计算中引入埋深修正系数ηd，根据埋深比在1.0～1.2之间取值，埋深比越大，ηd越大。

3.2 Ⅱ阶段，BC抛物线段（a3≤x≤a2）

式中：a3为隆沉分界点C点距离，引入比例系数k=a1-a2a2-a3，工程现场统计数据k在1～3取值，其他参数意义同前。

3.3 Ⅲ阶段，CM直线段（0≤x≤a3）

式中：β1为刀盘盾尾直径差沉降影响系数;D为盾构刀盘直径，m;DT1为盾尾直径，m。

3.4 IV阶段，MN双曲线段（x≤0）

式中：双曲线常数a、b均为待定系数。

由式（10）和（12）可得：

根据公式（1）～（11），只要知道支护压力σ、隧道埋深C、盾尾直径DT1、盾构刀盘直径D以及相关土体参数，刀盘盾尾直径差沉降影响系数β1，双曲线常数b，即可得出当前工况下盾构上方地表的纵向变形曲线。

如果随着隧道的掘进，地质条件发生变化时，参数重度γ、凝聚力c、内摩擦角φ等一系列地层参数都会改变，将改变后的参数代入公式（1）～（11），计算出新的数值。

4 工程验证

为验证盾构上方地表纵向变形理论公式的准确性与实用性，以下选取北横通道西线中第409环作为算例，并与盾构开挖至这一环时所监测得到的地表变形数据进行对比。图11为北横通道布置图。

参考JGJ 120-2012《建筑基坑支护技术规程》中关于基底附加荷载扩散角的规定，以45°考虑盾构隧道塑性区的扩散，因此将刀盘支护压力产生的挤压隆起扩散角α，取为45°。根据有限元模型分析及现场监测所得规律，将被动破坏状态对应地表最大隆起量Smax0取为10 mm。

根据工程地勘报告所得第409环所在区域，覆土厚度C=29.19 m，盾构刀盘直径D=15.56 m，盾尾直径DT1=15.47 m，支护压力σ=480 kPa;埋深比为2.01，取埋深修正系数ηd=1.2;取比例系数k=2.0;土体参数取其上部各层土加权平均值，重度γ=18.53 kN/m3，凝聚力c=7.33 kPa，内摩擦角φ=26.4°。

根据公式（1）～（11）及以上参数可计算得利：K0=0.58，σ0=399 kPa，Kp=2.46，σp=1 744 kPa，最大隆起点位置a2=35.03 m，起始隆起点位置a1=52.43 m，隆沉分界点位置a3=26.33 m，当前支护压力对应最大隆起值Smax=0.60 mm。其中刀盘盾尾直径差沉降影响系数β1，双曲线常数b，均为待定。通过拟合取β1=0.039，b=0.03，根据式（12）得a=7.478。所计算结果与实测数据对比如图12所示。

可以看出，理论模型的计算结果与实测数据相比，变形程度、变形范围与变形形式均较为吻合，可以认为该理论分析模型能够较好地预测盾构掘进中地表纵向变形。

5 结 论

（1） 通过工程现场实测数据，分析地表纵向变形曲线在Ⅰ、Ⅱ阶段呈抛物线趋势变化，Ⅲ阶段呈直线趋势变化，在Ⅳ阶段呈双曲线趋势变化。

（2） 当土体达到被动极限状态时，刀盘前方地表均表现为隆起，且被动极限状态时最大隆起值约为10 mm。实际盾构掘进过程中，如果达到极限破坏状态下盾构开挖面将出现很大的破坏倒塌，因此当地表隆起值接近10 mm时应注意改变施工参数，不能让其达到极限状态，否则会出现工程事故。

（3） 同一埋深比情况下，随着支护比增大，刀盘前方最大隆起值逐渐增大，但最大隆起位置基本不变;同一支护比情况下，随着埋深比的增大，最大隆起点与刀盘水平距离增大，即隆起范围逐渐远离刀盘，但刀盘前方最大隆起值逐渐减小。

（4） 本文理论模型的计算结果与实测数据相比，地表变形程度、变形范围与变形形式均较为吻合，认为该理论模型能够较好地预测盾构掘进地表纵向变形。

参考文献：

[1] 王建秀，田普卓，付慧仙，等.基于地层损失的盾构隧道地面沉降控制[J].地下空间与工程学报，2012，8（3）：569-576.

[2] 郑宜枫，丁志诚，戴仕敏.超大直径盾构推进引起周围土体变形和土水压力变化分析[J].地下空间与工程学报，2006，2（8）：1349-1378.

[3] 王建秀，邹宝平，付慧仙，等.超大直径盾构下穿保护建筑群地面沉降预测[J].现代隧道技术，2013，50（5）：98-104.

[4] 林存刚，刘干斌，吴世明，等.泥水盾构掘进引起的地面沉降：传统计算理论的评析与修正[J].土木工程学报，2015，48（4）：111-123.

[5] 林存刚，吴世明，张忠苗，等.泥水盾构隧道施工引起的地面沉降分析及预测[J].土木建筑与环境工程，2012，34（5）：26-32.

[6] 林存刚，张忠苗，吴世明，等.泥水盾构掘进参数对地面沉降影响实例研究[J].土木工程学报，2012，45（4）：116-126.

[7] 梁荣柱，夏唐代，林存刚，等.盾构推进引起地表变形及深层土体水平位移分析[J].岩石力学与工程学报，2015，34（3）：583-593.

[8] 周顺华.地铁盾构法隧道下穿工程[M].北京：科学出版社，2017：170-175.

[9] 林存刚，吴世明，张忠苗，等.盾构掘进速度及非正常停机对地面沉降的影响[J].岩土力学，2012，33（8）：2472-2482.

[10] 刘波，杨偉红，张功，等.基于隧道不均匀变形的地表沉降随机介质理论预测模型[J].岩石力学与工程学报，2018，37（8）：1943-1952.

[11] SEUNG H K，FULVIO T.Face stability and required support pressure for TBM driven tunnels with ideal face membrane-drained case[J].Tunnelling and Underground Space Technology，2010（25）：526-542.

[12] 張忠苗，林存刚，吴世明，等.泥水盾构施工引起的地面固结沉降实例研究[J].浙江大学学报（工学版），2012，46（3）：432-440.

[13] ZHANG Z X，HU X Y，KIEFFER D S.A discrete numerical approach for modeling face stability in slurry shield tunnelling in soft soils[J].Computers and Geotechnics，2011（38）：94-104.

[14] 林存刚，张忠苗，吴世明，等.软土地层盾构隧道施工引起的地面隆陷研究[J].岩石力学与工程学报，2011，30（12）：2584-2592.

[15] 魏纲，张金菊，魏新江.数学模型在盾构地面长期沉降预测中的应用[J].地下空间与工程学报，2009，5（3）：541-545.

（编辑：郑 毅）

引用本文：

方小明，张孟喜，张梓升，等.超大直径盾构掘进引起地表纵向变形规律分析

[J].人民长江，2021，52（7）：160-167.

Analysis on longitudinal deformation of ground surface caused by excavation

of super large diameter shield

FANG Xiaoming1，ZHANG Mengxi1，ZHANG Zisheng1，XIAO Xiaochun2，LI Lei2

（1.Department of Civil Engineering，Shanghai University，Shanghai 200444，China; 2.Shanghai Tunnel Engineering Co.，Ltd.，Shanghai 200032，China）

Abstract：

To establish a theoretical analysis model of surface deformation caused by shield tunneling，based on the statistical analysis of the measured data of longitudinal surface deformation of the Beiheng super large diameter shield tunnel in Shanghai City，the finite element software is used to simulate the construction of shield tunnel，and the relationship between the surface deformation in front of cutter head and construction parameters is mainly studied.The results show that when the soil reaches the passive limit state，the maximum uplift value in front of the cutter head is about 10 mm，the uplift form is approximately quadratic parabola;under the same buried depth ratio，the maximum uplift value in front of cutter head is directly proportional to the support ratio;under the same support ratio，with the increase of buried depth ratio，the uplift range gradually moves away from the cutter head and moves forward，and the change relationship between them is proportional.This indicates that the degree and range of surface uplift in front of cutter head are related to support pressure and overburden thickness.Based on the analysis of the results of finite element simulation and mathematical derivation，a theoretical model for predicting the surface longitudinal deformation caused by shield tunneling is proposed.The engineering example shows that the prediction results of the theoretical model are in good agreement with the field measured data of the Beiheng cross passage.The theoretical model has important reference value for other similar projects.

Key words：

ground surface deformation;shield tunnel;shield excavation;finite elementanalysis