基于半监督信息的截集式可能性C-均值聚类算法

范九伦 高梦飞于海燕 陈斌斌

(西安邮电大学通信与信息工程学院 西安 710121)

(西安邮电大学电子信息勘验应用技术公安部重点实验室 西安 710121)

1 引言

图像分割[1]是计算机视觉领域中的重要技术，是后续进行图像分析与识别的基础，其目的是从图像中将感兴趣的区域与其他部分进行分离并提取出来。常规的图像分割方法包括：基于阈值的分割方法[2]、基于区域的分割方法[3]、基于边缘的分割方法[4]、基于聚类的分割方法[5]等。作为聚类图像分割的常用方法，模糊C-均值(Fuzzy C-Means,FCM)[6]对噪声点和奇异点非常敏感。这主要是缘于该算法对隶属度有约束条件：要求各个样本点到所有类的隶属度之和必须为1。

为解决FCM聚类算法对噪声敏感的问题，Krishnapuram等人[7]提出可能性C-均值(Possibilistic C-Means,PCM)聚类算法，PCM聚类算法放弃了FCM聚类算法中隶属度和为1的约束条件，能明显改善FCM聚类算法的噪声敏感问题。然而PCM聚类算法完全释放了类间关系，只有PCM目标函数在全体聚类中心重合时才能获得真正的全局最优解，导致PCM聚类算法非常不稳定，容易出现聚类中心重合的问题[8,9]。除此之外，PCM聚类算法还存在对初始化敏感、参数设置敏感等一系列问题。为解决这些问题，学者对PCM聚类算法进行了一些改进，Pal等人[10]提出了可能性-模糊混合聚类算法，以克服聚类中心重合现象。Memon等人[11]将核PCM聚类算法和FCM聚类算法相结合，提出了结合局部信息的核PCM聚类算法，该算法提高了PCM对噪声的鲁棒性。

针对PCM的聚类中心重合问题，从隶属度的修改入手，文献[12]提出了截集式可能性C-均值(Cutset-type Possibilistic C-Means,C-PCM)聚类算法，C-PCM聚类算法将截集门限引入PCM聚类算法中，并选择部分样本的隶属度进行修改，从而引入类间关系，该算法在一定程度上能够克服PCM的聚类中心重合问题。C-PCM聚类算法在对目标大小相近的数据聚类的时候，能够找到正确的聚类中心，但是对小目标数据进行聚类时仍然存在聚类中心重合问题。具体来说，小目标的聚类中心会严重偏离到大目标的数据区域，从而影响聚类效果。

半监督聚类[13–15]使用半监督信息来指导聚类过程，一定程度上改善了聚类效果和运行效率。2009年，Yasunori等人[13]将监督隶属度引入FCM聚类算法中，提出了半监督模糊C-均值(Semi-Supervised Fuzzy C-Means,SS-FCM)聚类算法。2012年，Yin等人[14]提出将监督隶属度引入熵正则化FCM聚类算法中，提出了熵正则化半监督模糊聚类算法，避免了模糊因子人为确定的问题。本文将半监督引入C-PCM聚类算法中，提出半监督截集式可能性C-均值(Semi-Supervised Cutset-type Possibilistic C-Means,SS-C-PCM)聚类算法，通过将标签数据引入目标函数中，防止C-PCM聚类算法的中心偏移问题，从而改善了小目标数据的聚类效果。

超像素最早由Ren等人[16]提出，它由一系列位置相邻且颜色、亮度、纹理等特征相似的像素点组成子区域，这些子区域保留了进一步进行图像分割的有效信息，并且不会破坏图像中物体的边界信息。同时超像素图像的子区域内的像素具有相近的图像特征，针对小区域进行处理可以大大减少计算量，提高分割效率[17–20]。鉴于此，本文将超像素子区域信息以彩色直方图[21]的形式引入SS-C-PCM聚类算法的目标函数中，进一步提出了一种基于差分进化超像素的半监督截集式可能性C-均值

(differential evolutionary superpixel-based Semi-Supervised Cutset-type Possibilistic C-Means,desSS-C-PCM)聚类算法，提高了聚类算法的运行效率。

2 可能性C-均值聚类算法

为了改善FCM聚类算法的噪声敏感性，Krishnapuram等人[7]提出了PCM聚类算法，该算法通过改变FCM聚类算法的约束条件进而减少噪声对聚类的影响。PCM算法的目标函数为

PCM聚类算法通过释放隶属度和为1的约束条件，提高了聚类算法对噪声的鲁棒性。但是PCM对隶属度的约束过于宽泛，使得PCM缺乏类间关系，目标函数(式(1))在全体聚类中心重合时才能获得真正的全局最优解，最终导致算法容易产生聚类中心重合问题[8,9]，也称为一致性聚类问题。此外PCM聚类算法存在对初始化、参数设置敏感的问题。

3 截集式可能性C-均值聚类算法

为了克服PCM最突出的问题—中心重合问题，Yu等人[12]将截集概念引入PCM聚类算法中，通过截集门限选择部分样本点并修改其典型值，进而引入类间关系，从而提出了截集式可能性C-均值(C-PCM)聚类算法，能够在一定程度上克服PCM的聚类中心重合问题。C-PCM的目标函数为

典型值t k i和聚类中心vk的更新公式与PCM算法的更新公式相同，惩罚因子η为提前设置，在算法中取固定值。其中，截集采用基于阴影集的理论[22,23]自适应选取。C-PCM聚类算法通过将样本点的非获胜典型值进行修改，进而增大获胜典型值与非获胜典型值的差值，从而引入类间关系。该算法在对各类大小相近的数据进行聚类时，能够很好地克服PCM的聚类中心重合问题。但是在各类样本容量大小相差较大，即包含小目标的数据进行聚类时，仍然存在聚类中心偏移、部分中心重合问题。

4 半监督模糊C-均值聚类

当样本不平衡时，C-PCM算法对包含小目标的数据进行聚类时，存在聚类效果不理想的问题。具体来说如果数据集中存在一个类的样本容量很大，而另一类的样本容量很小，那么样本容量较小的类中心很容易就偏移到样本容量大的数据区域中。针对这一问题，本文借鉴Yasunori等人[13]提出的半监督思想，将监督隶属度引入C-PCM聚类算法中。Yasunori等人[13]提出半监督模糊C-均值(Semi-Supervised Fuzzy C-Means,SS-FCM)聚类算法，其目标函数为

5 本文算法

SS-FCM聚类算法利用已知类别标签的少量样本指导模糊聚类过程，一定程度上提高了运行效率。本文引入该算法的思想，将监督信息融入CPCM聚类算法的目标函数中，提出半监督截集式可能性C-均值(Semi-Supervised Cutset-type Possibilistic C-Means,SS-C-PCM)聚类算法；同时将SS-C-PCM聚类算法应用到彩色图像中：为了降低计算复杂度，提高分割效果，利用差分进化超像素算法对图像进行预处理的同时引入空间信息，进而提出了一种基于差分进化超像素的半监督截集式可能性C-均值聚类算法desSS-C-PCM。

5.1 半监督截集式可能性C-均值聚类算法

针对C-PCM聚类算法对包含小目标的数据进行聚类时出现中心偏移、部分中心重合现象，本文借鉴半监督模糊C-均值聚类算法[13]的思想，将半监督信息引入C-PCM的目标函数中，利用已知类别标签的少量样本指导C-PCM聚类算法的聚类过程。半监督截集式可能性C-均值聚类算法的目标函数为

5.2 基于差分进化超像素的半监督截集式可能性C-均值聚类算法

传统的聚类图像分割算法是在像素层面进行聚类，其计算复杂度高，算法运行时间长，占用空间大。超像素图像是一系列位置相邻且颜色、亮度、纹理等特征相似的像素点组成的子区域，且超像素子区域的个数远小于彩色图像的像素数。差分进化超像素(Differential Evolutionary Superpixel,DES)算法是由Gong等人[19]在2018年提出的一种新的基于全局优化的进化超像素方法，相对于简单线性迭代聚类超像素算法[20]，该算法可以更好地捕获图像的边界信息，提高图像的边界依附性。为减少计算量，改善图像的分割效果，本文将差分进化超像素(DES)算法获取的超像素子区域信息引入本文的SS-C-PCM图像分割算法中，并借鉴Lei等人[21]提出的彩色直方图的方法重新设计目标函数，进而提出了一种基于差分进化超像素的半监督截集式可能性C-均值(differential evolutionary superpixel-based Semi-Supervised Cutset-type Possibilistic C-Means，desSS-C-PCM)聚类算法，该算法的目标函数为

基于差分进化超像素的半监督截集式可能性C-均值(desSS-C-PCM)聚类算法步骤如下，流程图如图1所示。

图1 desSS-C-PCM算法流程图

步骤1给定聚类数目c，超像素个数k，模糊因子m，惩罚因子η。设置最大循环次数Tmax和算法停止的阈值ε；

6 实验结果分析

为了验证本文所提SS-C-PCM和d esSS-CPCM算法有效性，本节采用人工合成数据集和Berkeley图像[24]进行仿真实验，采用的对比算法有FCM聚类算法、SS-FCM聚类算法、C-PCM聚类算法。实验环境为MATLAB R2014a，参数设置分别为m=2，设置η为 20，最大迭代次数rmax=100，算法停止的阈值为ε=0.00001。

6.1 人工合成数据实验

图2显示了各个算法对3类数据集的聚类结果，可以看出FCM,SS-FCM,C-PCM算法其中一类的中心发生严重偏移，而本文所提SS-C-PCM算法利用少量的监督信息来指导聚类过程，得到的中心只发生了轻微偏移。表1显示了各个算法的中心偏移量。

表1 针对数据集X1600各个算法的中心偏移量以及迭代次数

图2 针对数据集X 1600的聚类结果

6.2 Berkeley图像对比实验

对于图3#124084，其标准分割应为3类：红色花瓣为第1类，黄色花蕊为第2类，除花以外的背景归为第3类。FCM算法在背景处理上出现了较多的错分；C-PCM算法将花瓣和花蕊分割为一类，没有成功地分割出花蕊，分割效果较差；SS-FCM算法虽然在FCM的基础上加入了半监督，提高了该算法的运行效率，但是分割结果相对于FCM，并没有得到提升；SS-C-PCM算法相对于C-PCM算法，分割效果有一定的改善；desSS-C-PCM算法虽然在一些细节上出现了分割错误，但是能较好地将花朵从背景中分割出来。

图3 #124084分割结果图

表2分别给出了FCM,C-PCM,SS-FCM,SSC-PCM算法以及desSS-C-PCM算法的分割准确率，从表2可以看出，FCM算法和C-PCM算法的分割准确率相对较低；SS-FCM算法在分割图像#3063,#135069以及#238011时，分割准确率相对于FCM有比较明显的提升，对于大部分图像，SSFCM的分割准确率相对于FCM没有明显的改善；SS-C-PCM算法在C-PCM算法的基础上加入了半监督，相对于C-PCM算法，SS-C-PCM算法在分割图像#42044时，分割准确率下降了0.0114，在分割其余18张图像时，SS-C-PCM算法的分割准确率都有所提高；desSS-C-PCM算法通过DES超像素获取空间信息，并通过半监督信息来指导聚类过程，所以分割准确率有明显的提高。

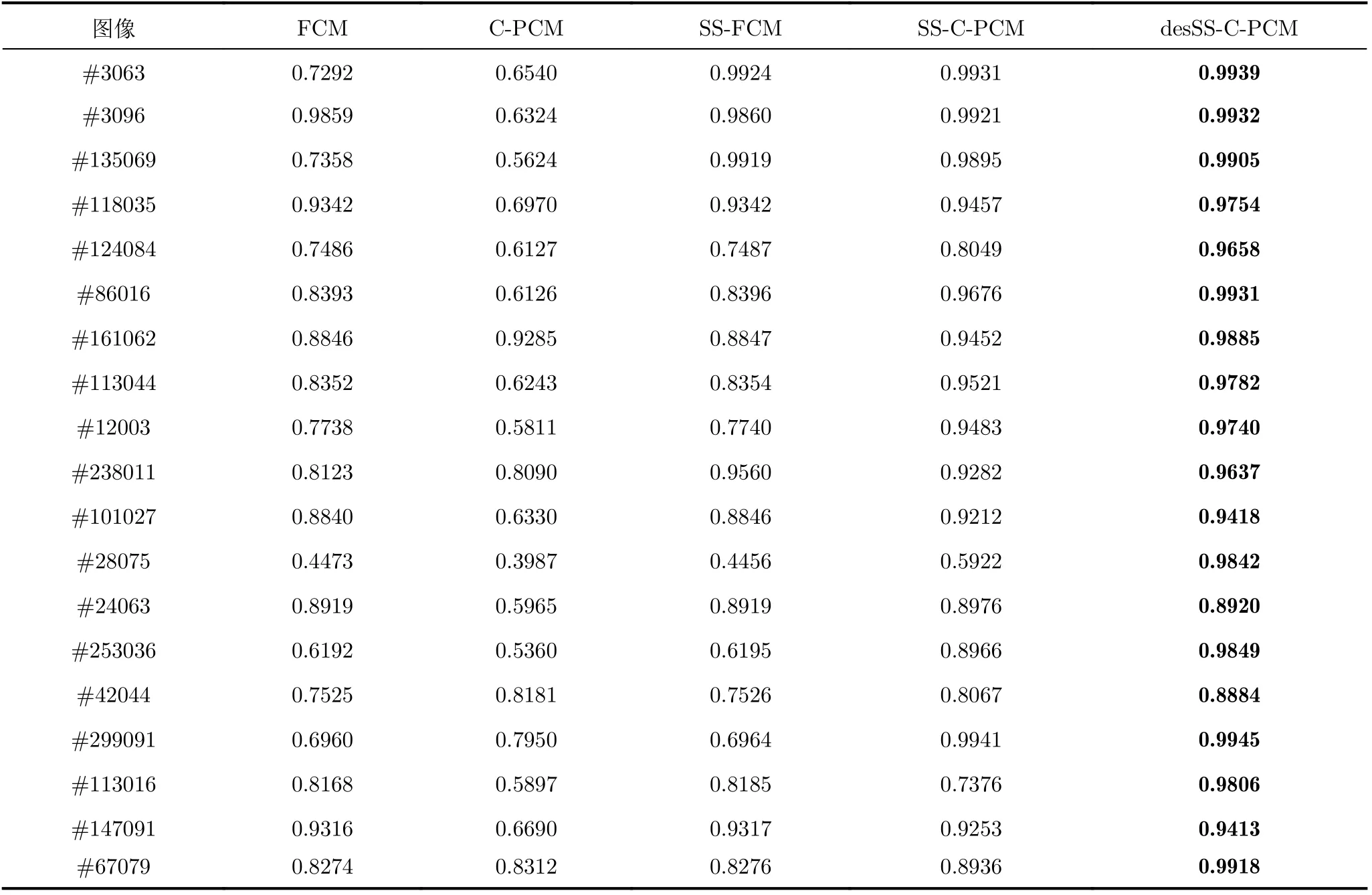
表2 各个算法的分割准确率对比

7 结束语

针对C-PCM算法在处理小目标数据时聚类中心严重偏移的问题，本文将半监督信息引入C-PCM算法，提出半监督截集式可能性C-均值(SS-CPCM)聚类算法。为了改善C-PCM算法对彩色图像的分割效果以及运行效率，本文通过DES超像素算法获取空间信息，将此空间信息引入SS-C-PCM算法中，提出基于DES超像素的半监督截集式可能性C均值(desSS-C-PCM)聚类算法，并将其用到彩色图像分割。实验结果表明，SS-C-PCM算法提高了C-PCM算法的运行效率以及分割准确率，desSSC-PCM算法在SS-C-PCM算法的基础上进一步提高了分割准确率以及运行效率。下一步将研究本文算法在噪声环境下对彩色图像的分割效果。