网络弹性与恢复机制的研究综述

刘青霞,王 邦

1华中科技大学电子信息与通信学院 武汉 中国 430074

1 引言

现实世界的系统和网络并不总是稳定。2003年8月 14日,美国东北部以及加拿大东部地区出现的严重停电事故,就是因为少量输电线路的故障破坏了电网稳定性,最终导致大范围的电网崩溃[1]。2017年5月12日,全球范围爆发的Wannacry病毒勒索事件,源于病毒利用微软操作系统漏洞进行大规模传播,从而导致超过 20万台电脑主机遭受到攻击[2]。计算机网络、通信网络,以及交通系统、电力系统等具有网络化结构的基础设施等,在内部故障或外部攻击下处于低效率的工作状态甚至完全崩溃,对社会的运转和人们的生活有着巨大影响。

研究者们基于复杂网络理论对网络失效机制进行了深入研究[3]。随机故障或蓄意攻击造成一些网元失效(即节点、连边失效),而失效的网元会影响其相邻网元的工作状态,并引发更多网元失效,即失效在网络中传播,形成网络的级联失效过程。网元失效使得网络的连通度降低,而当失效网元数量达到一定比例时,网络的拓扑结构突然崩溃,不再存在较大尺度的巨连通集团,网络功能不再能满足网络的基本运行要求,这也称之为网络的渗流相变。从攻击的角度,大量的研究建模了网络的级联失效过程和渗流相变现象[4-7],也提出了多种攻击策略,目的是为了高效破坏网络,加快崩溃进程,如: 基于节点中心性的攻击[8]、基于关节节点的攻击[9]、基于节点集体影响力的攻击[10]、基于节点集合的攻击[11-12]等。

另一方面,网络恢复机制主要研究网络失效后应采取何种策略治愈失效网元,从而尽快恢复网络的正常功能,这对于保护重要网络和基础设施的正常运行具有极为重要的意义。研究者们提出网络弹性的概念,用以描述网元失效时的网络防护和恢复能力。针对不同的网络类型和失效机制,近年来一些研究提出了不同的网络恢复策略用以增强网络弹性。本文重点关注在网络失效过程中的网络应急恢复机制。首先介绍网络弹性的概念,接着梳理了最近几年网络恢复机制的相关研究,并以基础设施网络举例说明网络恢复策略的应用,最后对未来研究发展方向进行了展望。

2 网络弹性

2.1 相关概念

弹性通用于表示实体或系统承受、适应破坏,并从中恢复的能力[13]。本文探讨的网络弹性主要是指当网络出现级联失效时,网络维持或恢复原有功能的能力(性能可能有所降低)。例如,基础设施安全合作协会[14]这样定义具有弹性的基础设施网络: 网络能预防、应对或缓解任何预期或意料之外的重大安全事件,并能以最小的损失迅速恢复并重新配置关键资源和服务。

网络弹性主要体现在两个方面: 在网元失效后,控制网络级联失效规模的防护能力,以及在发生级联失效时,网络的快速恢复能力。网元失效的原因很多,大体上可以分为三种,即随机故障、蓄意攻击和局部破坏。随机故障往往表现为网络中节点或连边的内部故障,具有自发性、不确定性。蓄意攻击则是外部为破坏网络功能而利用某种策略选择性攻击特别的节点或连边。随机故障和蓄意攻击针对全局网络而言,失效网元分布在整个网络。局部破坏则体现在使得某一特定地理区域内子网络的所有节点和连边聚集性失效,例如现实中自然灾害(如地震等)或大规模攻击(如轰炸等)而造成某一地区的网络失效。

少量网元失效可能引发大规模的网络级联失效,甚至造成网络崩溃。在网元失效后,网络的防护机制通过实施预设的防护策略来减缓网络的失效过程,阻止大规模级联失效甚至网络崩溃的产生。网络的防护主要通过预测脆弱的、可能失效的网元,针对性地进行重点保护或资源调控来实现。针对不同的网络类型和运行模式,近些年提出了许多防护策略。一些防护策略依据中心性指标来选择网络中的重要节点进行特别保护,通过防止这些节点在攻击下失效来实现对级联失效规模的控制[15-16]。Wang等[17]根据节点负荷分布来选择一些特定的节点进行保护,减少这些节点过载时的负荷,使其不易失效,维持正常工作状态。一些预防机制通过设置一些备份连边,平时不启用,而只有在网络结构遭到破坏时才启用来替代失效连边,从而维持网络的连通性和功能[18-20]。一些预防机制则从网络结构出发,对于具有耦合机制的相依网络,通过改变不同网络间的依赖程度和相依连边的类型等来增强抵御攻击的能力[21-25]。特别地,Motter[26]提出一种预防性移除的防护策略。当出现失效网元时,提前移除一些正常节点,阻止失效节点将原来所承载的网络负荷传导到更多节点,从而预防更大规模的网络级联失效。

网络发生失效后,网络的恢复机制通过治愈失效网元或增加新网元等方式恢复网络的部分或完整功能。本文关注网元失效引发级联失效时,采用何种策略使得能尽可能短的时间内应急恢复网络结构和功能。网络恢复机制近几年得到了重视和研究,主要的恢复策略可以分为两种类型: 自发性恢复(spontaneous recovery)和指向性恢复(targeted recovery)。自发性恢复主要指的是级联失效发生时,网络中受损的部分自发地恢复功能的过程。指向性恢复是指当网络无法自动恢复功能或在一定时间内无法复原时,外部合理分配资源对网络中严重受损的部分进行恢复的过程。相关文献总结如表1所示。下一章将分别从这两个方面介绍网络的恢复机制。

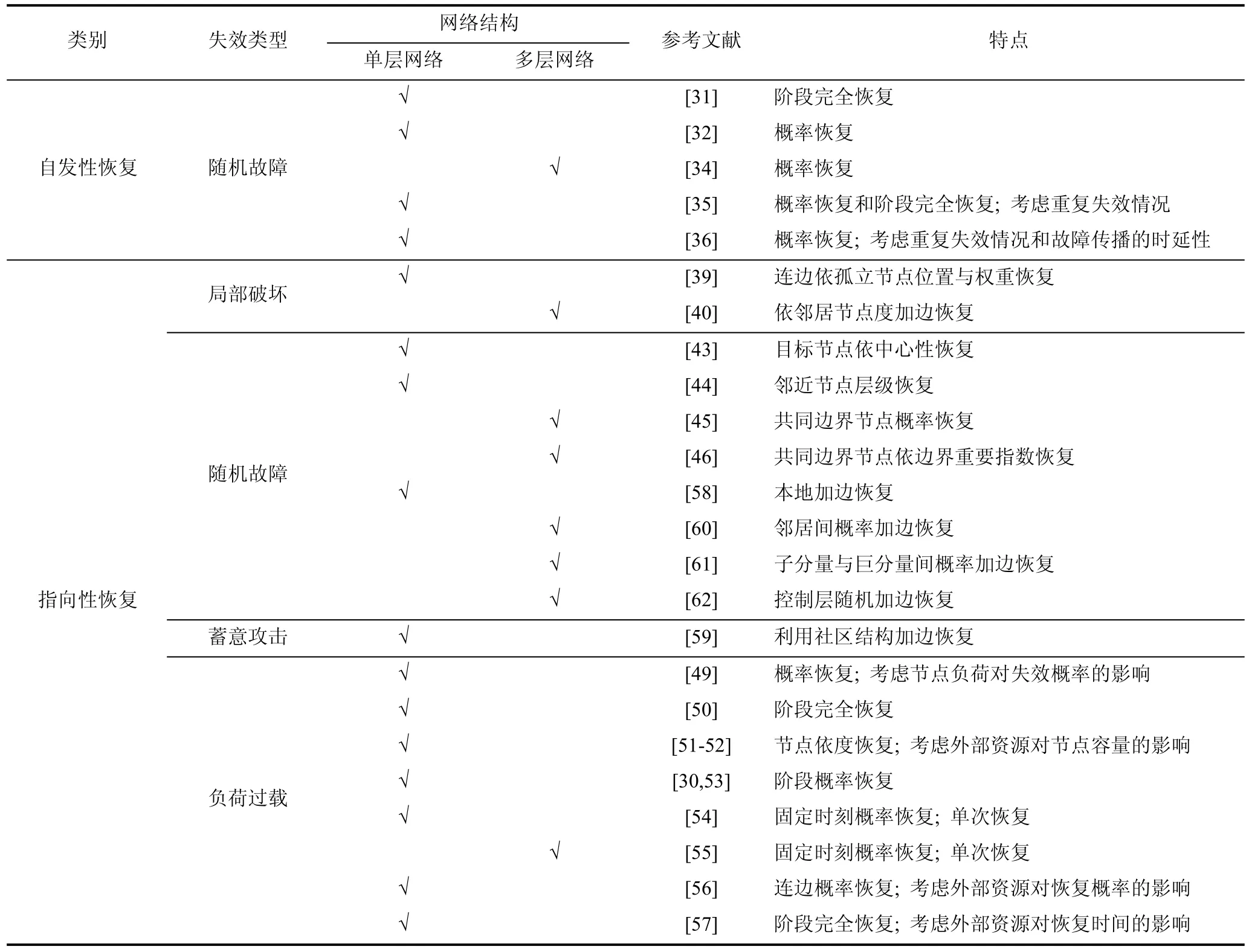
表1 网络恢复机制的文献分类Table 1 Classification of the literature in network recovery mechanism

2.2 评估方法

由于网络类型和功能应用的多样性,当前对网络弹性的具体评价指标尚未达成共识。考虑到一个弹性的网络应能承受一定数量的网元失效、控制级联失效时的网络受损规模、以及在网络受损后能尽快恢复原有功能,近年来一些文献提出了几种概念性的网络弹性评估方法,主要结合网络的失效过程和恢复过程来定义。图1示意了网络失效和恢复过程中性能的变化,其中横坐标为时间,纵坐标为某种网络性能度量。以下对几种网络弹性的评估方法进行简介。

Henry等[27]关注不同阶段网络的状态。如图1所示,t1之前网络为初始状态,(t1,t2)为网络失效过程,(t2,t3)为网络破坏待修状态,(t3,t4)为网络恢复过程,t4之后网络恢复为正常工作状态。他们提出了一种网络瞬时弹性指标,该指标将t时刻的弹性R(t)量化为恢复与损失的比率,表示如下:

图1 网络弹性过程示意图Figure 1 Schematic diagram of the network resilience process

其中,P(t2)是网络处于破坏待修状态时的性能。

Bruneau等[28]提出当级联失效发生后,网络性能随时间改变的大小来衡量网络的弹性R。如图1中阴影所示,阴影的面积越小,网络弹性越强。具体数学表示如下:

其中t1是级联失效发生的时间,t4是网络恢复正常状态的时间。0P是发生级联失效前,网络正常运行时的原始性能,通常为常数,P(t)是时刻t的网络性能。

Ouyang等[29]将整个过程分为三个阶段,如图1所示,t1之前为灾难预防阶段,(t1,t2)为损害传播阶段,(t2,t4)为评估和恢复阶段。这三个阶段可以分别反映灾难攻击下系统的抵抗能力,吸收能力和恢复能力,这些能力共同决定了整个阶段内的系统弹性。进一步,弹性被定义为一定阶段时间(t1,t4)内网络理想正常工作性能与攻击下真实工作性能的比值:

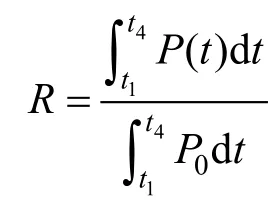
崔琼等[30]依据不同阶段下网络的性能P(t),分别度量网络的状态保持能力a,吸收扰动的能力b和恢复能力c,并定义网络的弹性为R=a∙b∙c,其中:

3 自发性恢复

自发性恢复主要表现为网络中的每个节点或连边在失效之后均有机会自行恢复到正常工作状态,即具有本地决策和独立修复的特性。本节对自发性恢复的相关研究进行梳理,重点介绍基础的自发性恢复模型,包括网络失效和网络恢复等。

自发性恢复的研究中,较为常见的失效与传播可以建模为如下两个过程: (1)内部自生故障: 一个节点在时间间隔t内独立地依概率p发生故障; (2)外部诱发故障: 未发生内部故障的节点为正常节点。如果一个正常节点的邻居节点在时间间隔t中因故障失效的比例大于某一阈值,则该节点也可能依概率p′发生故障。

网络的自发性恢复依据节点能否完全自愈可以建模为两种基础类型: (1)完全恢复: 失效节点在时间段τ≠0之后能从内部自生故障完全恢复为正常状态,在时间段τ′≠0之后能从外部诱发故障完全恢复[31];(2)概率恢复: 失效节点依概率q或概率q′分别从内部和外部故障自发恢复[32]。研究发现,相比概率恢复,完全恢复策略更能增强网络抵御大规模网络故障的能力[33]。

基于上述自发性恢复模型,研究者们主要关注整个网络随时间的动态演化过程[31]。初始阶段内部自生故障占主导,失效传播引发更多的外部诱发故障,导致网络的级联失效。通过控制内部失效概率和外部失效概率得到相图,发现引入完全恢复过程会导致网络具有一阶相变和迟滞(hysteresis)的临界行为,即自发地崩溃和恢复,出现状态切换现象。如图2所示,绿色区域中网络处于高性能状态,橙色区域中网络处于低性能状态,两者重叠的紫色区域则为迟滞区域,即两种状态均可能存在。

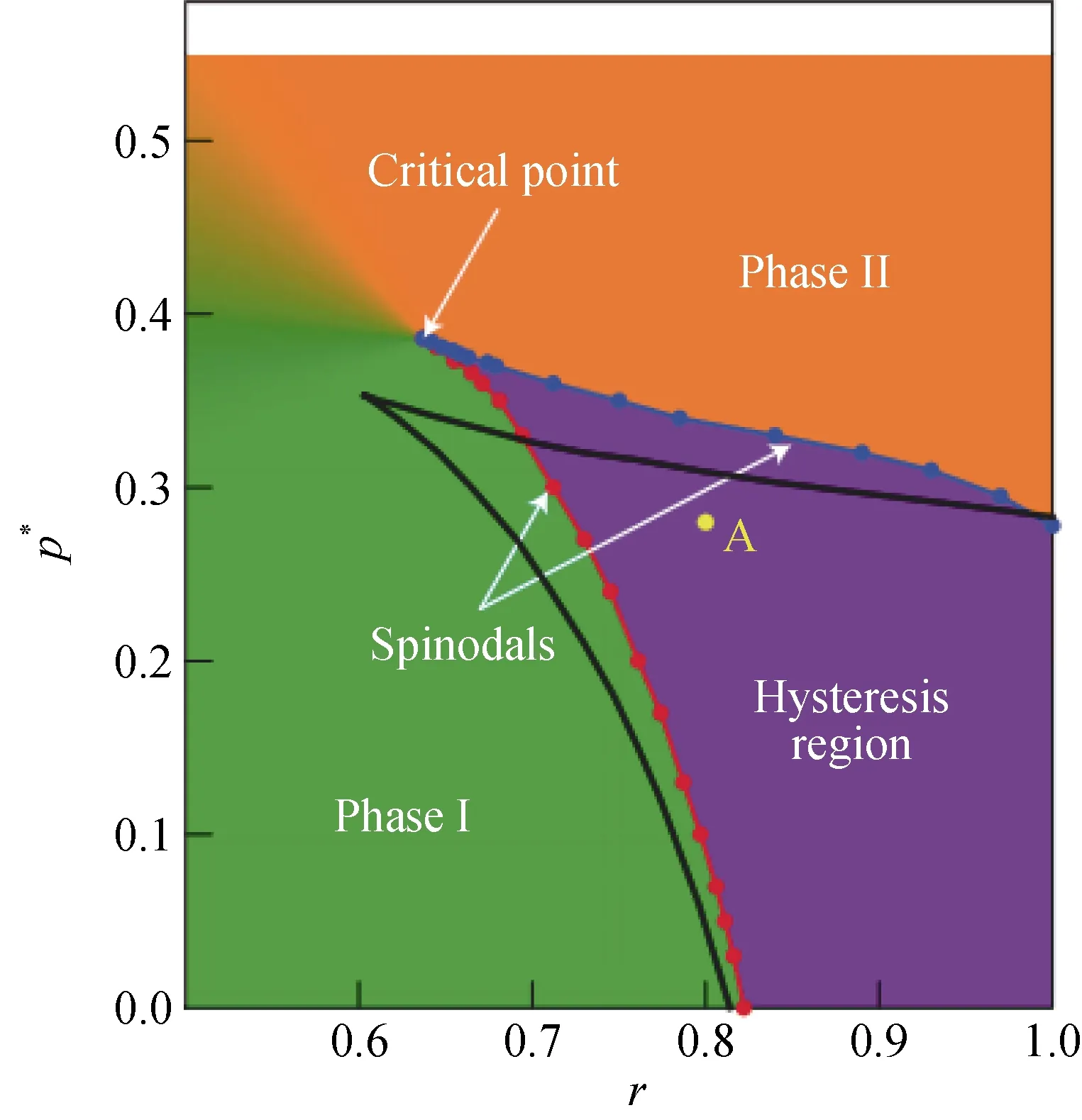
图2 动态恢复过程下的相图(来自文献[31])Figure 2 Phase diagram under dynamic recovery process(from[31])

文献[34]对相依网络上的自发恢复过程进行了研究。特别地,对于一对一连接的相依网络,需要考虑故障通过两个网络间的相依连边传播的可能性,即相依故障: 如果网络中的一个节点发生故障,则有一定的概率p′′,在时间t内使得通过相依连边连接在另一个网络中的节点发生故障。对应地,在完全恢复模型中,节点会在时间段τ′′≠0之后从相依故障中恢复。研究发现相依网络中的相位变换变得更加复杂,如图3相依网络相图所示,四种不同颜色的曲线划分出相互重叠的不同区域,网络在区域中存在的不同状态之间转换。而网络相互依赖的特性使子网络间的状态相互影响,即一个网络状态的转变会引发另一个网络状态的转变。

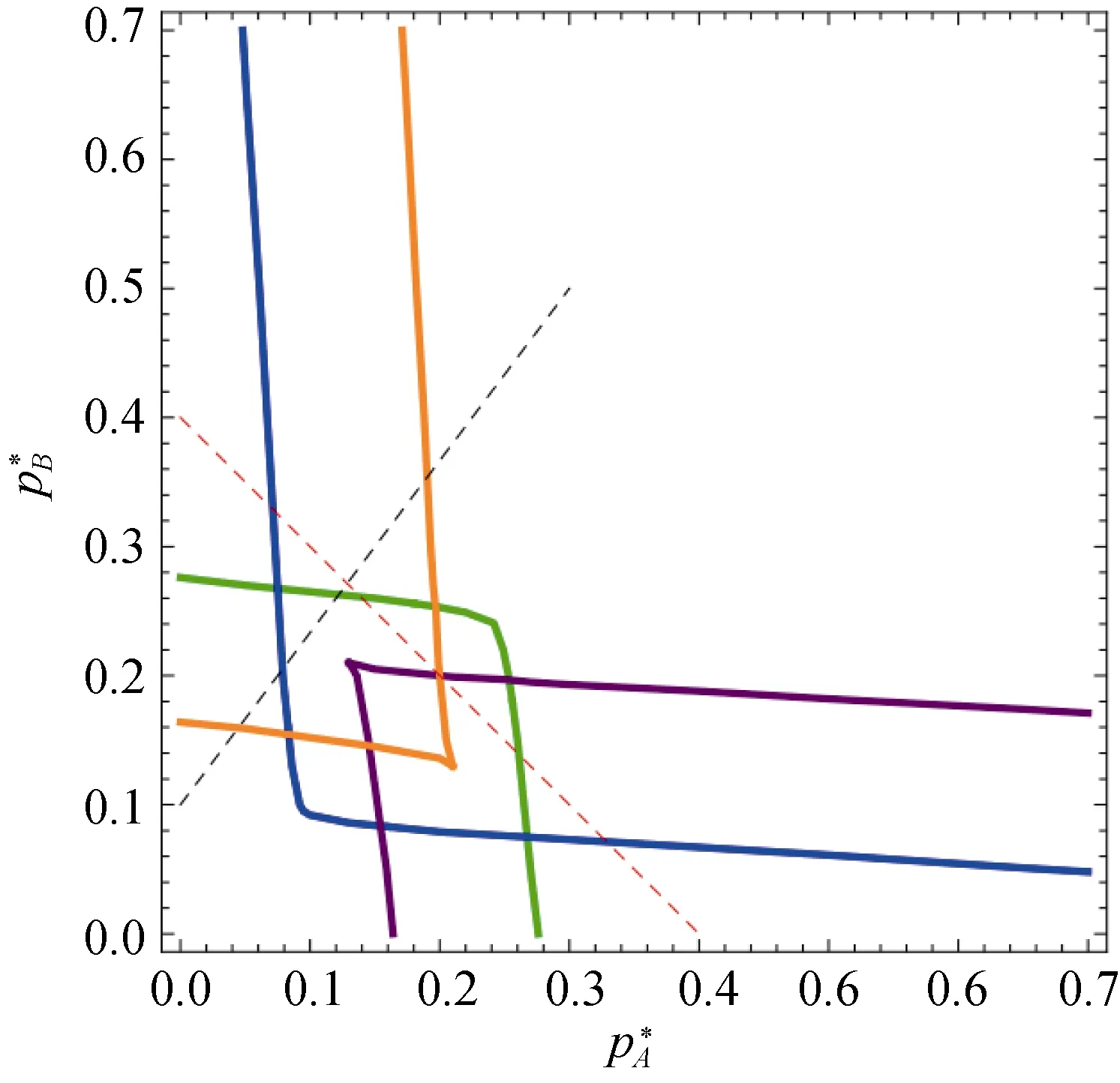
图3 相依网络中的完整相图(来自文献[34])Figure 3 Phase diagram in interdependent network(from[34])

在上述自发恢复模型的基础上,研究者们提出了许多改进模型,更进一步地建模网络的自发恢复过程,并通过调整模型参数设计更好的恢复策略。考虑到现实网络中存在网元的重复失效情况,即网元失效自愈后再次失效,且随着失效自愈次数的增多,网元再次失效的概率也可能逐渐降低。文献[35]定义节点v的失效概率为,其中x为节点v的失效次数,0﹤p﹤1为故障参数。此外,失效传播建模为每个失效节点以概率致使其邻居节点失效。对应地,自发恢复过程建模为概率q恢复和τ时长后完全恢复两种类型。

文献[36]进一步考虑到现实网络中故障传播的时延性,描述网络的动态失效过程为: 节点vi以概率失效,并通过连边传播故障,其邻居节点vj以概率 1 - ( 1 -)kj在一定时τij(α)后失效。其中xi为节点vi的失效次数,0﹤p﹤1为故障参数,kj为节点vj的度。时间延迟值被认为与失效节点和受影响节点都有关系,且度越大的失效节点具有越强的抵御故障传播的能力,能延迟其对邻居节点的影响,定义为:其中0﹤α﹤1为可调参数。特别地,模型假定当节点的失效次数达到某个阈值时,永久失效,从网络中移除。对于自发恢复过程,失效节点vi以概率qki恢复。

对于改进后的自发恢复模型,文献[35-36]研究分析了参数变化下网络级联失效机制和鲁棒性的特征。仿真结果表明,节点的恢复能力随着恢复概率q的增大而增强,失效传播的延迟时间随参数α的增大而增加。增大q和α降低了级联失效的影响,有效减小失效网络的规模,提高网络的鲁棒性; 而随着恢复时间τ和失效概率逐渐增大,网络级联失效过程的速度和规模都呈现出突变增加的趋势,网络的鲁棒性也相应变小。这些结论对于理解网络的自发恢复机制,预防和控制级联失效提供了重要的参考价值。

4 指向性恢复

指向性恢复(directional recovery)从如何高效恢复网络整体的结构和功能出发,对失效网元依据某种策略进行重要性排序后,按顺序进行恢复。对比自发性恢复中,每个失效网元独立地进行本地恢复,指向性恢复立足于网络整体,调配资源进行优先恢复,恢复效率更高。研究者们从不同的角度提出了多种指向性恢复策略,大体可以分为两类: 一种是基于原始网络结构的恢复,通过恢复失效的节点和连边,以达到恢复原始网络结构和功能的目的; 另一种则是改变原始网络结构的恢复,通过向已损坏的网络中添加新节点或新连边以恢复网络功能。

4.1 基于原始结构的恢复

网络恢复作为一种应急机制,主要是在原始网络受到破坏或遭受攻击后展开。以下分别从网络的局部破坏、全局攻击和负荷过载这三类情况对恢复策略进行总结。

4.1.1 局部破坏下的恢复

局部攻击或突发灾害会使得特定区域子网络的节点和连边产生聚集性失效[37-38]。如图4中A和B所示。网络以红色连边为中心受到局部破坏,蓝色和黄色的连边随着与红色连边距离的增大,受到的破坏程度逐渐减弱。两条连边之间的距离定义为从一条连边的中点到另一条连边的垂直距离。灰色区域的暗度越大代表受到破坏的程度越大,当破坏超过承受阈值时连边失效,最后网络中的局部区域剩余黄色孤立节点,越大的节点具有越大的固有权重。Hu等[39]针对局部破坏后的网络提出了两种恢复策略,分别具体介绍如下。

外围恢复策略(Periphery Recovery,PR)[39],将网络巨连通分量中具有至少一条失效连边的节点看作外围节点,该策略优先选择与外围节点之间存在失效连边且权重最大的孤立节点,依次恢复与其相邻接的失效连边。如图4中C1~C3,蓝色连边为外围节点的失效连边。n1为首次选择的权重最大的孤立节点,恢复其上失效连边m1和m2,之后继续选择节点n2,恢复m3和m4。第τ次选择节点,需要恢复的连边 集 合 Lτ为:其中eij表示节点vi和vj之间的连边,ωj是节点vj的权重,P是外围节点集合,Ω是孤立节点集合,A为邻接矩阵。

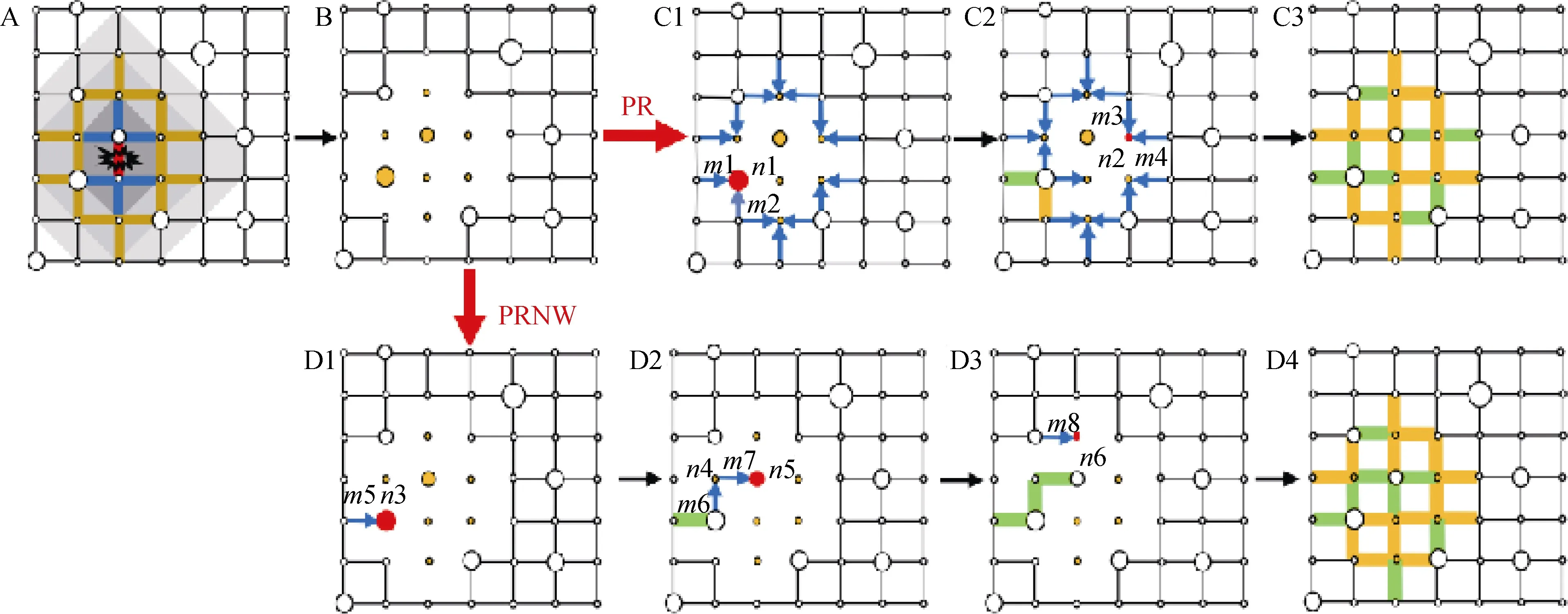
图4 局部攻击及两种恢复过程示意图(来自文献[39]): 图A为局部攻击下的受损网元示意图; 图B为攻击后的网络剩余网元示意图; 图C1~C3为PR下的恢复过程示意图; 图D1~D4为PRNW下的恢复过程示意图Figure 4 Illustration of localised attack and two recovery processes(from[39])

基于节点权重的优先恢复策略(Preferential Recovery based on Nodal Weight,PRNW)[39],该策略直接选择权重最大的孤立节点,依次恢复其到网络巨连通分量中最短路径上的连边。如图4中D1~D4,首先选择权重最大的孤立节点n3,恢复连边m5; 然后剩余节点中权重最大的节点n4,选择其到巨连通分量的最短路径上的一组连边,依次恢复连边m6和m7; 之后选择节点n5,恢复连边m8。第τ次选择节点,需要恢复的连边集合Lτ表示为: Lτ=其中eij表示节点vi和vj之间的连边,Path(s,t)是节点vs和vt之间的最短路径上的一组连边,vt是所有孤立节点中权重最大的节点,并且vs是网络巨连通分量中最接近vt的节点,策略按从vs到vt的连边顺序恢复。

对于上述两种策略,Hu等[39]定义恢复效率为网络恢复后的性能与网络失效时的性能之间比值,通过计算机仿真对比策略的恢复效率。研究结果表明,在网络恢复的初始阶段,PR恢复效率要高于PRNW。这是由于权重最大的节点可能远离巨连通网络,它们之间最短路径上恢复的大部分为权重较小节点的连边,使得 PRNW 的恢复水平早期较低。在恢复的连边数逐渐增多后,PRNW 的恢复效率要高于 PR,因为PR重新连接的节点不一定是网络中权重最大的,对整体网络性能恢复的效率较低。特别地,PRNW具有较低的计算复杂度,在提高网络整体连通性上有很好的表现。现实中自然灾害等导致的局部破坏往往出现在基础设施网络上,而基础设施网络具有较强的相互依赖性。但这两类算法[39]主要针对单个网络,在实际应用中有一定的局限性。

Gong等[40]研究了相依网络上节点的局部攻击导致的网络级联失效。不同于前述[39]针对连边的局部攻击,针对节点的局部攻击建模为: 以一个节点为中心,一定距离内的所有节点全部失效,而网络间相依边的存在使得失效在相依网络中传播扩散。考虑到度越小的节点在下一时刻与巨连通分量断开连接而失效的可能性越大,Gong等[40]提出了优先最小度恢复策略(Healing Strategy by Prioritizing Minimum Degrees,HPMD),计算所有失效节点的正常邻居节点对(vi,vj)之间的恢复优先值 H (i,j) = ki+kj,其中ki表示节点vi当前时刻的度。HPMD按恢复优先值的升序在节点对之间建立连边(不允许自环和重边),通过增强较小度的节点的连通性能,阻止失效传播规模,从而能提高网络鲁棒性。该策略针对相依网络、利用节点的局部信息,较适用于实际网络的恢复场景。

4.1.2 全局攻击下的恢复

全局攻击针对网络中的所有节点,依据节点的重要性指标从大到小对节点进行排序,然后选择节点进行攻击,常用的重要性指标包括各类中心性指标,如: 度中心性,介数中心性,接近中心性,K-核指标等[41-42]。如图5所示,红色的节点和连边为基于度中心性选择攻击的节点及对应的失效连边。攻击这些节点后,网络瓦解为多个子分量,图中用不同颜色代表。网络的恢复过程可以看作网络失效的逆过程,传统恢复策略根据失效节点在原网络的中心性指标按照重要性从大到小对节点进行排序,然后依次进行恢复。该类恢复策略针对网络中的所有失效节点,旨在恢复网络的整体功能; 而在现实中,某些目标节点的及时恢复可能比网络整体的完全恢复更加重要。下面介绍近年来提出的全局攻击下针对不同关键节点的恢复策略。

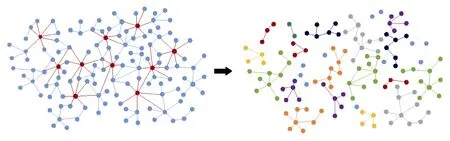
图5 基于度中心性的全局攻击示意图Figure 5 Schematic illustration of global attacks based on degree centrality

Sun和Wang[43]考虑了不同类型的目标节点,如:度较大的失效节点、分布在给定范围内的失效节点等,提出了一种基于目标节点的局部介数中心性的恢复指标,定义为:,其中σst表示节点vs和节点vt之间最短路径的总数,σst( i)表示节点vs和节点vt之间通过节点vi的最短路径的总数,不同于常用的介数中心性,指标中U为目标节点集合。研究结果表明,基于局部介数中心性的恢复策略在使目标节点功能的恢复上表现优于传统恢复策略。类似地,他们[43]定义节点的局部接近中心性为,提出了混合局部介数中心性和局部接近中心性的恢复指标。该混合指标考虑了更多的网络结构特性,在恢复网络效率的效果上比单独的局部中心性表现更好。该类局部中心性指标的提出关注到了具体的恢复目标问题,值得后续进一步研究。

Shang[44]关注距离正常节点较近的失效节点,提出了层级恢复策略: 将完整网络转化为以一节点为中心的层次分布结构。遭受全局攻击后,按照距离中心节点的远近依次恢复失效节点及其连边。该策略的出发点为,现实网络中恢复正常工作节点邻近的节点通常比恢复距离较远的节点更容易。具体地,层次分布结构如图6所示,随机选择一个节点作为中心节点,所有节点按照到中心节点的距离划分为L层,图中每层节点分布在颜色不同的虚线上。假设初始网络中共有1-p比例的节点失效,图中剩余节点为黑色。从中心到外层依次恢复失效节点,同一层的失效节点按随机顺序恢复。当第L层的所有失效节点全部恢复后,才开始恢复第L+1层的失效节点。图中恢复后的节点变为对应层颜色,空心节点为当前剩余失效节点,虚线为当前失效连边,图示状态下将继续恢复第二层中的失效节点。研究结果表明,相比随机恢复策略,层级恢复策略具有更高的恢复效率。值得注意的是,该策略的表现受网络结构特性的影响,度分布较均衡的同配网络中存在“恢复阻力”使得策略效率减弱。因此,需要考虑如何设计不同属性网络下的恢复策略。

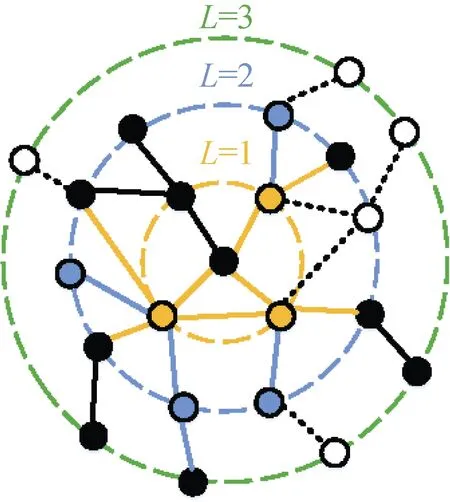
图6 层级恢复过程示意图(修改自文献[44])Figure 6 Schematic illustration of the shell recovery process(modified from[44])

Muro等[45]关注相依网络中与巨连通分量邻近的节点,提出了共同边界节点优先恢复策略。将相依网络中与巨连通分量有直接连边的失效节点集合称之为边界。如果一个子网络边界中的节点与另一个子网络中的边界节点间有一条相依边,则这两个节点称之为共同边界节点。该策略优先恢复共同边界失效节点,并将其重新连接到巨连通分量中。这是考虑到恢复正常工作网络邻近的节点更容易; 此外,不在边界内的失效节点由于未连接到巨连通分量,在相依网络间的级联失效影响下即使恢复也将在下一时刻失效。假设初始有1-p比例的节点随机失效,在级联失效过程中,策略以概率γ恢复失效的共同边界节点。如图7所示,图中空心节点为网络边界。共同边界节点由灰色实线代表的相依边连接,可以恢复; 而灰色虚线代表的相依边的两端不为共同边界节点,故不能恢复。研究发现存在一个与失效比例相关的临界恢复概率,超过这个概率,级联失效就会停止,网络完全恢复到初始状态; 而低于这个概率,网络就会突然崩溃。该策略指出网络完全恢复的可能性,在恢复受损基础设施网络方面具有指导性意义。

图7 边界节点恢复过程示意图(修改自文献[45])Figure 7 Schematic illustration of the boundary nodes recovery process(modified from[45])

考虑到现实网络资源的有限性,吴佳键等[46]对共同边界节点优先恢复策略进行了改进。利用共同边界节点在巨连通分量内外的连接边数定义边界节点的重要性,提出一种基于连接边的择优恢复算法。在恢复过程中,遍历相依网络中某一子网络上的共同边界节点,计算节点的边界重要指数,按降序恢复比例γ的节点,对应子网络的耦合节点同样恢复正常。边界失效节点vi的重要指数Ii定义为:,其中表示边界失效节点vi与同网络的巨连通分量内正常节点存在的失效连边数,表示边界节点vi与同网络的巨分量外节点存在的失效连边数,参数 β ∊ [ 0,1]代表两类连边的比重。该算法在资源有限的情况下,能高效的恢复更重要的边界节点,从而提高网络的结构连通性并控制相依网络间的级联失效。

4.1.3 负荷过载下的恢复

前述的局部破坏和全局攻击下的网络失效模型可以理解为静态网络的失效过程: 一个节点失效,则与其相邻的连边同时失效; 一条连边失效,如果其两端连接的某个节点变成孤立节点,则该节点也失效。除此之外,还有一种负荷容量模型下的动态失效模型[47]: 在静态的网络结构之上,节点和连边还承载一定的负荷,如电力系统的电流,计算机网络的数据流等。网元承载的负荷不能超过其容量限制,当一个节点或连边失效,其邻接网元不一定失效,但该失效网元会将其原始承载的负荷按照某种预设策略分配到其邻接网元或其他正常网元上。若这些正常网元的负荷超过自身的容量限制,再次产生网元失效和负荷重分配。该过程可能反复进行下去,导致更多网元的承载负荷超过容量限制,产生网络的级联失效现象。如图8所示,蓝色节点的大小代表其负荷,在此图中被定义为通过该节点的最短路径的数量,黑色圆圈代表节点的容量。在t=1时,箭头指向的节点发生故障,这将改变其余节点的负荷,在之后的时刻,部分节点负荷超过其容量失效,网络出现级联失效现象。负荷容量模型下的恢复机制可以从恢复概率和恢复时间两个角度进行建模。基于恢复概率,李钊等[49]

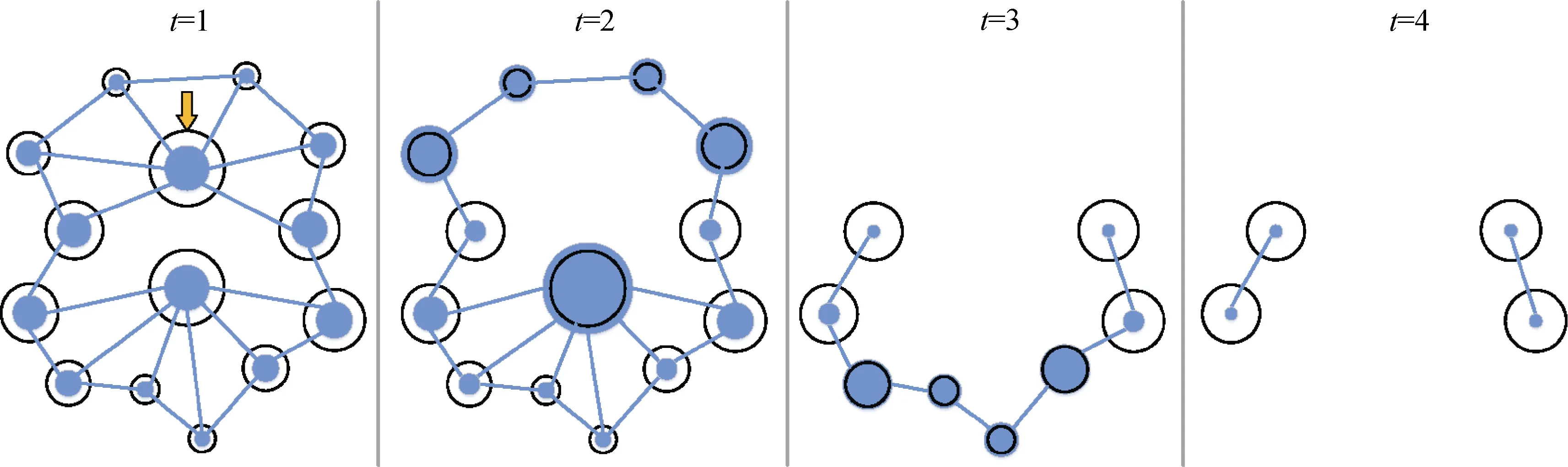
图8 负荷容量模型下网络的时间演化示意图(修改自文献[48])Figure 8 Schematic illustration of the time evolution of the network under load-capacity model(modified from[48])

建模网络的应急恢复机理为节点在过载失效后的每个时刻都有一定概率ρ能够恢复正常。在基础的负荷容量模型下,某一节点移除后,其邻居网元按比例承担一定负荷。考虑到实际网络中部分节点在其负荷超出容量的时候不会立即失效,而可能以过载状态低效率工作。李钊等依据负荷和容量之间的关系提出了不同的失效概率,分别对应不同的节点状态: 当负荷没有超出容量时,节点失效概率为 0,处于正常状态; 当负荷超出容量规定比例时,节点失效概率为 1,处于失效状态; 而当负荷大小处于两者之间时,失效概率随负荷线性增长,节点处于过载状态。研究结果表明,恢复概率ρ对网络效率和网络故障率有很大的影响,越大的恢复概率越能有效减缓网络效率的降低速度和网络节点故障率的增长速度。

基于恢复时间,Fu等[50]将恢复机制建模为依据中心性指标选择的失效节点在τ时刻后恢复正常。为减少失效节点对网络功能恢复的影响,恢复后的节点在恢复自身功能的基础上还应同时承担其他失效节点的部分负荷。具体地,恢复节点vi承担的失效节点的负荷为:,其中Пi为节点vi的失效邻居节点集合,来自失效节点vj的负荷,Li为节点vi的初始负荷,Гj为节点vj的邻居节点集合。当来自失效节点的负荷超出恢复节点的冗余容量时,该节点将再次失效。研究发现,延时恢复策略可以降低对外部资源的需求,且延时时间越大需求越小,但同时网络的恢复效率随之降低,选择合适的恢复延时可以有效缓解网络恢复效率与外部资源之间的矛盾。

和上述模型类似,文献[51-52]提出一种动态的层修复策略(Shell Repair Strategy,SRS): 首先根据失效节点之间的关系构建失效网络; 依据度中心性指标对失效节点按降序排列,依次判断节点恢复后所承担的负荷是否超过其容量; 若没有超过,则正常恢复。否则通过增大容量的方法,使其能够承担已失效节点的负荷。可以看到,该策略能动态对恢复节点进行选择判断,找到那些容量较难承担负荷的节点并进行扩容处理,从而降低了节点恢复后再次失效的可能性,提高了网络恢复的效率。

同时考虑失效节点的恢复时间和恢复概率,文献[30,53]建模了如下恢复机制: 每个失效节点在时间段τ后以概率ρ恢复。研究结果表明,恢复时间的增加使得网路的级联失效规模增大,网络的弹性减弱。当恢复所需时间大到一定程度之后,网络的恢复效率几乎没有增大。相比之下,恢复概率的影响要大于恢复时间,增加恢复概率能显著提升网络的恢复效率。文献[54-55]中采用单次恢复机制: 当到达时间tr时,随机选择网络中在tr时失效的ρ比例节点恢复。研究发现存在最佳的恢复时间点使得网络能维持较好的功能。这些研究更多的关注模型参数变化对网络恢复效率的影响,并在不同类型的网络上进行对比实验,得到的结论有助于今后恢复模型的设计与优化。

进一步地,研究者们考虑在网络恢复过程中,通过投入外部资源来动态调整网元的恢复概率和恢复时间。李树栋等[56]研究了边攻击下的应急恢复机制。具体地,根据负荷与容量的关系,假设连边可能处于三种状态: 正常、拥塞和失效。每条连边都有初始恢复概率,在级联失效过程中,当负荷超过容量时,其会在恢复概率的作用下一定程度地减小; 若负荷仍然超过容量,连边会按其固有权重比例得到一定量的外部资源,使得其恢复概率增大,从而负荷进一步地减小。该模型反映了现实中外部资源越多网络恢复概率越大的现象,并对不同的资源分配方式下的模型表现进行了研究,对启发理解现实网络如何从级联故障中恢复有一定帮助。

Xu等[57]建模了失效网元的恢复时间与资源投入之间的关系。假定在发生级联失效前为节点vi分配的恢复资源为,其中R为资源总量,V为网络节点集合,ki为节点vi的度; β的不同值表示不同的资源分配方法: 为0时,平均分配; 为1时,按节点度的比例分配。失效的节点vi将在一定时间段τi后从故障中恢复,考虑到分配了更多恢复资源的失效节点将比那些分配了较少资源的节点更快恢复,τi定义为服从泊松分布且均值为1ri的随机变量,即:τi~ Poisson( 1 ri)。此外,为了减少已恢复的节点再次失效的风险,恢复的节点将被分配更大的容量。Xu等[57]在资源总量固定的约束下,研究不同资源分配参数对网络恢复性能的影响。结果表明,恢复过程受资源分配方法的影响很大,存在一定范围内的参数使得网络的恢复效率加快,分析发现适当为度更大的节点分配更多资源能有效提高网络的弹性。这些结论为进一步分析复杂网络中的级联失效与动态恢复过程提供了理论基础。

4.2 改变原始结构的恢复

前述恢复策略均致力于恢复原始网络中的失效网元。考虑到现实中存在无法完全恢复或在短时间内很难恢复的失效网元,如: 航空网络中,部分飞行线路受各种因素而取消。研究者们考虑建立新的连边,以连接网络中的剩余子分量,进而恢复网络整体连通性。以下介绍通过增加连边改变了网络原始结构的恢复策略。

文献[58]提出的恢复策略中,节点根据自身的连边损耗来决定是否和一定距离内的节点建立新的连边。具体恢复过程为: 初始网络中比例为p的节点被移除后,每个剩余节点确定其原始邻居中正常节点的比例q: 若比例小于阈值qc,则该节点和距离rmax以内的任意一个正常节点建立新连边,距离以原始完整网络中的路径长度来衡量; 如果最大距离内没有正常节点,则该节点放弃建立新连边。如图9所示,图(a)为原始网络,红色节点为移除的失效节点,红色连边为对应的失效连边; 图(b)为失效后进行恢复的网络,其中黄色节点为正常邻居节点比例小于等于 qc= 0.5的节点,黄色连边为黄色节点和距离rmax=2内的正常节点建立的新连边,可以看到部分黄色节点无法在有效距离内建立新连边。该策略一个明显的优势是利用局部信息,即节点只需要知道其邻居节点的状态信息就可以自主做出恢复决策,因此成本更低; 此外,节点能实时监测自身的连边损耗,在攻击过程中立即进行恢复,相比攻击结束后的恢复更加有效。尽管网络重要节点的失效使得网络分解为多个子分量,但通过增加本地连边能很好的恢复网络的连通性。

图9 局部信息下的恢复过程示意图(修改自文献[58])Figure 9 Schematic illustration of the recovery process under local information(modified from[58])

文献[59]提出了利用网络的社区结构信息来添加连边的恢复策略。其出发点在于,仅利用本地局部信息的恢复的质量较低,而网络全局信息指导下的恢复策略计算复杂度较大。该策略中,将由蓄意攻击产生的孤立子连通分量看作社区,每个社区选择其中一个节点作为代表; 将不同社区的代表节点之间的所有可能建立的连边作为候选连边,依据每个候选连边添加后对整个网络恢复效率的贡献对其进行排序,选择最有效的候选连边进行构建。策略中代表节点的选择也有多种方式,如: 选择度最大节点作为代表节点等。如图10所示,图(a)为原始网络,红色节点为移除的失效节点,红色连边为对应的失效连边; 图(b)为失效后进行恢复的网络。可以将失效后的网络划分为三个社区,橙色节点为每个社区中的代表节点,橙色连边为候选连边; 通过计算可以知道绿色和黄色社区间的候选连边最重要,故选择建立该连边。该策略将局部恢复概念扩展到社区范围内的恢复,能较好地平衡恢复策略的计算效率和恢复质量,并能取得较好的网络恢复效率。之后的研究可以进一步分析社区检测方法对恢复性能的影响等更多问题。

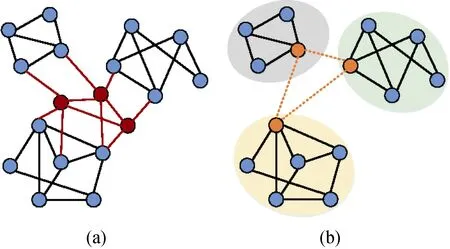
图10 社区结构下的恢复过程示意图(修改自文献[59])Figure 10 Schematic illustration of the recovery process under community structures(modified from[59])

另一类策略则以一定的概率添加特定的连边。文献[60]研究了相依网级联失效过程中的恢复策略:当一个节点被移除或受相依连边影响而失效后,其邻居中任意两个正常工作的节点间会以固定的概率建立新的连边以绕过该失效节点。考虑到相依网络中,与巨连通分量断开连接的子连通分量中的节点会由于缺少连边支持而产生故障,文献[61]提出以一定概率在孤立子分量与网络巨连通分量之间建立新的连边,从而保护子分量,增大巨连通分量,维持网络连通性。需要注意的是,为了维持网络的初始度分布,连边的建立优先选择具有失效连边的节点; 而为了减小子分量再次孤立的概率,在规模大于1的子分量和巨分量之间添加两条连边。如图11所示,图(a)为原始网络,红色节点为移除的失效节点,红色连边为对应的失效连边; 图(b)为失效后进行恢复的网络,黄色的连边为子分量和巨分量间建立的新连边。上述策略作用下的网络产生新的拓扑从而阻止级联失效并延迟网络的崩溃。研究结果表明,随着恢复概率的增加,网络的弹性变大,当恢复概率大于临界值时可能完全抑制网络的级联失效。

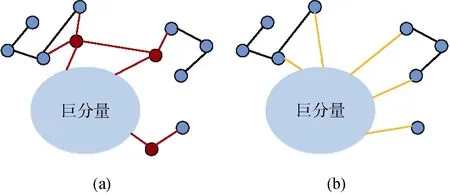
图11 相依网络的恢复过程示意图(修改自文献[61])Figure 11 Schematic illustration of the recovery process under in interdependent networks(modified from[61])

文献[62]研究了访问受限的相依网络上的加边恢复策略。考虑到某些现实多层相依网络中并非所有层级的网络都允许外部访问,该加边策略只能作用在允许访问的网络层中。具体地,初始每层网络中一定比例的节点失效后,失效通过相依边在网络间进行传播。在允许访问的网络层中,每一个失效节点与同层网络中若干个随机选择的节点添加新的连边。失效节点可能主动建立连边,也可能被动与其他失效节点建立连边。若通过新建连边,失效节点能够重新与网络巨连通分量相连,则该节点得到恢复,且其他网络中与之耦合的节点也得到恢复。研究结果表明,通过对允许访问的网络节点进行加边恢复,可以有效的增强整个多层网络的鲁棒性。该策略具有较强的现实意义,如: 在由物理层和信息传输层组成的网络物理网络中,前者由于难以修改其结构而无法控制,但现实中后者的结构可以随时调整,因此可以通过操纵信息层来实现物理层的相关性能。

5 基础设施网络恢复

前述网络恢复的问题建模与策略设计主要基于复杂网络的相关理论,研究过程中做了较多简化假设,如: 无限可用的外部资源、规则的网络模型等。在实际中,许多基础设施网络上的恢复过程往往要考虑更多的现实因素,如: 恢复对象、时间、成本、目标等。研究者们针对不同的约束条件,提出了许多恢复机制,以下进行简单介绍。

通信网络在软件错误或自然灾害的影响下可能出现大规模故障,在有限的维修和人力资源下,无法同时修复所有的故障物理组件,往往要分为多个阶段。考虑到存在部分物理链路在没有完全失效的情况下仍能维持低速率传输,且不同物理组件的重要性和完全修复所需要的资源不同,Wang等[63]定义通信网络恢复问题为: 在每一恢复阶段,可用资源有限,如何从众多待恢复的物理组件中进行最佳的选择,从而最大化恢复网络的总流量。通过对问题进行数学建模,求解得到最优的组件恢复顺序。结果表明,多阶段策略在该类恢复场景下能较好的解决问题,值得进一步研究。

另一方面,通信网络中的服务需求也很重要,仅以网络总流量最大化为目标的恢复策略可能会导致网络中逻辑链路的传输流量不均衡,即在某一恢复阶段某些逻辑链路上的流量比预期的要多,而部分逻辑链路上传输的流量不足或为零。Genda等[64]提出了基于服务需求的多阶段通信网络恢复策略:在选择待恢复物理组件顺序时,平衡网络上总流量的需求和各逻辑链路上的流量需求。特别地,现实中为受影响地区迅速提供服务是网络大规模故障后的关键需求,即使通信质量会在一定程度上下降; 因为人们需要在受灾地区内外尽可能多地进行通信,传递灾难警告,疏散警报,救援请求等信息。考虑到这一现实因素,Genda等[65]将恢复网络的服务作为优先目标,同时考虑合理的流量恢复,提出了目标分解的算法解决恢复问题,确定最佳的恢复顺序。该策略降低了计算复杂度,能更好的应用以解决现实问题。

进一步地,网络中不同服务的重要性不同,且物理组件在不同服务中起到的作用不同。为在有限的资源下尽快恢复网络中的重要服务,Jia等[66]提出了面向不同服务需求的链路重要性指标,并依据其降序确定优先恢复的链路顺序。仿真结果表明,该算法适用于大规模故障下的恢复,但是与网络能达到的最佳的恢复性能之间仍存在一定差距。类似地,Bartolini等[67]提出了基于服务需求的中心性来衡量节点相对于多个服务需求的重要性。为了使得恢复成本最低,提出了一种新颖的迭代拆分和修剪启发式算法,可以在多项式时间内计算节点恢复顺序。实验结果表明,该算法在恢复次数和执行时间上优于其他方法。

现实中,基础设施网络之间往往相互依赖[68],如: 水力系统中的水泵等需要电源才能正常运行,其与电力系统物理上联系紧密; 多个系统共享地理空间,在同一个局部破坏性事件下往往会相互影响。图12所示为不同基础设施网络之间相互依赖关系,和局部破坏下的网络发生级联失效。尽管存在这些相互依赖关系,但基础设施网络之间很少有通信,往往独立地制定其各自的恢复策略。不同网络的恢复优先级的差异,可能导致利益冲突,影响相依网络的整体恢复,如: 一基础设施系统在恢复其他基础设施的需求之前,可能更愿意先为其优先级较高的客户恢复服务。

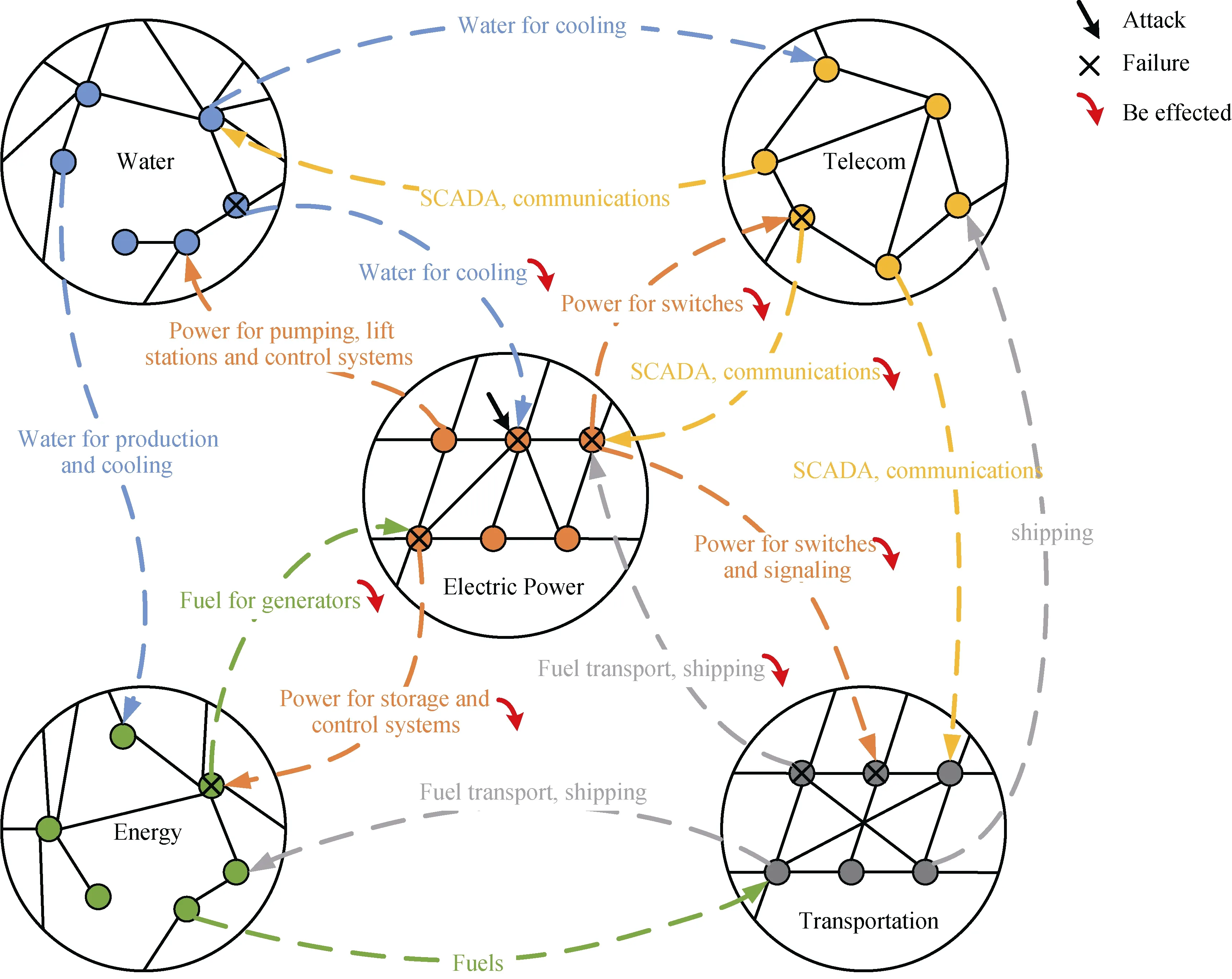
图12 不同基础设施网络之间相互依赖关系和攻击下的级联失效的示意图(修改自文献[69])Figure 12 Illustration of the interdependent relationship among different infrastructure networks and cascading failure under attack(modified from[69])

为解决相依基础设施网络的恢复问题,Sharkey等[70]对比了不同的决策环境,如: 集中式决策环境(仅一个机构计划所有基础设施网络的恢复工作)、分散的决策环境(每个基础设施网络的机构独立进行恢复工作)和信息共享决策环境(基础设施网络之间协作完成恢复工作)。Sharkey等[70]重点研究了信息共享环境下的恢复策略,考虑不同的恢复优先级约束,以最大化基础设施服务需求为目标,设计了混合整数规划模型计算最佳的整体恢复策略。研究结果表明,简单的信息共享能提高整个系统的恢复效率。但是该研究考虑的是理想的信息共享环境,即共享的信息均准确,而实际中的信息可能多次修改,未来不同类型信息共享下的恢复策略值得继续研究。

González等[71]考虑了物理、地理等不同的相互依赖关系,以成本最小化为目标,提出了混合整数规划模型。研究结果表明,该策略不仅能在攻击发生后对网络组件进行恢复,还能在攻击发生前,检测出那些易发生故障的组件,对整个系统弹性的增强有较大帮助。针对基础设施网络间的物理依赖关系,Almoghathawi等[72]考虑不同的攻击场景,如: 随机故障,蓄意攻击或局部破坏,提出了一种多目标的恢复模型,以同时提高网络性能和降低恢复成本。他们指出模型只关注网络组件的两种状态: 正常和故障。而实际中的网络组件可能处于半故障状态,即以低效率工作,故可以在这一方面进行改进。

6 总结与展望

本文介绍了网络弹性的概念,并梳理了两类网络恢复机制的相关研究。网络弹性用于刻画在遭受破坏攻击时网络的防护与恢复能力,构建和运行具有弹性的网络具有重要的现实意义。网络防护作为预防性机制,主要关注如何防止更多的网元失效,从而阻止更大规模的网络崩溃。网络恢复作为应激性机制,主要关注如何修复已失效网元,从而尽快恢复网络功能。本文重点分析了近年来网络恢复机制的相关研究,依据失效网元是各自独立进行恢复还是整体规划进行恢复,将网络恢复策略分成自发性恢复和指向性恢复两类。

自发性恢复的优点是网元只需本地判断状态后自行决策恢复,但缺点是针对性不强,不同重要性的网元有相同的恢复能力,从而网络恢复效率不高;相关研究针对这些问题,考虑到恢复资源的分配问题,关注不同网元的影响力,设计了多参数的恢复模型,得到了许多重要的结论,有利于理解网络的自发恢复机制。指向性恢复则从恢复网络整体的结构和功能出发,计算失效网元的重要性之后依序恢复,具有较好的恢复效率,但是对于大规模网络其在计算复杂度上有较大局限性; 考虑到这一困难,部分研究提出基于目标节点的恢复策略,能较好的解决特定类型网络的恢复问题; 特别地,研究者们提出了一种改变网络拓扑的恢复策略,添加的连边通过分担失效网元的功能能较好的进行应急恢复,但是在现实网络中常难以实现。

总体来看,当前提出的恢复模型多基于较为理想的网络和外部资源环境,而在现实基础网络设施的恢复中还需要考虑网络的服务类别,以及恢复的时间成本等更多实际因素。本文也对基础设施网络上的部分恢复机制进行了简单介绍,容易发现不同功能类型的现实网络的结构特点不同,其恢复需求也不大相同,这对恢复策略的普适性要求会更高;而现实网络的规模和失效影响范围也较模型网络更大,这又对恢复策略的计算复杂度和效率有了更高的需求。

值得注意的是,网络恢复机制的研究总是伴随着网络的失效机制。网络恢复致力于修复失效网元和受损网络,这与网络攻击和级联失效互为逆过程,两者目标正好相反。恢复策略的设计往往会针对网络的失效类型,即: 随机故障、蓄意攻击和局部破坏。网络级联失效在过去20年得到了大量研究[73-78],而近些年网络的恢复机制得到了重视,也初步取得了一些成果,但在以下方面仍需继续深入研究。

(1) 级联失效进行过程中结合防护的恢复策略。已有的恢复策略仅关注网络中的失效网元的恢复,而部分正常网元可能在下一时刻失效,对网络崩溃造成巨大影响。因此,如何在级联失效过程中,既考虑已失效网元的恢复,也考虑未失效网元的防护,提高网络的恢复效率,是网络恢复策略深入研究的重点。

(2) 局部信息下基于深度强化学习的恢复策略。已有的自发性恢复策略效率不高; 全局的指向性恢复计算量大,不易实践; 现有的仅利用本地局部信息的策略恢复质量较低。深度强化学习是一种新兴的决策方法,利用深度神经网络在不断交互中做出目标最优的决策。因此,考虑利用深度强化学习技术,根据每个网元一定范围内的邻居信息,以网络恢复时间最短和恢复程度最高为目标,设计高效的恢复策略,是网络恢复策略在创新方面值得研究的重要问题。

(3) 资源分配下基于网元集合的恢复策略。已有的指向性恢复策略大多基于重要性依次为单个网元分配资源使其恢复,而在资源约束下能恢复的节点集合对网络弹性的影响有时更大,即存在资源需求小的多个网元比资源需求大的单个网元更重要的情况。因此,如何评估单个网元和网元集合的重要性,合理分配恢复资源,是网络恢复策略研究面临的挑战。