不同波形的波纹钢拱桥力学性能分析与测试
蔺 广 花
(延长油田股份有限公司吴起采油厂,陕西 延安 717600)
1 概述
目前,我国道路桥梁方面的建设多采用圬工砌体及钢筋混凝土组合结构等传统材料,也采用钢波纹板结构等新型材料进行桥梁建设[1,2]。传统材料进行桥梁建设存在很多缺点,如工期长、地基承载力高、沉降不均匀等[3,4]。
钢波纹板拱桥是一种采用波纹状弧形板,通过连接、拼装形成拱桥的新型钢结构形式。钢波纹板相较于传统材料具有自重轻、方便运输、施工简单、变形适应好和抗拉、剪和疲劳性能等优势[5]。曹海洋和唐阳使用有限元法对比了波纹钢管涵与圆形钢管涵的受力性能,发现波纹钢管涵的结构变形小于圆形钢管涵的结构变形[6]。陈玉留等采用有限元分析法,发现波纹钢在正常荷载和泥石流荷载条件下均能够满足明洞支护结构变形与受力的要求[7]。Yeau等基于钢波纹管涵洞在静态和动态的汽车荷载作用下挠度和应变变化的研究,发现涵洞的挠度随着填土高度的增加非线性减小,动态汽车负荷下,涵洞的最大挠度比静态汽车负荷下的最大挠度减少10%~30%,且与汽车的总荷载无关[8]。Manko等对钢波纹板桥涵进行静力测试,测试结果表明有限元计算出的应力和平均位移结果比实测结果高,且与结构的永久变形无关[9]。D.Beben研究了钢波纹板涵洞的位移和应变,发现在涵洞管顶1/4位置处位移最大,在管侧1/4位置处应变最大[10]。M.Ju和H.Oh基于波纹钢板螺栓连接的静力和疲劳性能研究结果,发现波纹钢板涵洞桥与传统桥梁相比是最适合桥梁快速重建的纽带[11]。
随着国内越来越多的地区修建波纹钢拱桥来代替传统桥梁结构,如何选取合适的波纹钢拱桥参数是急需解决的难题。本文采用柔性薄壳波纹钢结构建设新型桥梁,使用有限元法分析不同波形中小跨径波纹钢拱桥的力学性能,并与现场实测数据进行对比,为以后的研究及应用提供参考。
2 材料与方法
2.1 有限元仿真建模
结合工程实际及文献调研,仿真过程中钢波纹板简化为壳体,选用Shell63单元,拱外部分简化为实体单元,选用Solid45单元。波纹钢拱桥结构材料的属性参数如表1所示。

表1 材料属性参数
以不同波形的波纹钢为研究对象,采用有限元软件建立不同的仿真模型,各仿真模型的结构参数如表2所示,并对中小跨径波纹钢拱桥波峰和波谷处的挠度和应力的变化规律进行对比分析。选择各仿真模型周向0°,15°,30°,45°,60°,75°和90°断面处的数据进行对比分析。

表2 不同波形模型结构参数
2.2 现场测试方案
根据现场试验条件,波纹钢管内上凸处为波峰,下凹处为波谷。测点布设位置均按照0°,15°,30°,45°,60°,75°,90°,105°,120°,135°,150°,165°和180°的15°间隔均匀布置。定义0°与180°截面为拱桥的拱脚,90°截面为拱桥的拱顶,如图1所示。

本文现场试验包括应变和挠度测试,且两项测试同时进行。具体工况如图2所示。截面1为道路中心线位置,距离道路中心线2 m处为截面2,在截面1和2波峰及波谷的径向位置粘结应变片。
使用静态应变采集仪对施工现场的中小跨径波纹钢拱桥在车辆荷载作用下的应变值进行测量。采用千分表测量波纹钢拱桥的挠度值,以90°挠度为主。挠度测试与应变测试同时进行。图3a)为粘贴应变片的过程,图3b)为采集数据的过程,施工现场建造的波纹钢拱桥如图3c)所示。


3 结果与分析
3.1 波峰有限元模拟分析
由图4~图6可以看出,四种不同波形波纹钢拱桥挠度的绝对值整体沿着0°~90°的位置逐渐增大,方向均向下。在0°~30°截面处,四个拱桥模型的挠度绝对值基本相同;对于其他角度截面上的挠度绝对值,模型A1>A2>A3>A4,表明随着拱桥的波距和波高增大,挠度绝对值减小。四个模型在0°截面处均表现为拉应力,且从拱脚至拱顶的方向拉应力逐渐减小,然后均表现为压应力,随着波距减小,拉应力绝对值增大,但切向应力绝对值近似相等,模型A4的切向应力绝对值略小于其他三种模型的切向应力绝对值。压应力绝对值的变化规律为先增大后减小,在60°处又逐渐增大直至拱顶处。四种模型的等效应力均表现为拉应力,等效应力值均先增大后减小,之后略有增大。在45°,60°及75°截面处,四个模型的等效应力值基本相同。其余截面处,模型A1>A2>A3>A4的等效应力值。
3.2 有限元模拟分析波谷变化规律
由图7~图9可以看出,四种不同波形波纹钢拱桥的挠度绝对值从0°到90°位置逐渐增大,在90°位置均达到最大,且挠度方向均向下。随着波距的增大,挠度绝对值逐渐减小。四种模型的切向应力均表现为压应力,均先减小后增大。模型A1>模型A2>模型A3>模型A4的切向应力绝对值。四种模型的等效应力均表现为拉应力,且应力值在30°与90°截面处基本相等,在其余截面处,波距越小,等效应力值越大。


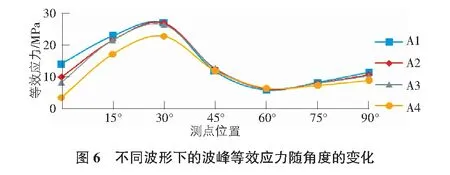

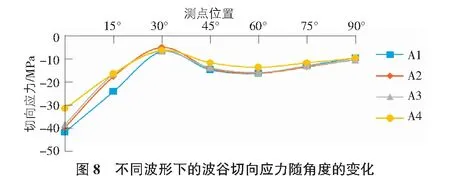

3.3 有限元模拟对比分析波峰和波谷变化规律
由图1~图6可知,模型A1波峰和波谷处挠度变化规律基本相同,挠度方向均向下,且挠度绝对值从0°到90°逐渐增大;波峰、波谷处切向应力的变化规律存在明显差异,模型A1在0°截面处的应力为拉应力,其他三个模型均为压应力;波峰、波谷处等效应力的变化规律完全相反,且均为拉应力。在截面的0°及30°处,波峰与波谷的等效应力的差值和切向应力绝对值的差值均为最大值,可知在这两处存在明显弯矩。
模型A2波峰和波谷的挠度方向均向下,且挠度变化基本一致;拱脚处波峰的切向应力为拉应力,波谷的切向应力为压应力,拱脚处波谷的切向应力绝对值大于波峰的切向应力值,且在拱脚处的弯矩最大。拱顶处波峰和波谷的切向应力绝对值的差值与等效应力值的差值均最小。模型A2波峰切向应力绝对值在拱脚处为拉应力,再逐渐减小到0,然后逐渐增大,在30°又减小。波谷的切向应力绝对值先减小然后增大。
模型A3波峰和波谷处挠度绝对值沿着拱脚到拱顶的方向呈现逐渐增大的趋势,且波谷处的挠度略大于波峰处的挠度,方向均向下。波谷处切向应力及等效应力均先减小然后增大之后略有降低,而波峰处的变化规律与之相反,且纵向看来,波峰和波谷切向应力与等效应力值均存在明显的数值差,在15°与90°处差值较小。波谷切向应力与等效应力最大值均在0°处,最小值均在30°处。
模型A4挠度、切向应力和等效应力的变化规律与其他三个模型的变化规律相同,即挠度从拱脚到拱顶方向增大,且波谷的挠度值略大,方向均向下;波谷处切向应力和等效应力值均先减小,再增大,然后略有降低;波峰的切向应力在拱脚处为拉应力,在其他角度处与波谷的变化规律相反。
3.4 现场实测值与有限元模拟值对比分析
由图10可看出,波纹钢拱桥截面1波峰和波谷处的应力都发生明显的变化。截面1在0°与180°处,波峰均为拉应力,从0°~180°应力变化规律为:拉应力→压应力→拉应力的变化过程。拉应力最大值为18 MPa。在截面1的180°处,波谷的应力绝对值最大,应力为57 MPa;在30°处波谷应力最小,应力值为7 MPa,且截面1波谷均为压应力。

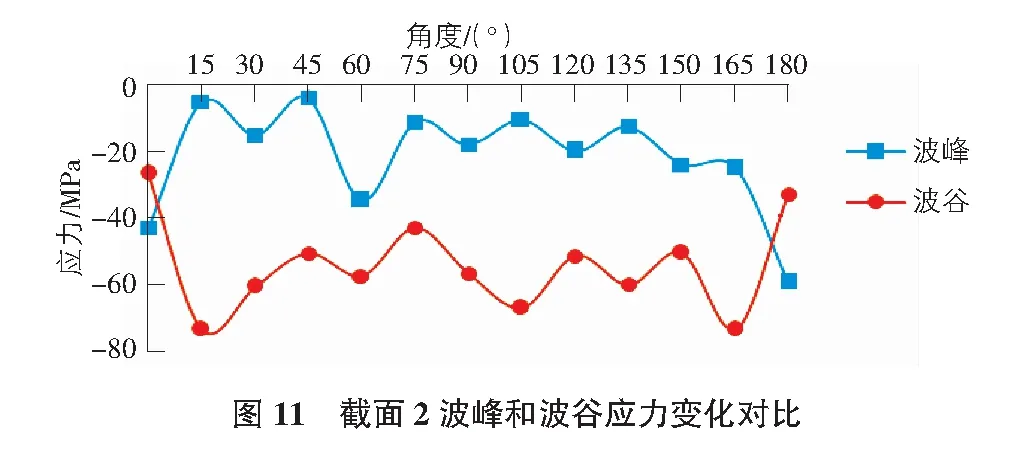
由图11可知,波纹钢拱桥截面2波峰和波谷均表现为压应力,应力值的变化规律基本相反。波峰应力绝对值最大值在180°截面处,应力值为-59 MPa。截面2波谷压应力绝对值最大值在165°截面处,应力值为-73 MPa,压应力绝对值最小处为0°处,为-27 MPa。
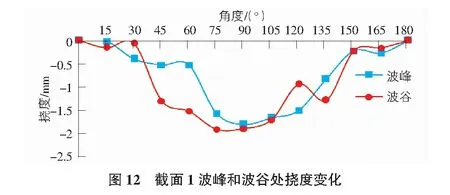
由图12可以看出,汽车荷载作用在拱桥上时,截面1波峰和波谷处挠度变化趋势基本相同。挠度绝对值变化都是从0°到90°整体增大,且最大值均出现在90°处。波峰挠度绝对值最大值为-1.8 mm,波谷挠度绝对值最大值为-1.9 mm。
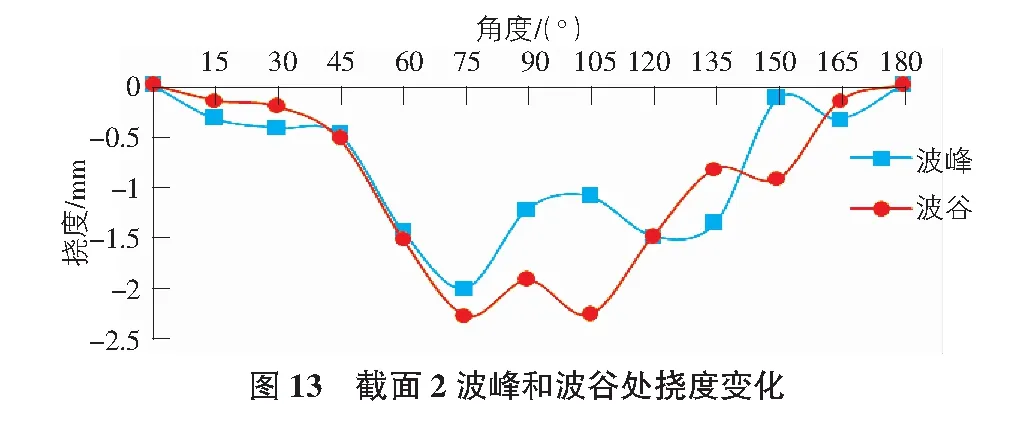
当汽车荷载作用在波纹钢拱桥桥面上时,截面2波峰和波谷挠度绝对值沿0°向90°截面方向逐渐增大。截面2波峰处挠度绝对值最大值为2 mm,波谷处挠度绝对值最大值为2.3 mm(见图13)。
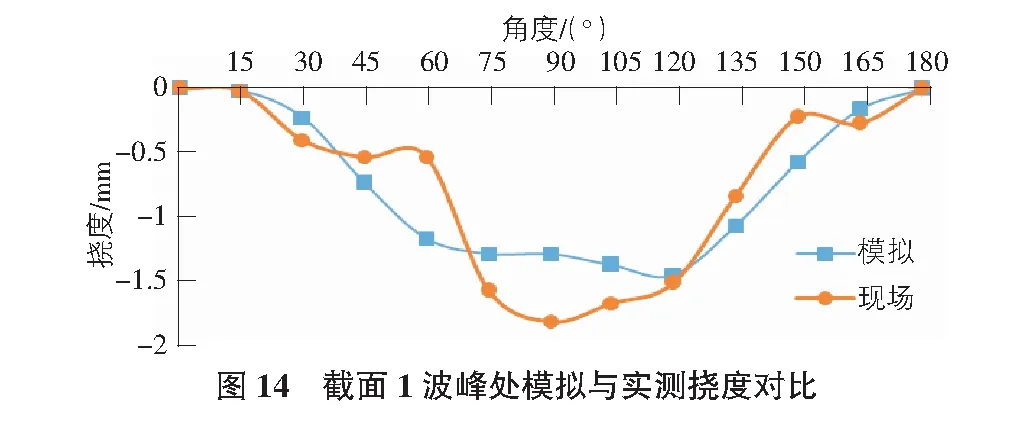
由图14与图15可知,截面1波峰处挠度变化规律的模拟与实测结果基本相同,波谷处挠度模拟值与实测值变化趋势基本相同,现场实测结果明显大于有限元模拟结果,有限元模拟最大值为1.5 mm,现场实测最大值为2 mm。由截面1波峰和波谷挠度对比可以得出,现场值与模拟值之间存在误差,但误差较小。

由图16与图17可知,截面1波峰切向应力在0°处为拉应力,在其他角度位置均为压应力。截面1波谷切向应力均为压应力,在180°处应力值最大。模拟结果与实测结果虽存在明显误差,但误差在可接受范围内,故有限元模拟结果可用于模拟现场工况。
由图18及图19可知,截面2波峰和波谷挠度方向均向下,现场实测结果与模拟结果之间存在误差,且都是从0°到90°逐渐增大。波峰模拟最大值为1.5 mm,现场实测最大值为2 mm;波谷模拟最大值为1.7 mm,现场实测最大值为2.3 mm。综上,波纹钢拱桥在车辆荷载作用下,波峰和波谷模拟结果与实测结果存在误差,误差最大值为1 mm。




由图20与图21可知,截面2波峰和波谷切向应力变化规律完全相反,且均为压应力。波峰切向应力模拟值大于实测值,而波谷处切向应力模拟值小于实测值。波峰和波谷的切向应力实测值与模拟值有一定的误差,但变化规律相同,且有明显的应力应变集中的现象。


由图14~图21可以看出,通过对比分析汽车荷载作用于中小跨径波纹钢拱桥截面1和截面2波峰与波谷处13个测点的挠度与切向应力的模拟值与实测值可以得出,挠度值的实测值与有限元模拟值基本相同,切向应力的模拟值与现场实测值之间存在误差,但变化规律相同,且误差值较小且在合理范围内。因此所建有限元模型与实际工程情况基本符合,同时也证明了针对中小跨径波纹钢拱桥的力学性能问题,使用有限元数值模拟分析法是可行的。
现场实测结果与有限元模拟结果之间存在误差,这是理想化的有限元模型与现场复杂条件下所获得的测试结果之间的差异所导致,主要有以下几个因素:
1)现场实验结果受到测试时间长短、仪器自身及温湿度对应变片的影响而产生误差;2)有限元自身的局限性:有限元模拟过程将实际工况进行简化,无法完全模拟施工现场的实际情况;3)材料力学性能:钢波纹板材质是非均匀的,且板件的拼接、加固等都会对拱桥产生影响,而采用理想化的有限元模型,就会造成波纹钢实测和模型仿真结果存在一定的差异。
4 结语
通过研究波形对中小跨径波纹钢拱桥的力学性能的影响可以得出,随着波距的增大,拱桥的挠度绝对值、切向应力绝对值及等效应力值均减小,且在拱脚及30°截面处波峰和波谷之间均存在明显的弯矩。
在多种影响因素共同作用下,现场实测结果与钢波纹板拱桥有限元模型模拟结果之间存在误差,但误差较小,因此采用有限元法模拟分析中小跨径波纹钢拱桥的受力情况是可行的。

