基于灰色理论的钢丝绳疲劳寿命预测模型

林 海 曾世龙

（甘肃省特种设备检验检测研究院，兰州 730050）

1 技术背景

钢丝绳由于其独特的螺旋扭曲结构和机械性能，广泛应用于航空航天、交通与建筑等领域。安全可靠地使用钢丝绳，能够确保工程运行的安全性，直接影响着生产效率和人身安全。因此，钢丝绳疲劳寿命的准确预测已在工程实践中获得了广泛关注。

对于各种部件的疲劳行为预测，许多学者提出了疲劳预测模型或方法。Jesus等[1]提出了一种从基础材料的应变寿命数据估计带缺口结构部件的概率应力-寿命（S-N）曲线的程序。Muniz-Calvente等[2]提出了一种概率预测的结构细节和适用于任何疲劳破坏准则的机械零件的疲劳裂纹萌生寿命的方法，并预测了铆接连接的疲劳萌生寿命。赵鑫[3]在充分利用相关钢丝绳疲劳试验的历史数据的前提下，结合现有的钢丝绳小样本试验数据，通过贝叶斯方法预测了钢丝绳的疲劳寿命。现有的小样本条件下，钢丝绳疲劳寿命的预测方法是仅预测简单载荷下钢丝绳的疲劳寿命，无法综合考虑影响钢丝绳疲劳寿命的复杂因素。作为小样本条件下数据预测的一种重要方法，灰色理论在处理小样本复杂的影响因素和多个不确定因素方面具有很大优势。该方法已应用于机械刚性零件和金属材料的寿命预测。谢里阳、李存海、白鑫等[4-6]从不同应力下的同一试验件处于相同概率分位点的角度出发，提出了一种基于样本集聚的小样本P-S-N方法，通过将不同应力水平下的疲劳寿命转化为同一应力水平，实现了对小样本数据的扩充。傅惠民等[7]基于异方差回归分析理论，对S-N曲线上所有试验件的寿命进行了整体统计和分析，实现了多母体联合推断，建立了小样本S-N曲线和P-S-N曲线的检验方法。Chen等[8]提出了一种分层贝叶斯数据扩充的新方法，以集成分层贝叶斯建模和贝叶斯数据扩充来处理稀疏数据专门针对疲劳S-N曲线的问题。唐鸿远、陈柏明等[9-10]创新性地将灰色系统理论应用于材料疲劳寿命预测。

综上所述，基于灰色理论的钢丝绳疲劳寿命预测方法可以确定危险物体的S-N曲线。钢丝绳的断面数据是小样品的整个钢丝绳测试数据。本文将基于灰色理论建立钢丝绳优化的灰色预测疲劳寿命模型，以预测小样本条件下钢丝绳的可靠性寿命数据。

2 钢丝绳弯曲疲劳试验

钢丝绳弯曲疲劳试验的测试对象为6×31SW+FC型钢丝绳，查资料可获得弯曲疲劳试验台和具体试验加载[11]。当钢丝绳发生以下情况时，需判断钢丝绳是否失效，并记录钢丝绳的往复运动次数作为钢丝绳的疲劳寿命。

（1）钢丝绳接头处有4根以上的断丝。

（2）在钢丝绳的非接合区域，6d（d为单根丝的直径，下同）范围内有4根或以上的断丝，30d范围内有8根或以上的断丝。

（3）钢丝绳断裂或变形。

将钢丝绳的循环次数记录为疲劳寿命，在可靠性为0.999 9的情况下处理试验结果，得出不同张力下的可靠性疲劳寿命，如表1所示。

表1 钢丝绳的疲劳寿命数据

3 基于灰色理论的寿命分析

可靠性寿命数据的预测顺序是确定钢丝绳危险部位可靠性S-N曲线的基础。一方面，通过疲劳试验获得小样品的试验数据，并通过数据处理获得不同张力下钢丝绳的可靠性寿命。另一方面，建立改进的灰色预测模型，预测可靠性寿命数据，得到可靠的S-N曲线。

3.1 原始GM(1,1)模型

设数据序列X(0)=[x(0)(1),x(0)(2),…,x(0)(n)]，则x(0)(n)的一阶累积生成序列AGO为：

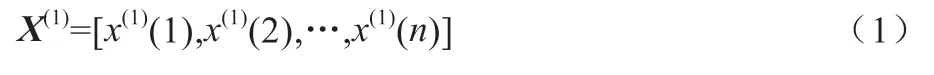
式中，有：

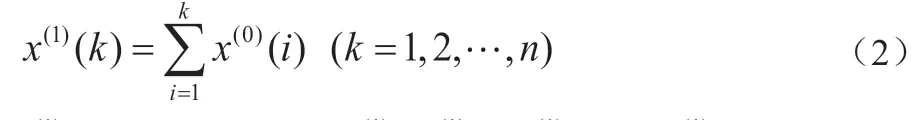
x(1)的紧邻均值序列z(1)=[z(1)(2),z(1)(3),…,z(1)(n)]为：

则原始数据GM(1,1)模型的白化微分方程为：

式中：a为发展系数；μ为灰作用量。

GM(1,1)模型的灰微分方程为：

将k=2,3,…,n代入式（5），可以得到n-1个关于a和μ的方程：

将式（6）展开，可得：

令：

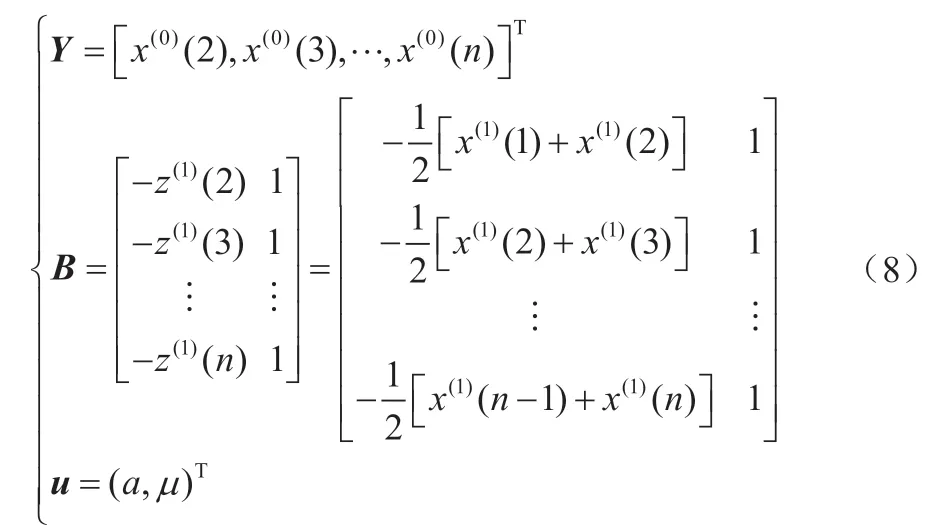
则式（7）可以改写为：

通过最小二乘法，可以得到a和μ：

将求解得到的a和μ代入式（4），则可以得到白化方程的响应解为：

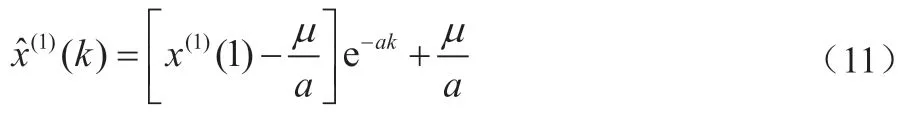
由初始条件x(1)(1)=x(0)(1)，得：

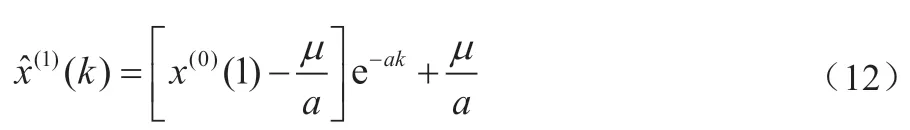
从而可得原始数据序列的预测值：

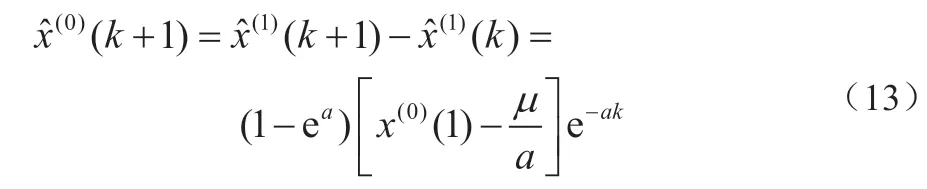
3.2 改进的GM(1,1)模型

在原始GM(1,1)模型中，初始条件为x(1)(1)=x(0)(1)，不能够充分运用原始数据中的信息。将式（13）中的初始条件重新设置为，则白化方程的响应解为：

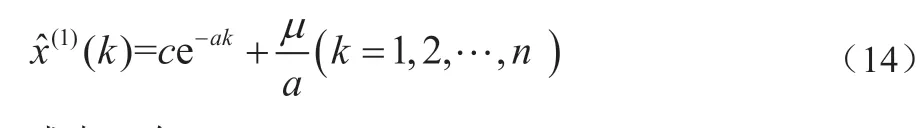
式中，有：

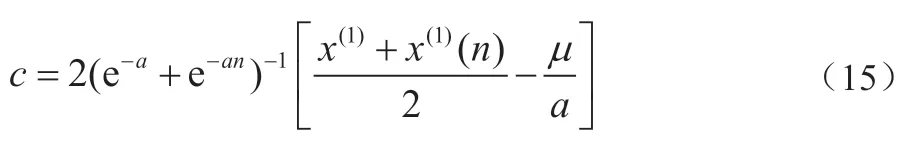
将c值代入式（15），可得：

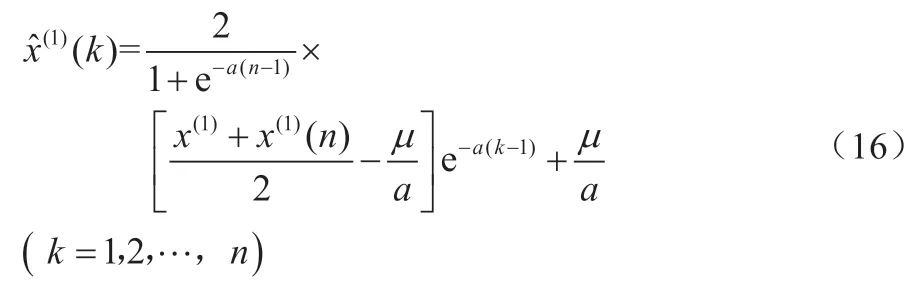
则新的原始数据预测值可以表示为：

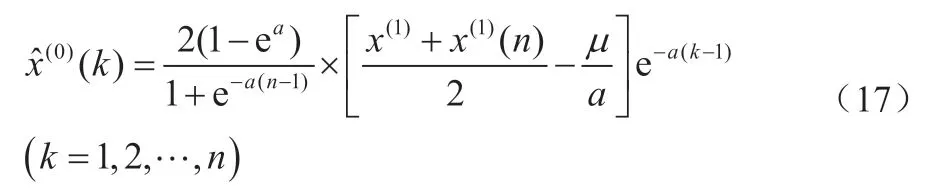
实际工作过程中，随着张力的增加，通常会有许多不确定的干扰因素进入钢丝绳的疲劳寿命预测系统，从而影响寿命的最终预测结果。传统的GM(1,1)模型是基于现有的钢丝绳样品测试数据建立的，无法充分考虑未来因素对钢丝绳疲劳寿命的影响。本文以循环迭代的方式考虑疲劳寿命随拉力变化过程中的干扰因素，反映了钢丝绳的最新失效状态。

灰色预测模型可以灰色处理影响钢丝绳疲劳寿命的复杂几何结构、力学模型和外部环境，降低可靠性寿命数据预测的计算难度。通过引入灰色理论，揭示了数据间隐含的关系，进一步挖掘了数据信息。通过小样本数据处理方法，最后运用所提方法处理钢丝绳疲劳寿命数据，得到了小样本下的钢丝绳S-N曲线。使用改进的GM(1,1)模型预测700～1 200 kN张力下的疲劳寿命，预测结果如图1所示。

图1 预测寿命与试验寿命的对比

由图1可得，理论预测结果很接近试验数据，证明改进的预测模型在考虑了钢丝绳变形或磨损引起的不确定因素的影响和外界环境对寿命预测结果的影响的基础上，不仅优化了求解方法，而且提高了预测精度。

4 结语

经验证，基于灰色理论建立的小样本疲劳寿命预测模型，预测精度较高。此模型通过引入灰色理论，揭示了数据间隐含的关系，进一步挖掘了数据信息，不仅优化了求解方法，而且考虑了钢丝绳变形或磨损引起的不确定因素的影响和外界环境对寿命预测结果的影响。通过利用现有的小样本数据，实现了对钢丝绳疲劳寿命的预测，不仅降低了检测成本，而且大大缩短了材料疲劳寿命的试验周期。