基于FLUENT扭王字块体护面斜坡堤越浪量的数值研究
孙大鹏,修富义,王 键,赵沛泓,董 胜,李玉成
(1.大连理工大学 海岸和近海工程国家重点实验室,大连 116024;2.大连软件园荣泰开发有限公司,大连 116024;3.中交第一航务工程勘察设计院有限公司,天津 300222;4.中国海洋大学,青岛 266100)
越浪量关系着斜坡堤自身结构和堤后陆域的安全性,是斜坡堤设计中重点关注的指标之一。关于斜坡堤越浪量的估算,目前主要采用物理模型试验和数值模拟计算两种方法。由于数值模拟方法不受场地限制,能够克服模型比尺影响等优点,近些年,有很多学者对斜坡堤越浪进行数值研究。Kobayashi[1]和Hu[2]均应用NLSW模型模拟光滑混凝土板护面斜坡堤的越浪过程;Losada[3]和Guanche[4]采用COBRAS-UC模型对斜坡堤越浪量和胸墙受力进行数值计算;王键[5]、杨锦凌[6]均应用FLUENT软件,数值研究光滑混凝土板护面斜坡堤越浪过程,并对坡肩宽度这一影响因素进行了探讨。张九山[7]通过添加多孔介质区模拟护面块体,数值研究护面块体在斜坡堤不同位置时对越浪的影响;王鹏[8]应用FLUENT软件,通过添加多孔介质区,数值研究块体护面斜坡堤爬高过程,建立了惯性阻力系数与糙渗系数的关系;王鑫珏和张庆河[9]以曼宁系数作为等效摩阻系数,研究了人工块体护面斜坡堤越浪的变化;李东洋[10]基于OpenFOAM,通过网格划分工具对斜坡堤外层扭王护面块体进行全尺度精细划分模拟,研究了正相入射不规则波与扭王字块体护面斜坡堤的相互作用;黄宁[11]利用FLUENT软件,基于质量源造波和动量源消波的方法,研究了平台宽度、斜坡坡度对越浪量的影响。前人的数模研究多数是对光滑混凝土板护面斜坡堤越浪量的研究,对块体护面斜坡堤研究较少;在应用FLUENT软件数值模拟块体护面斜坡堤越浪量的过程中,如何简便准确地确定多孔介质区的惯性阻力系数取值一直是该数值方法难以突破的瓶颈。
针对现行《港口与航道水文规范》[12]中尚未给出扭王字块体护面斜坡堤越浪量计算方法的现状,本文应用FLUENT软件,建立多孔介质区数值模型,综合考虑波陡、相对水深、相对堤顶超高、相对坡肩宽度、相对胸墙高度和相对块体尺寸等多种影响因素,数值模拟坡度m=1.5的扭王字块体护面斜坡堤越浪过程,并结合物理模型试验,给出了扭王字护面块体惯性阻力系数C的计算公式。应用该公式,可以较为准确地确定惯性阻力系数,使得FLUENT软件能够独立开展数值模拟,并可以较为精确地计算扭王字块体护面斜坡堤越浪量,为斜坡堤越浪量进一步的数值研究提供了参考。
1 数值波浪水槽
1.1 水槽概况
本文基于唐蔚[13]和王键[5]的主动吸收式造波理论,构建如图1所示的波浪数值水槽,其中水槽全长25 m,高0.8 m,左端为造波边界,右端为6 m长的消波区。

图1 数值波浪水槽(单位:m)Fig.1 Numerical wave sink
1.2 性能验证
不规则波采用JONSWAP谱(γ=3.3),模拟的试验波况如下:有效波高Hs为0.112 6 m,谱峰周期Tp为1.55 s,水深d为0.45 m。在水槽中x=15.0 m和19.0 m两处采集波面数据并对其分析,模拟谱与靶谱的对比见图2,对比模拟波浪与目标波浪的统计波浪要素见表1。

2-a x=15.0 m2-b x=19.0 m图2 靶谱与模拟谱的对比Fig.2 Comparison between the target spectrum and simulated spectrum

表1 有效波高、谱峰周期模拟值与目标值的对比Tab.1 Comparisons of simulated and the target values of significant wave height and peak period
由表1和图2可以看出,模拟波浪与目标波浪的统计波要素及频谱均吻合良好,表明该数值波浪水槽能够有效地模拟不规则波。
2 多孔介质区中惯性阻力系数C的率定
2.1 数模工况组合
采用上一节介绍的数值波浪水槽,运用FLUENT软件,建立多孔介质区模型,模拟计算扭王字块体护面斜坡堤(m=1.5)越浪量,多孔介质模型的方程和边界条件参照王鹏[8],在考虑波浪不破碎的情况下,数值模拟工况组合参照孙大鹏[14]物理模型试验确定,如表2所示,试验断面如图3所示。不同重量的扭王字块体以尺寸h区分,h如图4所示,试验中采用的满足稳定性要求的扭王字块体尺寸h为4.2 cm、6.0 cm和7.8 cm。

图3 试验断面图Fig.3 Shape of test section

图4 扭王字块体尺寸图Fig.4 Shape of the accropode blocks
2.2 惯性阻力系数与越浪量的关系
采用表2中的15种工况组合(参照孙大鹏[14]),h为4.2 cm、6.0 cm和7.8 cm三种扭王字块体,共计数值模拟45组。针对每种工况和不同的扭王字块体尺寸h,建立对应的多孔介质区模型,确定C值的方法如下:
在FLUENT软件中,运用上述建立的数值模型,设定不同的C值,计算出不同C值下的越浪量。以C为横轴,对应C值下的斜坡堤越浪量为纵轴,采用指数函数拟合,得出C与相应越浪量的关系图,本文惯性阻力系数C取值为0.1、0.5、1、2和5。当h=4.2 cm时,表2中不同工况惯性阻力系数C与越浪量的关系如图5中(1)~(15)所示,采用孙大鹏[14]一文中的物模试验值,按图5中虚线所示,查找不同工况下越浪量对应的惯性阻力系数C,得到C值如表3所示。

表2 试验工况组合Tab.2 Combination of the experimental conditions

表3 惯性阻力系数C和数值计算越浪量值(h=4.2 cm)Tab.3 The inertia resistance coefficient and mean overtopping numerical results(h=4.2 cm)

5-a 工况15-b 工况25-c 工况3

5-d 工况45-e 工况55-f 工况6

5-g 工况75-h 工况85-i 工况9

5-j 工况105-k 工况115-l 工况12

5-m 工况135-n 工况145-o 工况15图5 越浪量Q与惯性阻力系数C的关系曲线(h=4.2 cm)Fig.5 Relational graph of Q versus C (h=4.2 cm)
采用同样方法,分别确定出h=6.0 cm和h=7.8 cm时,每种工况下扭王字护面块体的惯性阻力系数C如表4、5所示。

表4 惯性阻力系数C和数值计算越浪量值(h=6.0 cm)Tab.4 The inertia resistance coefficient and mean overtopping numerical results(h=6.0 cm)

表5 惯性阻力系数C和数值计算越浪量值(h=7.8 cm)Tab.5 The inertia resistance coefficient and mean overtopping numerical results(h=7.8 cm)
参照孙大鹏[14]物模试验值,运用查惯性阻力系数C与越浪量关系图的方法,得到表3~5中不同工况的C值。为确定该方法得到C值的合理性,将不同工况下得到的C值代入相应的扭王字块体护面斜坡堤数值模型中计算越浪量,结果见表3~5,以物模试验值为横轴,数模计算值为纵轴,得到两者对比图如图6所示。

图6 Q物模试验值与数模计算值的对比图Fig.6 Comparison of Q between predicted and measured values
从图6可以看出,物模试验值与对应的数模计算值在直线y=x两侧均匀分布,二者吻合较好。说明只要能够合理地确定C,应用FLUENT软件中的多孔介质模型,就可以较为准确地计算出扭王字块体护面斜坡堤的越浪量。
3 扭王字护面块体惯性阻力系数C的计算关系式

(1)


图7 C与Hs/L的关系 图8 C与d/Hs的关系 Fig.7 Relational graph of C versus Hs/LFig.8 Relational graph of C versus d/Hs



图9 C与的关系 图10 C与b1/Hs的关系 Fig.9 Relational graph of C versus Fig.10 Relational graph of C versus b1/Hs



图11 C与的关系 图12 C与h/Hs的关系 Fig.11 Relational graph of C versus Fig.12 Relational graph of C versus h/Hs

(7)C的计算关系式。根据以上分析,本文综合考虑各影响因素,并采用非线性拟合运算,在坡度m=1.5的特定情况下,得到C的计算关系式
(2)
上式相关系数R>0.90,满足拟合方程的相关性要求。表6为不同扭王字块体尺寸在表2中的工况组合下,运用计算式(2)得出相应扭王字护面块体惯性阻力系数C。为确定计算式(2)得到C值的精确性,将表6中的C值带入相应数值模型中计算出越浪量,并与物模试验值(孙大鹏[12])比较,对比结果如图13所示。

表6 公式(2)C的计算值Tab.6 Formula calculated value of C
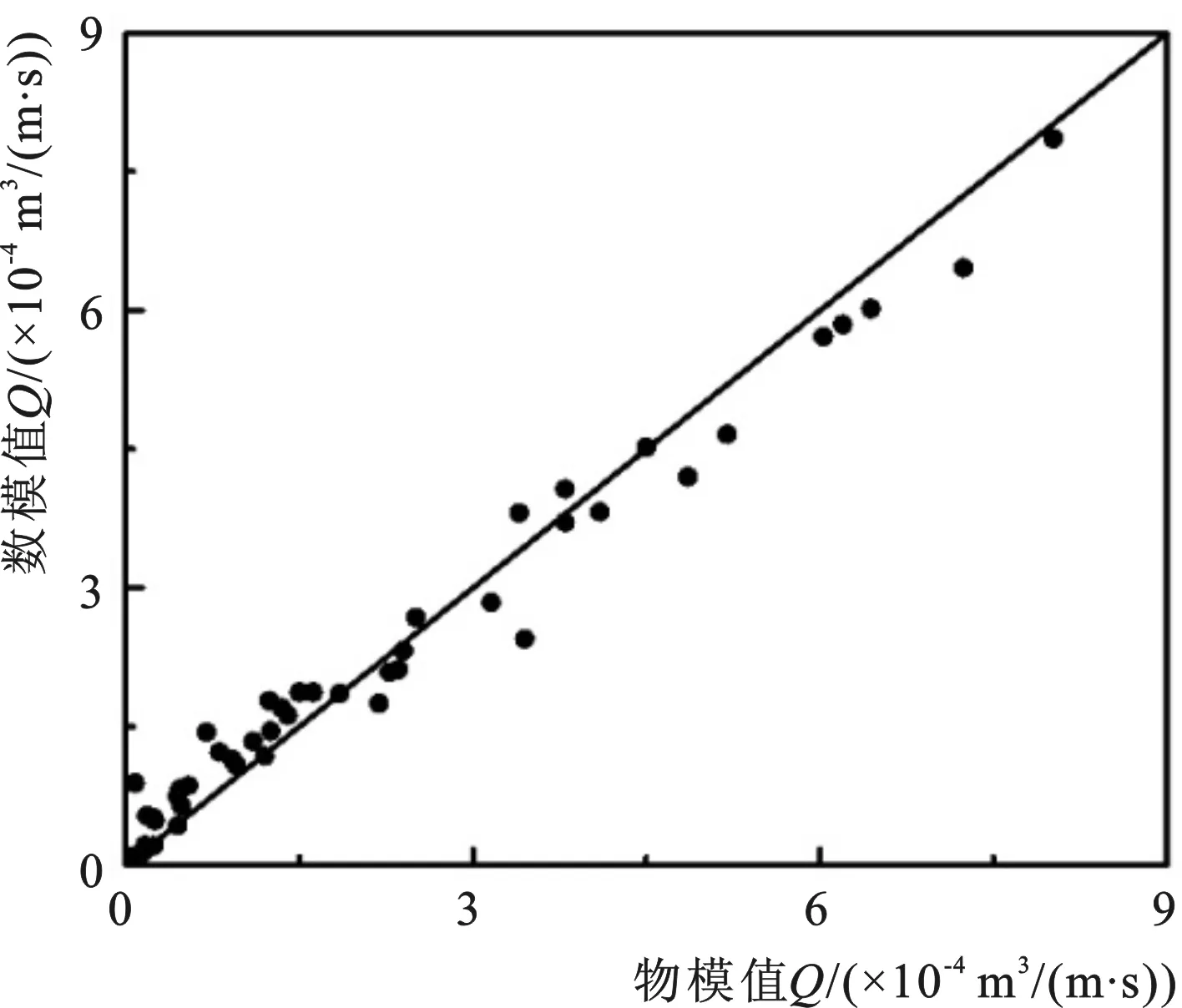
图13 Q物模值与数模值对比Fig.13 Comparison of Q between predicted and measured value
由图13所示,越浪量物模试验值和数模计算值在直线y=x两侧均匀分布,二者吻合较好,表明本文计算式(2)得到的C值具有较好的精确性,在各影响因素处以计算式(2)的适用范围内时,可以直接运用该计算式得到C值,进而数值模拟计算出扭王字块体护面斜坡堤的越浪量。
4 结论
(1)借助FLUENT软件,建立多孔介质区模型,数值模拟得到C与越浪量关系曲线,对应查找物模试验值,确定不同工况下的C值。在此基础上,综合多种影响因素分析,首次得到扭王字护面块体惯性阻力系数C的计算关系式,该计算式考虑因素较多,具有合理性和一定的工程实用性;(2)将计算式(2)得到的C值带回数值模型中计算出相应越浪量,与物模试验值吻合良好,表明本文构建的数值方法具有较好的精确性与合理性。该数值方法为扭王字块体护面斜坡堤越浪量的深入研究开辟了一条新途径,使得FLUENT软件无需借助物模实验,能够独立计算扭王字块体护面斜坡堤越浪量,并对其他种类块体护面斜坡堤的数值研究具有借鉴意义。

