Wrapper特征选择下的序贯三支分类方法
张 璐,刘 盾,杨 新
1(西南交通大学 经济管理学院,成都 610031)
2(西南财经大学 经济信息工程学院,成都 611130)
1 引 言
随着科学技术的不断进步和互联网的飞速发展,人类开始迈入大数据时代.面对数据的爆发式增长,人类需要有效的方法对多源异构数据进行分析处理,各种机器学习算法应运而生.机器学习方法的出现适应了大数据时代的迫切需求,因而被广泛的应用于诸多领域,并取得了巨大的成功.分类作为机器学习的重点研究领域之一,一直受到国内外学者的广泛关注.目前,静态分类器大多是根据给定的属性集合对样本进行分类,在分类过程中没有考虑样本之间的差异性,这会导致信息获取成本大幅增加,整体分类成本过高.例如,在人脸识别任务中,面部特征明显的个体使用清晰度较低的图像就能进行准确判别;面部特征隐晦的个体才需要高清图像进行识别.静态分类器往往只能根据同一粒度的图像对全体样本进行判别.这种无差异的静态判别方法可能会造成信息资源的浪费,增加图像的获取成本.在实际生活中,理性决策者往往可以先利用少量信息对容易分类的样本进行判别;之后再获取更多信息对难以分类的样本进行进一步识别,即:利用不同粒度信息对不同样本进行分类.
三支决策[1-4]是一种以“三分而治”(Trisecting and Acting)为核心思想的决策方法.Yao[5,6]将粒计算的思想引入三支决策,基于粒度由粗到细的多层粒结构,提出了序贯三支决策方法,其核心思想为:随着粒度的增加,利用一系列分治策略对样本进行动态处理.一系列研究表明:序贯三支决策方法可以显著降低决策成本[7-9].一般而言,实现序贯三支决策的关键步骤是构造多层次的粒结构.现有研究主要是通过逐步添加样本属性的方式来构造不同层次粒结构[10-12].然而,已有研究忽略了添加过程中属性的冗余性问题,也没有考虑添加顺序对分类结果的影响.
Wrapper特征选择框架是将特征选择过程与学习器预测结果结合起来的一种学习框架[13],它将学习器作为一个黑箱,利用学习器的精度对一个特征子集的优劣进行评价,并采用一定的搜索策略对特征子集不断优化.大量研究表明,Wrapper特征选择框架能大幅提高学习器精度[14-16].与其他特征选择方法相比,它通常可以获得更好的特征子集[17].目前,Wrapper特征选择框架的优化搜索策略主要分为3类:精确搜索算法,序列搜索算法和随机搜索算法[13,17].精确搜索算法可以保证找到全局最优解,但随着特征数目的数量增加,算法时间复杂度成指数形式上升;序列搜索仅能在很小的解空间进行搜索,通常会导致得到的属性子集距离最优解较远;随机搜索算法根据一定的启发式搜索规则,同时在局部和整体进行搜索,既能保证一定的搜索范围,也能保证较低的时间复杂度.遗传算法作为一种经典的随机搜索算法,对优化问题的数学性质要求较低,能够很好地适用于隐式函数目标.因此,本文采用遗传算法作为Wrapper特征选择框架的搜索策略.
基于上述分析,为了弥补静态分类器的缺陷,本文将序贯三支决策的思想引入分类过程中,利用“三分而治”的动态分类策略和多粒度的静态分类器对样本进行差异化分类;同时考虑到冗余属性和属性添加顺序对分类结果的影响,将Wrapper特征选择框架引入粒化过程中,提出了一种Wrapper特征选择下的序贯三支分类方法,最后通过实验分析来验证所提出方法的有效性.
2 相关理论
2.1 三支决策和序贯三支决策理论
三支决策(Three-way decision)是 Yao[1-4]提出的一种重要的粒计算和不确定性决策方法.作为决策粗糙集的延伸与扩展[18-20],三支决策能很好的处理不确定性问题和代价敏感问题,并在信息、医学、管理和工程领域得到了广泛应用[18].随着研究的不断深入,三支决策逐渐从狭义扩展到广义[20,21],从粗糙集[22,23]扩展到区间集,模糊集[24],阴影集,概念分析,机器学习[25,26]等各方面.Yang[27]和Liu[28]对三支决策的发展进行了全面的总结和回顾,并且指出了未来的新机遇和新挑战.
在三支决策理论中,决策者可以根据决策目标将整体论域分为正域、负域和边界域3个部分.对于3个区域,决策者可以进一步采用接受、拒绝和延迟策略.下面,通过一个评价函数和一对阈值给出三支决策模型中“三分“的定义[18]:
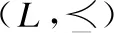
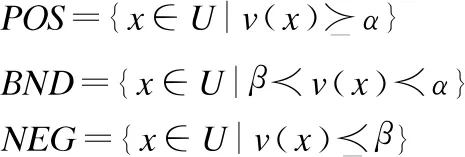
(1)
可以看到,当POS,BND和NEG中当且仅有一个区域为空集时,三支决策退化为二支决策。图1为三支决策的基本模型.

图1 三支决策基本模型
在实际的决策过程中,三支决策的过程往往呈现出动态特征.针对于动态三支决策过程中多层次的粒结构特点,Yao[5-6]提出了序贯三支决策方法.在序贯三支决策模型的每个粒层,每个对象将被划分到正域,负域或边界域中的某一个区域里面.划分到正域和负域的对象能够在该粒层立刻做出接受或拒绝的判断,而划分到边界域的对象将被移动到更细的粒层去做进一步判断,直到最终决策目标实现.
2.2 粒计算
粒计算(Granular computing)是一种模拟人类思维、研究人脑认知和解决复杂信息处理问题的新兴不确定性理论.在序贯三支决策方法中通常需要一个多层次的粒结构实现其动态决策过程.一个粒结构由粒子、粒层和层次结构3个元素组成.粒子是构成粒计算模型的基本单位,是一个问题的抽象模型.粒层是由具有相同粒度的所有粒子所构成的整体,是问题空间在某一粒度下的一种抽象描述.粒度是描述粒子大小的概念.若根据一个有序的粒度关系对层进行排列,则会得到一个层次结构.通常根据粒度的不同序关系,层次结构分为自顶向下,自底向上和自中向外.本文主要采用自顶向下的多层次粒结构.
2.3 基于遗传算法的Wrapper特征选择框架
Wrapper特征选择框架中主要有两个主体部分:一是搜索策略,二是分类器.本文选用遗传算法作为Wrapper框架的搜索策略.分类器需要根据实际需求进行选择,本文选取逻辑回归(LOG)和支持向量机(SVM)两种分类方法进行实验.
在20世纪70年代,John Holland提出了遗传算法(Genetic Algorithm,GA).遗传算法是以达尔文的进化论以及遗传学为基础而提出的元启发式算法,通过优胜劣汰的进化过程来获得问题的最优解.遗传算法对求解问题的性质要求很低,对函数的连续性和可导性没有要求,甚至对没有明确解析式的优化问题也保持良好的全局寻优能力.由于遗传算法良好的适应性,它被广泛应用于人工智能的各个领域[29,30].
基于遗传算法的Wrapper特征选择框架对属性子集变量进行合理编码,产生初始种群,并利用分类器的精度作为属性子集的评价指标,通过精英保留,选择,交叉,变异等遗传算子不断搜索更优属性子集并进行记录,直至收敛或达到迭代次数,最终得到优化后的属性子集.
2.4 等价关系和等价类
假设S=(U,C∪D)是一个信息系统,其中U为论域,C为条件属性,D为决策属性。对于∀a∈C∪D,定义映射fa:U→Va,Va表示属性a的值域。下面给出等价关系与等价粒子的定义[11].
定义 2.给定一个信息系统S=(U,C∪D),A⊆C∪D,则论域U上的等价关系可定义为:
RA={(x,y)∈U×U|∀a∈A,fa(x)=fa(y)}
通过等价关系RA可以定义论域U的一个划分U/RA={[x]|x∈U},[x]为等价类,也称等价粒子。等价粒子中的对象存在不可分辨关系。
如果两个等价关系R1,R2之间存在关系R1⊆R2,则通过R1诱导出的等价类[x]1和R2诱导出的等价类[x]2满足:[x]1⊆[x]2。通常地,可以通过一组有序的条件属性集合定义一组有序的等价关系,实现对论域的多层次划分,进而构造一个多层次粒结构。
3 基于Wrapper特征选择的粒化方法
实现序贯三支分类方法的首要工作就是要建立一个多层次的粒结构.本文将Wrapper特征选择框架引入粒化过程中,提出了基于Wrapper特征选择的粒化方法(Wrapper based Granulation method,WG).
该算法主要分为3个步骤:属性选择,属性排序,基于等价关系构造多层次粒结构.原始条件属性集首先对冗余属性和不相关属性进行约简,之后对属性的添加顺序进行排列,进而构造出一组存在有序关系的条件属性集,最后根据等价关系构造出一个多层次的粒结构,其过程如图2所示.
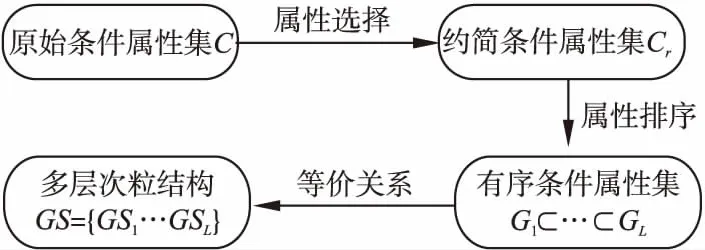
图2 基于Wrapper特征选择的粒化方法
3.1 属性选择
为了消除冗余属性对后续粒化过程的影响,首先利用基于遗传算法的Wrapper特征选择框架进行属性选择,其流程如算法1所示.
算法 1.属性选择算法
输入:信息系统Strain=(U,C∪D),遗传算法参数集GAP(交叉率cp,变异率mp,种群数m,迭代次数n,停止次数q),分类器ψ.
输出:条件属性子集Cr
1.BI=∅BF=0BA=0i=1
//编码1代表选取该属性,0表示不选取
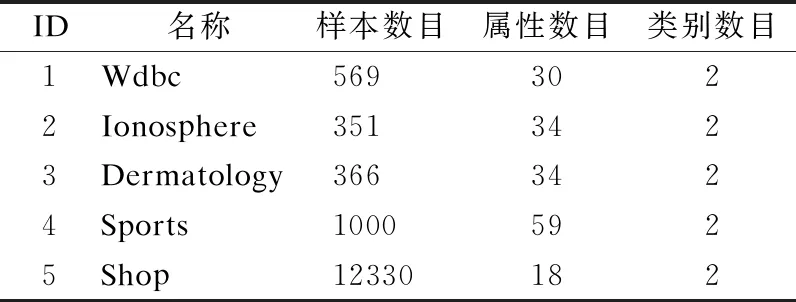
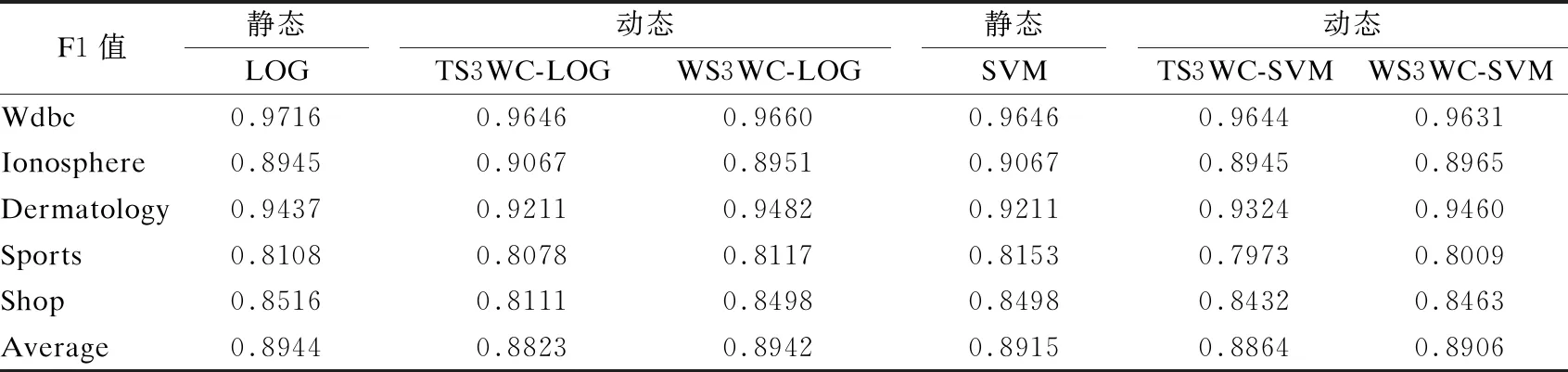
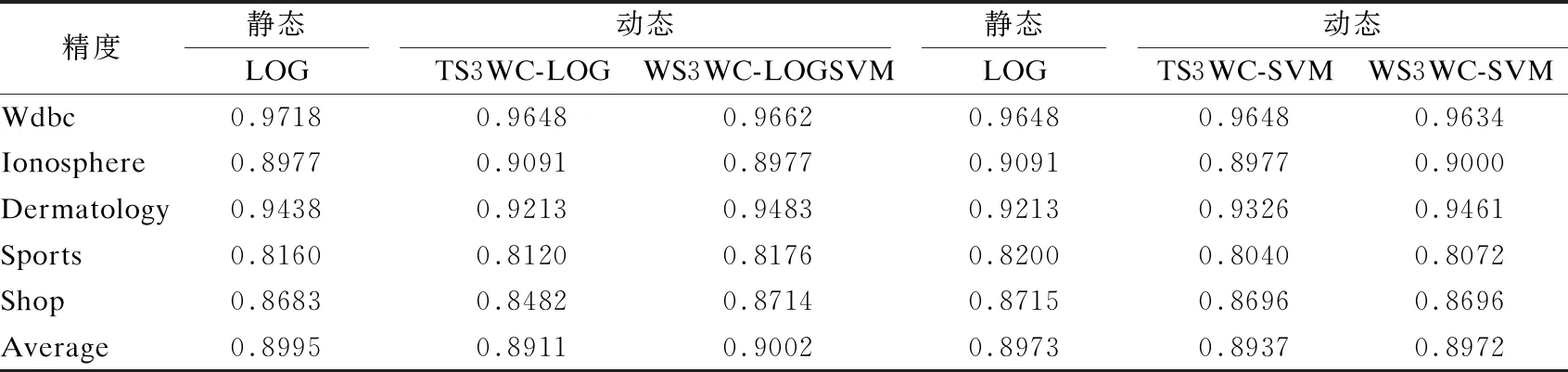
3.while1≤i≤nor|i-BA| 3.1.for1≤j≤mdo 3.1.1.Ej=Crossvalidation(ψ(Sj=(U,Ij∪D)) //对属性子集进行交叉验证 3.1.2.j=j+1 3.2.endfor 3.3.ifmax(Ej)>BF 3.3.1.BI=Imax(Ej)//更新历史最优个体 3.3.2.BF=max(Ej) //更新历史最优适应度 3.3.3.BA=i//更新历史最优轮次 3.4.ifmax(Ej) 3.4.1.Imin(Ej)=BI//精英保留 3.9.i=i+1 4.endwhile 5.returnBI 在属性约简后,如何决定属性的添加顺序也是十分重要的问题.对于每一粒层,都会添加一部分属性以确保下一粒层粒子的粒度更细.如果一些分类能力比较差的属性被优先添加,则会导致分类器在粗粒度的精度很低,误分类成本和延迟成本增加.每一粒层添加的属性均由基于遗传算法的Wrapper特征选择框架选出,其流程与算法1相似,算法2只列出不同的部分. 算法2.单粒层待添加属性的选择算法 输出:本粒层添加的属性集TC … //编码1代表选取该属性,0表示不选取 … 3.1.1.Ej=Crossvalidation(ψ(Sj=(U,(Ij+EC)∪D))) … 算法3.属性排序算法 1.EC=∅LC=Cri=1 2.while1≤i≤L-1 2.2.Gi=EC=TC∪EC 2.3.LC=Cr-EC 2.4.i=i+1 3.endwhile 4.ifi=L 4.1.Gi=Cr 5.endif 通过3.2节,可以得到一组有序的条件属性集G1⊂G2⊂…⊂Gi⊂…⊂GL,据此可以定义一组有序的等价关系EL⊂…⊂Ei⊂…⊂E2⊂E1,进一步地,可以得到其等价粒子存在如下关系: [x]EL⊆…⊆[x]Ei⊆…⊆[x]E2⊆[x]E1 (2) 基于上述分析,可以定义如下多层次粒结构: GS=(GS1,GS2,…,GSL)GSi=(Ui,Ei,Gi,[x]Gi) (3) 为了实现样本的差异化分类,减少分类成本,本文将序贯三支决策的思想引入分类过程中,提出了一种序贯三支分类方法,其基本框架如图3所示. 图3 序贯三支分类方法的基本框架 为了进一步说明序贯三支分类方法的具体过程,第4.1节对动态分类过程中涉及的分类策略进行介绍.第4.2节,结合第3节粒化方法得到的多层次粒结构,提出一种Wrapper特征选择下的序贯三支分类方法. 根据图3的模型框架,对于粒层i(0 接着,对粒层i的三支分类策略进行定义. (4) 其中,正域表示预测属于正类的对象集合,负域表示预测属于负类的对象集合,边界域表示暂时不能划分的对象集合.对于正域POSi(X)对象采取行动aP,即标记为正类,对于负域NEGi(X)对象采取行动aN,即标记为负类,对于边界域BNDi(X)对象采取行动aB,即暂不分类. 然后,分析阈值αi和βi的计算过程.根据表1中的代价矩阵,基于贝叶斯风险最小化原则,可以对三支分类策略的阈值进行计算. 表1 三支分类代价矩阵 在粒层i(0 (5) 根据贝叶斯准则,最佳的行动方案应该是期望损失最小的行动集,于是阈值的计算应该满足如下三条决策准则: (P)若Ri(aP|x)≤Ri(aB|x)Ri(aP|x)≤Ri(aN|x)同时成立,则x∈POSi(X); (B)若Ri(aB|x)≤Ri(aP|x)Ri(aB|x)≤Ri(aN|x)同时成立,则x∈BNDi(X); (N)若Ri(aN|x)≤Ri(aP|x)Ri(aN|x)≤Ri(aB|x)同时成立,则x∈NEGi(X). 最后,结合决策规则(P)-(N),可得到αi和βi的计算公式: (6) (7) 特别地,如果在前L-1粒层不能完全划分样本,则在粒层L使用二支分类策略,二支分类策略定义如下: (8) 其中,正域POSL表示预测属于正类的对象集合,负域NEGL表示预测属于负类的对象集合.对于正域POSL对象,我们采取aP,即标记为正类,对于负NEGL对象,我们采取aB,即标记为负类. 对于阈值γL,可以根据表2的代价矩阵进行计算. 表2 二支分类代价矩阵 则采取aP,aN两种行动下的期望损失可分别表示为: (9) 根据贝叶斯风险最小化原则: (P1)若RL(aP|x)≤RL(aN|x)成立,则x∈POSL(X); (N1)若RL(aN|x)≤RL(aP|x)成立,则x∈NEGL(X). 结合决策规则(P1)-(N1),可以得到γL的计算公式: (10) 基于上述讨论,结合第3节基于Wrapper特征选择的粒化方法,本文提出一种wrapper特征选择下的序贯三支分类方法,其具体实现步骤如算法4所示. 算法 4.Wrapper特征选择下的序贯三支分类方法 输出:分类结果 //基于Wrapper框架构造多层次粒结构 //训练多粒度分类器,计算分类阈值 2.for1≤i≤L 2.1.Si=(U,Gi∪D) 2.2.ψi′=train(ψ,Si) 2.3.i=i+1 3. (αi,βi)=threshold(Mi),1≤i≤L-1,byEq(6),(7) γL=threshold(ML),byEq(10) //序贯三支分类方法 4.U1=U′POS=∅NEG=∅BND=∅i=1 5.while1≤i≤L-1 5.1.foreachx∈Uido 5.1.1.POSi={x∈Ui|ψi′(x)≥αi} 5.1.2.BNDi={x∈Ui|βi<ψi′(x)<αi} 5.1.3.NEGi={x∈Ui|ψi′(x)≤βi} 5.2.POS=POS∪POSi 5.3.BND=BNDi 5.4.NEG=NEG∪NEGi 5.5.Ui+1=BND 5.6.ifUi+1=∅ 5.6.1.returnPOS,NEG;break 5.7.elsei=i+1 6.endwhile 7.ifi=L 7.3.POS=POS∪POSL 7.4.NEG=NEG∪NEGL 8.endif 9.returnPOS,NEG 为了验证本文所提出方法的有效性,表3选取了5个经典的UCI数据集进行实验验证.实验运行环境为Windows 10,运行实验的处理器为Intel i5-8250U,1.6GHz CPU,内存为8G,编程语言为Python 3.7.在本节中,首先介绍数据集的一些基本信息,评价指标,参数和实验的设计;然后对各算法的分类质量进行对比分析;最后对分类的成本进行评估. 表3 数据集描述 本文主要评估评分类质量和分类成本两个方面.在分类质量方面,选用F1值和精度来对方法进行评估. 关于序贯三支分类方法中的参数设置,本文以三层粒结构为例进行对比试验.每层添加属性数目为(|Cr|/2,|Cr|/4,|Cr|/4),其分类代价矩阵设置如表4所示.其中λBP和λBN由延迟成本和信息获取成本两部分构成.进一步地,通过式(6),式(7)和式(10),可以计算得出每层的分类阈值.为了方便起见,我们设置遗传算法参数为:种群数50,交叉率0.9,变异率0.3,迭代次数的停止条件为10次.因为遗传算法具有一定的随机性,所以本文重复运行5次计算平均值.此外,我们假定表3中各数据集属性的测试代价相同.关于WS3WC中分类器ψ的选择,本文以逻辑回归(LOG)和支持向量机(SVM)为例来进行试验. 表4 各粒层分类代价矩阵 为了进一步说明本文方法的有效性,我们选择静态分类器和TS3WC作为基准算法,设计了两组对比实验,具体如表5所示.其中静态分类器是指静态二支分类器; TS3WC引入了序贯三支决策的思想,对样本进行差异化分类,但在粒化过程中不对属性进行约简和排序. 表5 实验设计 表6、表7给出了各方法在每个数据集下的F1值和精度值,以及在5个数据集下的平均F1值和平均精度值.从表6-表7可以看出,3种方法在不同数据集上的分类质量各有高低.当选取LOG分类器时,WS3WC-LOG的表现要略好一些.当选取SVM分类器时,静态分类的表现更好.通过观察3种方法在5个UCI数据集下的平均F1值和平均精度值可以看出:WS3WC和静态分类器的平均F1值和平均精度相差不大,但都优于TS3WC. 表6 算法在各数据集下的的F1值 表7 算法在各数据集下的精度 综上所述,WS3WC与静态分类器在分类质量上差距不大,能够保持较好的分类质量,TS3WC的分类质量要略低于静态分类器和WS3WC.这说明WS3WC能够保持较好分类质量的主要原因在于其粒化方法的优势,将Wrapper特征选择框架引入粒化过程是合理的. 图4(a)-图4(e)给出了各算法在5个数据集上的分类成本,其中分类成本由误分成本,延迟成本和信息处理成本3部分构成.图4(f)给出了各算法在所有数据集上的平均分类成本.为了方便比较,本文将静态分类器的平均分类成本设置为1.从图4中可以看出,相较于静态分类器,WS3WC的分类成本在各个数据集上均有大幅度的下降;TS3WC的分类成本在4个数据集上有较大幅度的降低;同时WS3WC与TS3WC的平均分类成本明显减少,这充分说明了引入序贯三支决策思想可以有效降低静态分类器的分类成本.与此同时,我们注意到粒化方法对分类成本也有极其重要的影响.在Wdbc和Dermatology数据集上, TS3WC的分类成本明显比WS3WC升高;在Shop数据集上,TS3WC的分类成本甚至超过了静态分类器;只有在Ionosphere和Sports数据集上TS3WC和WS3WC的分类成本比较相近;此外,WS3WC的平均分类成本低于TS3WC.通过上述分析可以看出:在粒化过程中考虑冗余属性和属性添加顺序是十分必要的,本文提出的粒化方法能够有效的降低分类成本. 图4 算法在各数据集上的分类成本与平均分类成本 如何降低静态分类器的分类成本,以便更好地解决代价敏感分类问题是本文的研究动机和最终目标.本文将序贯三支决策的思想引入分类过程中,对样本进行差异化分类;同时利用Wrapper特征选择框架消除粒化过程中的冗余属性并且确定属性的添加顺序,提出了一种Wrapper特征选择下的序贯三支分类方法.实验表明,WS3WC不仅保持了良好的分类质量,而且能够大幅降低分类成本. 本文提出的WS3WC方法只是一个基本框架,还有许多问题值得深入研究.三支决策理论在处理多类问题时具有一定的局限性,因此如何解决多分类问题是未来研究方向之一.此外,本文主要关注应用过程中的分类成本,忽略了训练成本,如何将二者综合考虑也是值得进一步研究的问题.
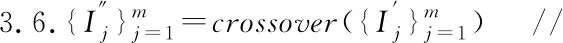
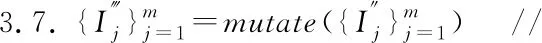
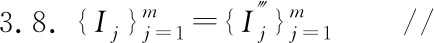
3.2 属性排序
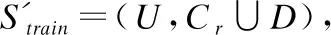
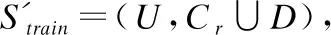

3.3 多层次粒结构
4 序贯三支分类方法
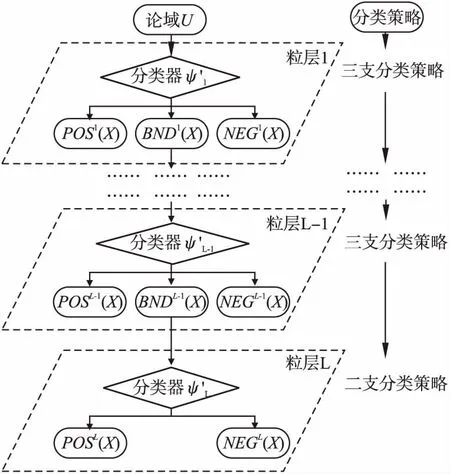
4.1 动态分类策略


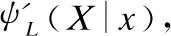

4.2 Wrapper特征选择下的序贯三支分类方法
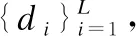
5 实验分析
5.1 评估指标的选择
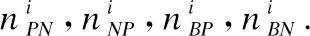
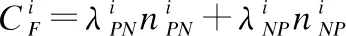

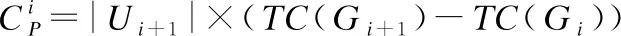
5.2 参数设置和实验设计


5.3 分类质量评估
5.4 分类成本评估

5 结 论

