融合用户特征的微博信息情感演化模型

曹春萍，李 丽

(上海理工大学 光电信息与计算机工程学院，上海 200093)

1 引 言

在信息爆炸的时代，社交网络成为信息传播的主要渠道，微博因其具有便捷性、互动性和快速性等特点，吸引了众多网民的参与微博在容纳公众观点的同时，也激发了公众传播信息的欲望，但同时容易造成一系列负面情绪的传播，形成社会不稳定情绪的蔓延，危及着社会的安全与稳定.因此，如何建立微博网络的信息传播模型，成为非常值得关注的问题.

2 相关研究

基于微博的信息传播模型主要有两类：一类是影响力传播模型[1]，另一类是传染病传播模型[2].影响力传播模型认为网络中的节点只存在激活和非激活两种状态，这不能够完整地体现出微博网络中用户的状态;在传染病模型中，SI模型(Susceptible-Infected model)和SIS模型(Susceptible-Infected-Susceptible model)将网络节点分为未知情者(Susceptible)和传播者(Infected)两种状态，SI模型假设传播者始终处于传播状态，SIS 模型认为传播者可以重新转变为未知情状态.相较于SI模型和SIS模型，SIR模型[3](Susceptible-Infected-Recovered model)引入免疫者(Recovered)状态，认为信息传播过程中传播者最终转变为免疫状态，这更加符合社交网络传播规律.因此，本文采用传染病SIR模型研究微博网络信息的传播.

2.1 SIR模型

经典SIR传播模型是基于微博网络结构并且根据传播规则而得到信息的传播过程.在SIR传播模型中，使用G=(V，E)表示微博网络，其中V={V1，V2，…，Vn}是微博用户的集合，边(u，v)∈E表示用户u和v的关注关系，并且通过3类节点来表示微博网络中不同类型的用户：1)未知情者(Susceptible，S)为没有接受过消息的节点，表示不知道消息的用户;2)传播者(Infected，I)为消息传播节点，表示知道消息并且具有传播能力的用户;3)免疫者(Recovered，R)为接受消息但不再传播的节点，对应知道消息但已失去传播能力的用户.假设社交网络有M个节点，每个节点就代表一个可以传播信息的用户，S(t)、I(t)和R(t)分别代表t时刻内未知情者、传播者和免疫者的数量，即S(t)+I(t)+R(t)=M.因此在SIR传播模型中，假设初始t0时刻，未知情者、传播者和免疫者的数量分别为S(0)、I(0)和R(0)，随后在t时刻内，未知情者S通过接触传播者I后以固定的概率α成为传播者I，传播者I在传播信息后以固定的概率β转变为免疫者R，直至S(t)、I(t)和R(t)数量不再变化，最后结束整个传播过程.根据上述传播规则，构建SIR传播模型如式(1)所示：

(1)

SIR传播模型节点之间传播信息的过程如图1所示.

图1 SIR模型节点状态变化

2.2 相关工作

微博网络中复杂的因素影响着信息传播，不仅包括社会加强效应、兴趣衰减效应和遗忘机制等社会因素，同时还有用户间亲密度、用户影响力等个体因素，考虑到简单的SIR模型不能完整地体现出微博网络中信息传播过程和微博用户的各种状态，因此众多学者考虑不同的传播影响因素，在SIR模型的基础上建立符合微博网络的信息传播模型[4].

Zhao等人[5]考虑节点度和社交网络传播规律，提出了一种基于SEIR的社交网络舆情传播模型.王超等人[6]认为用户由于接受到各式各样的信息导致对某些信息遗忘和失去兴趣，因此将遗忘机制引入SIR模型之中.Ma等人[7]在传SIR模型的基础上，通过增加正向和负向的“双向社会加强效应”的影响改进其中的传染率，动态的研究了处于不同条件下的未知者对于舆论传播的影响.Sun等人[8]结合用户和行为因素，建立了新的社交网络舆情传播模型.张永等人[9]通过定义3个概率函数，并且设置部分微博用户为假免疫状态，得到了更加符合社交网络信息传播特点的SDIR模型.这些研究考虑用户属性及社交效应影响来构建信息传播模型，但却忽略了情感在社交网络中上的传播分析.情感作为信息的另一种表达，往往是与实体信息相关联的，同样随着时间的推移发生演化，把握信息情感倾向对控制舆情起着重要作用.现有的一些研究中，如Zhao等人[10]使用SIR模型对情感传播进行建模;Wang等人[11]引入了某一情绪在用户中转发比例作为传播概率的权重，建立了ESIS模型，利用人工网络和社交网络模拟了信息传播的过程.徐沛东等人[12]基于SIR舆情传播模型并且结合情感网络图论，提出了情感网络传播模型.但是这些对于节点间情感演化的研究均未考虑到社交网络节点之间的差异性，因而与实际的信息情感传播过程存在较大偏差.

针对上述问题，本文在SIR信息传播模型的基础上，将微博用户划分为未知情状态、负面情绪传播状态、正面情绪传播状态和免疫状态这4种状态，基于未知情用户邻居节点中不同影响力的负面情绪传播用户、正面情绪传播用户和当前舆情信息流行度的权重影响，重现定义未知情用户的传播概率;再根据传播用户的影响力和传播时间，重新定义传播用户的遗忘概率，从而建立了SNPR(Susceptible-Negative-Positive-Recovered)情感传播模型，模型中用户传播概率和遗忘概率的非一致性体现了社交网络节点之间的差异性，更好地描述了信息情感在微博网络中的传播过程.

本文的结构安排如下，第2节介绍了近几年研究人员所提出信息传播模型的优缺点，并结合用户属性以及遗忘机制提出SNPR情感传播模型;第3节详细介绍了提出的SNPR情感传播 模型;第4节进行实验，对研究结果进行分析;第5节总结了本文的主要工作和不足之处.

3 SNPR情感传播模型

为研究信息情感在微博上的演化过程，本文在微博信息传播特征以及网络结构的基础上，建立SNPR情感传播模型，分析微博用户在多种影响因素作用下参与信息讨论和表达情绪的概率.

该模型过程如下：

1)依据微博用户之间的关注关系构建微博网络，定义用户状态.

2)依据信息传播机制定义传播规则.

3)结合传播规则和微博网络，改进传播概率和遗忘概率进行信息情感传播.

4)整个传播过程持续至微博网络用户状态不再变化.

3.1 微博网络

微博网络是由“关注者”和“被关注者”以及他们之间关系构成的，如果将每一个微博用户视作节点，则网络中的边表示用户之间的关注关系.本文使用G=(V，E)表示微博网络，其中V={V1，V2，…，Vn}是微博用户的集合，边(u，v)∈E表示微博用户u和v的关注关系，依据关注关系建立邻接矩阵，如式(2)所示.

(2)

其中矩阵元素满足：

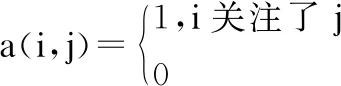
(3)

本文把微博用户划分为4种状态，分别为：未知情状态用户(Susceptible，S)，指不知道舆情信息的用户;负面情绪传播状态用户(Negative，N)，指在微博上发布辱骂、恐怖等具有负面倾向信息的用户;正面情绪传播状态用户(Positive，P)，指在微博上发布中性或积极倾向信息的用户;免疫状态用户(Recovered，R)，R是指发布舆情信息后不再具有传播能力的用户.

3.2 传播规则

在微博网络的信息传播中，如果某一用户没有接触过相关舆情信息，那么受到邻居节点发表言论以及当前舆情信息受关注程度的影响，该用户就有可能变为传播信息的人，其中信息情感可能是负面，可能是正面，这种概率往往与未知情用户邻居节点中传播用户的个体影响力、传播者发布言论的情感以及舆情流行度是有直接关系的.此外，如果某一用户发布言论后，基于用户影响力和遗忘机制，该用户能否继续维持负面情绪传播状态或者正面情绪传播状态的概率也因人而异.本文定义如下传播规则：

a)未知情用户S受到邻居节点中负面情绪传播状态用户N和舆情信息流行度的影响，未知情S将以α1的概率转换成负面情绪传播状态用户N;

b)未知情用户S受到邻居节点中正面情绪传播状态用户P和舆情信息流行度的影响，未知情S将以α2的概率转换成正面情绪传播状态用户P;

c)传播用户在海量的信息轰炸下，可能会遗忘或对该舆情信息失去兴趣，因此，本文假定微博用户在对舆情信息传播一段时间后，由于遗忘效应及兴趣衰减效应，负面情绪传播状态用户和正面情绪传播状态用户将转换为免疫状态，即负面情绪传播状态用户和正面情绪传播状态用户将以遗忘概率β转换为免疫状态用户R.根据上述规则，传播过程如图 2所示.

图2 SNPR传播模型节点状态变化

3.3 传播过程计算

SNPR情感传播模型中存在两个重要概率，即传播概率和遗忘概率，传播概率大于传播概率阈值λa时，未知情状态用户S将会转换为负面情绪传播状态用户N或者正面情绪传播状态用户P，当遗忘概率大于遗忘概率阈值λb时，传播用户N或者P转化为免疫状态用户R.下文将说明如何计算传播概率和遗忘概率.

3.3.1 传播概率

考虑到微博舆情的热度和微博网络的社交性，未知情用户受到邻居节点与权威用户的影响，然后以一定的概率成为负面情绪传播状态N或者是正面情绪传播状态用户P.然而不同的传播者因为影响力不同，所以发表的言论往往对未知情的用户产生不同的作用[13].因此，本文在基础传播概率的基础上，考虑传播用户影响力、信息情感值以及舆情流行度3个影响因素，将邻居传播节点的影响力和发表言论的情感相结合作为传播用户情感影响力，综合传播用户情感影响力和舆情流行度作为传播概率的权重，重新定义未知情用户的传播概率.

用户影响力In(i)：本文中采用PageRank算法[14]计算微博用户的影响力.PageRank 算法基于网页间相互关联的复杂程度来实现网页重要性的排序.在微博中，微博用户可以认为是网页中的链接，其关注的用户类似网页被链接.PageRank算法计算过程如下：首先为所有用户设置相同的影响力值，即In(i)=1;然后按照每个用户关注的人数将影响力值平均分配;最终依据式(4)重新计算用户新的影响力值In(i).为避免指标之间的量纲影响，需对数据进行标准化处理，记微博用户所拥有粉丝数为Fans(i)，根据式(5)对In(i)重新计算，主要算法如图3所示.

(4)

(5)

其中d为0～1之间的一个阻尼系数，实验验证d取值为0.85，算法效果是最好的.Follower(i)是用户粉丝信息集合，Followee(i)是用户关注者数量.

图3 计算用户影响力

用户情感状态emotion(i)：微博用户发布相关言论，文本信息就会产生相应情感，因而需要对文本信息进行处理.本文基于情感词典对微博内容计算情感分值[15].一条微博中往往由多个词组成，首先检测情感词、程度副词和否定词否定词，再对比情感词典、程度副词词典和否定词词典，最后计算出微博文本的情感值.在该算法中，每条微博用Item1、Item2、…、Itemn表示，首先对文本内容分句和分词，得到以下集合：

Itemi=[[Word11，…，Word1n1]，…，[Wordk1，…，Wordknk]]

其中k为Itemi分句后的总句数，nk为每一句的分词个数;接着遍历分词后的语句，对比词典，找出情感词前相应的程度副词和否定词，计算出每个情感词的权值集合{w1，w2，…，wn}，其中n为情感词的个数;最后对比情感词典，得到每个情感词的分值{e1，e2，…，en}，根据式(6)计算出每一条微博的情感值Ei，主要算法如图4所示.

本文最终依据式(7)得到微博用户情感状态emotion(i)，1代表正面情感用户，-1代表负面情感用户，0表示用户未发布任何信息.

(6)

(7)

算法：计算博文信息情感值

图4 计算信息情感值

舆情信息流行度Popularity(t)：即当前用户对该舆情事件的重视程度.参与舆情信息传播的用户越多，说明舆情越受欢迎，未知情用户进行舆情传播的概率也会增大.越受到用户关注.避免舆情参与人数数量过多，本文依据式(8)对舆情参与人数Peo(t)进行处理，其中Peo(t)表示t时刻参与舆情讨论的人数，用P(t)+N(t)+R(t)表示.

(8)

本文采用信息熵加权法来规避传统加权方法的缺陷[16].信息熵加权法的计算过程如式(9)-式(10)所示.首先根据式(9)计算每个属性的熵值，接着依据式(10)分别计算影响因素的权重，使用 ωi来表示.

(9)

(10)

其中，Hi代表第i个属性的熵，rij代表第j个节点的第i个属性的值.因为本方法有用户影响力属性和舆情信息流行度性，所以 i 取值为 1 和 2，因此ω1是用户影响力属性的权重，ω2是信息流行度的权重.

根据PageRank算法和情感分析算法得到传播用户情感影响力，再结合舆情信息流行度，分别作为未知情用户转换为N和P概率的权重，因此未知情S转换为N和P的概率分别如式(11)和式(12)所示，其中Spreader(i)为微博用户i关注人中是传播用户的集合.

(11)

(12)

3.3.2 遗忘概率

当N和P用户参与舆情信息传播具有传播能力，由于遗忘机制及兴趣衰减效应[17]，用户逐渐不再具有传播作用，进而转换为免疫用户.因此本文根据Ebbinghaus遗忘曲线，采用指数形式的遗忘函数作为传播者转换为免疫者的遗忘概率，具体如下：

(13)

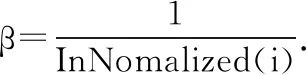
3.3.3 SNPR模型动力学方程

根据上述改进后的SIR模型以及传播概率、遗忘概率，将SNPR模型构建如式(14)所示.

(14)

其中，S(t)、P(t)、N(t)和R(t)分别代表用户在未知情状态、负面情绪传播状态、正面情绪传播状态和免疫状态下t时刻的数量，α1(i)、α2(i)和δi(t)分别表示未知情用户转换为负面情绪传播用户的概率、未知情用户成为为正面情绪传播用户的概率、传播用户成为免疫用户的概率.假设微博网络中的全部用户数量为M，那么在任意时刻，S(t)+P(t)+N(t)+R(t)=M.

4 实验及结果分析

根据上述社交网络信息情感传播的基本特征，使用Python运行环境，基于新浪微博网络对SNPR情感传播模型进行了仿真实验.首先利用微博网络进行实验首先探讨模型参数对模型准确率的影响，在微博网络中，模型目标是预测舆情发展趋势(即参与舆情的用户数).其次，为验证模型各个模块对信息情感传播过程的影响，本文从以情感与实体信息间的关联性以及社交网络节点间的差异性两个方面设置消去实验验证本文所提模型的有效性.最后通过本文提出的模型模拟舆情情感演化趋势，并且与ESIS和EIC模型[18]进行比较，验证本模型的准确性和精确性.

4.1 实验数据

新浪微博实验数据集来源于传播数据挖掘竞赛中的“昆山反杀案”，在此案件中，事件当事人刘海龙因交通事故与行人于海明产生争论，之后刘海龙用砍刀攻击于海明时脱手，被于海明反击砍杀致死，事件发生后，引起了大众的热议.首先对数据集进行预处理和清洗，经过数据清洗后，有效数据为308055条博文记录，共252273名微博用户，最后利用了微博平台的API来获取这些用户之间的关注关系，生成微博网络.

4.2 实验过程

实验第1步是根据情感分析算法将用户发布的博文内容转化为用户对此舆情事件的情感值，其中1表示用户发布的内容是中性或积极的，-1表示用户发表的内容是具有负面倾向的.第2步根据微博用户之间的关注关系，构建有向图G，即根据关注关系构建邻接矩阵.第3步依据PageRank算法计算每个微博用户的影响力值.第4步选取舆情事件发生5小时内用户数量以及用户对应的情感状态作为模型初始数据，并根据式(14)进行传播模拟演化.

4.3 实验结果与分析

为了验证实验模型在微博信息情感演化的效果，本文设置了多个对比实验，从多个角度验证模型的有效性.

1)使用不同实验参数进行对比

实验过程中设置α=0.5，同时存在两个实验参数：传播概率阈值λa和遗忘概率阈值λb.传播概率阈值λa表示未知情用户传播概率α1(i)或者α2(i)大于λa，即未知情S转变为负面情绪N或者正面情绪P，遗忘概率阈值λb表示微博用户遗忘概率大于λb，即传播用户状态用户N或者P转化为免疫状态用户R.本实验采用控制参数法，首先固定其中一个参数，再调试另外一个参数，设置λa在区间[0.01，0.03]之间，设置λb在区间[0.2，0.3]之间，最后计算模型的准确率Accuracy，如公式(15)所示.

(15)

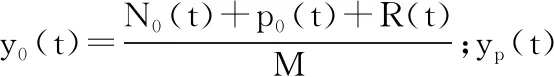
同时，为了减小实验误差，本文将每次实验重复实现50次，并将50次计算得到的准确率求和取平均，得到图5 所示结果.其中，选取不同λa值和λb值，对比实验结果如图6(a-d)所示.

图5 传播概率阈值、遗忘概率阈值和准确率的关系图

从图5中可知，当λa为0.02，λb为0.25时，SNPR模型达到最高的准确率91.5%，即该参数下的模型性能是最佳的.图6展示了不同实验参数下本模型与真实数据拟合结果，当传播概率阈值增大时，传播用户人数减少，进而导致传播趋势与真实数据相比，有明显下降;当遗忘概率阈值增大时，传播用户起到传播作用的时间更久，因而导致模型传播趋势比真实数据更快，早于真实数据到达峰值，模型曲线与真实结果相差增大.

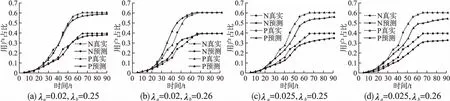
图6 不同参数实验结果图

2)验证不同模块对模型的影响

社交网络中不同影响力节点的不同情绪对信息传播产生不同的作用，为研究情感与实体信息间的关联以及微博用户影响力对信息情感传播过程的影响，本文从以情感与实体信息间的关联性以及社交网络节点间的差异性两个方面设置消去实验验证本文所提模型的有效性.

(1)情感与实体信息间的关联性

为验证实体信息情感对信息情感传播的影响，计算传播概率α(i)不考虑用户情感状态，仅考虑用户影响力，实验设置S以α(i)的概率转变为传播用户I，传播用户I以δi(t)的概率转变为R.实验结果与真实数据进行对比，如图7所示.

(2)社交网络节点间的差异性

为验证微博用户自身影响力对舆情信息情感演化的作用，传播概率α1(i)和α2(i)计算时不考虑用户自身影响力，仅考虑用户情感状态，实验设置未知用情状态用户S以概率α1(i)和α2(i)转换为N或者P，传播状态用户N或者P以固定的概率λb转换为R.实验结果与真实数据进行对比，如图8所示.

从图7和图8可以看出，实验过程中不考虑情感与实体信息间的关联，无法依据文本情感体现舆情信息情感的演化趋势，模型实验拟合效果在精准性上有了一定的降低;实验过程中不考虑社交网络节点间的差异性，模型为理想状态下的传播模型，负面和正面情绪传播用户在初始阶段用户数量大，增长趋势相较于真实数据更快，与真实数据差异较大.由图7和图8可以看出，融合信息情感和社交网络节点影响力这两个特征的模型精准性有了一定的提高，从而使情感演化趋势拟合效果更优.

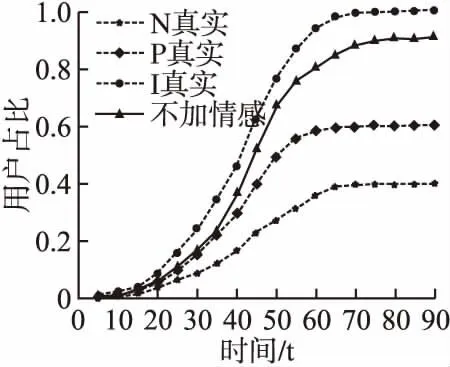
图7 消除信息情感实验结果对比

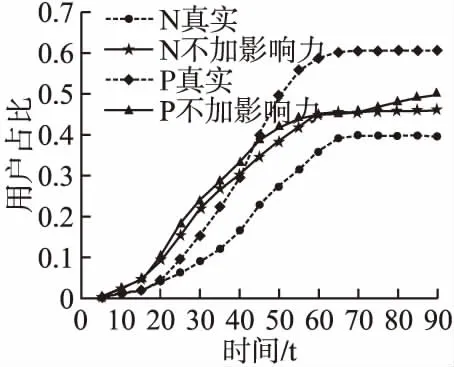
图8 消除用户差异性实验结果对比

3)本文模型与其他模型的对比

为客观的衡量模型性能，选取ESIS模型、EIC模型与SNPR模型进行对比实验.由于这些模型有不同的基础条件，因此需要将它们调整到相同的基准：

(1)ESIS模型将情感分类为细粒度的类，将某一情绪在用户中的转发比例作为权重.在此基础上，我们将情感在ESIS模型分为两种类型，其中无情感和快乐被认为是正面的，愤怒、悲伤、恐惧和厌恶都被认为是负面的.

(2)EIC模型中，边的权值表示用户之间的影响程度，其中情感值中立和积极认为是正面的，消极认为是负面的.

模型参数分别设置为α=0.5，λa=0.2，λb=0.25，本文所提出的模型与ESIS、EIC模型及实际负面情绪和正面情绪演化的拟合实验结果如图9和图10所示.

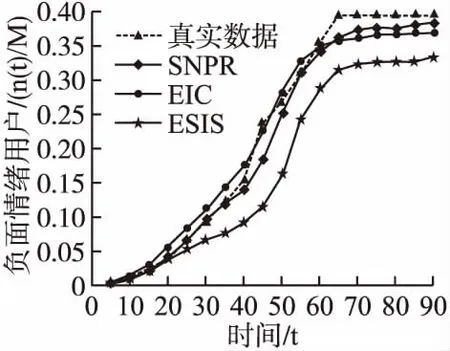
图9 负面情绪演化结果

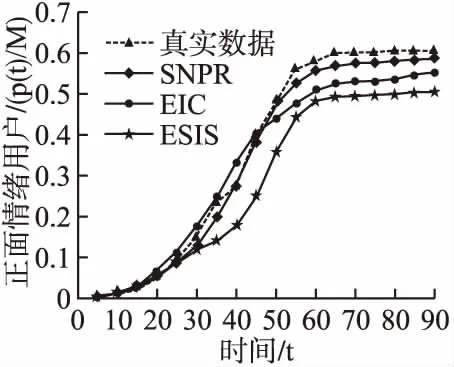
图10 正面情绪演化结果

从图9和图10可以看出，“昆山反杀案”事件在初始阶段的负面情绪用户和正面情绪用户缓慢增长，随着该事件受到关注后，传播趋势增长开始加快，但是初始阶段负面情绪用户数量少于正面情绪用户数量，因此舆情事件整体以正面情绪传播为主导，随着时间的不断增长，正面情绪传播和负面情绪传播趋势以较为缓慢的速度逐渐下降，说明微博用户逐渐对该舆情事件失去兴趣，慢慢对其他未知情者不起传播作用.本文所提模型较好地模拟了舆情事件的情感演化趋势，ESIS和EIC模型初始阶段与和真实数据虽具有一致的发展趋势，但EIC模型传播趋势高于实际数据，ESIS模型传播趋势明显低于实际数据，后期与真实数据的差距越来越大.

此外，为客观衡量模型的准确性，选择均方根误差(RMSE)、平均绝对百分误差(SSE)和决定系数(R2)作为评价指标，计算公式分别如式(16)-式(18)所示.当RMSE和SSE越小时，表明模型拟合数据与真实数据的误差越小，模型精确性越高，同样的R2值越接近于1，表示偏离真实值的程度越小，精度越高，模型也越有效.

(16)

(17)

(18)

其中，T是整个传播过程所需总时间，〈y〉是变量y的平均值，yo(t)是t时刻y的真实值，yp(t)是t时刻变量y的预测值.

根据公式(16)-式(18)，分别计算不同模型的RMSE、SSE和R2，如表1和表2所示.

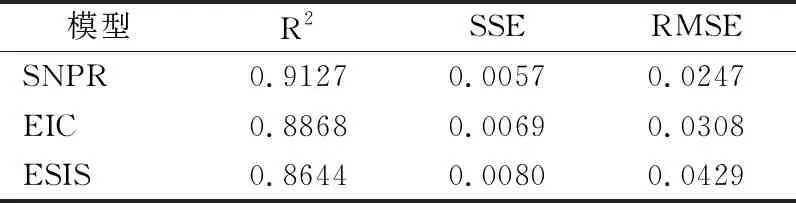
表1 负面情绪演化不同模型比较

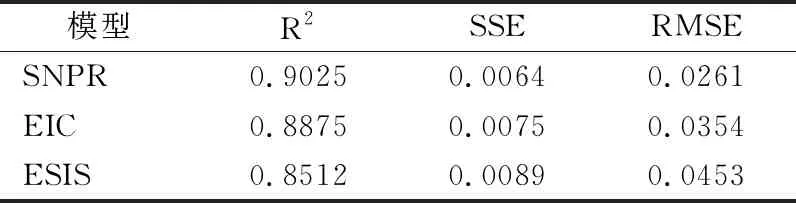
表2 正面情绪演化不同模型比较

本文所提出的模型相较于EIC和ESIS模型，与微博网络中的情感演化趋势更为拟合.相较于ESIS和EIC模型并未考虑遗忘机制和用户情感传播影响力对微博信息情感传播的作用，本模型综合考虑了微博信息情感演化的影响因素，使得模型准确率和精确度均有相应提高，验证了本文模型在微博信息情感演化具有较好效果

5 结束语

针对微博信息传播中情感演化的问题，本文基于信息传播机制，综合考虑信息传播的多个影响因素，在已有的SIR 信息传播模型进行改进，融合情感影响力和遗忘机制建立SNPR情感传播模型，说明信息情感在微博的演化过程.本文选取“昆山反杀案”微博舆情事件进行实验验证，确定本模型在真实网络上预测的准确性，结果表明，本文所提模型与ESIS和EIC模型相比，准确性有了明显的提高.但是，本文研究并未考虑其他非关注用户是否对用户产生影响，同时用于情感分类的算法质量还有待提高，故如何进一步提高模型的准确性是本文未来研究的主要方向.